中值定理、洛必达、函数单调性、极值、最值,凹凸性的应用

2016考研数学：三个微分中值定理每年考研数学必有一道证明题，分值在10分左右，其中百分之九十涉及到的是微分中值定理及其应用。

而微分中值定理及其应用最难的就是三个微分中值定理：罗尔定理、拉格朗日中值定理、柯西中值定理。

它们是考研数学的重难点，现分别从涉及的知识点、考查方式、方法选择、真题链接等四个方面进行分析。

一、涉及的知识点及考查形式可涉及微分中值定理及其应用的知识点有，微分中值定理，洛必达法则，函数单调性的判别，函数的极值，函数图形的凹凸性、拐点及渐近线，函数图形的描绘，函数的最大值与最小值，弧微分(数一、数二要求)，曲率的概念(数一、数二要求)，曲率圆与曲率半径(数一、数二要求)。

微分中值定理以间接考查或与其他知识点综合出题的比重很大，也可以直接出题，所以考查形式有多种。

如利用导数的几何意义考查函数的特性，讨论导数零点存在性或方程根个数问题，不等式的证明，证明含中值的等式，求极限等。

二、方法选择题目考查微分中值定理，那么选择哪一中值定理成为解题的关键。

针对题目的特点，可根据如下情况选择对应的微分中值定理：如果结论不包含端点，优先考虑罗尔定理；如果结论中包含端点，则考虑拉格朗日中值定理或柯西定理。

那么选择拉式还是柯西定理，需要对结论做进一步的处理，化为定理的标准形式。

如第一个标准，左边是只含端点，右边只含中值；第二个标准，左边进一步处理，分子分母减号，一侧只含右端点，一侧只含左端点。

整理后，如果分母是端点相减，则选择拉格朗日定理；否则，选择柯西定理。

三、求解步骤及历年真题解析涉及到微分中值定理，一般首先要找辅导函数。

针对拉式中值定理和柯西定理，经过对要证明的结论化为标准形式，可直接得出辅助函数。

而罗尔定理，需要把结论化为微分方程的一般形式，使用积分因子法可找到。

有了辅助函数，根据中值定理，列出定理对应的三个条件，得出结论。

四、小结三个微分中值定理(条件与结论)的理解及其区别是复习的要点，而方法的选择是解题的关键。

第四章 微分中值定理和导数的应用本章知识◆ 微分中值定理 ◆ 洛必达法则◆ 函数单调性的判定 ◆ 函数的极值及其求法 ◆ 函数的最值及其应用 ◆ 曲线的凹凸性和拐点 ◆ 曲线的渐近线◆ 导数在经济分析中的应用本章重点：拉格朗日中值定理，洛必达法则，函数单调性的判定，函数极值、最值的求法和实际应用本章难点：函数最值的应用，弹性函数 4.1微分中值定理 4.1.1罗尔定理定理（罗尔（Rolle ）中值定理）：若 f (x)满足： （1）在[a, b]上连续， （2）在(a, b)内可导， （3）f (a) = f (b)，则至少存在一点(,)a b ξ∈，使得()0.f ξ'=罗尔中值定理的几何意义两端高度相同的一段连续曲线上，若除端点外它在每一点都有不垂直于x 轴的切线，则在其中必至少有一条切线平行于x 轴.4.1.2拉格朗日(Lagrange)中值定理定理：拉格朗日(Lagrange)中值定理若 f (x)满足： （1）在[a, b]上连续，（2）在(a, b)内可导，则至少存在一点(,)a b ξ∈，使得()()().f b f a f b a ξ-'=-拉格朗日(Lagrange)中值定理的几何意义在曲线弧AB 上，至少存在一点C ，该点的切线平行于AB 。

拉氏公式精确地表达了函数在一个区间上的增量与函数在这区间内某点处的导数之间的关系.'(,),()0,()()x a b f x f x c c ∈==推论：如果对于任意有则为常数()()(,)()()()x a b f x g x f x g x c c ''∈=+/推论：如果对于任意，有=则为常数4.2洛必达法则洛必达法则型型及基本不定式:001.2.4∞∞()(),()(),()0lim .()0x a x x a x f x g x f x g x →→∞→→∞∞∞如果当或时两个函数与都趋于零或都趋于无穷大那么极限称为或型未定式 定理 (洛必达法则)：(),()(1),()();(2)(),()()()0;()(3)lim ();()()()lim lim .()(),.()().x a x a x a f x g x x a f x g x a a f x g x g x f x g x f x f x g x g x x f x g x →→→→'''≠'''='→∞设满足：当时函数及都趋于零在点的某领域内点本身可以除外及都存在且存在或为无穷大那么当时该法则仍然成立当及都趋于无穷大时，该法则仍注1：注2然成立：注意：洛必达法则是求未定式的一种有效方法，与其它求极限方法结合使用，效果更好.()()()()()()()()()()()()x g x f x g x f x g x f x g x f x g x f x g x f x x x x x x x x x x ''''=''=''∞∞''∞∞→→→→→00000lim lim lim 00lim 200lim1续使用洛必达法则，即仍满足定理，则可以继，”型不定式，且函数”或“还是“）若”型不定式”或“必须是“）注意使用洛必达法则是必须4.2.2其他不定式000,,0,1,∞⋅∞∞-∞∞型未定式解法关键:将其它类型未定式化为洛必达法则可解决的类型。

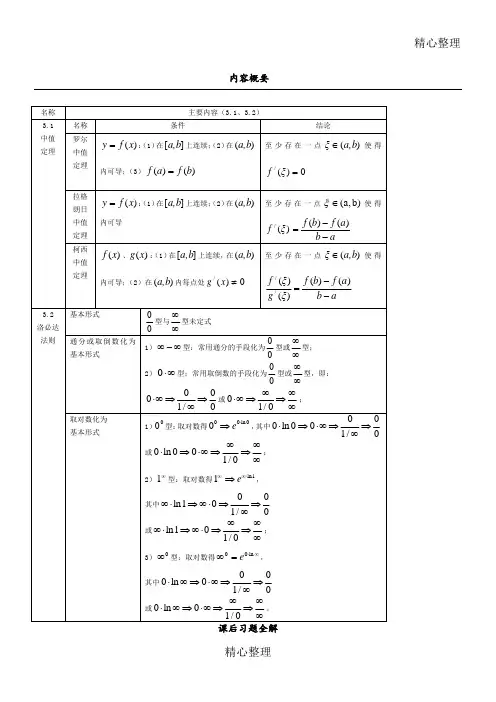
精心整理内容概要习题3-1★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值ξ。

（1）]511[32)(2.,,x x x f ---=；（2）]30[3)(,,x x x f -=。

知识点：罗尔中值定理。

思路：根据罗尔定理的条件和结论，求解方程0)(/=ξf ，得到的根ξ便为所求。

解：)5.即为所（2∴f (f '★2.思路 解∴5(01)12,ξ±∃=，使(1)(0)()10f f f ξ-'=-，验证完毕。

★3.已知函数4)(x x f =在区间]21[,上满足拉格朗日中值定理的条件，试求满足定理的ξ。

解：要使(2)(1)()21f f f ξ-'=-，只要3415ξξ=⇒=(12)ξ,=即为满足定理的ξ。

★★4.试证明对函数r qx px y ++=2应用拉格朗日中值定理时所求得的点ξ总是位于区间的正中间。

证明：不妨设所讨论的区间为][a,b ，则函数r qx px y ++=2在][a,b 上连续，在)(a,b 内可导，从而有()()()f b f a f ξb a-'=-，即a b r qa pa r qb pb q ξ-++-++=+)()(222， 解得2ab ξ+=，结论成立。

★5.函数3)(x x f =与1)(2+=x x g 在区间]21[,上是否满足柯西定理的所有条件？如满足，请求出满足定理的数值ξ。

知识点：柯西中值定理。

思路解，所以满★★★6.存在ξ思路，然后再证明)0(F ()()()0F ξf ξξf ξ''=+=，即()()f ξf ξξ'=-。

注：辅助函数的构造方法一般可通过结论倒推，如：要使()()f x f x x'=-，只要 ∴只要设辅助函数)()(x xf x F =★★7.若函数)(x f 在)(a,b 内具有二阶导函数，且)()()(321x f x f x f ==)(321b x x x a <<<<，证明：在)(31,x x 内至少有一点ξ，使得()0f ξ''=。