4土的应力应变特性
- 格式:doc
- 大小:2.00 MB
- 文档页数:12

一、填空题1.饱和土体上的总应力由土骨架承担的有效应力和由孔隙承担的孔隙水压力组成,土的强度及变形都是由土的有效应力决定的。
2.莱特邓肯屈服准则在常规三轴压缩实验中,当 时它在π平面上的屈服与破坏轨迹趋近于一个圆;当 时,它退化为一个正三角形。
由于在各向等压时,所以K f>27是必要条件,因为静水压力下不会引起材料破坏。
3. 东海风力发电桩基础有8根。
4.通过现场观测与试验研究,目前认为波浪引起的自由场海床土体响应的机制主要取决于海床中孔隙水压力的产生方式。
孔隙水压力产生方式有两种:超孔隙水压力的累积(残余孔隙水压力)、循环变化的振荡孔隙水压力5.目前计算固结沉降的方法有()、()、()及()。
答案:弹性理论法、工程实用法、经验法、数值计算法。
6.根据莫尔—库伦破坏准则,理想状态下剪破面与大主应力面的夹角为()。
答案:45 + /7.土的三种固结状态:欠固结、超固结、正常固结。
8.硬化材料持续受力达到屈服状态后的变化过程:屈服硬化破坏=。
9.相对密实度计算公式ID10.静力贯入试验的贯入速率一般为 2cm/s。
11用一种非常密实的砂土试样进行常规三轴排水压缩试验,围压为 100kPa 和3900kPa,用这两个试验的莫尔圆的包线确定强度参数有什么不同?答:当围压由100kPa 增加到3900kPa 时,内摩擦角会大幅度降低。
12.塑性应力应变关系分为_____理论和_____________理论两种增量(流动)、全量(形变)13.三轴剪切试验依据排水情况不同可分为()、()、()答案:不固结不排水剪、固结不排水剪、固结排水剪。
14.一种土的含水量越大,其内摩擦角越(小)。
15.剑桥模型(MCC)中的5个参数一次是 M VCL中的гλ,以及弹性部分的 K υ。
16.剑桥模型的试验基础是正常固结土和超固结土试样的排水和不排水三轴试验。
17.一般情况下,石英砂的内摩擦角为 29~33二、简答题1.影响土强度的一般物理性质?答:1.颗粒矿物成分 2.粗粒土颗粒的几何性质 3.土的组成颗粒级配 4.土的状态 5.土的结构6.剪切带的存在对土强度的影响。

2-1.什么叫材料的本构关系?在上述的本构关系中,土的强度和应力-应变有什么联系? 答:材料的本构关系是反映材料的力学性质的数学表达式,表现形式一般为应力-应变-强度-时间的关系,也成为本构定律,本构方程。
土的强度是土受力变形发展的一个阶段,即在微小的应力增量作用下,土单元会发生无限大或不可控制的应变增量,它实际上是土的本构关系的一个组成部分。
2-7什么是加工硬化?什么是加工软化?请绘出他们的典型的应力应变关系曲线。
答:加工硬化也称应变硬化,是指材料的应力随应变增加而增加,弹增加速率越来越慢,最后趋于稳定。
加工软化也称应变软化,指材料的应力在开始时随着应变增加而增加,达到一个峰值后,应力随应变增加而下降,最后也趋于稳定。
加工硬化与加工软化的应力应变关系曲线如右图。
2-8什么的是土的压硬性?什么是土的剪胀性?答:土的变形模量随着围压提高而提高的现象,称为土的压硬性。
土的剪胀性指土体在剪切时产生体积膨胀或收缩的特性。
2-9简述土的应力应变关系的特性及其影响因素。
答:土是岩石风化形成的碎散矿物颗粒的集合体,通常是固、液、气三相体。
其应力应变关系十分复杂,主要特性有非线性,弹塑性,剪胀性及各向异性。
主要的影响因素是应力水平,应力路径和应力历史。
2-10定性画出在高围压(MPa 303<σ)和低围压(KPa 1003=σ)下密砂三轴试验的v εεσσ--)(131-应力应变关系曲线。
答:如右图。
横坐标为1ε,竖坐标正半轴为)(31σσ-,竖坐标负半轴为v ε。
2-13粘土和砂土的各向异性是由于什么原因?什么是诱发各向异性?答:粘土和砂土的各向异性是由于其在沉积过程中,长宽比大于1的针、片、棒状颗粒在重力作用下倾向于长边沿水平方向排列而处于稳定的状态。
同时在随后的固结过程中,上覆土体重力产生的竖向应力与水平土压力大小不等,这种不等向固结也造成了土的各向异性。
诱发各向异性是指土颗粒受到一定的应力发生应变后,其空间位置将发生变化,从而造成土的空间结构的改变,这种结构的改变将影响土进一步加载的应力应变关系,并且使之不同于初始加载时的应力应变关系。


土力学第四版习题答案第一章:土的物理性质和分类1. 土的颗粒大小分布曲线如何绘制?- 通过筛分法或沉降法,测量不同粒径的土颗粒所占的比例,然后绘制颗粒大小分布曲线。
2. 如何确定土的密实度?- 通过土的干密度和最大干密度以及最小干密度,计算土的相对密实度。
3. 土的分类标准是什么?- 根据颗粒大小、塑性指数和液限等指标,按照统一土壤分类系统(USCS)进行分类。
第二章:土的力学性质1. 土的应力-应变关系是怎样的?- 土的应力-应变关系是非线性的,通常通过三轴试验或直剪试验获得。
2. 土的强度参数如何确定?- 通过土的三轴压缩试验,确定土的内摩擦角和凝聚力。
3. 土的压缩性如何影响地基沉降?- 土的压缩性越大,地基沉降量越大,反之亦然。
第三章:土的渗透性1. 什么是达西定律?- 达西定律描述了土中水流的速度与水力梯度成正比的关系。
2. 如何计算土的渗透系数?- 通过渗透试验,测量土样在一定水力梯度下的流速,计算渗透系数。
3. 土的渗透性对边坡稳定性有何影响?- 土的渗透性增加可能导致边坡内部水压力增加,降低边坡的稳定性。
第四章:土的剪切强度1. 什么是摩尔圆?- 摩尔圆是一种图解方法,用于表示土的应力状态和剪切强度。
2. 土的剪切强度如何影响基础设计?- 土的剪切强度决定了基础的承载能力,是基础设计的重要参数。
3. 土的剪切强度与哪些因素有关?- 土的剪切强度与土的类型、密实度、含水量等因素有关。
第五章:土的压缩性与固结1. 固结理论的基本原理是什么?- 固结理论描述了土在荷载作用下,孔隙水逐渐排出,土体体积减小的过程。
2. 如何计算土的固结沉降?- 通过固结理论,结合土的压缩性指标和排水条件,计算土的固结沉降量。
3. 固结过程对土工结构有何影响?- 固结过程可能导致土工结构产生不均匀沉降,影响结构的稳定性和使用寿命。
第六章:土的应力路径和强度准则1. 什么是应力路径?- 应力路径是土体在加载过程中应力状态的变化轨迹。

土力学一、介绍土力学是土木工程中的一个重要学科,研究土壤力学和土木工程中土壤的应力、应变和变形等方面的规律。
土力学的研究对象是土壤及其力学性质,通过对土壤的特性和行为的研究,可以预测和控制土壤在工程中的行为,为土木工程的设计和施工提供科学依据。
二、土壤力学的基本概念1. 土壤物理性质土壤的物理性质包括土壤的颗粒组成、容重、孔隙比、相对密度等。
这些性质直接影响土壤的承载力、抗剪强度和渗透性等力学性质,是土壤力学研究的基础。
2. 土壤力学参数土壤力学参数包括土壤的压缩性、内摩擦角、剪切强度参数等。
这些参数描述了土壤在受力作用下的变形和破坏特性,是土壤力学分析和计算的重要依据。
3. 土壤应力状态土壤应力状态是指土壤中的应力分布情况,包括垂直应力、水平应力和剪应力等。
了解土壤的应力状态可以帮助工程师预测土壤的承载力、变形和破坏状态,从而设计出安全可靠的土木工程。
三、土壤力学的应用1. 土壤的承载力分析土壤的承载力是指土壤在承受外力作用下的最大抵抗能力。
工程师通过对土壤的颗粒组成、孔隙结构、内摩擦角等参数的分析,计算得出土壤的承载力,并根据承载力的大小来设计和选择合适的基础结构和土方工程。
2. 土壤的变形特性研究土壤在受力作用下会发生变形,包括压缩变形、剪切变形和液化等。
了解土壤的变形特性可以帮助工程师预测土壤的沉降和位移,并采取相应的补充措施,确保土木工程的安全和稳定。
3. 土壤的抗剪强度分析土壤的抗剪强度是指土壤在剪切作用下的抵抗能力。
通过对土壤的剪切试验和理论分析,工程师可以确定土壤的剪切强度参数,并结合实际工程条件进行抗剪强度的计算和分析,为土木工程的设计和施工提供重要依据。
四、土力学的挑战与发展土力学作为土木工程中的重要学科,正面临着一系列的挑战和发展机遇。
首先,随着城市化进程的加快和人口增长的需求,工程建设规模不断扩大,对土力学的研究和应用提出了新的要求。
其次,随着科技的进步和实验技术的发展,土力学研究手段和方法也将得到加强和完善,从而能够更加准确和全面地研究土壤的力学性质和行为规律。


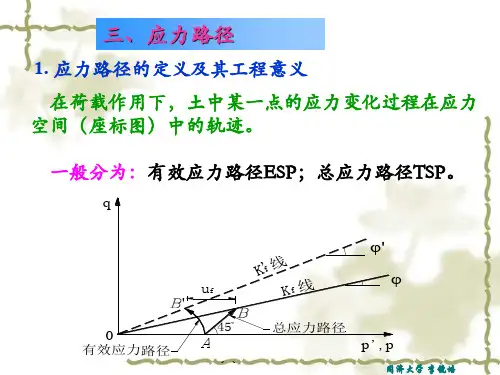


高等土力学期末考试试题汇总.总结高等土力学期末考试试题汇总.总结1、填空:主要影响土的因素应力水平,应力路径,应力历史2、填空:土的主要应力应变特性非线性,弹塑性,剪胀性3、概念:应力历史:包括自然土在过去地质年月中受到固结和地壳运动作用刘翰青一、论述题邓肯-张模型中参数a,b,B各代表什么含义?他们是怎样确定的?答:在邓肯-张模型中,a,b为试验常数。
在常规三轴压缩试验中,式子可写为由于δ2=δ3=0,所以有 =在起始点,有ε1=0, Et=Ei, 则Ei=1/a, 即a代表试验起始变形模量Ei的倒数。
当ε1趋向于﹢∞时,有s1-s3=(s1-s3)ult=1/b则b为极限应力偏差的倒数B为体变应量,在E-B模型中提出,用来代替切线泊松比γt。
其中,B与δ3有关。
a,b,B通常用阅历公式计算确定:二、名词解释次弹性模型:是一种在增量意义上的弹性模型,亦即只有应力增量张量和应变增量张量间存在一一对应的弹性关系,因此,也被称为最小弹性模型。
一般函数关系为dσij = Fij (σmn , dεkl),或dεij= Qij (εmn, dσkl)韩凯1:什么是加工硬化?什么是加工软化?答:加工硬化也称应变硬化,是指材料的应力随应变增加而增加,弹增加速率越来越慢,最终趋于稳定。
加工软化也称应变软化,指材料的应力在开头时随着应变增加而增加,达到一个峰值后,应力随应变增加而下降,最终也趋于稳定。
2说明塑性理论中的屈服准则、流淌规章、加工硬化理论、相适应和不相适应的流淌准则。
答:在多向应力作用下,变形体进入塑性状态并使塑性变形连续进行,各应力重量与材料性能之间必需符合肯定关系时,这种关系称为屈服准则。
屈服准则可以用来推断弹塑性材料被施加一应力增量后是加载还是卸载,或是中性变载,亦即是推断是否发生塑性变形的准则。
流淌规章指塑性应变增量的方向是由应力空间的塑性势面g打算,即在应力空间中,各应力状态点的塑性应变增量方向必需与通过改点的塑性势能面相垂直,亦即=(1)流淌规章用以确定塑性应变增量的方向或塑性应变增量张量的各个重量间的比例关系。
高等土力学主要知识点整理(李广信版)第二章土的本构关系(一)概述材料的本构关系是反映其力学性能的数学表达式,一般为应力-应变时间-强度的关系,也称本构定律、本构方程。
土的强度是土受力变形的一个阶段,即微小应力增量小,发生无限大(或不可控制)应变增量,实际是本构关系一个组成部分,是土受力变形的最后阶段。
第一应力不变量kk z y x I σσσσ=++=1第二应力不变量kk yz xz xy z y z x y x I στττσσσσσσ=---++=2222第三应力不变量22232xyz xz y yz x yz xz xy z y x I τστστστττσσσ---+= 坐标系选择使剪应力为零3211σσσ++=I ,3231212σσσσσσ++=I 3213σσσ=I 球应力张量)(31)(3131321332211σσσσσσσσ++=++==kk m 偏应力张量ii kk ij ij s δσσ31-=,其中=≠=j i j i ii 10δ,克罗内克解第一偏应力不变量01≡=kk s J 第二偏应力不变量()()()[]23123222126121σσσσσσ-+-+-==ji ij s s J 第二偏应力不变量()()()213312321322227131σσσσσσσσσ------==ki jk ij s s s J 1.土的应力应变特性:非线性(应变/加工硬化、应变/加工软化)、剪胀性、弹塑性、各向异性、结构性、流变性(蠕变、应力松弛)。
加工硬化:应力随应变增加而增加,但增加速率越来越慢,最后趋于稳定(正常固结黏土、松砂)加工软化:应力一开始随应变增加而增加,超过一个峰值后,应力随应变增加而减小,最后趋于稳定(超固结黏土、松砂)剪胀性:剪应力引起的体积变化,含剪胀和剪缩土的结构性:由土颗粒空间排列集合、土中各相和颗粒间作用力造成,可明显提高土的强度和刚度。
灵敏度:原状黏性土与重塑土的无侧限抗压强度之比土的蠕变:应力状态不变条件下,应变随时间逐渐增长的现象,随土的塑性、活动性、含水量增加而加剧土的应力松弛:维持应变不变,材料内应力随时间逐渐减小的现象压硬性:土的变形模量(指无侧限,压缩模指完全侧限)随围压而提高的现象。
一、 名词解释1、固结:根据有效应力原理,在外荷载不变的条件下,随着土中超静孔隙水压力的消散,有效应力将增加,土体将被不断压缩,直至达到稳定,这一过程称为~。
单向固结:土体单向受压,孔隙水单向渗流的条件下发生的固结。
2、 固结度:在某一荷载作用下,经过时间t 后土体固结过程完成的程度。
3、 平均固结度:在某一荷载作用下,经过时间t 后所产生的固结变形量与该土层固结完成时最终固结变形量之比称为~。
4、固结系数:反映土的固结特性,孔压消散的快慢,与渗透系数k 成正比,与压缩系数a 成反比,(1)v v wk e C a γ+=⋅5、 加工硬化(应变硬化):正常固结粘土和松砂的应力随应变增加而增加,但增加速率越来越慢,最后趋于稳定。
6、 加工硬化定律(理论):计算一个给定的应力增量引起的塑性应变大小的准则。
7、 加工软化(应变软化):在密砂和超固结土的试验曲线中,应力一般是开始时随应变增加而增加,达到一个峰值后,应力随应变增大而减小,最后趋于稳定。
8、 压硬性:土的变形模量随围压增加而提高的现象。
9、剪胀性:由剪应力引起的体积变化,实质上是由于剪应力引起的土颗粒间相互位置的变化,使其排列发生变化,加大颗粒间的孔隙,从而体积发生了变化。
10、 屈服准则:可以用来弹塑性材料被施加应力增量后是加载还是卸载或是中性变载,即是否发生变形的准则。
屈服准则用几何方法来表示即为屈服面(轨迹)。
11、 流动准则:在塑性理论中,用于确定塑性应变增量的方向或塑性应变增量张量的各个分量间的比例关系的准则,也叫做正交定律。
塑性势面g 与屈服面f 重合(g=f ),称为相适应的~;如果g f ≠,即为不相适应流动规则。
12、 物态边界面:正常固结粘土'p ,'q 和v 三个变量间存在着唯一性关系,所以在 ''p q v --三维空间上形成一个曲面称为~,它是以等压固结线NCL 和临界状态线CSL 为边界的。
1.4 土的应力应变特性1.4.1 土应力应变关系的非线性1.4.2 土的剪胀性1.4.3 土体变形的弹塑性1.4.4 土应力应变的各向异性1.4.5 土的结构性1.4.6 土的流变性1.4.7 影响土应力应变关系的应力条件由于土是岩石风化而成的碎散颗粒的集合体,一般包含有固、液、气三相,在其形成的漫长的地质过程中,受风化、搬运、沉积、固结和地壳运动的影响,其应力应变关系十分复杂,并且与诸多因素有关。
其中主要的应力应变特性是其非线性、剪胀(缩)性和弹塑性。
主要的影响因素是应力水平(Stress level)、应力路径(Stress path)和应力历史(Stress history),亦称3S 影响。
1.4.1 土应力应变关系的非线性由于土由碎散的固体颗粒组成,土宏观的变形主要不是由于颗粒本身变形,而是由于颗粒间位置的变化。
这样在不同应力水平下由相同应力增量而引起的应变增量就不会相同,亦即表现出非线性。
图2‐3‐1 表示土的常规三轴压缩试验的一般结果,其中实线表示密实砂土或超固结粘土,虚线表示松砂或正常固结粘土。
从图(a)可以看到,正常固结粘土和松砂的应力随应变增加而增加,但增加速率越来越慢,最后逼近一渐近线;而在密砂和超固结土的试验曲线中,应力开始随应变增加而增加,达到一个峰值之后,应力随应变增加而下降,最后也趋于稳定。
在塑性理论中,前者称为应变硬化(或加工硬化),后者称为应变软化(或加工软化)。
应变软化过程实际上是一种不稳定过程,有时伴随着应力的局部化——剪切带的产出现,其应力应变曲线对一些影响因素比较敏感。
而且由于其应力应变间不成单值函数关系,所以反映土的应变软化的数学模型一般形式复杂,难以准确反映这种应力应变特点;此外,反映应变软化的数值计算方法也有较大难度。
1.4.2 土的剪胀性由于土是碎散的颗粒集合,在各向等压或等比压缩时,孔隙减少,从而发生较大的体积压缩。
这种体积压缩大部分是不可恢复的,如图2‐3‐2 所示。
在图2‐3‐1(b)中,可以发现,在三轴试验中,对于密砂或强超固结粘土偏差应力σ1-σ3增加引起了轴应变ε1 的增加,但除开始时少量体积压缩(正体应变)外,发生明显的体胀(负体应变)。
由于在常规三轴压缩试验中,平均主应力增量∆p =1/3(σ1−σ3)在加载过程中总是正的,不可能是体积的弹性回弹,因而这种体应变只能是由剪应力引起的,被称为剪胀性(Dilatancy)。
广义的剪胀性指剪切引起的体积变化,包括体胀,也包括体缩。
后者也常被称为“剪缩”。
土的剪胀性实质上是由于剪应力引起土颗粒间相互位置的变化,使其排列发生变化而使颗粒间的孔隙加大(或减小),从而发生了体积变化。
1.4.3 土体变形的弹塑性在加载后卸载到原应力状态时,土一般不会恢复到原来的应变状态。
其中有部分应变是可恢复的,部分应变是不可恢复的塑性应变,并且后者往往占很大比例。
可以表示为:ε=εe+εp(2.3.1)其中εe表示弹性应变,εp表示塑性应变。
图2‐3‐3表示的承德中密砂(一种天然均匀细砂)在σ3= 100kPa的三轴试验结果。
其中单调加载试验曲线用虚线表示;循环加载试验曲线用实线表示。
可见每一次应力循环都有可恢复的弹性应变及不可恢复的塑性应变,亦即永久变形。
对于结构性很强的原状土,如很硬的粘土,可能在一定的应力范围内,它的变形几乎是“弹性”的,只有到一定的应力水平时,亦即达到屈服条件时,才会产生塑性变形。
一般土在加载过程中弹性和塑性变形几乎是同时发生的,没有明显的屈服点,所以亦称为弹塑性材料。
土在应力循环过程中另一个特性是存在滞回圈,在图2‐3‐3 中卸载初期应力应变曲线陡降,减少到一定偏差应力时,卸载曲线变缓,再加载曲线开始陡而随后变缓。
这就形成一滞回圈,越接近破坏应力时,这一现象越明显。
在图2‐3‐3 中另一个值得注意的现象是卸载时试样发生体缩。
由于卸载时平均主应力p 是减少的,这种卸载体缩显然无法用弹性理论解释。
人们认为这主要源于土的剪胀变形的可恢复性和加载引起土结构的变化。
总之,即使是在同一应力路径上的卸载——再加载过程,土的变形也并非是完全弹性的。
但一般情况下,近似认为是弹性变形。
1.4.4 土应力应变的各向异性所谓各向异性是指在不同方向上材料的物理力学性质不同。
由于土在沉积过程中,长宽比大于1 的针、片、棒状颗粒在重力作用下倾向于水平方向排列而处于稳定的状态;另外,在随后的固结过程中,竖向的上覆土体重力产生的竖向应力与水平土压力产生的水平应力大小是不等的,这种不等向固结也会产生土的各向异性。
土的各向异性主要表现为横向各向同性,亦即在水平面各个方向的性质大体上是相同的,而竖向与横向性质不同。
土的各向异性可分为初始各向异性(Inherent anisotropy)和诱发各向异性(Induced anisotropy)。
天然沉积和固结造成的各向异性可归入初始各向异性之列。
在室内重力场中,各种制样过程也会使土试样具有不同程度的初始各向异性。
检验初始各向异性的最简单的试验是等向压缩试验。
在对土样进行等向压缩试验时,经常发现轴向应变小于1/3体应变,即εz=(0.17 ~0.22)εV 。
这表明竖直方向比水平方向的压缩性小。
图2‐3‐4是用自由下落的小玻璃珠制成模拟“土”试样在各向等压试验中的结果。
其中εx=εy= 2.2εz,εz为竖直方向的应变,εv= 5.4εz 。
这种各向异性是由于小玻璃珠在不同方向的排列不同引起的。
图2‐3‐5表示的是砂土的试验结果。
试样是在空气中用撒砂雨的方法制成的立方体三轴试样,用立方体真三轴仪进行的常规三轴压缩试验。
竖直方向大主应力与砂土的沉积面(图中阴影线表示)成夹角θ,θ=90°表示的是常规方法制样试验情况,即大主应力σ1与沉积面垂直。
从图可见不同方向试验的应力应变曲线是不同的。
从图中可见,对于θ=90°和θ=40°的试验可以用一条曲线表示,θ=30°和θ=20°的试验结果也可以用一条曲线表示,而θ=0°用单独一条曲线表示,最上部曲线是用常制样(θ=90°)和常规三轴仪进行的常规三轴试验结果。
在θ=20°和θ=40°的试验中,实测的两个横向应变ε2与ε3是不等的,ε3> ε2 。
所谓诱发各向异性是指土颗粒受到一定的应力发生应变后,将发生空间位置的变化,从而改变了土的空间结构。
这种结构的变化对于土进一步加载的应力应变关系将产生影响,并且不同于初始加载时的应力应变关系。
图2‐3‐6表示的正常固结粘土的一种三轴试验:首先试样被等比固结到τ=(σ1−σ3)/ 2 =14.2kPa 和σ=(σ1+ σ3)/ 2 =90kPa,然后在五个方向施加相同的应力增量,量测相应的应变增量。
可见不同方向应力增量引起的应变增量方向和大小都不同,其中初始不等向固结所引起的各向异性是主要原因。
例如对于沿原应力路径④加载产生的应变路径与原固结的应力路径完全一致,而其他应力路径则不然。
上述例子都是室内制样的情况,原状天然土的各向异性往往更强烈,也比较复杂。
原状土的各向异性常常是其结构性的一个方面的表现。
1.4.5 土的结构性土是由分散的颗粒组成的。
土的强度、渗透性和应力应变关系特性是由这些颗粒的矿物、大小、形状,颗粒间的排列和粒间的作用力决定的。
所谓土的组构(fabric)通常是指颗粒、粒组和孔隙空间的几何排列方式;而土的结构(structure)则更倾向于用来表示土的组成成分、空间排列和粒间作用力的综合特性。
所谓土的结构性就是由于土颗粒的空间排列集合及土中各相间和颗粒间的作用力造成的力学特性。
结构性的强弱表示土的结构对于其力学性质(强度、渗透及变形性质)影响的强烈程度。
由于在实验室和野外土都不可避免地处于地球的重力场中,不可能达到完全随机的排列及颗粒间相互完全独立无联系,如室内制样的方法、程序和环境,在天然情况下土的生成、搬运、沉积、固结及在千万年地质历史中所受到的各种变故等。
因而不管是原状土还是室内重塑土总是表现出不同的或特有的结构性。
一般讲原状土比重塑土表现出更强的结构性,这是由于它在漫长的沉积过程及随后的各种地质作用过程中,使土粒间排列和各种作用力表现特有的形式和作用。
在粘性土中,敏感性指标(灵敏度)是反映粘土结构性的重要指标。
原状粘土与重塑土的无侧限抗压强度之比称为灵敏度。
图2‐8‐10 为在侧限压缩试验中,正常固结的原状土与重塑土的试验结果。
可见在在一定的压力范围内二者有明显的差别,超过一定的压力以后,两曲线趋于平行。
在图2‐8‐11 中表示了在比最优含水量更湿的情况下,用静压法和揉挤法制成压实土样的无侧限压缩试验结果。
由于静压法制样形成更强的凝絮结构,而揉挤则破坏了颗粒间的联系及结构性,二者的应力应变及强度相差很大。
图2‐8‐12 表示的是一种旧金山海滨淤泥土的原状土与扰动土的不排水试验结果。
首先将原状土样从地层中取出放在三轴压力室中,施加围压p = 80kPa(不固结)以平衡原位应力。
然后进行不排水试验直到破坏。
然后拆开三轴压力室,取出试样,在橡皮膜中就地进行重塑,再重装压力室,仍然施加80kPa围压(不固结),再加轴向荷载,得到的应力应变曲线和孔压关系见图2‐8‐12(a),这种试验分别进行了两组。
可见两种土的应力应变关系相差极大。
对两组试样,由不排水强度计算的敏感度分别为4.5 和3.1。
这种差别主要是由于二者的有效应力不同。
由于扰动土的结构破坏,使试样内超静孔压大大增加,有效应力降低。
二者的有效应力路径见图2‐8‐12(b)。
以往在土力学中研究建立的理论及模型基本是建立在对重塑土试验的基础上,因而对于土的结构性的考虑是不够的。
在自然界和工程实践中,大量存在和涉及的是原状土,因而考虑土的结构性对土的力学性质的影响是一个重要的课题。
所谓的特殊土或区域性土往往具有更强烈或特殊的结构性。
土的结构性对土的应力应变强度的影响,以及土的结构性破坏后应力应变强度性质的变化是土力学理论和实践中一个重要研究领域。
1.4.6 土的流变性粘性土的应力应变强度关系受时间的影响,这包括两个方面:一是基于有效应力原理的孔压消散和土体固结,二是土的流变性的影响。
与土的流变性有关的现象是土的蠕变与应力松弛。
所谓蠕变是指在应力状态不变的条件下,应变随时间逐渐增长的现象;应力松弛是指维持应变不变,材料内的应力随时间逐渐减小的现象。
图2‐3‐8 表示土的蠕变和应力松弛的现象。
在图2‐3‐8(a)中,在某一常应力作用下,土的应变不断增加,但当这个应力值较小时,如图中(σ1-σ3)1和(σ1-σ3)2,试样变形逐渐趋于稳定;当这个常应力较大时,则应变量会在相对稳定之后又突然加快,最后达到蠕变破坏。