平行线与相交线复习学案
- 格式:doc
- 大小:349.00 KB
- 文档页数:3

相交线与平行线学期复习教案一、教学目标1. 复习相交线与平行线的定义及性质。
2. 巩固学生对平行公理及推论的理解。
3. 提高学生解决实际问题的能力。
4. 培养学生的空间想象能力和逻辑思维能力。
二、教学内容1. 相交线与平行线的定义及性质。
2. 平行公理及推论。
3. 实际问题中的应用。
三、教学重点与难点1. 相交线与平行线的性质。
2. 平行公理及推论的应用。
3. 解决实际问题。
四、教学方法1. 采用讲解、演示、练习、讨论相结合的方法。
2. 利用多媒体课件辅助教学,增强学生的空间想象力。
3. 引导学生运用所学知识解决实际问题,提高学生的应用能力。
五、教学过程1. 导入新课:回顾上节课的内容,引导学生复习相交线与平行线的定义及性质。
2. 讲解与演示:利用多媒体课件,讲解相交线与平行线的性质,展示平行公理及推论。
3. 练习与讨论:布置练习题,让学生独立完成,进行讨论,解答疑难问题。
4. 实际问题应用:给出实际问题,让学生运用所学知识解决,引导学生将理论应用于实践。
5. 总结与反思:对本节课的内容进行总结,强调重点难点,鼓励学生反思自己的学习过程。
六、课后作业1. 巩固相交线与平行线的定义及性质。
2. 熟练运用平行公理及推论解决实际问题。
3. 总结本节课的学习收获,提出疑问。
七、教学评价1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习与作业:检查学生的练习和课后作业,评估学生对知识的掌握程度。
3. 实际问题解决:评估学生在解决实际问题时的能力,考察学生的应用水平。
八、教学资源1. 多媒体课件:展示相交线与平行线的性质、平行公理及推论。
2. 练习题:提供不同难度的练习题,巩固所学知识。
3. 实际问题:选取与生活相关的实际问题,引导学生运用知识解决。
九、教学进度安排1. 课时:2课时。
2. 教学内容:相交线与平行线的定义及性质(第1课时),平行公理及推论(第2课时)。

第五章相交线与平行线复习课教学设计学习目标:1、复习巩固相交线与平行线的有关概念和性质,使学生会用这些概念和性质进行简单的推理或计算;能用直尺、三角板、量角器画垂线和平行线;经历对本章所学知识回顾与思考的过程,将本章内容条理化、系统化。
2、通过练习,有意识地培养学生有条理的思考和表达,充分体现学生的合作交流精神。
学情分析:本班学生尖子生少,中等生较多,差生较多,部分学生学习态度学习习惯不是很好,经过半个月的《相交线与平行线》的学习,部分学生在推理中能有条理的思考和表达,证明过程能做到言之有据,但仍有少数学生仍不能进行简单推理。
学习重点:使学生形成知识结构,并运用所学的知识进行简单的推理证明。
学习难点:证明题的思考分析过程学习方法:自主探索合作交流一、预习展示:各小组将梳理的知识结构图在实物展示台上展示,并进行适当的讲解。
二、自主学习(课件出示,生独立思考后回答。
)1、如图,直线AB、CD相交于O点,∠AOE=90°.(1)∠1和∠2互为______角;∠1和∠4互为______角;∠2和∠3互为______角;∠1和∠3互为______角;∠2和∠4互为______角.(2)若∠1=20°,那么∠2=______;∠3=∠BOE-∠____=____°-____°=_____°;∠4=∠____-∠1=____°-____°=_____°.(第1题) (第2题)2、如图所示, AC ⊥BC, C 为垂足, CD ⊥AB, 点D 为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C 到AB 的距离是_______,点A 到BC 的距离是 ,点B 到CD 的距离是 ,A 、B 两点的距离是 ;3、若直线a ,b 被直线c 所截,在所构成的八个角中指出,下列各对角之间是属于哪种特殊位置关系的角?(1)∠1与∠2是___ ;(2)∠5与∠7是_____;(3)∠1与∠5是_____;(4)∠5与∠3是____ ;(5)∠5与∠4是____;(6)∠8与∠4是______;(7)∠4与∠6是____;(8)∠6与∠3是_____;(9)∠3与∠7是______;(10)∠6与∠2是______.(第3题) (第4题) (第5题)4、如图,请分别依据所给出的条件,判定相应的哪两条直线平行?并写出推理的根据.(1)如果∠2=∠3,那么________.(____________ ,____________)(2)如果∠2=∠5,那么________.(____________,____________)(3)如果∠2+∠1=180°,那么_____.(__________,____________ )(4)如果∠5=∠3,那么_________.(____________,____________)(5)如果∠4+∠6=180°,那么___.(____________,____________)(6)如果∠6=∠3,那么__________.(____________,____________)5、如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.(1)如果AB ∥EF ,那么∠2=______.理由是____________________________________.(2)如果AB ∥DC ,那么∠3=______.理由是____________________________________ .CBA(3)如果AF∥BE,那么∠1+∠2=_____.理由是______________________________.(4)如果AF∥BE,∠4=120°,那么∠5=_ .理由是_______________________.三、合作探究(小组合作探究完成)1、在下列四个图中,∠1与∠2是同位角的图是( ).图①图②图③图④(A)①② (B)①③ C)②③ (D)③④2、已知点P在直线m外,点A、B、C均在直线m上,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离是()A等于2cm B 小于2 cm C大于2cm D不大于2cm3、如图,DC∥EF∥AB,EH∥DB,则图中与∠DGE相等的角有________________________________.(第3题)(第4题)4、如图,AB∥CD,若EM平分∠BEF,FM平分∠EFD,EN平分∠AEF,则与∠BEM互余的角有( ).(A)6个 (B)5个 C)4个 (D)3个5、以下五个条件中,能得到互相垂直关系的有( ).①对顶角的平分线②邻补角的平分线③平行线截得的一组同位角的平分线④平行线截得的一组内错角的平分线⑤平行线截得的一组同旁内角的平分线(A)1个 (B)2个(C)3个 (D)4个6、把命题“对顶角相等”写成“如果…,那么…”的形式为:;7、把命题“等角的补角相等”写成“如果…,那么…”的形式为:;四、反馈检测(第一题师带领生完成,注意分析思路和板书;其余生独立完成后展示)1.已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.2.如图,∠E=∠3,∠1=∠2,求证:∠BAP 与∠4互补3.已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C.试判断∠A与∠D的数量关系并说明原因。
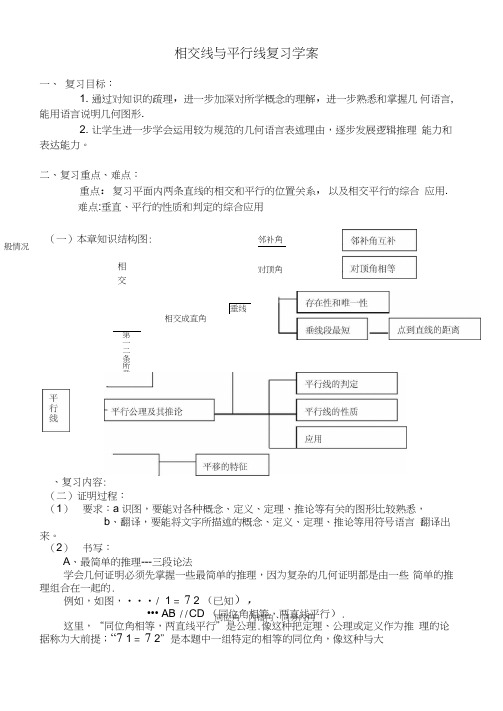
相交线与平行线复习学案一、 复习目标: 1. 通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几 何语言,能用语言说明几何图形. 2. 让学生进一步学会运用较为规范的几何语言表述理由,逐步发展逻辑推理 能力和表达能力。
二、复习重点、难点: 重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合 应用. 难点:垂直、平行的性质和判定的综合应用 、复习内容:(二)证明过程:(1) 要求:a 识图,要能对各种概念、定义、定理、推论等有关的图形比较熟悉,b 、翻译,要能将文字所描述的概念、定义、定理、推论等用符号语言 翻译出来。
(2) 书写:A 、最简单的推理---三段论法学会几何证明必须先掌握一些最简单的推理,因为复杂的几何证明都是由一些 简单的推理组合在一起的.例如,如图,•••/ 1 = 7 2 (已知),••• AB //CD (同位角相等,两直线平行).这里,“同位角相等,两直线平行”是公理.像这种把定理、公理或定义作为推 理的论据称为大前提;“7 1 = 7 2”是本题中一组特定的相等的同位角,像这种与大(一)本章知识结构图: 般情况 邻补角 相 交两条直线对顶角垂线相交成直角第一二条所截两条直线被 同位角、内错角、同旁内角前提题设部分有联系的具体对象,叫做小前提;“AB //CD”是由两个前提得出的结论•像这种由大前提、小前提推出结论的推理方式称为三段论法.B、书写步骤:在推理过程的叙述中,要分为三步书写:①讲原因,以“•••”开头,写出小前提;②讲结论,以“•••”开头,写出结果;③讲清依据,把大前提写在结果后的括号内。
练习:已知如图3, AB // CD,MN与AB,CD交于点F,EP、FQ 分别平分/ BEF 和/ DFN .求证EP / QF.证明:••• AB // CD ( )二 _______________ (••• E P、FQ 分别平分/ BEF 和/DFN (二 _____________________ (二 _____________________ ((三)习题:1一21. 如图所示,/ 1和/ 2是对顶角的图形是()A B C2、如图2-1,按各角的位置,(A )Z1与/2是同旁内角(C)Z 5与/ 6是同旁内角5.如图5-1,若/ 3=7 4,则若AB// CDJ则/ 6.已知两个角的两边分别平行,7 .如图,要说明AB // CD,需要什么条件?试把所有可能的情况写出来,并说明理由8. 如图 4-3, EF 丄GF ,垂足为 F ,/ AEF=150。

相交线与平行线复习课最新教案和讲义模版一、教学目标1. 复习巩固相交线与平行线的基本概念及性质。
2. 提高学生运用相交线与平行线解决实际问题的能力。
3. 培养学生的空间想象能力和逻辑思维能力。
二、教学内容1. 相交线与平行线的定义及性质。
2. 平行线的判定与证明。
3. 相交线的判定与证明。
4. 平行线与相交线在实际问题中的应用。
5. 巩固练习及拓展思考。
三、教学重点与难点1. 教学重点:相交线与平行线的基本概念、性质及应用。
2. 教学难点:平行线的判定与证明,相交线的判定与证明。
四、教学方法1. 采用问题驱动法,引导学生主动探究相交线与平行线的性质。
2. 利用多媒体辅助教学,直观展示相交线与平行线的关系。
3. 结合实例,让学生体会相交线与平行线在实际问题中的应用。
4. 采用小组讨论与合作交流的方式,提高学生的参与度。
五、教学过程1. 导入新课:回顾上节课的内容,引导学生复习相交线与平行线的基本概念。
2. 知识讲解:讲解相交线与平行线的性质,并通过多媒体展示实例,让学生直观理解。
3. 课堂互动:设置问题,让学生判断直线的位置关系,巩固平行线与相交线的判定方法。
4. 应用拓展:结合实际问题,让学生运用相交线与平行线解决实际问题,培养学生的应用能力。
5. 课堂练习:布置针对性的练习题,让学生巩固所学知识。
7. 课后作业:布置适量的课后作业,巩固所学知识。
六、教学评价1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习完成情况评价:检查学生课堂练习和课后作业的完成质量,评估学生对知识的掌握程度。
3. 小组讨论评价:评价学生在小组讨论中的表现,包括合作意识、交流能力等。
七、教学资源1. 多媒体教学课件:制作精美的课件,展示相交线与平行线的图形和实例。
2. 练习题库:准备一定数量的练习题,包括判断题、解答题等,用于巩固所学知识。
3. 教学素材:收集相关的实际问题,用于引导学生运用相交线与平行线解决实际问题。

相交线与平行线复习课最新教案和讲义模版一、教学目标:1. 让学生掌握相交线与平行线的定义及性质。
2. 培养学生运用相交线与平行线解决实际问题的能力。
3. 提高学生对几何图形的认识,培养学生的空间想象能力。
二、教学内容:1. 相交线的定义及性质。
2. 平行线的定义及性质。
3. 平行公理及推论。
4. 相交线与平行线在实际问题中的应用。
三、教学重点与难点:1. 重点:相交线与平行线的定义、性质及应用。
2. 难点:相交线与平行线的判定与证明。
四、教学方法:1. 采用问题驱动法,引导学生主动探究相交线与平行线的性质。
2. 利用几何画板软件,直观展示相交线与平行线的变化过程。
3. 结合实际例子,让学生学会运用相交线与平行线解决实际问题。
五、教学过程:1. 导入新课:通过复习旧知识,引导学生回顾相交线与平行线的定义及性质。
2. 讲解与演示:利用几何画板软件,展示相交线与平行线的性质及变化过程。
3. 练习与讨论:让学生自主完成相关练习题,教师引导学生讨论解题思路。
4. 应用拓展:结合实际例子,让学生运用相交线与平行线解决实际问题。
6. 布置作业:布置相关练习题,巩固所学知识。
附:讲义模版一、相交线的定义及性质1. 相交线的定义:在同一平面内,两条直线相交于一点,称这两条直线为相交线。
2. 相交线的性质:(1)相交线交点处的内角和为180度。
(2)相交线交点将两条直线分为两对对应角,对应角相等。
(3)相交线交点将两条直线分为两条对称轴。
二、平行线的定义及性质1. 平行线的定义:在同一平面内,永不相交的两条直线称为平行线。
2. 平行线的性质:(1)平行线之间的距离相等。
(2)平行线上的对应角相等。
(3)平行线上的内角和为180度。
三、平行公理及推论1. 平行公理:经过直线外一点,有且只有一条直线与已知直线平行。
2. 平行公理的推论:(1)平行线上的任意一对对应角相等。
(2)平行线上的任意一对内角和为180度。
(3)平行线之间的距离相等。

相交线与平行线复习教案一、教学目标1. 知识与技能:(1)能识别和画出相交线和平行线;(2)理解平行线的性质和判定;(3)掌握相交线的性质和判定。
2. 过程与方法:(1)通过实例和练习,提高学生对相交线和平行线的识别能力;(2)运用几何画图工具,巩固画图技能;(3)培养学生的逻辑思维能力和问题解决能力。
3. 情感态度价值观:(1)激发学生对几何学科的兴趣;(2)培养学生的团队合作意识和交流能力;(3)渗透数学美感,提高学生的审美素养。
二、教学内容1. 相交线与平行线的概念及性质;2. 平行线的判定与性质;3. 相交线的性质与判定;4. 平行线和相交线在实际问题中的应用。
三、教学重点与难点1. 教学重点:(1)相交线与平行线的识别;(2)平行线的性质和判定;(3)相交线的性质和判定。
2. 教学难点:(1)平行线的判定;(2)相交线的性质和判定。
四、教学准备1. 教具:黑板、粉笔、几何画图工具;2. 学具:学生用书、练习本、铅笔、橡皮。
五、教学过程1. 导入新课:(1)复习相关知识:直线、射线、线段的概念及性质;(2)引入相交线与平行线的概念,引导学生回顾已学知识。
2. 知识讲解:(1)讲解相交线与平行线的性质;(2)讲解平行线的判定与性质;(3)讲解相交线的性质与判定。
3. 课堂练习:(1)根据教师提供的题目,学生独立完成练习;(2)学生相互交流答案,教师进行点评。
4. 应用拓展:(1)提出实际问题,引导学生运用所学的知识解决问题;(2)学生分组讨论,展示解题过程和答案。
5. 课堂小结:(1)教师引导学生总结本节课所学内容;(2)学生分享学习收获和体会。
6. 布置作业:(1)巩固所学知识,提高平行线和相交线的识别和应用能力;(2)培养学生的自主学习能力。
六、教学策略1. 采用问题驱动的教学方法,引导学生通过观察、思考、探究,发现相交线与平行线的性质和判定方法;2. 利用几何画图工具,直观展示相交线与平行线的特点,增强学生的空间想象力;3. 通过小组合作、讨论交流,培养学生团队合作意识和交流能力;4. 设计富有思考性的练习题,激发学生的思维,提高学生解决问题的能力。
相交线与平行线复习课最新教案和讲义模版一、教学目标:1. 复习并巩固学生对相交线与平行线的概念、性质和判定方法。
2. 提高学生解决实际问题的能力,培养学生的空间想象和逻辑思维能力。
3. 培养学生合作学习、积极探究的学习态度。
二、教学内容:1. 相交线与平行线的定义和性质。
2. 相交线与平行线的判定方法。
3. 实际问题中的应用。
三、教学重点与难点:1. 重点:相交线与平行线的概念、性质和判定方法。
2. 难点:相交线与平行线在实际问题中的应用。
四、教学方法:1. 采用问题驱动法,引导学生主动探究相交线与平行线的性质和判定方法。
2. 利用多媒体辅助教学,展示实例,增强学生的空间想象力。
3. 组织学生进行小组讨论,培养学生的合作学习能力。
4. 结合练习题,巩固所学知识,提高学生的解题能力。
五、教学过程:1. 导入新课:回顾相交线与平行线的定义和性质,引导学生思考相交线与平行线在实际生活中的应用。
2. 知识讲解:讲解相交线与平行线的判定方法,并通过实例进行分析。
3. 课堂练习:布置相关的练习题,让学生独立完成,并及时给予解答和指导。
4. 小组讨论:组织学生进行小组讨论,分享各自的解题方法和心得。
5. 总结提升:总结本节课所学内容,强调相交线与平行线在实际问题中的应用。
6. 布置作业:布置适量的作业,让学生巩固所学知识。
六、教学评价:1. 通过课堂练习和课后作业,评价学生对相交线与平行线的掌握程度。
2. 观察学生在小组讨论中的表现,评价其合作学习和探究能力。
3. 结合学生的课堂表现和作业完成情况,对学生的学习态度和积极性进行评价。
七、教学资源:1. 多媒体教学课件:包括相交线与平行线的图片、实例和动画等。
2. 练习题:包括选择题、填空题和解答题等,覆盖本节课所学内容。
3. 小组讨论材料:提供相关的问题和实例,引导学生进行小组讨论。
八、教学进度安排:1. 第1-2课时:复习相交线与平行线的定义和性质。
2. 第3-4课时:讲解相交线与平行线的判定方法,并进行实例分析。
相交线与平行线(复习课)教案一、教学目标1. 知识与技能:(1)能够识别和画出相交线与平行线;(2)理解平行线的性质,能够运用平行线的性质解决问题;(3)掌握相交线的性质,能够运用相交线的性质解决问题。
2. 过程与方法:(1)通过观察、操作、交流等活动,提高学生的空间想象能力;(2)培养学生运用数学知识解决实际问题的能力。
3. 情感态度价值观:(1)培养学生对数学的兴趣,激发学生学习数学的积极性;(2)培养学生合作交流的意识,提高学生的团队协作能力。
二、教学内容1. 相交线与平行线的定义;2. 平行线的性质;3. 相交线的性质;4. 运用相交线与平行线的性质解决问题。
三、教学重点与难点1. 教学重点:(1)相交线与平行线的定义;(2)平行线的性质;(3)相交线的性质;(4)运用相交线与平行线的性质解决问题。
2. 教学难点:(1)平行线的性质;(2)相交线的性质。
四、教学准备1. 教具:黑板、粉笔、直尺、三角板;2. 学具:学生用书、练习本、铅笔、橡皮。
五、教学过程1. 导入新课(1)复习相关知识:直线、射线、线段的概念及特点;(2)引导学生回顾上节课所学内容:相交线与平行线的定义及性质;(3)提问:相交线与平行线在实际生活中有哪些应用?2. 探究与交流(1)分组讨论:让学生分组探讨相交线与平行线的性质,并总结出规律;(2)各组汇报:让学生代表汇报本组的讨论成果;(3)教师点评:对学生的讨论成果进行评价,并给予表扬。
3. 知识拓展(1)引导学生思考:在实际生活中,我们为什么需要学习和应用相交线与平行线;(2)举例说明:如建筑设计、道路规划等领域的应用。
4. 巩固练习(1)让学生独立完成练习题,检测对本节课知识的理解和掌握程度;(2)教师批改:及时批改学生的练习题,给予反馈和指导。
5. 总结与反思(1)让学生回顾本节课所学内容,总结相交线与平行线的性质及应用;(2)教师点评:对学生的学习情况进行评价,并提出改进意见。
第五章相交线与平行线复习导学案教学目标1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.3.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.重点、难点重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.难点:垂直、平行的性质和判定的综合应用.一.知识点回顾1.两直线相交所成的四个角中,有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为_____________.2.两直线相交所成的四个角中,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种关系的两个角,互为__________.对顶角的性质:______ _________.3.两直线相交所成的四个角中,如果有一个角是直角,那么就称这两条直线相互_______.垂线的性质:⑴过一点______________一条直线与已知直线垂直.⑵连接直线外一点与直线上各点的所在线段中,_______________.4.直线外一点到这条直线的垂线段的长度,叫做________________________.5.两条直线被第三条直线所截,构成八个角,在那些没有公共顶点的角中,⑴如果两个角分别在两条直线的同一方,并且都在第三条直线的同侧,具有这种关系的一对角叫做___________ ;⑵如果两个角都在两直线之间,并且分别在第三条直线的两侧,具有这种关系的一对角叫做____________ ;⑶如果两个角都在两直线之间,但它们在第三条直线的同一旁,具有这种关系的一对角叫做_______________.6.在同一平面内,不相交的两条直线互相___________.同一平面内的两条直线的位置关系只有________与_________两种.7.平行公理:经过直线外一点,有且只有一条直线与这条直线______.推论:如果两条直线都与第三条直线平行,那么_____________________.8.平行线的判定:⑴两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:_____________________________________.⑵两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:___________________________.⑶两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:________________________________________. 9.在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线_______ .10.平行线的性质:⑴两条平行直线被第三条直线所截,同位角相等.简单说成:_________________.⑵两条平行直线被第三条直线所截,内错角相等.简单说成:__________________________________.⑶两条平行直线被第三条直线所截,同旁内角互补.简单说成:____________________________________ .自我检测1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.( )2.平面内,一条直线不可能与两条相交直线都平行.( )3.两条直线被第三条直线所截,内错角的对顶角一定相等.( )4.互为补角的两个角的平行线互相垂直.( )5.两条直线都与同一条直线相交,这两条直线必相交.( )6.如果乙船在甲船的北偏西35°的方向线上, 那么从甲船看乙船的方向角是南偏东规定35°.( )6.如图,,8,6,10,BC AC CB cm AC cm AB cm⊥===那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.7.设a、b、c为平面上三条不同直线,a)若//,//a b b c,则a与c的位置关系是_________;b)若,a b b c⊥⊥,则a与c的位置关系是_________;c)若//a b,b c⊥,则a与c的位置关系是________.8.如图,已知AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°,求∠COE、∠AOE、∠AOG的度数.9.如图,AOC∠与BOC∠是邻补角,OD、OE分别是AOC∠与BOC∠的平分线,试判断OD与OE的位置关系,并说明理由.10.如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系.解:∠B +∠E =∠BCE 过点C 作CF ∥AB ,则B ∠=∠____( ) 又∵AB ∥DE ,AB ∥CF ,∴____________( ) ∴∠E =∠____( ) ∴∠B +∠E =∠1+∠2即∠B +∠E =∠BCE .11.⑴如图,已知∠1=∠2 求证:a ∥b .⑵直线//a b ,求证:12∠=∠.12.阅读理解并在括号内填注理由:如图,已知AB ∥CD ,∠1=∠2,试说明EP ∥FQ . 证明:∵AB ∥CD ,∴∠MEB =∠MFD ( ) 又∵∠1=∠2,∴∠MEB -∠1=∠MFD -∠2, 即 ∠MEP =∠______∴EP ∥_____.( )11. 已知DB ∥FG ∥EC ,A 是FG 上一点,∠ABD =60°,∠ACE =36°,AP 平分∠BAC ,求:⑴∠BAC 的大小;⑵∠P AG的大小.12. 如图,已知ABC ∆,AD BC ⊥于D ,E 为AB 上一点,EF BC ⊥于F ,//DG BA 交CA 于G .求证12∠=∠.13. 已知:如图∠1=∠2,∠C =∠D ,问∠A 与∠F 相等吗?试说明理由.。
相交线与平行线(复习课)教案一、教学目标1. 知识与技能:(1)能够识别和理解相交线与平行线的概念;(2)能够运用相交线与平行线的性质和判定定理解决实际问题。
2. 过程与方法:(1)通过观察、实践、探索等活动,加深对相交线与平行线性质的理解;(2)培养学生的空间想象能力、逻辑思维能力和解决问题的能力。
3. 情感态度与价值观:(2)培养学生团队协作、积极参与的精神风貌。
二、教学内容1. 相交线的概念及性质2. 平行线的概念及性质3. 相交线与平行线的判定定理4. 相交线与平行线在实际问题中的应用三、教学重点与难点1. 教学重点:(1)相交线与平行线的概念及性质;(2)相交线与平行线的判定定理及应用。
2. 教学难点:(1)相交线与平行线的判定定理的灵活运用;(2)解决实际问题中相交线与平行线的应用。
四、教学方法1. 采用问题驱动法,引导学生主动探究相交线与平行线的性质;2. 利用多媒体课件辅助教学,直观展示相交线与平行线的关系;3. 创设实践环节,让学生亲自动手操作,加深对知识的理解;4. 采用小组讨论法,培养学生的团队协作能力和解决问题的能力。
五、教学过程1. 导入新课:通过复习相关定义,引导学生回顾相交线与平行线的概念。
2. 知识讲解:(1)讲解相交线的性质,如相交线的夹角、对顶角等;(2)讲解平行线的性质,如平行线的距离、同位角等;(3)讲解相交线与平行线的判定定理,如同位角相等、内错角相等等。
3. 案例分析:展示实际问题,让学生运用所学的相交线与平行线的性质和判定定理解决问题。
4. 课堂练习:设计相关练习题,让学生巩固所学知识,并及时给予解答和反馈。
5. 总结提升:对本节课的主要内容进行总结,强调相交线与平行线在实际问题中的应用。
6. 作业布置:布置适量作业,让学生进一步巩固所学知识。
六、教学评价1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答情况,以及小组讨论中的表现,评价学生的积极性、合作能力和问题解决能力。
第五章 平行线与相交线复 习 学 案5.1相交线1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的系的两个角;⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角 ⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
2、垂线 ⑴定义,当两条直线相交所成的四个角 中,有一个角是 时,就说这两条直 线互相 ,其中的一条直线叫做另一 条直线的 ,它们的交点叫做垂足。
符号语言记作: 如图所示:AB CD ,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线 (与平行公理相比较记) ⑶垂线性质2:连接直线外一点与直线上各点的所有线段中, 最短。
简称: 。
3、垂线的画法:⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4、点到直线的距离 直线外一点到这条直线的 的长度, 叫做点到直线的距离记得时候应该结合图形进行记忆。
如图,PO ⊥AB ,同P 到直线AB 的距离是PO 的长。
PO 是垂线段。
PO 是点P 到直线AB 所有线段中最短的一条。
现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用。
5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念 分析它们的联系与区别 ⑴垂线与垂线段区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。
联系:具有垂直于已知直线的共同特征。
(垂直的性质)⑵两点间距离与点到直线的距离区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间。
联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离。
⑶线段与距离距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
5.2平行线 1、平行线的概念:在同一平面内,不相交的两条直线叫做 线,直线a 与直线b 互相平行,记作 2、两条直线的位置关系在同一平面内,两条直线的位置关系只有两种:⑴ ;⑵ 。
因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:①有且只有一个公共点,两直线 ; ②无公共点,则两直线 ;③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)3、平行公理――平行线的存在性与惟一性经过直线外一点,有且只有 条直线与这条直线平行 4、平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相 如左图所示,∵b ∥a ,c ∥a ∴ 注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行。
5、三线八角 两条直线被第三条直线所截形成八个角,它们构成了同位角、内 错角与同旁内角。
如图,直线b a ,被直线l 所截①∠1与∠5在截线l 的同侧, 同在被截直线b a ,的上方, 叫做 角(位置相同) ②∠5与∠3在截线l 的两旁(交错),在被截直线b a ,之间(内),叫做 角(位置在内且交错)③∠5与∠4在截线l 的同侧,在被截直线b a ,之间(内),叫做 角。
④三线八角也可以成模型中看出。
同位角是“A ”型;内错角是“Z ”型;同旁内角是“U ”型。
6、如何判别三线八角判别同位角、内错角或同旁内角 的关键是找到构成这两个角的“三 线”,有时需要将有关的部分“抽出 ”或把无关的线略去不看,有时又需要把图形补全。
7、两直线平行的判定方法 方法一 相等,两直线平行方法二 相等,两直线平行 方法三 互补,两直线平行 几何符号语言:∵ ∠3= ∴ AB ∥CD (同位角相等,两直线平行)∵ =∠2∴ AB ∥CD (内错角相等,两直线平行)∵ ∠4+ =180°∴ AB ∥CD (同旁内角互补,两直线平行)请同学们注意书写的顺序以及前因后果,平行线的判定是由角相等,然后得出平行。
平行线的判定是写角相等,然后写平行。
A B CD O P A B O a b c a b l 12 3 4 5 6 78 6 BA D 2 3 4 5 7 8 9 F E C A BC DE F 1 2 3 4BE D A CF 87654321D CB A注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”。
上述平行线的判定方法就是根据同位角或内错角“相等”或同旁内角“互补”这种“数量关系”,判定两直线“平行”这种“位置关系”。
⑵根据平行线的定义和平行公理的推论,平行线的判定方法还有两种:①如果两条直线没有交点(不相交),那么两直线平行。
②如果两条直线都平行于第三条直线,那么这两条直线平行。
③如果两条直线都垂直于第三条直线,那么这两条直线平行。
5.3平行线的性质 1、平行线的性质:性质1:两直线平行, 相等;性质2:两直线平行, 相等; 性质3:两直线平行,互补。
几何符号语言:∵AB ∥CD∴ =∠2(两直线平行,内错角相等)∵AB ∥CD∴∠3= (两直线平行,同位角相等) ∵AB ∥CD∴ +∠2=180°(两直线平行,同旁内角互补) 2、两条平行线的距离如图,直线AB ∥CD ,EF ⊥AB 于E ,EF ⊥CD 于F ,则称线段 EF 的长度为两平行线AB 与CD间的距离。
注意:直线AB ∥CD ,在直线AB 上任取一点G ,过点G 作CD 的垂线段GH ,则垂线段GH 的长度也就是直线AB 与CD 间的距离。
3、命题:⑴命题的概念:判断一件事情的语句,叫做命题。
⑵命题的组成每个命题都是 、 两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如果……,那么……”的形式。
具有这种形式的命题中,用“如果”开始的部分是 ,用“那么”开始的部分是 。
有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显。
对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式。
注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述。
4、平行线的性质与判定①平行线的性质与判定是互逆的关系 两直线平行同位角相等; 两直线平行内错角相等; 两直线平行同旁内角互补。
行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质。
典型例题:已知∠1=∠B ,求证:∠2=∠ 证明:∵∠1=∠B (已知)∴ (同位角相等, 两直线平行) ∴ (两直线平行同位角相等)注意,在了DE ∥BC ,不需要再写一次了,得到了DE ∥BC ,这可以把它当作条件来用了。
典型例题:如图,AB ∥DF ,DE ∥BC , ∠1=65°求∠2、∠3的度数解答:∵DE ∥BC (已知)∴∠ =∠1=65° (两直线平行,内错角相等)∵AB ∥DF (已知)∴ =180°(两直线平行,同旁内角互补) ∴∠3=180°- =180°- °= ° 5.4平移 1、平移变换①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的 和 完全相同。
②新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点③连接各组对应点的线段 2、平移的特征:①经过平移之后的图形与原来的图形的对应线段 (或在同一直线上)且 ,对应角 ,图形的形状与大小都没有发生变化。
②经过平移后,对应点所连的线段 (或在同一直线上)且 。
典型例题:如图,△ABC 经过平移之后成为△DEF ,那么:⑴点A 的对应点是点_________;⑵点B 的对应点是点______。
⑶点_____的对应点是点F ;⑷线段AB 的对应线段是线段_______;⑸线段BC 的对应线段是线段_______;⑹∠A 的对应角是______。
⑺____的对应角是∠F 。
解答:⑴D ;⑵E ;⑶C ;⑷DE ;⑸EF ;⑹∠D ;⑺∠ACB 。
思维方式:利用平移特征:平移前后对应线段相等,对应点的连线段平行或在同一直线上解答。
二、重点考查题型:1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )A .50°B .60°C .140°D .160° 2、如图2,已知AB ∥CD ,∠A =70°,则∠1的度数是( )A .70°B .100°C .110°D .130° 3、已知:如图3,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠ 与2∠的关系一定成立的是( ) A .相等 B .互余 C .互补 D .互为对顶角图1 图2 图34、如图4,AB DE ∥,65E ∠=,则B C ∠+∠=( ) A .135B .115C .36D .65图4 图5 图6A BC D E 1 2 3 4 A E GB C F H D A D F BEC 1 2 3D B A C 1 a b1 2 O A C D EF 2 1Ob M P N 1 2 3 A B C a b1 2 3A B E5、如图5,小明从A 处出发沿北偏东60°方向行走至B 处,又沿北偏西20方向行走至C 处,此时需把方向调整到与出发时一致,则方向的调整应是( ) A .右转80°B .左转80°C .右转100°D .左转100° 6、如图6,如果AB ∥CD ,那么下面说法错误的是( )A .∠3=∠7;B .∠2=∠6C 、∠3+∠4+∠5+∠6=1800D 、∠4=∠87、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30,那么这两个角是( ) A . 42138 、; B . 都是10; C . 42138 、或4210 、; D . 以上都不对8、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( ) A .①、②是正确的命题; B .②、③是正确命题;C .①、③是正确命题 ;D .以上结论皆错9、下列语句错误的是( ) A .连接两点的线段的长度叫做两点间的距离;B .两条直线平行,同旁内角互补C .若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D .平移变换中,各组对应点连成两线段平行且相等10、如图7,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=( )A .180B .270C .360D .54011、如图8,直线a b ∥,直线c 与a b ,相交.若170∠= ,则2_____∠= . 图8 图9 图10 12、如图9,已知170,270,360,∠=︒∠=︒∠=︒则4∠=______︒.13、如图10,已知AB ∥CD ,BE 平分∠ABC ,∠CDE =150°,则∠C =______14、如图11,已70,240∠=,则3∠= .图11 15、如图12所示,请写出能判定CE ∥AB 16、如图13,已知AB CD //,∠α17、推理填空:(每空1分,共12分)如图: ① 若∠1=∠2, 则 ∥ ( 若∠DAB+∠ABC=1800,则 ∥ ( ②当 ∥ 时, ∠ C+∠ABC=1800( )当 ∥ 时,∠3=∠C ( )18、如图,EF ∥AD ,∠1=∠2,∠BAC =70°,求∠AGD 的度数.请将解题过程填写完整.解:∵EF ∥AD (已知)∴∠2= _________ ( )又∵∠1=∠2(已知) ∴∠1=∠3( ) ∴AB ∥ _________ ( )∴∠BAC + _________ =180°( ) ∵∠BAC =70°(已知) ∴∠AGD = _________ . 19、如图,∠1=30°,AB ⊥CD ,垂足为O ,EF 经过点O .求∠2、∠3的度数.19、如图,E 点为DF 上的点,B 为AC 上的点,∠1=∠2,∠C =∠D . 试说明:AC ∥DF .20.已知,如图,CD ⊥AB 于D ,EF ⊥AB 于F ,∠1=∠2,请问DG ∥BC 吗?如果平行,请说明理由。