射影定理练习

0912射影定理练习题(总2页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
射影定理认真解答,一定要细心哟!
定义：射影定理的内容是在直角三角形中，每条直角边是这
条直角边在斜边的射影和斜边的比例中项，斜边上的高线是
两条直角边在斜边射影的比例中项
例如：公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有
射影定理如下
2,
(1) BC
=
BA•
BD
2,
(2) CB
=
CA•
CD
2。

(3) DC
=
DA•
DB
练习：
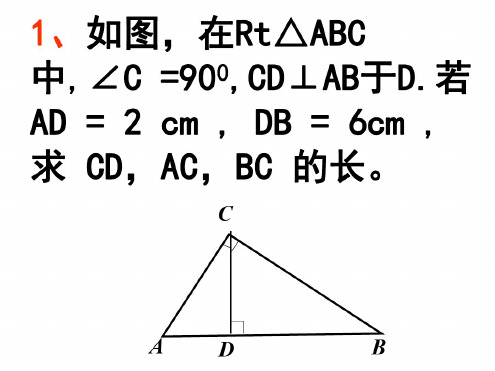
1、ABC中，90
A
∠=，AD BC
⊥于点D，AD=6，BD=12，则CD= ，AC= ，22
AB AC= 。

:
2、如图2-1，在Rt ABC中，90
∠=，CD AB
ACB
⊥，AC=6，AD=，则
BC= ．
3、已知CD是ABC的高，,
⊥⊥，如图3-1，
DE CA DF CB
求证：CEF CBA
∽
4．已知：如图，在四边形ABCD 中，∠ABC=∠ADC=90o ，DF ⊥AC 于E ，且与AB 的延长线相交于F ，与BC 相交于G 。

求证：AD 2=AB ·AF
5．如图所示，在△ABC 中，∠
ACB=90°，AM 是BC 边的中线，CN ⊥AM 于N 点，连接BN ，求证：BM 2=MN ·AM 。

A B M C
D C。

1.射影定理定义①直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．2.如图在Rt △ABC 中，∠BAC ＝90°，AD 是斜边BC 上的高，有射影定理如下：注意：直角三角形斜边上有高时，才能用射影定理！【例1】．在矩形ABCD 中，BE ⊥AC 交AD 于点E ，G 为垂足．若CG ＝CD ＝1，则AC 的长是 　．模型介绍例题精讲解：∵四边形ABCD 是矩形，∴AB ＝CD ＝1，∠ABC ＝90°，∵BE ⊥AC ，∴∠AGB ＝90°＝∠ABC ，∵∠BAG ＝∠CAB ，∴△ABG ∽△ACB ，∴＝，∴AG •AC ＝AB 2（射影定理），即（AC ﹣1）•AC ＝12，解得：AC ＝或AC ＝（不合题意舍去），即AC 的长为，故答案为：．【例2】．如图：二次函数y ＝ax 2+bx +2的图象与x 轴交于A 、B 两点，与y 轴交于C 点，若AC ⊥BC ，则a 的值为（ ）A ．﹣B ．﹣C ．﹣1D ．﹣2解：设A （x 1，0）（x 1＜0），B （x 2，0）（x 2＞0），C （0，t ），∵二次函数y ＝ax 2+bx +2的图象过点C （0，t ），∴t ＝2；∵AC ⊥BC ，∴OC 2＝OA •OB （射影定理），即4＝|x 1x 2|＝﹣x 1x 2，根据韦达定理知x 1x 2＝，∴a ＝﹣． 故选：A ．【例3】．将沿弦BC 折叠，交直径AB 于点D ，若AD ＝4，DB ＝5，则BC 的长是（ ）A．3B．8C．D．2解：连接CA、CD；根据折叠的性质，知所对的圆周角等于∠CBD，又∵所对的圆周角是∠CBA，∵∠CBD＝∠CBA，∴AC＝CD（相等的圆周角所对的弦相等）；∴△CAD是等腰三角形；过C作CE⊥AB于E．∵AD＝4，则AE＝DE＝2；∴BE＝BD+DE＝7；在Rt△ACB中，CE⊥AB，根据射影定理，得：BC2＝BE•AB＝7×9＝63；故BC＝3．故选：A．变式训练【变式1】．如图，在△ABC中，若AB＝AC，BC＝2BD＝6，DE⊥AC，则AC•EC的值是　9　．解：如图，∵在△ABC中，若AB＝AC，BC＝2BD＝6，∴AD⊥BC，CD＝BD＝3．又DE⊥AC，∴∠CED＝∠CDA＝90°．∵∠C＝∠C，∴△CDE∽△CAD．∴＝，即AC•EC＝CD2＝9．（射影定理）故答案是：9．【变式2】．如图所示，在矩形ABCD中，AE⊥BD于点E，对角线AC，BD交于O，且BE：ED＝1：3，AD＝6cm，则AE＝ cm．解：设BE＝x，因为BE：ED＝1：3，故ED＝3x，根据射影定理，AD2＝3x（3x+x），即36＝12x2，x2＝3；由AE2＝BE•ED，AE2＝x•3x；即AE2＝3x2＝3×3＝9；AE＝3．【变式3】．如图，若抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C，若∠OAC＝∠OCB．则ac的值为（ ）A．﹣1B．﹣2C．D．解：设A（x1，0），B（x2，0），C（0，c），∵二次函数y＝ax2+bx+c的图象过点C（0，c），∴OC＝c，∵∠OAC＝∠OCB，OC⊥AB，∴△OAC∽△OCB，∴，∴OC2＝OA•OB（即射影定理）即|x1•x2|＝c2＝﹣x1•x2，令ax2+bx+c＝0，根据根与系数的关系知x1•x2＝，∴，故ac＝﹣1，故选：A．【变式4】．如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F，已知DF＝5EF＝5，过C、D、F的⊙O与边AD交于点G，则DG＝____________.解：连接CF、GF，如图：在正方形ABCD中，∠EAD＝∠ADC＝90°，AF⊥DE，∴△AFD∽△EAD，∴＝，又∵DF＝5EF＝5，∴AD＝＝＝＝CD，在Rt△AFD中，AF＝＝＝，∵∠CDF+∠ADF＝90°，∠DAF+∠ADF＝90°，∴∠DAF＝∠CDF，∵四边形GFCD是⊙O的内接四边形，∴∠FCD+∠DGF＝180°，∵∠FGA+∠DGF＝180°，∴∠FGA＝∠FCD，∴△AFG∽△DFC，∴＝，∴＝，∴AG＝，∴DG＝AD﹣AG＝﹣【变式5】．如图，在△ABC中，以AC边为直径的⊙O交BC于点D，过点B作BG⊥AC交⊙O于点E、H，连AD、ED、EC．若BD＝8，DC＝6，则CE的长为　2　．解：∵AC为⊙O的直径，∴∠ADC＝90°，∵BG⊥AC，∴∠BGC＝∠ADC＝90°，∵∠BCG＝∠ACD，∴△ADC∽△BGC，∴＝，∴CG•AC＝DC•BC＝6×14＝84，连接AE，∵AC为⊙O的直径，∴∠AEC＝90°，。

名师堂八年级数学第十一讲 射影定理【选择题】1、已知直角三角形ABC 中，斜边AB=5cm,BC=2cm ，D 为AC 上的一点，DE AB ⊥交AB 于E ，且AD=3.2cm ，则DE= （ ）A 、1.24cmB 、1.26cmC 、1.28cmD 、1.3cm2、如图1-1，在Rt ABC 中，CD 是斜别AB 上的高，在图中六条线段中，你认为只要知道（ ）线段的长，就可以求其他线段的长A 、1B 、2C 、3D 、43、在Rt ABC 中，90BAC ∠= ，AD BC ⊥于点D ，若34AC AB =，则BD CD=（ ） A 、34 B 、43 C 、169 D 、9164、如图1-2，在矩形ABCD 中，1,3DE AC ADE CDE ⊥∠=∠，则E D B ∠=（ ） A 、22.5 B 、30 C 、45 D 、60【填空题】5、ABC 中，90A ∠= ，AD BC ⊥于点D ，AD=6，BD=12，则CD= ，AC=，22:AB AC = 。

6、如图2-1，在Rt ABC 中，90ACB ∠= ，CD AB ⊥，AC=6，AD=3.6，则BC= ．【解答题】7、已知CD 是ABC 的高，,DE CA DF CB ⊥⊥，如图3-1，求证：CEF CBA ∽8、已知90CAB ∠= ，AD CB ⊥，ACE ，ABF 是正三角形，求证：DE DF ⊥9、如图3-2，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，DE AM ⊥，E是垂足，求证：DE=10、已知：ΔACB为等腰直角三角形，∠ACB=900延长BA至E，延长AB至F，∠ECF=1350求证：ΔEAC∽ΔCBF11、一个钢筋三角架三边长分别为20cm，50cm，60cm，现要再做一个与其相似的钢筋三角架，而只有长为30cm和50cm的两根钢筋，要求以其中的一根为一边，从另一根截下两段(允许有余料)作为另两边，写出所有不同的截法？12、已知:如图,ΔABC中,AD=DB,∠1=∠2.求证:ΔABC∽ΔEAD13、如图，点C、D在线段AB上，且ΔPCD是等边三角形.(1)当AC，CD，DB满足怎样的关系时，ΔACP∽ΔPDB；(2)当ΔPDB∽ΔACP时，试求∠APB的度数.14、如图，四边形ABCD 、CDEF 、EFGH 都是正方形.(1)⊿ACF 与⊿ACG 相似吗？说说你的理由.(2)求∠1+∠2的度数.15、如图，4531===∠=∠∠=∠BC DE AB D B ，，，（1）ABC ∆∽ADE ∆吗？说明理由。

1.射影定理定义①直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．②每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．2.如图在Rt △ABC 中，∠BAC ＝90°，AD 是斜边BC 上的高，有射影定理如下：注意：直角三角形斜边上有高时，才能用射影定理！【例1】．在矩形ABCD 中，BE ⊥AC 交AD 于点E ，G 为垂足．若CG ＝CD ＝1，则AC的长是 ．模型介绍例题精讲①AD 2＝BD •DC ；②AB 2＝BD •BC ； AC 2＝CD •BC ．【例2】．如图：二次函数y＝ax2+bx+2的图象与x轴交于A、B两点，与y轴交于C点，若AC⊥BC，则a 的值为（）A．﹣B．﹣C．﹣1D．﹣2【例3】．将沿弦BC折叠，交直径AB于点D，若AD＝4，DB＝5，则BC的长是（）A．3B．8C．D．2➢变式训练【变式1】．如图，在△ABC中，若AB＝AC，BC＝2BD＝6，DE⊥AC，则AC•EC的值是．【变式2】．如图所示，在矩形ABCD中，AE⊥BD于点E，对角线AC，BD交于O，且BE：ED＝1：3，AD ＝6cm，则AE＝cm．【变式3】．如图，若抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C，若∠OAC＝∠OCB．则ac的值为（）A．﹣1B．﹣2C．D．【变式4】．如图，正方形ABCD中，E为AB上一点，AF⊥DE于点F，已知DF＝5EF＝5，过C、D、F 的⊙O与边AD交于点G，则DG＝____________.【变式5】．如图，在△ABC中，以AC边为直径的⊙O交BC于点D，过点B作BG⊥AC交⊙O于点E、H，连AD、ED、EC．若BD＝8，DC＝6，则CE的长为．【变式6】．如图，四边形ABCD是平行四边形，过点A作AE⊥BC交BC于点E，点F在BC的延长线上，且CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）连接AC，若∠ACD＝90°，AE＝4，CF＝2，求EC和AC的长．实战演练1．如图，在矩形ABCD中，DE⊥AC，垂足为点E．若sin∠ADE＝，AD＝4，则AB的长为（）A．1B．2C．3D．42．如图，在矩形ABCD中，BD＝2．对角线AC与BD相交于点O，过点D作AC的垂线，交AC于点E，AE＝3CE．则DE2的值为（）A．4B．2C．D．43．如图，在正方形ABCD内，以D点为圆心，AD长为半径的弧与以BC为直径的半圆交于点P，延长CP、AP交AB、BC于点M、N．若AB＝2，则AP等于（）A．B．C．D．4．如图，点P是⊙O的直径BA延长线上一点，PC与⊙O相切于点C，CD⊥AB，垂足为D，连接AC、BC、OC，那么下列结论中：①PC2＝P A•PB；②PC•OC＝OP•CD；③OA2＝OD•OP；④OA（CP﹣CD）＝AP •CD，正确的结论有（）个．A．1B．2C．3D．45．如图，在Rt△ABC中，∠A＝90°，AB＝AC＝8，点E为AC的中点，点F在底边BC上，且FE⊥BE，则CF长．6．如图，在矩形ABCD中，点E在边AD上，把△ABE沿直线BE翻折，得到△GBE，BG的延长线交CD于点F．F为CD的中点，连结CG，若点E，G，C在同一条直线上，FG＝1，则CD的长为，cos∠DEC的值为．7．如图，在平面直角坐标系中，直线y＝kx+1分别交x轴，y轴于点A，B，过点B作BC⊥AB交x轴于点C，过点C作CD⊥BC交y轴于点D，过点D作DE⊥CD交x轴于点E，过点E作EF⊥DE交y轴于点F．已知点A恰好是线段EC的中点，那么线段EF的长是．8．如图，在菱形ABCD中，过点D作DE⊥CD交对角线AC于点E，连接BE，点P是线段BE上一动点，作P关于直线DE的对称点P'，点Q是AC上一动点，连接P'Q，DQ．若AE＝14，CE＝18，则DQ﹣P'Q的最大值为．9．在矩形ABCD中，点E为射线BC上一动点，连接AE．（1）当点E在BC边上时，将△ABE沿AE翻折，使点B恰好落在对角线BD上点F处，AE交BD于点G．①如图1，若BC＝AB，求∠AFD的度数；②如图2，当AB＝4，且EF＝EC时，求BC的长．（2）在②所得矩形ABCD中，将矩形ABCD沿AE进行翻折，点C的对应点为C'，当点E，C'，D三点共线时，求BE的长．10．如图，已知⊙O的半径为2，AB为直径，CD为弦，AB与CD交于点M，将弧CD沿着CD翻折后，点A与圆心O重合，延长OA至P，使AP＝OA，连接PC．（1）求证：PC是⊙O的切线；（2）点G为弧ADB的中点，在PC延长线上有一动点Q，连接QG交AB于点E，交弧BC于点F（F 与B、C不重合）．问GE▪GF是否为定值？如果是，求出该定值；如果不是，请说明理由．11．如图1，在正方形ABCD中，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B 作BF⊥CE于点G，交AD于点F．（1）求证：△ABF≌△BCE；（2）如图2，当点E运动到AB中点时，连接DG，求证：DC＝DG；（3）如图3，在（2）的条件下，过点C作CM⊥DG于点H，分别交AD，BF于点M，N，求的值．12．在平面直角坐标系中，已知A（﹣4，0），B（1，0），且以AB为直径的圆交y轴的正半轴于点C（0，2），过点C作圆的切线交x轴于点D．（1）求过A，B，C三点的抛物线的解析式；（2）求点D的坐标；（3）设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径；若不存在，请说明理由．。

射影定理（北京习题集）（教师版）一．选择题（共1小题）1．（2017秋•平谷区校级月考）在中，，于，若，，则的值是 A ． BC ．2D ．4二．填空题（共3小题）2．（2018秋•房山区校级月考）如图，，，已知，，则图中线段的长 ， ， ．3．（2015秋•北京校级期中）如图，在中，，于，，，则 ．4．（2015秋•北京校级期中）如图，在中，，于，若，，则 ．三．解答题（共1小题）5．（2019秋•朝阳区校级期中）已知：如图，在中，，，垂足为，，，求的长．Rt ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =1BD =BC ()AB AC ⊥AD BC ⊥6AB =9BC =BD =AD =AC =Rt ABC ∆90C ∠=︒CD AB ⊥D 6CD =4BD =AD =Rt ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =8BD =CD =ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =6BD =CD射影定理（北京习题集）（教师版）参考答案与试题解析一．选择题（共1小题）1．（2017秋•平谷区校级月考）在中，，于，若，，则的值是 A ． BC ．2D ．4【分析】利用射影定理得到，然后把，代入计算即可．【解答】解：根据射影定理得，即，所以．故选：．【点评】本题考查了射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．二．填空题（共3小题）2．（2018秋•房山区校级月考）如图，，，已知，，则图中线段的长　4　， ， ．【分析】根据射影定理得，则可计算出，再计算出，然后根据计算出，利用计算出．【解答】解：，，，即，解得，，，Rt ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =1BD =BC ()2BC BD BA =g 3AD =1BD =2BC BD BA =g 21(13)BC =⨯+2BC =C AB AC ⊥AD BC ⊥6AB =9BC =BD =AD =AC =2AB BD BC =g 4BD =5CD BC BD =-=2AD BD CD =gAD 2AC CD BC =g AC AB AC ⊥Q AD BC ⊥2AB BD BC ∴=g 269BD =g 4BD =5CD BC BD ∴=-=2AD BD CD =Q g AD ∴==，故答案为4，，【点评】本题考查了射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．3．（2015秋•北京校级期中）如图，在中，，于，，，则　9　．【分析】根据射影定理列出算式，计算即可．【解答】解：，，，， 故答案为：9．【点评】本题考查的是射影定理的应用，直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．4．（2015秋•北京校级期中）如图，在中，，于，若，，则　【分析】根据射影定理列出等积式，代入已知数据计算即可．【解答】解：，，，则故答案为：【点评】本题考查的是射影定理的应用，直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．三．解答题（共1小题）5．（2019秋•朝阳区校级期中）已知：如图，在中，，，垂足为，，，2AC CD BC =Q g AC ∴==Rt ABC ∆90C ∠=︒CD AB ⊥D 6CD =4BD =AD =90C ∠=︒Q CD AB ⊥2CD AD BD ∴=g 29CD AD BD∴==Rt ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =8BD =CD =90ACB ∠=︒Q CD AB ⊥224CD AD BD ∴==g CD =ABC ∆90ACB ∠=︒CD AB ⊥D 3AD =6BD =求的长．【分析】根据射影定理列式计算即可．【解答】解：由射影定理得，，【点评】本题考查的是射影定理，直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项．CD 23618CD AD DB ==⨯=g CD ∴==。

2014级直升初二数学III 相似三角形应用——射影定理练习
姓名_________________教学班___________12.7
1．如图，菱形ABCD 中，顶点A 到边BC ，CD 的距离AE ，AF 都为5，EF=6，那么菱形ABCD 的边长为 ．
2．两个任意大小的正方形，都可以适当剪开，拼成一个较大的正方形，如用两个边长分别为a ，b 的正方形拼成一个大正方形．图中Rt △ABC 的斜边AB 的长等于 （用a ，b 的代数式表示）．
3．在Rt △ABC 中，C 为直角顶点，过点C 作AB 的垂线，若D 为垂足，若AC 、BC 为方程x 2﹣6x +2=0的两根，则AD•BD 的值等于 ．
4．如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE 、BN 于点F 、C ，过顶C 作品AM 的垂线CD ，垂足为D ．若CD=CF ，求AE AD
的值．
5．已知：如图，等腰△ABC 中AB=AC ，高AD 、BE 交于点H ，求证：4DH•DA=BC 2．
6．已知CD 是△ABC 的高，DE CA ⊥，DF CB ⊥，如图3-1，求证：CEF CBA ∽．
7．如图，已知：BD 、CE 是△ABC 的两条高，过点D 的直线交BC 和BA 的延长线于G 、H ，交CE 于F ，且∠H=∠BCF ．求证：GD 2=GF·GH ．
8．如图，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，DE AM ⊥，E 是垂足， 求证：
2224ab
DE a b =+．
9．如图，在矩形ABCD 中，DE AC ⊥，1
3ADE CDE ∠=∠，求EDB ∠度数．。

定义：射影定理的内容是在直角三角形中，每条直角边是这
条直角边在斜边的射影和斜边的比例中项，斜边上的高线是
两条直角边在斜边射影的比例中项
例如：公式Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射
影定理如下
(1)(AD)^2;=BD ·DC,
(2)(AB)^2;=BD ·BC ,
(3)(AC)^2;=CD ·BC 。

例题1：
1、ABC 中，90A ∠=，AD BC ⊥于点D ，AD=6，BD=12，则CD=，AC= ，22:AB AC = 。

2、如图1-1，在Rt ABC 中，CD 是斜别AB 上的高，在图中六条线段中，
你认为只要知道（ ）线段的长，就可以求其他线段的长
3、如图2-1，在Rt ABC 中，90ACB ∠=，CD AB ⊥，AC=6，AD=3.6，
则BC= ．
3、已知CD 是ABC 的高，,DE CA DF CB ⊥⊥，如图3-1，求证：CEF CBA ∽
变式训练：
图1—4—3，已知：BD 、CE 是△ABC 的两条高，过点D 的直线交BC 和
BA 的延长线于G 、H ，交CE 于F ，且∠H=∠BCF 。

求证：GD 2=GF ·GH 。

中考链接：
如图3-2，矩形ABCD 中，AB=a ，BC=b ，M 是BC 的中点，
DE AM ⊥，E 是垂足，求证：
DE =
创新训练：
如图1-2，在矩形ABCD 中，
1,3DE AC ADE CDE ⊥∠=∠，则EDB ∠=
Welcome !!! 欢迎您的下载，资料仅供参考！。

专项32 相似三角形-射影定理综合应用（2种类型）　一、射影定理　直角三角形斜边上的高是它分斜边所得两条线段的比例中项；且每条直角边都是它在斜边上的射影和斜边的比例中项。

如图（１）：Ｒt△ＡＢＣ中，若ＣＤ为高，则有ＣD２＝ＢＤ•AD、ＢＣ２＝ＢＤ•ＡＢ或ＡＣ２＝ＡＤ•ＡＢ。

（证明略）二、变式推广　１．逆用 如图（１）：若△ＡＢＣ中，ＣＤ为高，且有ＤＣ２＝ＢＤ•ＡＤ或ＡＣ２＝ＡＤ•ＡＢ或ＢＣ２＝ＢＤ•ＡＢ，则有∠ＤＣＢ＝∠Ａ或∠ＡＣＤ＝∠Ｂ，均可等到△ＡＢＣ为直角三角形。

　２．一般化，若△ＡＢＣ不为直角三角形，当点Ｄ满足一定条件时，类似地仍有部分结论成立。

（后文简称：射影定理变式（2）） 如图（２）：△ＡＢＣ中，D为ＡＢ上一点，若∠ＣＤＢ＝∠ＡＣＢ，或∠ＤＣＢ＝∠Ａ，则有△ＣＤＢ∽△ＡＣＢ，可得ＢＣ２＝ＢＤ•AB；反之，若△ＡＢＣ中，Ｄ为ＡＢ上一点，且有ＢＣ２＝ＢＤ•ＡＢ，则有△ＣＤＢ∽△ＡＣＢ，可得到∠ＣＤＢ＝∠ＡＣＢ，或∠ＤＣＢ＝∠Ａ。

【类型1：直角三角形中射影定理】【典例1】（2021秋•南京期末）如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，且＝．（1）求证△ACD∽△ABC；（2）若AD＝3，BD＝2，求CD的长．【解答】（1）证明：∵＝，∠A＝∠A，∴△ACD∽△ABC；（2）解：∵△ACD∽△ABC，∴∠ACD＝∠B，∵∠ACB＝90°，∴∠A+∠B＝90°，∴∠A+∠ACD＝90°，∴∠ADC＝90°，∴∠ADC＝∠BDC，∵∠ACD＝∠B，∴△ACD∽△CBD，∴＝，∴＝，∴CD＝．【变式1-1】（2022•义乌市校级开学）如图，在△ABC中，∠ACB＝90°，CD⊥AB，若AD＝4，BD＝8，则CD的长为（ ）A．4B．4C．4D．【答案】A【解答】解：∵∠ACB＝90°，∴∠A+∠B＝90°，∵CD⊥AB，∴∠DCB+∠B＝90°，∴∠A＝∠DCB，∵∠ADC＝∠CDB＝90°，∴△ADC∽△CDB，∴＝，即＝，解得：CD＝4，故选：A．【变式1-2】（2021秋•漳州期末）如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D，AD＝3，CD＝4，则BD的长为（ ）A．B．C．D．2【答案】A【解答】解：∵∠BAC＝90°，∴∠B+∠C＝90°，∵AD⊥BC，∴∠DAC+∠C＝90°，∠ADB＝∠ADC＝90°，∴∠B＝∠DAC，∴△BDA∽△ADC，∴＝，∵AD＝3，CD＝4，∴＝，解得：BD＝，故选：A．【变式1-3】（2020秋•梁平区期末）如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，下列结论中错误的是（ ）A．AC2＝AD•AB B．CD2＝CA•CB C．CD2＝AD•DB D．BC2＝BD•BA 【答案】B【解答】解：∵∠ACB＝90°，CD⊥AB于点D，∴AC2＝AD•AB，CD2＝DA•DB，BC2＝BD•BA．故选：B．【变式1-4】（2015•黄冈中学自主招生）将沿弦BC折叠，交直径AB于点D，若AD＝4，DB＝5，则BC的长是（ ）A．3B．8C．D．2【答案】A【解答】解：连接CA、CD；根据折叠的性质，知所对的圆周角等于∠CBD，又∵所对的圆周角是∠CBA，∵∠CBD＝∠CBA，∴AC＝CD（相等的圆周角所对的弦相等）；∴△CAD是等腰三角形；过C作CE⊥AB于E．∵AD＝4，则AE＝DE＝2；∴BE＝BD+DE＝7；在Rt△ACB中，CE⊥AB，根据射影定理，得：BC2＝BE•AB＝7×9＝63；故BC＝3．故选：A．【类型2：非直角三角形中射影定理】【典例2】如图，已知∠A＝70°，∠APC＝65°，AC2＝AP•AB，则∠B的度数为（ ）A．45°B．50°C．55°D．60°【答案】A【解答】解：∵∠A＝70°，∠APC＝65°，∴∠ACP＝180°﹣70°﹣65°＝45°．∵AC2＝AP•AB，∴＝．∵∠B＝∠B，∴△BAC∽△CPA．∴∠B＝∠ACP＝45°．故选：A．【变式2-1】如图，在△ABC中，点D在边AB上，若∠ACD＝∠B，AD＝3，BD＝4，则AC的长为（ ）A．2B．C．5D．2【答案】B【解答】解：∵∠ACD＝∠B，∠A＝∠A，∴△ADC∽△ACB，∴，∵AD＝3，BD＝4，∴AB＝AD+BD＝3+4＝7，∴，∴AC＝或﹣（舍去），故选：B．【变式2-2】如图，在△ABC中，点D在AB边上，∠ABC＝∠ACD．（1）求证：△ABC∽△ACD；（2）若AD＝2，AB＝6．求AC的长．【解答】（1）证明：∵∠ABC＝∠ACD，∠A＝∠A，∴△ABC∽△ACD；（2）解：∵△ABC∽△ACD，∴，∴AC2＝2×6＝12，∴AC＝2．【典例3】如图，在△ABC中，∠A＝90°，点D、E分别在AC、BC边上，BD＝CD＝2DE，且∠C+∠CDE＝45°，若AD＝6，则BC的长为 ．【答案】8【解答】解：∵∠A＝90°，∴∠ABD+∠ADB＝90°，∵BD＝CD，∴∠DBC＝∠C，∴∠ADB＝∠DBC+∠C＝2∠C，∵∠C+∠CDE＝45°∴2∠C+∠CDE＝90°，∴∠ADB+∠CDE＝90°，∴∠BDE＝90°，作DF⊥BC于F，如图所示：则BF＝CF，△DEF∽△BED∽△BDF，∴＝＝＝，设EF＝x，则DF＝2x，BF＝CF＝4x，∴BC＝8x，DE＝x，∴CD＝BD＝2x，AC＝6+2x，∵∠DFC＝∠A＝90°，∠C＝∠C，∴△CDF∽△CBA，∴＝，即＝，解得：x＝，∴BC＝8；故答案为：8．【变式3】如图，在锐角△ABC中，BD⊥AC于D，DE⊥BC于E，AB＝14，AD＝4，BE：EC＝9：2，则CD＝ ．【答案】2【解答】解：∵BD⊥AC，∴∠ADB＝90°，∴BD2＝AB2﹣AD2＝142﹣42＝180，设BE＝9x，EC＝2x，∵DE⊥BC，∴BD2＝BE•BC，即180＝9x（9x+2x），解得x2＝，∵CD2＝CE•CB＝2x•11x＝22×＝40，∴CD＝2．1.（2022秋•义乌市月考）如图，小明在A时测得某树的影长为3m，B时又测得该树的影长为2m，若两次日照的光线互相垂直，则树的高度为（ ）m．A．B．C．6D．【答案】B【解答】解：根据题意，作△EFC，树高为CD，且∠ECF＝90°，ED＝2m，FD＝3m；∵∠E+∠F＝90°，∠E+∠ECD＝90°，∴∠ECD＝∠F，∴△EDC∽△CDF，∴＝，即DC2＝ED•FD＝2×3＝6，解得CD＝m．故选：B．2．（2012•麻城市校级自主招生）如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于点E，且DE∥BC．已知AE＝2，AC＝3，BC＝6，则⊙O的半径是（ ）A．3B．4C．4D．2【答案】D【解答】解：延长EC交圆于点F，连接DF．则根据90°的圆周角所对的弦是直径，得DF是直径．∵DE∥BC，∴△ADE∽△ABC．∴．则DE＝4．在直角△ADF中，根据射影定理，得EF＝＝4．根据勾股定理，得DF＝＝4，则圆的半径是2．故选：D．3．（2022春•周村区期末）如图，在△ABC中，∠BAC＝90°，AD⊥BC于D，BD＝3，CD＝12，则AD的长为 ．【答案】6【解答】解：∵∠BAC＝90°，AD⊥BC，∴AD2＝CD•BD＝36，∴AD＝6，故答案为：6．4．（2021春•汉阴县期中）如图所示，在矩形ABCD中，AE⊥BD于点E，对角线AC，BD 交于O，且BE：ED＝1：3，AD＝6cm，则AE＝ cm．【答案】3【解答】解：设BE＝x，因为BE：ED＝1：3，故ED＝3x，根据射影定理，AD2＝3x （3x+x），即36＝12x2，x2＝3；由AE2＝BE•ED，AE2＝x•3x；即AE2＝3x2＝3×3＝9；AE＝3．5．（2022•武汉模拟）在矩形ABCD中，BE⊥AC交AD于点E，G为垂足．若CG＝CD＝1，则AC的长是 ．【答案】【解答】解：∵四边形ABCD是矩形，∴AB＝CD＝1，∠ABC＝90°，∵BE⊥AC，∴∠AGB＝90°＝∠ABC，∵∠BAG＝∠CAB，∴△ABG∽△ACB，∴＝，∴AG•AC＝AB2（射影定理），即（AC﹣1）•AC＝12，解得：AC＝或AC＝（不合题意舍去），即AC的长为，故答案为：．6．（2021秋•滦州市期中）已知关于x的方程x2﹣2（a+b）x+c2+2ab＝0有两个相等的实数根，其中a、b、c为△ABC的三边长．（1）试判断△ABC的形状，并说明理由；（2）若CD是AB边上的高，AC＝2，AD＝1，求BD的长．【解答】解：（1）∵两根相等，∴可得：4（a+b）2﹣4（c2+2ab）＝0，∴a2+b2＝c2，∴△ABC是直角三角形；（2）由（1）可得：AC2＝AD×AB，∵AC＝2，AD＝1，∴AB＝4，∴BD＝AB﹣AD＝3．7．如图，点D在△ABC的边BC上，∠ADC+∠BAC＝180°，AB＝4，BC＝8，求BD的长．【解答】解：∵∠ADC+∠BAC＝180°，∠ADC+∠ADB＝180°，∴∠ADB＝∠BAC，又∵∠B＝∠B，∴△BAD∽△BCA，∴＝，∴BA2＝BD•BC，∵AB＝4，BC＝8，∴BD＝2．即AC⋅CF＝CB⋅DF．8．（盐城校级模拟）【问题情境】如图1，Rt△ABC中，∠ACB＝90°，CD⊥AB，我们可以利用△ABC与△ACD相似证明AC2＝AD•AB，这个结论我们称之为射影定理，试证明这个定理；【结论运用】如图2，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E 在CD上，过点C作CF⊥BE，垂足为F，连接OF，（1）试利用射影定理证明△BOF∽△BED；（2）若DE＝2CE，求OF的长．【解答】【问题情境】证明：如图1，∵CD⊥AB，∴∠ADC＝90°，而∠CAD＝∠BAC，∴Rt△ACD∽Rt△ABC，∴AC：AB＝AD：AC，∴AC2＝AD•AB；【结论运用】（1）证明：如图2，∵四边形ABCD为正方形，∴OC⊥BO，∠BCD＝90°，∴BC2＝BO•BD，∵CF⊥BE，∴BC2＝BF•BE，∴BO•BD＝BF•BE，即＝，而∠OBF＝∠EBD，∴△BOF∽△BED；（2）方法一：∵BC＝CD＝6，而DE＝2CE，∴DE＝4，CE＝2，在Rt△BCE中，BE＝＝2，在Rt△OBC中，OB＝BC＝3，∵△BOF∽△BED，∴＝，即＝，∴OF＝．方法二：将△OFC绕O顺时针旋转90度得到△OGB，如图3，由△BOF∽△BED得到∠OFB＝45°，∴∠OGB＝∠OFC＝45°+90°＝135°，∵OG＝OF，∴△OGF为等腰直角三角形，∴∠OGF＝45°，∴G点在BE上，∵BG＝CF＝，∴GF＝，∴OF＝GF＝．。

专题11 射影定理-高分必刷题（解析版）射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。

射影定理是数学图形计算的重要定理，在初三各名校的数学和各地中考试题中都多次考查了这一模型的应用。

图形1.（青竹湖）如图，在Rt△ABC中，ACB∠则AC的长等于__________.【解答】解：∵AD＝6，BD＝18，∴AB＝AD+BD＝24．∵Rt△ABC中，∠ACB＝90°，CD 是AB边上的高，∴由射影定理得：AC2＝AD•AB＝6×24，∴AC＝12．故答案是：12．2.（青竹湖）如图,△ABC中,∠ACB=90∘，CD⊥AB于D. 若BC=4，BD:AD=1:3，则BD的长为33【解答】解：∵BC=4，BD:AD=1:3，．∵Rt△ABC中，∠ACB＝90°，CD是AB边上的高，∴由射影定理得：B C2＝BD•AB，∴16＝)3(xxx+，∴2=x．故答案是：A．DC BA3.（长沙中考）如图，点P 在以MN 为直径的半圆上运动（点P 不与M ，N 重合），PQ ⊥MN ，NE 平分∠MNP ，交PM 于点E ，交PQ 于点F ． （1）+＝ ．（2）若PN 2＝PM •MN ，则＝ ．【解答】解：（1）∵MN 为⊙O 的直径，∴∠MPN ＝90°，∵PQ ⊥MN ，∴∠PQN ＝∠MPN ＝90°，∵NE 平分∠PNM ，∴∠MNE ＝∠PNE ，∴△PEN ∽△QFN ，∴，即①，∵∠PNQ +∠NPQ ＝∠PNQ +∠PMQ ＝90°，∴∠NPQ ＝∠PMQ ，∵∠PQN ＝∠PQM ＝90°， ∴△NPQ ∽△PMQ ，∴②，∴①×②得，∵QF ＝PQ ﹣PF ，∴＝1﹣， ∴+＝1，故答案为：1；（2）∵∠PNQ ＝∠MNP ，∠NQP ＝∠NPM ，∴由射影定理得：PN 2＝QN •MN ，∵PN 2＝PM •MN ，∴PM ＝QN ，∴，∵，∴，∴，∴NQ 2＝MQ 2+MQ•NQ ，即，设，则x 2+x ﹣1＝0，解得，x ＝，或x ＝﹣＜0（舍去）．4.（长郡）如图，AB 为⊙O 的直径，弦CD 与AB 相交于E ，DE ＝EC ，过点B 的切线与AD 的延长线交于F ，过E 作EG ⊥BC 于G ，延长GE 交AD 于H ． （1）求证：AH ＝HD ； （2）若BFBD＝，DF ＝9，求⊙O 的半径．【解答】（1）证明：∵AB 为⊙O 的直径，DE ＝EC ，∴AB ⊥CD ，∴∠C +∠CBE ＝90°，∵EG ⊥BC ，∴∠C +∠CEG ＝90°，∴∠CBE ＝∠CEG ，∵∠CBE ＝∠CDA ，∠CEG ＝∠DEH ，∴∠CDA ＝∠DEH ，∴HD ＝EH ，∵∠A +∠ADC ＝90°，∠AEH +∠DEH ＝90°，∴AH ＝EH ，∴AH ＝HD ； （2）解：∵∠BDF ＝90°，BFBD ＝，令BD=4x ，BF=5x ，则222)5(94x x =+）（，∴2=x ，BD=12,由射影定理得：BD 2＝DF •DA ，∴144＝9×DA ，∴DA=16，又由射影定理得：AB 2＝AF •DA ，∴AB 2＝25×16，∴AB=20,即半径为10.5.(长郡)如图，△ABC 中，以AB 为直径的⊙O 分别与AC 、BC 交于点F 、D ，过点D 作DE ⊥AC 于点E ，且CE ＝FE ． （1）求证：DE 是⊙O 的切线；（2）连OE ．若OE AB ＝10，求CE 的长．【解答】证明：（1）连接DF ，OD ，过点O 作OH ⊥AC 于H ，∵DE ⊥AC ，CE ＝FE ，∴DF＝DC ，∴∠C ＝∠DFC ，∵四边形ABDF 是圆内接四边形，∴∠OBD +∠AFD ＝180°，∵∠AFD +∠CFD ＝180°，∴∠OBD ＝∠CFD ，∵OD ＝OB ，∴∠ODB ＝∠OBD ，∴∠ODB ＝∠C ，∴OD ∥AC ，∵DE ⊥AC ，∴OD ⊥DE ，又∵OD 为半径，∴DE 是⊙O 的切线；（2）∵OH ⊥AC ，DE ⊥AC ，OD ⊥DE ，∴四边形ODEH 是矩形，∴DE ＝OH ，OD ＝EH ，∵AB ＝10，∴AO ＝OB ＝OD ＝EH ＝5，∴DE ＝＝＝4，由射影定理得：DE 2＝CE ×AE,∴16＝CE （10-CE ），∴CE ＝2或8（舍去），∴CE ＝2．6.（长沙中考）如图，四边形ABCD内接于⊙O，对角线AC为⊙O的直径，过点C作AC 的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF．（1）求∠CDE的度数；（2）求证：DF是⊙O的切线；（3）若AC=2DE，求tan∠ABD的值．解：（1）∵对角线AC为⊙O的直径，∴∠ADC＝90°，∴∠EDC＝90°；（2）证明：连接DO，∵∠EDC＝90°，F是EC的中点，∴DF＝FC，∴∠FDC＝∠FCD，∵OD＝OC，∴∠OCD＝∠ODC，∵∠OCF＝90°，∴∠ODF＝∠ODC+∠FDC＝∠OCD+∠DCF＝90°，∴DF是⊙O的切线；(3)设DE＝1，则AC＝2，由射影定理得：AC2＝AD×AE,∴20＝AD（AD+1），∴AD＝4或﹣5（舍去），∵DC2＝AC2﹣AD2，∴DC＝2，∴tan∠ABD＝tan∠ACD＝＝2；7.（青竹湖）如图,在△ABC中,△C=90△，AD平分△BAC交BC于点D，O是AB边上一点，以点O为圆心，OA长为半径的圆经过点D，作DE△AB于点E，延长DE交△O于点F，连接FO并延长交△O于点G(1)求证：BC是△O的切线；(2)求证：OA2=OB△OE；(3)若AE=9，CD=3，求△ACD与△COE面积之比。