1、复合三角函数的图像

三角函数的反函数与复合函数知识点三角函数是数学中重要的函数之一，其反函数与复合函数是在学习三角函数时需要掌握的关键知识点。

本文将介绍三角函数的反函数和复合函数的概念、性质以及应用，帮助读者全面了解并掌握这些知识。

一、三角函数的反函数1. 反函数概念：三角函数的反函数是指对于给定的三角函数值，能够确定唯一的角度值。

常见的三角函数包括正弦函数sin(x)、余弦函数cos(x)和正切函数tan(x)。

它们的反函数分别称为反正弦函数arcsin(x)（或sin^(-1)(x)）、反余弦函数arccos(x)（或cos^(-1)(x)）和反正切函数arctan(x)（或tan^(-1)(x)）。

2. 反函数的定义域与值域：正弦函数、余弦函数和正切函数的定义域和值域分别为：- 正弦函数：定义域为实数集R，值域为闭区间[-1, 1]。

- 余弦函数：定义域为实数集R，值域为闭区间[-1, 1]。

- 正切函数：定义域为实数集R，值域为实数集R。

反函数的定义域与值域与原函数相反，即：- 反正弦函数arcsin(x)：定义域为闭区间[-1,1]，值域为闭区间[-π/2,π/2]。

- 反余弦函数arccos(x)：定义域为闭区间[-1,1]，值域为闭区间[0,π]。

- 反正切函数arctan(x)：定义域为实数集R，值域为开区间(-π/2,π/2)。

3. 反函数的图像与性质：反函数的图像与原函数关于直线y=x对称。

例如，正弦函数和反正弦函数的图像关于y=x对称。

反函数的性质包括：- 反函数的定义域等于原函数的值域。

- 反函数的值域等于原函数的定义域。

- 反函数的图像为原函数图像关于y=x的镜像。

二、复合函数1. 复合函数概念：复合函数是由两个或多个函数按照一定规则相互结合而成的新函数。

设有函数f(x)和g(x)，则它们的复合函数表示为(f∘g)(x)，读作"f复合g"。

2. 复合函数的定义：对于复合函数(f∘g)(x)，定义如下：(f∘g)(x) = f(g(x))3. 复合函数的性质：复合函数具有以下性质：- 复合函数的定义域由内层函数的定义域决定，且要保证内层函数的值域在外层函数的定义域之内。

i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y ＝sin x y ＝cos x图象定义域RR 值域[－1,1][－1,1]单调性递增区间：2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间：32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间：[2k π－π，2k π] (k ∈Z )递减区间：[2k π，2k π＋π] (k ∈Z )最　值x ＝2k π＋(k ∈Z )时，y max ＝1；π2x ＝2k π－(k ∈Z )时，y min ＝－1π2x ＝2k π(k ∈Z )时，y max ＝1；x ＝2k π＋π(k ∈Z ) 时，y min ＝－1奇偶性奇函数偶函数对称性对称中心：(k π，0)(k ∈Z )（含原点）对称轴：x ＝k π＋，k ∈Zπ2对称中心：(k π＋，0)(k ∈Z )π2对称轴：x ＝k π，k ∈Z （含y 轴）最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心：（含原点）(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一：先平移后伸缩方法二：先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意：平移变换或伸缩变换都是针对自变量x 而言的，因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序，否则会出现错误。

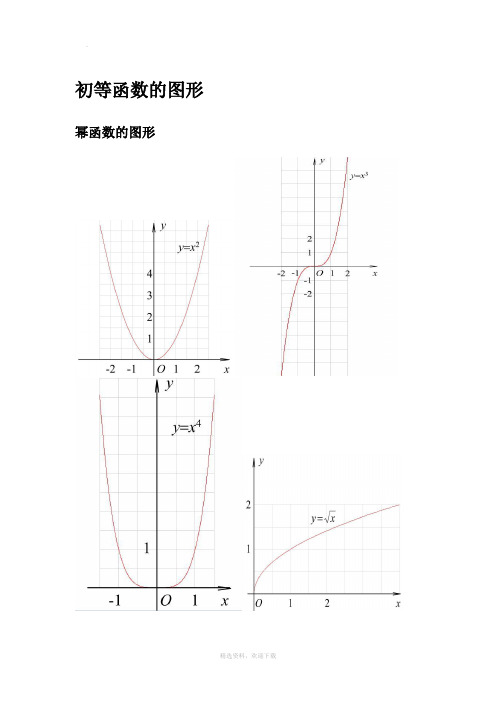
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质函数y=sinx y=cosx y=tanx y=cotx定义域R R ｛x｜x∈R且x≠kπ+2π,k∈Z｝｛x｜x∈R且x≠kπ,k∈Z｝值域［-1，1］x=2kπ+2π时y max=1x=2kπ-2π时y min=-1［-1,1］x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在［2kπ-2π,2kπ+2π］上都是增函数；在［2kπ+2π,2kπ+32π］上都是减函数(k∈Z)在［2kπ-π，2kπ］上都是增函数；在［2kπ，2kπ+π］上都是减函数(k∈Z)在(kπ-2π，kπ+2π)内都是增函数(k∈Z)在(kπ，kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数，叫做反正弦函数，记作x=arsinyy=cosx(x∈〔0,π〕)的反函数，叫做反余弦函数，记作x=arccosyy=tanx(x∈(-2π,2π)的反函数，叫做反正切函数，记作x=arctanyy=cotx(x∈(0,π))的反函数，叫做反余切函数，记作x=arccoty理解arcsinx表示属于［-2π,2π］且正弦值等于x的角arccosx表示属于［0，π］，且余弦值等于x的角arctanx表示属于(-2π,2π)，且正切值等于x的角arccotx表示属于(0，π)且余切值等于x的角性质定义域［-1，1］［-1，1］(-∞，+∞)(-∞，+∞)值域［-2π，2π］［0，π］(-2π，2π) (0，π)单调性在〔-1，1〕上是增函数在［-1，1］上是减函数在(-∞，+∞)上是增数在(-∞，+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈［-1，1］)arcsin(sinx)=x(x∈［-2π,2π］)cos(arccosx)=x(x∈［-1,1］)arccos(cosx)=x(x∈［0,π］)tan(arctanx)=x(x∈R)arctan(tanx)=x（x∈(-2π,2π)）cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈［-1,1］) arctanx+arccotx=2π(X∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinαcos （2kπ＋α）= cosαtan （2kπ＋α）= tanαcot （2kπ＋α）= cotα设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= -sinαcos（π＋α）= -cosαtan（π＋α）= tanαcot（π＋α）= cotα公式三任意角α与-α的三角函数值之间的关系：sin（-α）= -sinαcos（-α）= cosαtan（-α）= -tanαcot（-α）= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin（π-α）= sinαcos（π-α）= -cosαtan（π-α）= -tanαcot（π-α）= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin（2π-α）= -sinαcos（2π-α）= cosαtan（2π-α）= -tanαcot（2π-α）= -cotα2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明（全部）公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。