六年级按比分配应用题

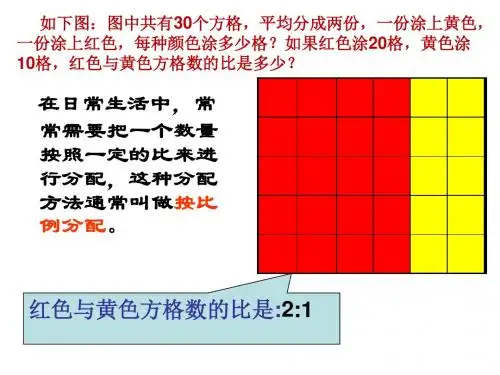
按比分配专项练习按比分配：:把一个数按着一定的比来进行分配,这种分配方法通常叫做按比分配. 归纳总结:解答按比例分配问题,要根据已知条件,把已知数量与份数对应起来,转化为求一个数的几分,一、简单的按比例分配应用题1、学校把栽480棵树的任务,按着六年级三班的人数分配给各组,一组有47人,二组有38人,三组有35人,三个组各应栽树多少棵?2、老师给班里买了90本儿童读物,按4:5分别借给一组和二组.这两个组各借书多少本?3、三条绳长的和是84米,三条绳的比是3:4:5.三条绳各长多少米?4、粮食公司有三个汽车队,甲队有6辆货车,乙队有7辆货车,丙队有8辆货车,每辆载重量相等,有378吨粮食运往外地,按运输能力分配,各队应运粮食多少吨?5、养殖专业户养鸡、鸭共6000只，鸡和鸭的比是1：11，鸡、鸭各多少只？6、一个直角三角形，两个锐角度数的比是1：4，这两个锐角各多少度？7、42名同学到面积分别是60和80平方米的菜园去帮忙种菜。

如果按面积大小分配人员，这两处菜园各应去多少名同学种菜？8、学校把540本画册按4：5借给三年级和五年级学生，每个年级各分到画册多少本？9、一个三角形铁框，三个内角度数的比是1：2：3，这个铁框的三个角分别是多少度？10、学校把864本图书按人数借给三个年级。

一年级有49人，二年级有50人，三年级有45人，三个年级各分得图书多少本？11、分别以1：2：10的石灰、硫磺和水配农药。

现在要配制农药650千克，石灰、硫磺和水各需要多少千克？12、一个等腰三角形的铁片，顶角和一个底角的度数的比是4：3，求这个等腰三角形的顶角和底角各是多少度？13、粮食局有三个汽车队，一队有9辆载重汽车，二队有8辆，三队有7辆，每辆载重量相同，有264吨粮食往外地运，按运输能力，各队应运粮食多少吨？二、稍复杂的按比例分配应用题例1．一个长方形的周长是360为米，长与宽的比是4：2，这个长方形的长和宽各是多少？例2．有840吨粮食，分给两个运输队运出去。

六年级上册数学按比分配应用题1、把300本作业按4∶5∶6分给四、五、六年级的同学，四、五、六年级的同学各得多少本作业本？解：按4：5：6来分，实际上是将300本作业平均分成4+5+6=15份，四年级得4份，五年级得5份，六年级得6份。

四年级：300÷(4+5+6)×4=80本五年级：300÷(4+5+6)×5=100本六年级：300÷(4+5+6)×6=120本。

答：四年级得80本，五年级得100本，六年级得120本。

2、一种生理盐水是把盐水和水按照1∶100配制而成，要配制这种生理盐水5050千克，需要盐水多少千克？解：1＋100＝1015050÷101＝50（千克）答：需要盐水50千克。

3、衬衣厂有40名工人，男工人与女工人的比是2：3，男女工人各有多少人？ 解：：2+3=5（份）40×25=16（人） 40×35=24（人） 答：男工人有16人，女工人有24人．4、山羊和绵羊的头数比是2∶5，山羊40头。

山羊和绵羊一共有多少头？解：40÷2＝20（头）20×（5＋2）＝140（头）答：山羊和绵羊一共有140头。

5、一种药水是用药粉和水按1∶80配制成的。

（1）40千克药粉，可配制成多少千克的药水？解：40×80＝3200（千克）3200＋40＝3240（千克）答：40千克药粉，可配制成3240千克的药水。

（2）60千克水，需要药粉多少千克？解：60÷80＝0.75（千克）答：60千克水，需要药粉0.75千克。

（3）配制这种药水1620千克，需要药粉多少千克？解：1＋80＝811620÷81＝20（千克）答：配制这种药水1620千克，需要药粉20千克。

6、一种石灰水是用石灰和水按1∶100配成的，要配制5656千克的石灰水，需石灰多少千克？解：1＋100＝1015656÷101＝56（千克）答：需石灰56千克。

六年级比的应用题型归纳一、按比例分配基础题型。

1. 学校把栽70棵树的任务，按照六年级三个班的人数分配给各班，一班有46人，二班有44人，三班有50人。

三个班各应栽树多少棵？- 解析：首先求出三个班的人数比为46:44:50 = 23:22:25。

总份数为23 +22+25 = 70份。

那么一份是70÷70 = 1棵树。

一班应栽树23×1 = 23棵，二班应栽树22×1 = 22棵，三班应栽树25×1 = 25棵。

2. 一种混凝土是由水泥、沙子和石子按2:3:5的比例混合而成的。

现有水泥12吨，需要沙子和石子各多少吨才能配制成这种混凝土？- 解析：水泥、沙子和石子的比例为2:3:5，水泥占2份，已知水泥12吨，那么一份是12÷2 = 6吨。

沙子占3份，所以沙子需要3×6 = 18吨；石子占5份，所以石子需要5×6 = 30吨。

3. 用120厘米的铁丝做一个长方体的框架。

长、宽、高的比是3:2:1。

这个长方体的长、宽、高分别是多少？- 解析：长方体的棱长总和 =（长 + 宽+高）×4，所以长 + 宽 + 高=120÷4 = 30厘米。

长、宽、高的比是3:2:1，总份数为3 + 2+1 = 6份，一份是30÷6 = 5厘米。

长是3×5 = 15厘米，宽是2×5 = 10厘米，高是1×5 = 5厘米。

4. 甲、乙、丙三个数的比是2:3:4，这三个数的平均数是18，求这三个数。

- 解析：三个数的平均数是18，则三个数的和是18×3 = 54。

甲、乙、丙三个数的比是2:3:4，总份数为2+3 + 4=9份，一份是54÷9 = 6。

甲数是2×6 = 12，乙数是3×6 = 18，丙数是4×6 = 24。

5. 某班男女生人数比是5:4，男生比女生多5人，这个班男女生各有多少人？- 解析：男女生人数比是5:4，男生比女生多5 - 4 = 1份，已知男生比女生多5人，所以一份是5人。

六年级比例的应用题及答案【篇一：六年级数学按比分配应用题及答案】>1、把300本作业按4∶5∶6分给四、五、六年级的同学，四、五、六年级的同学各得多少本作业本？解：4＋5＋6＝15答：四年级得80本，五年级得100本，六年级得120本。

2、一种生理盐水是把盐水和水按照1∶100配制而成，要配制这种生理盐水5050千克，需要盐水多少千克？解：1＋100＝101答：需要盐水50千克。

答：山羊和绵羊一共有140头。

4、一种石灰水是用石灰和水按1∶100配成的，要配制5656千克的石灰水，需石灰多少千克？解：1＋100＝101答：需石灰56千克。

5、体育室有200根跳绳，按人数分配给六年级一、二两个班，一班有52人，二班有48人，两个班各得跳绳多少根？解：52＋48＝100（人）答：一班可得跳绳104根，二班可得跳绳96根。

6、一个分数，它的分子和分母的和是40,分子和分母的比是4∶6，这个分数是几分之几？解：4＋6＝10答：这个分数是24分之16。

7、一种药水是用药粉和水按1∶80配制成的。

⑴、40千克药粉，可配制成多少千克的药水？3200＋40＝3240（千克）答：40千克药粉，可配制成3240千克的药水。

⑵、60千克水，需要药粉多少千克？答：60千克水，需要药粉0.75千克。

⑶、配制这种药水1620千克，需要药粉多少千克？解：1＋80＝81答：配制这种药水1620千克，需要药粉20千克。

8、把96分米长的铁丝焊成一个长方体框架，长、宽、和高的比是3∶2∶1，这个长方体的体积和表面各是多少？3＋2＋1＝6答：这个长方体的体积是384立方分米，表面是352平方分米。

9、五年级有140人，六年级有130人，从六年级调多少人到五年级，才能使五年级、六年级的人数比为5∶1？解：140＋130＝270（人）5＋1＝6130－45＝85（人）答：从六年级调85人到五年级。

10、甲做3000个零件比乙做2400个零件多用1小时，甲、乙的工作效率的比是6∶5。

一、已知总量和各部分之比，求各部分.1、小芳家养了28只鸡,公鸡和母鸡只数的比是2:5，公鸡和母鸡各有多少只？2、六一班和六二班订《少年科学》的份数比是3:4，两个班共订了49份。

两个班各订了多少份？3、一个足球的表面是由32块黑色五边形和白色六边形皮围成的，黑色皮和白色皮块数比是3:5。

两种颜色皮各有多少块？4、长方形的周长40米,长和宽的比是4:1.长和宽各是多少?5、一种黄铜是用锌和铜按3:7熔制而成,现在要生产这种黄铜240吨,需要锌和铜各多少吨?6、一种农药是把药粉和水按1:200配成的,要配制这种药水8040千克,需准备药粉多少千克?二、已知总量，各部分之比间接给出，求各部分各是.1、东岗小学把130棵树苗按照六年级三个班的人数,分配给各班种植。

一班有42人,二班有43人,三班有45人。

三个班各应分得树苗多少棵？2、4户居民共用一个水表,各户水费按人口数分摊.甲家4人,乙家3人,丙家6人,丁家2人,4家共付水费60元,各户应付水费多少元?3、有两块长方形草地,一块长20米,宽15米,另一块长25米,宽16米,现在有42棵花苗,按两块地的面积分栽在这两块地里,每块应栽多少棵花?4、一种饮料中的橙汁与糖的比是2:1,糖和水的比为1:9,现有120千克这种饮料,其中橙汁,糖与水各多少千克?5、已知甲乙丙三数的和是530，其中甲、乙两数之比为5:3，丙、乙两数之比为7：4，求甲乙丙三数各是多少？三、已知总量和三各部分之比，求各部分.1、学校把450本图书按2:3:4分配给四、五、六年级，四五六年级各分到多少本？2、一个长方体的棱长总和是96米,长宽高的比是4:3:5,求这个长方体的表面积和体积?3、某工程队计划挖一条1600米长的水渠，将任务按2：3：5分配给甲乙丙三个工程队,每队各挖多少米?4、某初中有学生1050人,一年级和二年级的人数比为3:4,二年级和三年级人数的比这6:7,,求一二三年级各有多少学生?四、总量间接给出，已知各部分之比，求各部分.1、把25吨粮食分配给甲乙丙三个生产小组,甲组分得7吨,乙丙两组分得的数量比是4:5,乙丙两组各分得多少吨粮食?2、两地相距360千米，甲、乙两辆汽车从两地相对开出，4小时相遇。

六年级按比例分配练习题在六年级的数学课程中，按比例分配是一个非常重要的概念和技巧。

它在日常生活中有着广泛的应用，例如在商业领域中用于计算收入分配、在家庭中用于计算开销分配等等。

充分掌握按比例分配的方法和技巧对于孩子们发展数学思维和解决实际问题至关重要。

为了帮助六年级的学生们更好地理解和掌握按比例分配的操作，本文将提供一些按比例分配的练习题，并逐步解答，帮助学生们加深对该概念的理解。

1. 练习题一：小明和小红一起完成了一项任务。

根据他们的工作量，小明完成任务的1/4，小红完成任务的3/4。

如果小明完成任务的时间是5小时，请问小红完成任务需要多长时间？解答：首先可以设小红完成任务的时间为x小时。

根据题意，小明和小红完成任务的比例是1:3，即小明完成任务的时间和小红完成任务的时间的比例是1:3。

根据题目中给出的信息，可以列出如下的比例关系式：小明的时间 / 小红的时间 = 1 / 3 （1）小明的时间 = 5小时将小明的时间代入（1），可以得到：5小时 / 小红的时间 = 1 / 3然后可以通过交叉相乘的方法解方程，得到：3 * 5小时 = 小红的时间15小时 = 小红的时间所以，小红完成任务需要15小时。

2. 练习题二：某班级共有48名学生，其中男生和女生比例是3:5。

如果班级中男生的人数是多少？解答：设男生的人数为3x，女生的人数为5x（x为比例系数）。

根据题目中给出的信息，可以列出如下的比例关系式：男生的人数 / 女生的人数 = 3 / 5 （2）男生的人数 + 女生的人数 = 48通过联立方程（2）和男生人数 + 女生人数 = 48，可以求解出男生的人数。

将方程（2）乘以5，得到：5 *（男生的人数）= 3 *（女生的人数）5x = 3x * 55x = 15x将男生人数 + 女生人数 = 48代入上式，可以得到：15x + 3x = 4818x = 48解方程得到：x = 48 / 18 = 2.67所以，男生的人数为3x = 3 * 2.67 = 8.01（约等于8人）因此，班级中男生的人数约为8人。