系统动力学_“捕食者-被捕食者”Vensim建模

系统动⼒学vensim软件使⽤说明SAVINGS AND INCOMEeffort 因果循环图快速⾃学⼿册使⽤以下步骤，建⽴如上因果循环图：1．启动Vensim ，在⼯具列点选New Model ，显⽰”Model Settings Time Bounds”对话窗⼝，再点选”OK”钮即显⽰空⽩窗⼝，就可以开始绘制因果循环图。

2．设定此绘图字型为Arial ⼤⼩为10点，操作如下：在状态列的左边点选字型名称。

因为尚未选取任何项⽬，所以显⽰是否要更改预设字型与颜⾊，点选”Yes”键，则显⽰”View Defaults” 对话窗⼝，改变”Face”为Arial 与”Size”为10，然后点选”OK”钮即可。

3．点选绘图列下的”Variable – Auxiliary/Constant” （“变量-辅助量/常量”）⼯具，然后在绘图⼯作区空⽩窗⼝，点选⼀个地⽅来放置变量”interest”，此时显⽰编辑框框，输⼊”interest”再按”Enter”键即可显⽰字号为Arial 10的”interest”。

重复此步骤来建⽴变量”savings”与”income”如上图。

(提⽰：如果拼错变量名称，则点选”Variable – Auxiliary/Constant”⼯具钮，再点选拼错变量的名称，此时显⽰编辑框框更改之即可。

如果想要完全删除变量或绘图区的其它组件，则点选绘图列下的”Delete”⼯具钮，再点选它们即可完全删除。

4．重复以上步骤来建⽴变量”work effort” 如上图。

此时”work” 与“effort”显⽰在同⼀列，若要将它们放在不同列，则拖曳⼿把(⼩圆圈)⾄左下即可调整之。

如果要改变其它特性，就按⿏标右键或同时按”control”、⿏标左键与点选”work effort”，则显⽰对话窗⼝，它提供变量多样的选择。

在对话窗⼝左上⽅，”Shape”标签选取”Clear Box”，所拖曳的⼩圆圈是改变”work effort”形状的⼿把。

系统动力学模拟软件Vensim使用指南严广乐张志刚（上海理工大学管理学院）在目前系统动力学专用的计算机模拟语言软件中，V ensim是界面非常友好的一种模拟工具，它的功能非常强大，可以运行方程数目达数千的大型模型，因此被人们广泛使用，如美国的国家模型等。

一、Vensim软件简介Vensim是美国Ventana Systems公司推出的在Windows操作平台下运行的系统动力学专用软件包，其版本在不断升级，目前最新的版本为V5.0c。

Vensim PLE是Ventana Systems公司提供的个人学习版，可到公司的网站上免费下载试用。

1.1 Vensim软件的主要特点Vensim是一款可视化的模型工具，使用该软件可以对动力学系统模型进行概念化、模拟、分析和优化。

Vensim PLE和PLE Plus是为简化系统动力学的学习而设计的Vensim的标准版本。

Vensim PLE提供了一个非常简单易用的基于因果关系链、状态变量和流图的建模方式。

Vensim用箭头来连接变量，系统变量之间的关系作为因果连接而得到确立，方程编辑器可以帮助方便地建立完整的模拟模型。

通过建立过程、检查因果关系、使用变量以及包含变量的反馈回路，可以分析模型。

当建立起一个可模拟的模型，Vensim可以从全局来研究模型的行为。

Vensim PLE适合于建立规模较小的系统动力学模型，而Vensim PLE Plus功能则更加强大，支持多视图，适合于大型的模型模拟。

Vensim提供了对所建模型的多种分析方法。

Vensim可以对模型进行结构分析和数据集分析，结构分析包括原因数分析、结果树分析和反馈回列表分析，数据集分析包括变量随时间变化的数据值及曲线图分析。

此外，Vensim还可以实现对模型的真实性检验，以判断模型的合理性，从而相应调整模型的参数或结构。

1.2 Vensim PLE的用户界面Vensim PLE的用户界面是标准的Windows应用程序界面。

系统动力学模拟软件Vensim使用指南严广乐张志刚（上海理工大学管理学院）在目前系统动力学专用的计算机模拟语言软件中，V ensim是界面非常友好的一种模拟工具，它的功能非常强大，可以运行方程数目达数千的大型模型，因此被人们广泛使用，如美国的国家模型等。

一、Vensim软件简介Vensim是美国Ventana Systems公司推出的在Windows操作平台下运行的系统动力学专用软件包，其版本在不断升级，目前最新的版本为V5.0c。

Vensim PLE是Ventana Systems公司提供的个人学习版，可到公司的网站上免费下载试用。

1.1 Vensim软件的主要特点Vensim是一款可视化的模型工具，使用该软件可以对动力学系统模型进行概念化、模拟、分析和优化。

Vensim PLE和PLE Plus是为简化系统动力学的学习而设计的Vensim的标准版本。

Vensim PLE提供了一个非常简单易用的基于因果关系链、状态变量和流图的建模方式。

Vensim用箭头来连接变量，系统变量之间的关系作为因果连接而得到确立，方程编辑器可以帮助方便地建立完整的模拟模型。

通过建立过程、检查因果关系、使用变量以及包含变量的反馈回路，可以分析模型。

当建立起一个可模拟的模型，Vensim可以从全局来研究模型的行为。

Vensim PLE适合于建立规模较小的系统动力学模型，而Vensim PLE Plus功能则更加强大，支持多视图，适合于大型的模型模拟。

Vensim提供了对所建模型的多种分析方法。

Vensim可以对模型进行结构分析和数据集分析，结构分析包括原因数分析、结果树分析和反馈回列表分析，数据集分析包括变量随时间变化的数据值及曲线图分析。

此外，Vensim还可以实现对模型的真实性检验，以判断模型的合理性，从而相应调整模型的参数或结构。

1.2 Vensim PLE的用户界面Vensim PLE的用户界面是标准的Windows应用程序界面。

SAVINGS AND INCOMEeffort 因果循环图快速自学手册使用以下步骤，建立如上因果循环图：1．启动Vensim ，在工具列点选New Model ，显示”Model Settings Time Bounds”对话窗口，再点选”OK”钮即显示空白窗口，就可以开始绘制因果循环图。

2．设定此绘图字型为Arial 大小为10点，操作如下：在状态列的左边点选字型名称。

因为尚未选取任何项目，所以显示是否要更改预设字型与颜色，点选”Yes”键，则显示”View Defaults” 对话窗口，改变”Face”为Arial 与”Size”为10，然后点选”OK”钮即可。

3．点选绘图列下的”Variable – Auxiliary/Constant” （“变量-辅助量/常量”）工具，然后在绘图工作区空白窗口，点选一个地方来放置变量”interest”，此时显示编辑框框，输入”interest”再按”Enter”键即可显示字号为Arial 10的”interest”。

重复此步骤来建立变量”savings”与”income”如上图。

(提示：如果拼错变量名称，则点选”Variable – Auxiliary/Constant”工具钮，再点选拼错变量的名称，此时显示编辑框框更改之即可。

如果想要完全删除变量或绘图区的其它组件，则点选绘图列下的”Delete”工具钮，再点选它们即可完全删除。

4．重复以上步骤来建立变量”work effort” 如上图。

此时”work” 与“effort”显示在同一列，若要将它们放在不同列，则拖曳手把(小圆圈)至左下即可调整之。

如果要改变其它特性，就按鼠标右键或同时按”control”、鼠标左键与点选”work effort”，则显示对话窗口，它提供变量多样的选择。

在对话窗口左上方，”Shape”标签选取”Clear Box”，所拖曳的小圆圈是改变”work effort”形状的手把。

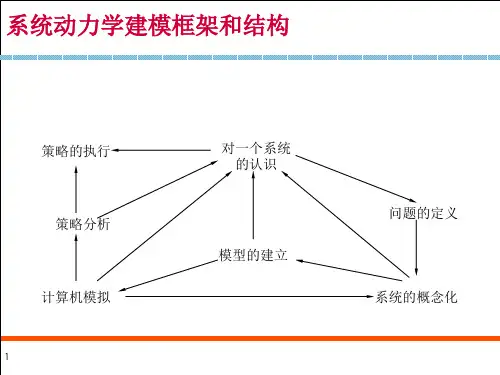
系统动力学模型构建与Vensim 软件应用教程第一部分系统动力学与Vensim 软件一、系统动力学概述系统动力学(SystemDynamics)是一门分析研究信息反馈系统的学科，也是一门认识系统问题和解决系统问题交叉的综合性的新学科。

系统动力学认为,系统的行为模式与特性主要地取决于其内部的动态结构与反馈机制。

系统:相互作用诸单元的复合体，例如:社会、经济、生态系统。

反馈:系统内同一单元或同一子块其输出与输入间的关系。

对整个系统而言，"反馈"则指系统输出与来自外部环境的输入的关系。

反馈可以从单元或子块或系统的输出直接联至其相应的输入，也可以经由媒介其他单元、子块、甚至其他系统实现。

所谓反馈系统就是包含有反馈环节与其作用的系统。

它要受系统本身的历史行为的影响，把历史行为的后果回授给系统本身，以影响未来的行为。

例如：库存控制系统是一个反馈系统，如图：发货使库存量减少，当库存低于期望水平以下一定数值后，库存管理人员即按预定的方针向。

生产部门订货，货物经一定延迟到达，然后使库存量逐渐回升。

反映库存当前水平的信息经过订货与生产部门的传递最终又以来自生产部门的货物的形式返回库存。

正反馈的特点是，能产生自身运动的加强过程，在此过程中运动或动作所引起的后果将回授，使原来的趋势得到加强；负反馈的特点是，能自动寻求给定的目标，未达到(或者未趋近)目标时将不断作出响应；具有正反馈特性的回路称为正反馈回路，具有负反馈特点的回路则称为负反馈回路(或称寻的回路)；分别以上述两种回路起主导作用的系统则称之为正反馈系统与负反馈系统(或称寻的系统)。

回路的概念最简单的表示方法是图形，系统动力学中常用三种图形表示法：系统结构框图(structurediagram)因果关系图(causalrelationshipdiagram)流图(stockandflowdiagram)系统动力学解决问题大体可分为五步：第一步要用系统动力学的理论、原理和方法对研究对象进行系统分析。

食饵为Smith增长的反应扩散捕食者-食饵模型动力学分析食饵为Smith增长的反应扩散捕食者-食饵模型动力学分析动物世界中常常存在着食饵与捕食者之间的复杂关系。

其中，反应扩散方程是一种被广泛运用在捕食者-食饵模型中的数学模型，可以用来研究食饵种群和捕食者种群之间的相互作用。

本文将通过分析食饵为Smith增长的反应扩散捕食者-食饵模型的动力学特征，探讨这种模型在生物群落的演化中的作用。

反应扩散方程是描述捕食者和食饵之间关系的一种数学方程。

在本模型中，食饵被描述为一种按照Smith增长模型增长的种群，而捕食者被描述为一种以食饵为食物的另一种种群。

模型的基本形式如下：\[\frac{\partial u}{\partial t} = D_u \Delta u +ru(1 - \frac{u}{K}) - \alpha uv\]\[\frac{\partial v}{\partial t} = D_v \Delta v -\beta uv\]在上述方程中，u代表食饵的种群密度，v代表捕食者的种群密度，t代表时间，Du和Dv分别表示食饵和捕食者的扩散系数，r为食饵的增长率，K为食饵种群的承载能力，α表示食饵被捕食后被转化为捕食者的比例，β表示食饵被捕食后导致捕食者死亡的比例。

不同的参数值设置将导致不同的动力学特征。

当θ=0时，反应项便退化为线性项，此时方程变为标准的扩散方程，描述了食饵和捕食者之间的非反馈关系。

而当θ=1时，反应项退化为饱和项，此时方程描述了食饵和捕食者之间的直接相互作用。

当0<θ<1时，反应项同时包含线性项和饱和项，此时方程描述了食饵和捕食者之间的间接相互作用。

首先，我们来探讨当θ=0时，即线性项情况下，模型的动力学特征。

由于这种情况下没有反馈作用，食饵和捕食者之间的相互作用仅仅通过扩散项来传递，模型表现出的特征是扩散过程主导。

食饵和捕食者之间将在空间上形成明显的稳定界面，且界面的波动不会扩散到整个生物群落内。

精心整理被捕食者—捕食者模型稳定性分析【摘要】自然界中不同种群之间还存在着一种非常有趣的既有相互依存、又有相互制约的生活方式：种群甲靠丰富的天然资源生存，种群乙靠捕食甲为生，形成食饵-捕食者系统，如食用鱼和鲨鱼，美洲兔和山猫，害虫和益虫等。

本文是基于食饵—捕食者之间的有关规律，建立具有自身阻滞作用的两种群食饵—捕食者模型，分析平衡点的稳定性，进行相轨线分析，并用数值模拟方法验证群食饵-MATLAB 1.2.四、符号说明)(t x /)(1t x ——食饵(食用鱼)在时刻t 的数量；)(t y /)(2t x ——捕食者(鲨鱼)在时刻t 的数量；1r ——食饵(食用鱼)的相对增长率；2r ——捕食者(鲨鱼)的相对增长率；1N ——大海中能容纳的食饵(食用鱼)的最大容量；2N ——大海中能容纳的捕食者(鲨鱼)的罪的容量；1σ——单位数量捕食者（相对于2N ）提供的供养食饵的实物量为单位数量捕食者(相对于1N )消耗2σ2N )消d 食者提供了食物，相当于使捕食者的死亡率降低，且促使其增长。

设这种作用与食饵数量成正比，于是)(t y 满足bxy dy bx d y t y +-=+-=')()((2)比例系数b 反映食饵对捕食者的供养能力。

方程(1)、(2)是在自然环境中食饵和捕食者之间依存和制约的关系，这里没有考虑种群自身的阻滞作用，是Volterra 提出的最简单的模型。

下面，我们加入种群自身的阻滞作用，在上两式中加入Logistic 项，即建立以下数学模型：⎪⎪⎭⎫⎝⎛--='22111111)(1Nx N x x r t x σ(3) ⎪⎫ ⎛21N x N x图1.数值解)(1t x ，)(2t x 的图形>>plot(x(:,1),x(:,2)),grid,图2.相轨线图形2σ>0。

七、模型分析与检验1.平衡点稳定性的分析及其实际意义：1)对)0,(11N P 而言，有p =)1(221--σr r ，q =)1(221--σr r ，故当2σ<1时，平衡点)0,(11N P 是稳定的。