高一物理动态平衡问题PPT课件

格式：ppt
大小：525.50 KB
文档页数：24

下载文档原格式

高中物理动态平衡问题课件(2024)

上。
曲线运动分类
03
平面曲线运动和空间曲线运动。
16
曲线运动中动态平衡条件
动态平衡定义
动态平衡判据
物体在曲线运动中受到的合力与运动状态相适应，使物体保持稳定的运动状态。
通过比较物体受到的合力与向心加速度的大小关系，判断物体是否处于动态平衡状态。
动态平衡条件
物体受到的合力方向与速度方向垂直，且合力大小等于物体在该点的向心加速度与质量的乘积。
表达式
$Delta E = W + Q$，其中$Delta E$ 表示系统内能的变化量，$W$表示外界对系统做的功，$Q$表示系统吸收的热量。
2024/1/26
20
能量守恒在动态平衡中意义
判断动态平衡状态
在动态平衡问题中，通过能量守恒原理可以判断系统是否处于平衡状态，以及平衡状态的稳定性
。
描述行星绕太阳运动的三大定律，包括轨道定律、面积定律和周期定律。解析方法包括万有引力定律、动量守恒等。
2024/1/26
18
05
能量守恒在动态平衡中运用
2024/1/26
19
能量守恒原理及表达式
能量守恒原理
能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为另一种形式，或者从一个物体转移到其它物体，而能量的总量保持不变。
9
典型例题解析
例题一
一个质量为m的物体放在水平地面上，受到一个斜向上的拉力F的作用，物体仍处于静止状态。求地面对物体的支持力和摩擦力。
例题二
一个质量为m的物体在水平面上做匀速直线运动，受到一个与运动方向相反的恒力F的作用。求物体的加速度和经过时间t后的速度。
2024/1/26

高一物理物体的平衡PPT精品课件

图4－1
【精讲精析】此题为动态平衡问题．结点O受三力作用，其向下拉力为恒力，大小为mg，绳OA拉力方向不变，大小变化，而OB绳上拉力的大小和方向均变化．OA绳与OB绳对O点拉力的合力G′大小为mg，方向竖直向上．两拉力的大小和方向，如图 4－2所示，由图可知FB先减小后增大，当FB⊥FA时 FB最小，而FA一直增大．
本章优化总结
知识网络构建
本
章
优
专题归纳整合
化
总
结
章末综合检测
知识网络构建
专题归纳整合
动态平衡问题的求解
处理共点力作用下的动态问题的方法就是在原来处理平衡问题的基础上，注意分析由于某一个物理量的变化，而带来的其他变化，可用图解法，也可用数学讨论法求解．
例1 用三根轻绳将质量为m的物块悬挂在空中，如图4－1所示，已知绳AO和BO与竖直方向的夹角都是30°，若想保持A、O两点的位置不变，而将B点下移至OB水平，则此过程中( ) A．OB绳上的拉力先增大后减小 B．OB绳上的拉力先减小后增大 C．OA绳上的拉力先增大后减小 D．OA绳上的拉力不断减小
图4－ 4
Fcosθ－F2－F1cosθ＝0① Fsinθ＋F1sinθ－mg＝0② 由①②式得
F＝smingθ－F1③ F＝2cFo2sθ＋2msingθ④ 要使两绳都能绷直，则有
F1≥0⑤ F2≥0⑥
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
例2 如图4－3所示，物体的质量为2 kg，两根轻绳AB和AC的一端连接于竖直墙上，另一端系于物体上，在物体上另施加一个方向与水平方向成θ ＝60°的拉力F，AB、AC的夹角也为θ，若要使绳都能伸直，求拉力F的大小范围．

物理人教版(2019)必修第一册第三章专题：动态平衡(共23张ppt)

两个力大小、方向均不确定，但是这
两个力的方向夹角保持不变。
【例题】
如图所示，装置中两根细绳拴住一球，保持两细绳间的夹角θ=120°
不变，若把整个装置顺时针缓慢转过90°，则在转动过程中，CA绳的
拉力FT1，CB绳的拉力FT2的大小变化情况是
A.FT1先变小后变大
B.FT1先变大后变小
C.FT2先变小后变大
，当FN1和FN2垂直时，弹力FN2最小，故选项B、C
正确，A、D错误。
02
解析法
（2）解析法：根据平衡关系式分析力的变化
模型：
（1）一个力大小、方向不变。
（2）其它二个力的方向均发生变化，相互垂直
解题思路：对研究对象的任意状态进行受力分析，建立平衡方
程，然后根据某一物理量的变化（一般是角度变化）确定待求
(多选)如图所示，在倾角为α的斜面上，放一质量
为m的小球，小球和斜面及挡板间均无摩擦，当挡
板绕O点逆时针缓慢地转向水平位置的过程中( )
A．斜面对球的支持力逐渐增大
B．斜面对球的支持力逐渐减小
C．挡板对小球的弹力先减小后增大
D．挡板对小球的弹力先增大后减小
解析：对小球受力分析知，小球受到重力mg、斜面
01
图解法
（1）图解法：通过力的矢量图分析力的变化
模型：当物体受到三个共点力保持平衡时，其中一个力的大小
方向都不变，一个力的方向不变，一个力大小方向均改变
情况1：一个力恒定，方向
不变的力与恒力垂直，构建
直角三角形
情况2：一个力恒定，方向
不变的力与恒力不垂直，
构建三角形，当恒力之外
的两力垂直时，有极值
∆OBA
N
F
T

动态平衡完整版PPT课件

(1)若拖把头在地板上匀速移动，求推拖把的力的大小． (2)设能使该拖把在地板上从静止刚好开始运动的水平推力与此时地板对拖把的正压力的比值为 λ. 已知存在一临界角 θ0，若 θ≤θ0，则不管沿拖杆方向的推力多大，都不可能使拖把从静止开始运动．求这一临界角的正切 tanθ0.
μ (1)sinθ－μcosθ mg (2) λ
动滑轮A下．吊变一大重B物．，变不小计C．一不切变摩擦D，．那无么法细确线定上张力的变化情况为B
变式1 如以以下图所示，不可伸长的细线一端固定于竖直墙上的O点，拉力F通过一个轻质定滑轮和轻质动滑轮竖直作用于细线的另一端，假设重物M在力
F的作用下缓缓上升，拉力F的变化情A况为
A．变大 B．变小 C．不变 D．无法确定
力为F2，那么 A
A．坐着比躺着时F1大 B．躺着比坐着时F1大 C．坐着比躺着时F2大 D．躺着比坐着时F2大
第3讲受力分析、共点力作用下物体的平衡
复习目标 1.掌握临界与极值问题的常用方法第3课时
考点三平衡中的临界与极值问题
例 4 如图所示，一质量 m ＝0.4 kg 的小物块，以 v0＝2 m/s 的初速度，在与斜面成某一夹角的拉力 F 作用下，沿斜面向上做匀加速运动，经 t＝2 s 的时间物块由 A 点运动到 B 点，A、B 之间的距离 L＝10 m．已知斜面倾角 θ＝30°，物块与斜面之间的动摩擦因数 μ＝ 33.重力加速度 g 取 10 m/s2.
当堂训练
（14 分）(2015·山东德州五校高三联考)如图所示，楼梯口一倾斜的天花板与水平地面成 37°，一装潢工人手持木杆绑着刷子粉刷天花板，工人所持木杆对刷子的作用力始终保持竖直向上，大小为 F＝10 N，刷子的质量为 m＝0.5 kg，刷子可视为质点，刷子与天花板间的动摩擦因数 μ＝0.5，天花板长为 L＝4 m，取 g＝10 m/s2，试求：(sin 37°＝0.6，cos 37°＝0.8) (1)刷子沿天花板向上的加速度大小； (2)工人把刷子从天花板底端推到顶端所用的时间。

物理人教版(2019)必修第一册3.5.2共点力的平衡(动态平衡)(23张ppt)

F3cosGFra bibliotekcos
减小
F2 F3
F2 F3tan Gtan 减小
解析法应用一般步骤：
（1）选某一状态对物体进行受力分析；（2）将其中两力合成，合力与第三个力等大反向；
解析法适用于有特殊三角形的时候（直角始终存在）。
（3）列平衡方程求出未知量与已知量的关系表达式；（4）根据已知量的变化情况来确定未知量的变化情况。
五、动态平衡问题的处理方法
1.解析式法 2.图解法--平行四边形
3.图解法----三角形定则（适用于三力动态平衡）（1）一恒一定向：
（2）一恒一定值：一恒力（大小方向均不变）、一定值力
（大小不变，方向变化）、一变力（大小方向都变）。判断另一个力的大小变化
五、动态平衡问题的处理方法
3.图解法----三角形定则（适用于三力动态平衡）
A.绳与竖直方向的夹角为θ时，F=mgcosθ B. 小球沿滑圆环上升过程中，轻绳拉力逐渐增大 C. 小球沿光滑圆环上升过程中，小球所受支持力逐渐增大 D. 小球沿光滑圆环上升过程中，小球所受支持力大小不变
六、易混淆问题
1.轻绳“死结”、“活结”问题
轻绳：绳的质量不计，伸长忽略不计，绳上任何一个横截面两边相互作用的拉力叫做“ 张力”，轻绳只有两端受力时，任何一个横截面上的张力大小都等于绳的任意一端所受拉力的大小，即同一轻绳张力大小处处相等。
不变、大小变）、一变力（大小方向都变）。判断定向力和另一个变力的大小变化
方法步骤： ①确定恒力、定向力、第三力 ②画出恒力，从恒力末端画出与定向力同方向的虚线，将第三力平移与恒力、定向力构成矢量三角形。 ③根据题中变化条件，比较这些不同形状的矢量三角形，判断各力的大小及变化。

物理人教版(2019)必修第一册3.5.2共点力的平衡(动态分析)(共20张ppt)

3.5.2共点力平衡的动态分析
学习目标
1. 了解共点力动态平衡分析的特点和方法； 2. 能够掌握矢量三角形法、相似三角形法、拉密定理和凉
衣架模型等方法，能够熟练运用方法解决动态平衡问题。
一、矢量三角形法
方法规律总结：主要解决三力平衡问题。 1.一个力是恒力，大小和方向不变。 2.另一个方向不变。 3.第三个力大小和方向改变。
பைடு நூலகம்
间的夹角θ＝120°不变，若把整个装置顺时针缓慢转过90°，
则在转动过程中，CA绳的拉力F1、CB绳的拉力F2的大小变化情
况是( )
A.F1先变小后变大 B.F1先变大后变小
C.F2一直变小
D.F2最终变为零
拉密定理法—练
2.如图所示，球面光滑的半球形物体放在水平面上。一个可视为质点的物块放在球面上在与半球面切线平行的力F作用下处于静止状态，此位置与球心O的连线与水平方向的夹角为 30°。现保持F的始终与半径垂直，改变其大小，使物块沿球面缓慢运动到球的顶端，此过程半球形物体始终不动，则（） A.F不断增大 B.F不断减小 C.球面对物块支持力先增大后减小 D.球面对物块支持力不断减小
力为G的物体，且B端系有一根轻绳并绕过定滑轮，用力F拉绳
，开始时∠BCA>90°，现使∠BCA缓慢变小，直到∠BCA＝30°.
此过程中，轻杆BC所受的力( )
A.逐渐减小
B.逐渐增大
C.大小不变
D.先减小后增大
相似三角形法—练 2.(多选)如图所示，质量均为m的小球A、B用劲度系数为k1的轻弹簧相连，B球用长为L的细绳悬挂于O点，A球固定在O点正下方，当小球B平衡时，细绳所受的拉力为FT1，弹簧的弹力为F1；现把A、B间的弹簧换成原长相同但劲度系数为k2(k2＞k1)的另一轻弹簧，在其他条件不变的情况下仍使系统平衡，此时细绳所受的拉力为FT2，弹簧的弹力为F2.则下列关于FT1与FT2、F1与F2大小的比较，正确的是( ) A.FT1＞FT2 B.FT1＝FT2 C.F1＜F2 D.F1＝F2

3.5共点力平衡(动态平衡)课件-高一上学期物理人教版

已知木块质量m,在F的作用下静止，斜面倾角度，物体与斜面的动摩擦因数为μ,求推力的范围。（设最大静摩擦力等于滑动摩擦力）
F 思考与提醒：F最小值能否为0？
分类讨论μ＜tanα时当μ≥tanα时？
随着F增大，f静会如何变化？
当μ≥tanα Fmin=0 此时摩擦力向上 f=mgsinα
若F水平呢
F 当Fmμa＜x=tmagnsαinαF+μmimn=gmcogssαinα-摩μm擦g力co向sα下f=μmgcosα
1【解斜:面由模平型衡】条总件结得μ, 反应了斜面粗糙程度 μ＞垂t直an斜θ面物：体支可持以力静N止=G在co斜sθ面上 μ=沿t斜an面θ物体：刚好摩静擦止力在f=斜Gs面in上θ，也可匀速下滑 μ＜因tfa=nμθN物体无法静止在斜面上，此时不处于平衡态
联立得μ=f/N=tanθ
多力平衡的处理----正交分解
F 始终不变 FA 一直增大 FB 先增大后减小
三力平衡一个力恒力，另外两个力夹角不变（画圆）技巧：画平四找三角，三角形外接圆，恒力对恒角，定弦对定角注意：直径对应最长的弦长，直径对的圆周角90度
四个力正交分解解析式法
导50页针对训练2. （多选）如图所示，一个人通过光滑定滑轮拉住一个木块，人和木块均静止；当人向右跨了一步后，人与重物重新保持静止，下述说法中正确的是
回顾受力分析步骤
1明确研究对象受力少的整体?隔离? 2按顺序分析其他物体对研究对象的力
技巧优先关注物体运动状态保持静止/缓慢移动=平衡=合外力为0=加速度为0
①已知力 ②非接触力 ③ 接触力弹力顺时针绕一圈看几个接触面/点
方向
大小
压支N 垂直于接触面绳子T 只能拉

高中物理必修一动态平衡课件

C
• C. N大小将不变
• D. N大小将增大
22
正弦定理法
• 例：两个可视为质点的小球a和b，用质量可忽略
的刚性细杆相连，放置在一个光滑的半球面内，如图所示。己知小球a和b的质量之比为，细杆长
度是球面半径的倍。两球处于平衡状态时，细杆与水平面的夹角θ是（）
• A．450
B．300
• C．22.50 D D．150
极值法没找到例题
19
跟踪训练：一轻杆BO，其O端用光滑铰链铰于固定竖直杆AO上，B端挂一重物，且系一细绳，细绳跨过杆顶A处的光滑小滑轮，用力F拉住，如图所示. 现将细绳缓慢往左拉，使杆BO与杆AO间的夹角θ 逐渐减少，则在此过程中，拉力F及杆BO所受压力 FN的大小变化情况是( )
A、FN先减小，后增大
小变化情况是( ) A．F不变，FN增大 B．F不变，FN减小 C．F减小，FN不变 D．F增大，FN减小
14
3.解析法解题步骤
1 明确研究对象。 2 分析物体的受力。 3 找一个大小和方向不变的力作为另外两个力的合力（也可简化为矢量三角形）。 4 三力构成的矢量角函数表示 6 由角的变化判断变力的变化情况
AC （）
A. 绳子的拉力F不断增大 B. 绳子的拉力F不变 C. 船所受的浮力不断减小 D. 船所受的浮力不断增大
注意：四个力只能用正
Fcosθ=f…①
交分解解析法
Fsinθ+F浮=mg…②
船在匀速靠岸的过程中，θ
增大，阻力不变，根据平衡
方程①知，cosθ减小，绳子
的张力增大，根据平衡方程
②知，拉力F增大，sinθ增
BC 过程中,下列说法正确的是 (
)

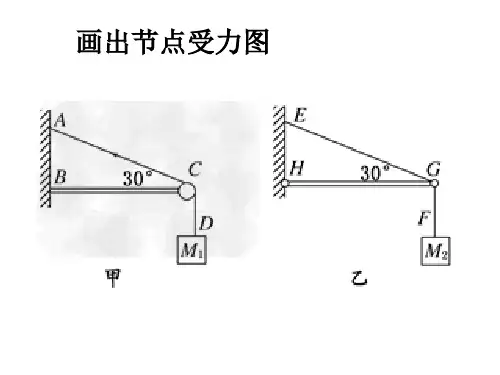
高中物理课件-动态平衡

AB
B．逐渐减小
O
C
C．逐渐增大
D．OB 与 OA 夹角等于 90o 时，OB 绳上张力最大
• “相似三角形”在物理中的应用
• “相似三角形”的主要性质是对应边成比例，对应角相等。在物理中，一般地，当涉及到矢量运算，又构建了三角形时，可考虑用相似三角形。下面以静力学为例说明其应用。
例4. 如图7所示，在半径为R的光滑半球面上高h处悬挂一定滑轮，重力为G的小球用绕过滑轮的绳子被站在地面上的人拉住，人拉动绳子，在与球面相切的某点缓缓运动到接近顶点的过程中，试分析小球对半球的压力和绳子拉力如何变化。
动态平衡问题的分析
【例 2】如图所示，两根等长的绳子 AB 和 BC 吊一重物静止，两根绳子与水平方向夹角均为 60°.现保持绳子 AB 与水平方向的夹角
解析解法一：对力的处理(求合力)采用合成法，应用合力为零求解时采用图解法(画动态平行四边
不变，将绳子 BC 逐渐缓慢地变化到沿水平形法)．作出力的平行四边形，如图甲所示．由图
方向，在这一过程中，绳子 BC 的拉力变化可看出，FBC 先减小后增大．
情况是
(B )
A．增大
B．先减小后增大
C．减小
பைடு நூலகம்
D．先增大后减小
甲
练3：在“验证力的平行四边形法则”实验中,如图所示, 用AB两弹簧秤拉橡皮条结点O,使其位于E处,此时(α+ β) = 900,然后保持A的读数不变,当α角由图中所示的值逐渐减小时,要使结点仍在E处,可采取的办法是（）
动态平衡问题的分析
解析 (解析法)如图所示，因为 FN1＝FN1′＝tamngθ，FN2＝FN2′ ＝smingθ，随 θ 逐渐增大到 90°， tan θ、sin θ 都增大，FN1、FN2 都逐渐减小，所以选项 B 正确。

物体的动态平衡问题课件-高一上学期物理人教版(2019) 必修第一册

角度2：力的极大值
方法：辅助圆法——直径是圆中最长的一条弦
范例2.已知物体在共点、共面的三个力F、F1、F2的作用下处于平衡状态，其中
F=10N，F1、F2的夹角为1500,则F2的最大值是 B
A、10N
B、20N
C、30N
D、40N
F2 30o
F1
F2=2F=20N
F
类型二角度极大值
方法：辅助圆法，作圆的切线——切线张角最大
试分析两绳上的张பைடு நூலகம்变化情况
TB
OA绳上的张力TA先变小在变大
TA
OB绳上的张力TB一直变小
TG
2.如图，保持OA绳方向不动。OB绳的B端在半圆形支架上逆时针滑至竖直方向，
试分析两绳上的张力变化情况
TB
OA绳上的张力TA一直变小 OB绳上的张力TB一直变小
TA TG
3.(教材改编）在光滑墙壁上用网兜把足球挂在A点，足球与墙壁的接触点为 B。若
范例1、一质量为m的物体在外力F的作用下恰能静置与倾角为30°的光滑斜面上，
则外力F的值可能为（ BD ）
A．0.2mg B．1.5mg
FN
C． mg D． mg
变式训练
可得：Fmin=
F mg
1、将一质量m=1kg的小球用细线悬挂于固定点O，小球在一外力F的作用下平衡时拉线与竖直方向的夹角θ=30°，则该F的大小（取g=10m/s2）可能是( AB ) A、7N B、5N C、3N/C D、1N
FTMN θ
θ= π-α
D．OM上的张力先增大后减小
FTMN= 0
θ
θ
FTMN
FT=G
FTMN
2.如图，柔软轻绳ON的一端O固定，其中间某点M拴一重物，用手拉住绳的另一端N，

高一物理《力的动态平衡》PPT课件可修改全文

是( AB)
A.绳的右端上移到 b′，绳子拉力不变 B.将杆 N 向右移一些，绳子拉力变大 C.绳的两端高度差越小，绳子拉力越小 D.若换挂质量更大的衣服，则衣架悬挂点右移
力的动态平衡
2.[江苏南京外国语学校 2022 高一上期中]如图所示，在竖直平面内一根不可伸长的柔软轻绳通过光滑的
轻质滑轮悬挂一重物．轻绳一端固定在墙壁上的 A 点，另一端从墙壁上的 B 点先沿着墙壁缓慢移到 C 点，
[答案]
（1） 33G （2）12G
共点力平衡中的临界、极值问题
对点训练 4 课堂上，老师准备了“L”形光滑木板和三个完全相同、外表面
光滑的匀质圆柱形积木，要将三个积木按图示（截面图）方式堆放在木板
上，则木板与水平面夹角 θ 的最大值为
（ A）
A．30°
B．45°
C．60°
D．90°
共点力平衡中的临界、极值问题
2cos θ 上端 D 的过程中，θ增大，cos θ减小，则 F 变大，故 A 正确，B 错误．在轻绳的右端从直杆最上端 D 移到 C 点的过程中，设两绳的夹角为 2α，轻绳总长为 L，两直杆间的距离为 s，由数学知识得到 sin α＝错误!，L、s 不变，则α保持不变．再根据平衡条件可知，F 保持不变．所以由 D 到 C 的过程中绳中拉力大小变化的情况是 F 保持不变，故 D 正确，C 错误．
确的是( BC )
A．F1 逐渐增大
B．F1 先增大后减小
C．F2 逐渐减小
D．F2 先减小后增大
力的动态平衡
正弦定理法、动态圆解决两个力的夹角不变的动态问题
9．(多选)如图所示，两根轻绳一端系于结点 O，另一端分别系于固定环上的 A、B 两点，O 点下面
悬挂一物体 M，绳 OA 水平，拉力大小为 F1，绳 OB 与 OA 夹角α＝120°，拉力大小为 F2.将两绳同时缓慢顺

物理人教版(2019)必修第一册3.5共点力的平衡-动态平衡(共23张ppt)

过定滑轮后用力拉住，使小球静止，如图，现缓慢地拉绳，在使小球由A到B的过
程中，半球对小球的支持力FN和绳对小球的拉力T的大小变化的情况是（ A ）
A.FN不变，T变小
B.FN不变，T先变大后变小
C.FN变小，T先变小后变大 D.FN变大，T变小
思考：平衡状态的小球受到哪些力？各力分别有什么特点？
【解析】设人和物体A质量分别为m、M，由题意可知绳的拉力等于Mg，人拉绳
的力F3与绳的张力大小相等，故人拉绳的力F3=Mg不变。
取人为对象，受力如图所示，并建立直角坐标系。由平衡条件可得：
F2-F3′ cosθ=0， F1′＋F3′sinθ=mg
由牛顿第三定律可知
F1′=F1，F3′=F3 解得 F1=mg-Mgsinθ，
O
F2
三角形的三条边中，首尾相接的两个边表示分力，第三个表示合力
2.闭合三角形
实例：一根细线系着一个小球，细线上端固定在横梁上。给小球施加力F，小球
平衡后细线跟竖直方向的夹角为θ。
T
构建闭合三角形：
三个平衡力G、F和T，恒力G保持不动，将方向恒定的力T沿着作用线滑移、转动的力F 平移，从而构成首尾相接的闭合三角形。
F2=Mgcosθ 由F1、F2 的函数表达式可知，当θ减小时，F1、F2增大。
故本题正确选项为B。
课堂评价
1.如图所示，质量为m的小球被轻绳系着，光滑斜面倾角为θ，向左缓慢推动劈
直到悬绳与斜面平行过程中（ D ）
A.绳上张力先增大后减小 B.斜劈对小球支持力减小 C.绳上张力先减小后增大 D.斜劈对小球支持力增大
的示数不变而减小β时，为保持结点O位置不变，可采取的办法是（ AB ）

人教版高中物理必修一课件：物体的动态平衡问题+(共21张PPT)

例3：如图所示，人站在岸上通过定滑轮用绳牵引小船，若水的阻力恒定不变，则在船缓慢靠岸的过程中，绳的拉力和船受到的浮力如何变化？ y F浮 F Fy f x F
x
G 答案：绳的拉力逐渐变大，船受到的浮力逐渐减小
如图所示，人的质量为M，物块的质量为m，且 M>m，若不计绳与滑轮的摩擦，则当人拉着绳向右跨出一步后，人和物仍保持静止，则下列说法中正确的是（ BD ） A．地面对人的摩擦力减小 B．地面对人的摩擦力增大 C．人对地面的作用力不变 D．人对地面的作用力增大
例1：如图所示，光滑的小球静止在斜面和竖直放置的木板之间，已知球重为G，斜面的倾角为θ，现使木板沿逆时针方向绕O点缓慢移动，求小球对斜面和挡板的压力
N1
G N2
G N2
解题思路及步骤：（1）明确研究对象。（2）分析物体的受力。
（3）将力平行移动转化为力的矢量三角形。
（4）正确找出力的变化方向。
（ 5 ）根据有向线段的长度变化判断各个力的变化
情况。
如图所示，电灯悬挂于O点，三根绳子的拉力分别为TA、 TB、TC，保持O点的位置不变，绳子的悬点B也不变，则悬点A向上移动的过程中，下列说法正确的是（ D ） A、 TA、TB一直减少； B、 TA一直增大，TB一直减少； TB C、 TA先增大后减少， TB先减少后增大； TA D、TA先减少后增大，TB一直减少；
例2：一轻杆BO，其O端用光滑铰链固定在竖直轻杆 AO上，B端挂一重物，且系一细绳，细绳跨过杆顶 A处的光滑小滑轮，用力F拉住，如图所示。现将细绳缓慢往左拉，使杆BO与杆AO间的夹角θ逐渐减少，则在此过程中，拉力F及杆BO所受压力FN的大小变化情况是( B ) A．FN先减小，后增大 B.FN始终不变 C．F先减小，后增大 D.F始终不变 F FN F

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一端B悬挂一重为G的重物，且B端系有一根轻绳
并绕过定滑轮A，用力F拉绳，开始时∠BCA＞
90°，现使∠BCA缓慢变小，直到杆BC接近竖直
杆AC。此过程中，杆BC所受的力（
）
A.大小不变 B.逐渐增大 A
C.逐渐减小 D.先增大后减小F
C B
mg
例2、如图所示，轻绳长为L，A端固定在天花板上，B端系一个重量为G的小球，小球静止在固定的半径为R的光滑球面上，小球的悬点在球心正上方距离球面最小距离为h，则轻绳对小球的拉力和半球体对小球的支持力分别是多大？
解题思路：
• （1）明确研究对象。（2）分析物体的受力。（3）用力的合成或力的分解作平行四边形（也可简化为矢量三角形）。（4）在合成后的三角形中找到变化的角，画出变化后的三角形
• （5）根据有向线段的长度变化判断各个力的变化情况。
如图所示，电灯悬挂于O点，三根绳子的拉力分别为TA、 TB、TC，保持O点的位置不变，绳子的悬点B也不变，则悬点A向上移动的过程中，下列说法正确的是（ D ）
A.压力随力F增大而增大； B.压力保持不变；
C.静摩擦力随F增大而增大； D.静摩擦力保持不变。
例2.半圆柱体P放在粗糙的水平地面上，其右端有一竖直放置的光
滑挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q，
整个装置处于静止状态，如图所示是这个装置的截面图．现使MN
保持竖直并且缓慢地向右平移，在Q滑落到地面之前，发现P始终
1、对小球受力分析 2、将受力图转化成
矢量三角形
G ＝N ＝T hR R L
T
N
点评：合力大小方向不变，力的
矢量三角形与几何三角形相似。 G
一轻杆BO，其O端用光滑铰链固定在竖直轻杆AO上，
B端挂一重物，且系一细绳，细绳跨过杆顶A处的光滑小滑
轮，用力F拉住，如图所示．现将细绳缓慢往左拉，使杆BO
A．增大B的读数，减小β角
B．减小B的读数，减小β角
C．减小B的读数，增大β角
D．增大B的读数，增大β角
三、相似法
①受力特点：受三个力作用，一个力恒定不变（大小、方向不变）；另两个力可变；合成后与长度三角形相似
例1.如图所示，AC时上端带定滑轮的固定竖直杆，
质量不计的轻杆BC一端通过铰链固定在C点，另
保持静止．则在此过程中，下列说法中正确的是()源自A．MN对Q的弹力逐渐减小
B．地面对P的支持力逐渐增大
C．Q所受的合力逐渐增大
D．地面对P的摩擦力逐渐增大
21
解决动态平衡的步骤
• 正确分析物体动态平衡问题，可分三步进行：
• 1、对物体的初状态进行受力分析。 • 2、在变化过程中，找出不变的物理量。 • 3、应用正交分解法分析物体的受力，列出
与杆AO间的夹角θ逐渐减小，则在此过程中，拉力F及杆BO
所受压力FN的大小变化情况是( A．FN先减小，后增大 C．F先减小，后增大
)B B．FN始终不变 D．F始终不变
二、整体法解决动态问题
如图所示，A、B、C的质量分别为mA、mB、mC，整个系统相对于地处于静止状态，则B对C和地面对C的摩擦力的大小分别为：C
Ａ．mAg，mBg Ｂ．mBg，mAg
Ｃ．mAg，0
Ｄ．mBg，0
B
A
C
如图所示，斜面体放在墙角附近，一个光滑的小球置于竖直墙和斜面之间，若在小球上施加一个竖直向下的力F，小球处于静止。如果稍增大竖直向下的力F，而小球和斜面体都保持静止，关于斜面体对水平地面的压力和静摩擦力的大小的下列说法正确：AC
2．如图，电灯悬挂于两墙之间，更换水平绳 OA使连结点A向上移动而保持O点的位置不变，则A点向上移动时（）
A．绳OA的拉力逐渐增大
B．绳OA的拉力逐渐减小
C．绳OA的拉力先增大后减小
D．绳OA的拉力先减小后增大
A
O
3．如图，用细绳将重球悬挂在竖直光滑墙上，当绳伸长时（）
A．绳的拉力变小，墙对球的弹力变大 B．绳的拉力变小，墙对球的弹力变小 C．绳的拉力变大，墙对球的弹力变小 D．绳的拉力变大，墙对球的弹力变大
平衡关系进行判断。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
23
Thank You
动态平衡问题
1.选择对象：单体和系统
2.受力分析：
隔离对象，分析“受”到的力，要明确“施”力物关注物体状态，判断有无。
3.基本方法：解析法、图解法、三角形相似法正交分解法、合成法、按效果分解
一、动态三角形(图解法）
题型特点：
• （1）物体受三个力。（2）三个力中一个力是恒力，一个力的方向不变，由于第三个力的方向变化，而使该力和方向不变的力的大小发生变化，但二者合力不变。
θ
图解法2：
①受力特点：受三个力作用，一个力恒定不变（大小、方向不变）；一个力大小不变，一个力可变
②方法：合成，
在两个共点力的合成实验中，如图所示，用A、 B两个测力计拉橡皮条的结点D，使其位于 E处，α＋β＜90°，然后保持A的读数不变，当角α由图示位置逐渐减小时，欲使结点仍在E处，可采用的方法是( )
A、 TA、TB一直减少； B、 TA一直增大，TB一直减少； C、 TA先增大后减少，
TB先减少后增大； D、TA先减少后增大，TB一直减少；
1．半圆形支架BAD上悬着两细绳OA和OB，结于圆心O，下悬重为G的物体，使OA绳固定不动，将OB绳的B端沿半圆支架从水平位置缓慢移到竖直位置C的过程中（如图），分析OA绳和OB绳所受力的大小如何变化。
4．如图，一个均质球重为，放在光滑斜面上，倾角为，在斜面上有一光滑的不计厚度的木板挡住球。使之处于静止状态，今使板与斜面的夹角缓慢增大，问：此过程中，球对挡板和球对斜面的压力如何变化？
β α
5．如图，小球被轻质绳系着，斜吊着放在光滑劈上，球质量为，斜面倾角为，在水平向右缓慢推动劈的过程中（） A．绳上张力先增大后减小 B．绳上张力先减小后增大 C．劈对球的支持力减小 D．劈对球的支持力增小