下载文档原格式
输入模拟量与输出数字量的计算公式在我们的电子世界里，输入模拟量与输出数字量之间有着神秘而有趣的关系，这背后藏着一套计算公式。
咱们先来说说啥是输入模拟量。
比如说，温度、压力、声音的强度，这些连续变化的量就是模拟量。
就拿温度来说吧，它可不是一下子从 0 跳到 10 度，而是能在 0 到 10 度之间平滑地变化。
而输出数字量呢，就像是我们在计算机里看到的 0 和 1 组成的数字。
比如说，温度传感器把连续变化的温度转变成计算机能处理的数字信号，这就是从模拟量变成了数字量。
那它们之间的计算公式到底是啥呢？一般来说，常用的公式是：数字量 = （模拟量 - 模拟量下限）×（数字量最大值 - 数字量最小值）÷（模拟量上限 - 模拟量下限） + 数字量最小值咱来举个例子哈。
假设我们有一个温度传感器，它能测量的温度范围是 0 到 100 度（这就是模拟量的范围），而对应的数字量范围是 0到 1023 。
现在测到的温度是 50 度，那按照公式算一下：数字量 = （50 - 0）×（1023 - 0）÷（100 - 0） + 0算出来大概是 511.5 ，因为数字量得是整数，所以就约等于 512 。
还记得我之前参加过一个电子小制作的活动。
我们要做一个能显示环境湿度的小装置。
在这个过程中，就得搞清楚湿度这个模拟量怎么变成能在屏幕上显示的数字量。
当时可把我难坏了，对着那一堆公式和数据，脑袋都大了几圈。
我就不停地测试，调整参数，反复计算。
有好几次都算错了，显示出来的湿度数值完全不对，要么超高，要么超低，就像个调皮的孩子在跟我开玩笑。
但我没放弃，继续琢磨，终于算出了正确的结果。
当看到那个小装置准确地显示出环境湿度的时候，心里那叫一个美呀！这就像是解开了一道神秘的谜题，找到了通往数字世界和现实世界的桥梁。
其实啊，输入模拟量与输出数字量的计算公式在很多地方都有用。
比如在工业自动化控制中，要精确控制机器的运行，就得靠这个公式把各种模拟量转化成数字量，让计算机能明白该怎么做。
模拟量比例换算因为A/D（模/数）、D/A（数/模）转换之间的对应关系，S7-200 SMART CPU内部用数值表示外部的模拟量信号，两者之间有一定的数学关系。
这个关系就是模拟量/数值量的换算关系。
例如，使用一个0 - 20mA的模拟量信号输入，在S7-200 SMART CPU 内部，0 - 20mA对应于数值范围0 - 27648；对于4 - 20mA的信号，对应的内部数值为5530 - 27648。
如果有两个传感器，量程都是0 - 16MPa，但是一个是0 - 20mA输出，另一个是4 - 20mA输出。
它们在相同的压力下，变送的模拟量电流大小不同，在S7-200 SMART内部的数值表示也不同。
显然两者之间存在比例换算关系。
模拟量输出的情况也大致相同。
上面谈到的是0 - 20mA与4 - 20mA之间换算关系，但模拟量转换的目的显然不是在S7-200 SMART CPU中得到一个0 - 27648之类的数值；对于编程和操作人员来说，得到具体的物理量数值（如压力值、流量值），或者对应物理量占量程的百分比数值要更方便，这是换算的最终目标。
通用比例换算公式模拟量的输入/输出都可以用下列的通用换算公式换算：Ov = [(Osh - Osl)*(Iv - Isl)/(Ish - Isl)] + Osl其中：Ov:换算结果Iv:换算对象Osh:换算结果的高限Osl:换算结果的低限Ish:换算对象的高限Isl:换算对象的低限它们之间的关系可以图示如下：图1. 模拟量比例换算关系量程转化指令库为便于用户使用，这里提供了量程转化库，用户可以添加到自己的Micro/WIN编程软件中应用。
模拟量比例换算指令库注意：此指令库/程序的作者和拥有者对于该软件的功能性和兼容性不负任何责任。
使用该软件的风险完全由用户自行承担。
由于它是免费的，所以不提供任何担保，错误纠正和热线支持，用户不必为此联系西门子技术支持与服务部门。
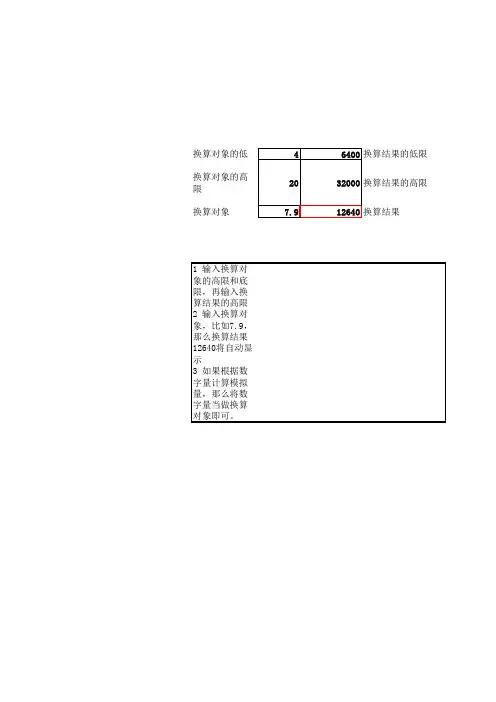
模拟量值和A/D转换值的转换假设模拟量的标准电信号是A0—Am（如：4—20mA），A/D转换后数值为D0—Dm （如：6400—32000），设模拟量的标准电信号是A，A/D转换后的相应数值为D，由于是线性关系，函数关系A＝f（D）可以表示为数学方程：A＝（D－D0）×（Am－A0）／（Dm－D0）＋A0。
根据该方程式，可以方便地根据D值计算出A值。
将该方程式逆变换，得出函数关系D＝f（A）可以表示为数学方程：D＝（A－A0）×（Dm－D0）／（Am－A0）＋D0。
具体举一个实例，以S7-200和4—20mA为例，经A/D转换后，我们得到的数值是6400—32000，即A0＝4，Am＝20，D0＝6400，Dm＝32000，代入公式，得出：A＝（D－6400）×（20－4）／（32000－6400）＋4假设该模拟量与AIW0对应，则当AIW0的值为12800时，相应的模拟电信号是6400×16／25600＋4＝8mA。
又如，某温度传感器，－10—60℃与4—20mA相对应，以T表示温度值， AIW0为PLC模拟量采样值，则根据上式直接代入得出：T=70×（AIW0－6400）／25600－10可以用T直接显示温度值。
模拟量值和A/D转换值的转换理解起来比较困难，该段多读几遍，结合所举例子，就会理解。
为了让您方便地理解，我们再举一个例子：某压力变送器，当压力达到满量程5MPa时，压力变送器的输出电流是20mA， AIW0的数值是32000。
可见，每毫安对应的A/D值为32000/20，测得当压力为0.1MPa时，压力变送器的电流应为4mA，A/D值为（32000/20）×4＝6400。
由此得出，AIW0的数值转换为实际压力值（单位为KPa）的计算公式为：VW0的值＝(AIW0的值－6400)(5000－100)/(32000－6400)＋100（单位：KPa）。
假设模拟量的标准电信号是A0—Am（如：4—20mA），A/D转换后数值为D0—Dm（如：6400—32000），设模拟量的标准电信号是A，A/D转换后的相应数值为D，由于是线性关系，函数关系A＝f（D）可以表示为数学方程：A＝（D－D0）×（Am－A0）／（Dm－D0）＋A0。
根据该方程式，可以方便地根据D值计算出A值。
将该方程式逆换，得出函数关系D＝f（A）可以表示为数学方程：D＝（A－A0）×（Dm－D0）／（Am－A0）＋D0。
具体举一个实例，以S7-200和4—20mA为例，经A/D转换后，我们得到的数值是6400—32000，即A0＝4，Am＝20，D0＝6400，Dm＝32000，代入公式，得出：A＝（D－6400）×（20－4）／（32000－6400）＋4假设该模拟量与AIW0对应，则当AIW0的值为12800时，相应的模拟电信号是6400×16／25600＋4＝8mA。
又如，某温度传感器，－10—60℃与4—20mA相对应，以T表示温度值，AIW0为PLC模拟量采样值，则根据上式直接代入得出：T=70×（AIW0－6400）／25600－10 可以用T 直接显示温度值。
模拟量值和A/D转换值的转换理解起来比较困难，该段多读几遍，结合所举例子，就会理解。
为了让您方便地理解，我们再举一个例子：某压力变送器，当压力达到满量程5MPa时，压力变送器的输出电流是20mA，AIW0的数值是32000。
可见，每毫安对应的A/D值为32000/20，测得当压力为0.1MPa时，压力变送器的电流应为4mA，A/D值为（32000/20）×4＝6400。
由此得出，AIW0的数值转换为实际压力值（单位为KPa）的计算公式为：VW0的值＝(AIW0的值－6400)(5000－100)/(32000－6400)＋100（单位：KPa）编程实例您可以组建一个小的实例系统演示模拟量编程。
模拟量的
输入/输
出都可以
用下列的
通用换算
公式换
算：
假设模拟
量的标准
信号是
A0-Am(如
4-
20mA)，
其中：A/D转换后数值为D0-Dm(如6400-32000)，
Ov: 换算结果设模拟量的标准信号为A，A/D转换后的相应数值为D,由于线性关系，函数关系
A=f(D),可以表示为数学方程式：
Iv: 换算对象
Osh: 换算结果的高限D/A转换：
Osl: 换算结果的低限
A=(D-
D0)*(Am-
A0)/(Dm-
D0)+A0
通用比例换算公式S7-200模拟量/
Ov = [(Osh - Osl)*(Iv - Isl)/(Ish - Isl)] + Osl
根据该方
程式可以
方便的根
据D值算
出A值，
将该方程
式逆变
换，得出
函数关系
D=f(A),
可以表示
为数学方
程式：Ish: 换
算对象的
高限
Isl: 换算对象的低限A/D转换：
D=(A-
A0)*(Dm-D0)/(Am-A0)+D0
A0-Am对应4-
20mA,
D0-Dm对应6400-32000
拟量/数字量换算公式：。
比如有一个压力变送器输入20kp--800kp，输出0—10V信号给PLC，然后PLC把0-10V转换为0-4000数字信号，现在要在PLC程序里实现把20Kp—800KP转换为20-800后直接在触摸屏上显示，可以这样实现，
一种方法调整模拟量增益与偏置，
另外一种方法自己在程序里用公式转换
首先用（4000-0）/(800-20)=5.128,
然后用800乘以5.128等于4102，再用4102-102=4000，
这样就可以得到另外一个公式，以三菱FX为例，当D0为模拟量通道直接写进数范围是0-2000.那么就可以用(D0+K102)/5.128=D1，那么D1就对应20-800，这样就可以直接在触摸屏上显示。
因为在三菱FX-PLC里5.128无法表示，可以把（D0+K102）先乘以K100后在除以K512，这样换算的精度就提高了。
如果还想提高精度可以把（D0+K102）先乘以K1000后，再除以K5128，这样换算的精度就更高了。
这是D0等于0时，0V信号输入，D34等于20。
这是D0等于2000时，5V信号输入，D34等于409。
这是D0等于4000时，10V信号输入，D34等于800。
假设模拟量的标准电信号就是A0—Am(如:4—20mA),A/D转换后数值为D0—Dm(如:6400—32000),设模拟量的标准电信号就是A,A/D转换后的相应数值为D,由于就是线性关系,函数关系A＝f(D)可以表示为数学方程:A＝(D－D0)×(Am－A0)／(Dm－D0)＋A0。
根据该方程式,可以方便地根据D值计算出A值。
将该方程式逆换,得出函数关系D＝f(A)可以表示为数学方程:D＝(A－A0)×(Dm－D0)／(Am－A0)＋D0。
具体举一个实例,以S7-200与4—20mA为例,经A/D转换后,我们得到的数值就是6400—32000,即A0＝4,Am＝20,D0＝6400,Dm＝32000,代入公式,得出:A＝(D－6400)×(20－4)／(32000－6400)＋4假设该模拟量与AIW0对应,则当AIW0的值为12800时,相应的模拟电信号就是6400×16／25600＋4＝8mA。
又如,某温度传感器,－10—60℃与4—20mA相对应,以T表示温度值,AIW0为PLC模拟量采样值,则根据上式直接代入得出:T=70×(AIW0－6400)／25600－10 可以用T 直接显示温度值。
模拟量值与A/D转换值的转换理解起来比较困难,该段多读几遍,结合所举例子,就会理解。
为了让您方便地理解,我们再举一个例子:某压力变送器,当压力达到满量程5MPa时,压力变送器的输出电流就是20mA,AIW0的数值就是32000。
可见,每毫安对应的A/D值为32000/20,测得当压力为0、1MPa时,压力变送器的电流应为4mA,A/D 值为(32000/20)×4＝6400。
由此得出,AIW0的数值转换为实际压力值(单位为KPa)的计算公式为:VW0的值＝(AIW0的值－6400)(5000－100)/(32000－6400)＋100 (单位:KPa)编程实例您可以组建一个小的实例系统演示模拟量编程。
教你几步搞定模拟量计算在工程设计和控制系统中，经常需要对模拟量进行计算以满足工程需求。
模拟量指连续变化的物理量，如电压、电流以及温度等。
在本文中，我们将介绍几个简单的步骤，以帮助你更好地理解模拟量计算。
步骤一：单位转换在进行模拟量计算之前，首先要确认各个物理量的单位，以确保计算的准确性。
下面是一些常见的模拟量单位：•电压：伏特（V）•电流：安培（A）•电阻：欧姆（Ω）•温度：摄氏度（℃）或华氏度（℉）需要注意的是，在进行计算时，要将所有的单位转换成国际标准单位。
例如，摄氏度到开尔文（K）的转换公式为 K = ℃ + 273.15。
步骤二：信号强度转换模拟信号的强度通常采用电压、电流或功率来表示。
在进行模拟量计算之前，需要将这些强度换算成其他单位，以便进行计算。
例如，将电流转换为功率的公式为：P = I * V其中，P表示功率，I表示电流，V表示电压。
需要注意的是，在进行信号强度转换时，要注意信号的极性和方向，以免出现误差。
步骤三：标准化对于不同的模拟量信号，通常需要将其标准化后才能进行有效的比较和计算。
标准化的目的是将不同物理量之间的差异量化为一个统一的量纲，以便进行比较。
例如，将温度进行标准化的方法是将其转换为摄氏度或开尔文。
另一个常用的标准化方法是百分比，将实际值除以最大值，然后将结果乘以100。
步骤四：模拟量计算经过前面三步的准备工作，现在可以进行模拟量计算了。
模拟量计算方式多种多样，下面是几个常见的方法：算术平均值算术平均值可以简单地通过将所有值相加然后除以总数来计算。
这个方法广泛应用于各种数据分析中，特别是在控制系统中。
例如，计算三个数据点的平均温度：(20℃+25℃+30℃)/3=25℃加权平均值加权平均值是指根据每个数据点的权重来计算平均值。
权重表示每个数据点的重要性。
例如，计算三个数据点的加权平均温度：(20℃*2+25℃*3+30℃*5)/(2+3+5)=28℃标准差标准差是对数据的离散程度测量的一种方法。
因为A/D（模/数）、（D/A）数/模转换之间的对应关系，S7-200 CPU 内部用数值表示外部的模拟量信号，两者之间有一定的数学关系。
这个关系就是模拟量/数值量的换算关系。
例如，使用一个0 - 20mA的模拟量信号输入，在S7-200 CPU内部，0 - 20mA对应于数值范围0 - 32000；对于4 - 20mA的信号，对应的内部数值为6400 - 32000。
如果有两个传感器，量程都是0 - 16MPa，但是一个是0 - 20mA 输出，另一个是4 - 20mA输出。
它们在相同的压力下，变送的模拟量电流大小不同，在S7-200内部的数值表示也不同。
显然两者之间存在比例换算关系。
模拟量输出的情况也大致相同。
上面谈到的是0 - 20mA与4 - 20mA之间换算关系，但模拟量转换的目的显然不是在S7-200 CPU中得到一个0 - 32000之类的数值；对于编程和操作人员来说，得到具体的物理量数值（如压力值、流量值），或者对应物理量占量程的百分比数值要更方便，这是换算的最终目标。
如果使用编程软件Micro/WIN32中的PID Wizard（PID向导）生成PID功能子程序，就不必进行0 - 20mA与4 - 20mA信号之间的换算，只需进行简单的设置。
通用比例换算公式模拟量的输入/输出都可以用下列的通用换算公式换算：Ov = [(Osh - Osl)*(Iv - Isl)/(Ish - Isl)] + Osl其中：Ov:换算结果Iv:换算对象O sh:换算结果的高限O sl:换算结果的低限I sh:换算对象的高限I sl:换算对象的低限它们之间的关系可以图示如下：图1. 模拟量比例换算关系实用指令库在Step7 - Micro/WIN Programming Tips（Micro/WIN编程技巧中）的Tip38就是关于如何实现上述转换的例程。
为便于使用，现已将其导出成为”自定义指令库“，可以添加到自己的Micro/WIN编程软件中应用。
