高等数学(同济大学版)第三章练习(含答案)

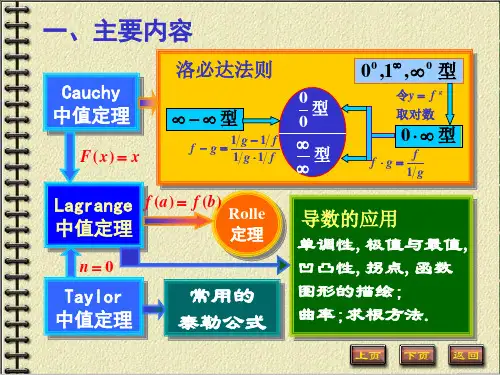
第三章 微分中值定理与导数的应用一、要求：1、罗尔定理，拉格朗日定理应用；2、洛必达法则；3、函数单调性、极值、最值、凹凸性、拐点的判断，函数图形的描绘；4、简单不等式证明；5、最值在实际问题中的应用。

二、练习1. 在区间 [ 1,1] 上满足罗尔定理条件的函数是 ().A.1 B.f ( x ) | x | C. f ( x) 1 x 2D. f ( x ) x22 x 1.f ( x)x 22. 函数 f ( x) arctan x 在 [ 0 ,1] 上满足拉格郎日中值定理的值是 ().A.4B.41C. 1D. 4.11 3.4设函数 f ( x ) ( x 1)( x2)( x 3)，则方程 f ( x )0 有个零点，这些零点所在的范围是；.3. 设函数 f ( x ) ( x 1)( x 2)( x 3)，则方程 f ( x )0 有个零点，这些零点所在的范围是.4. 函数 f ( x ) ln xx2在(0,) 内的零点的个数为.e5. 曲线6. 函数yxe x 的拐点 ，凹区间，凸区间.yln x1x 2的单调区间.7. 曲线 f ( x) e x的渐近线为.x 18. 计算：5 x 4x11(12（2） lim (cos x )（1） limx 1xx) （3） limtan 2 xx1xe 1x 0arctan x x(1 x 2 )1 / 31 ；1（ 4） lim ；（5） lim（6） lim (cscx ) ；x 0x ln(1 2 x 2 )xcosx1x 0x（ 7） lim x 3 (sin 11 sin2 ) ；（ ） lim (tanx )2 x；（ 9） limx；exx2x8x ln xx29. 证明 2 arctanxarcsin2 xx1 .21 x10. 证明方程x5x10 在区间( 1, 0)内有且只有一个实根.11. 证明多项式f x3 3 x a 在0,1上不可能有两个零点 .x12. 证明：当0x时， x sin x 22x13.证明：当x0时，1x2arctan x xx14. 设 f x32bx在 x 1 处有极值-2，试确定系数 a , b ，并求x axy f x 的所有极值点与拐点.15. 求内接于椭圆x2y2221 而面积最大的矩形的各边之长.a b16.由直线 y0,x8及抛物线 y x2围成一个曲边三角形 ,在曲边 y x2上求一点 , 使曲线在该点处的切线与直线y0 及 x 8 所围成的三角形面积最大.17.描绘 (1)y 3 x2，(2) y21的图形 .2( x1) ( x 1) 2( x 1)18.要做一个容积为 2 的密闭圆柱形罐头筒，问半径和筒高如何确定才能使所用材料最省？19．要造一个长方体无盖蓄水池，其容积为500 立方米，底面为正方形。

习题3-1 1.验证罗尔定理对函数y =ln sin x 在区间]65,6[p p 上的正确性.解因为y =ln ln sin sin x 在区间]65,6[p p 上连续, 在)65,6(p p 内可导, 且)65()6(pp y y =, 所以由罗尔定理知, 至少存在一点)65,6(pp x Î, 使得y ¢(x )=cot x =0.由y ¢(x )=cot x =0得)65,6(2pp p Î.因此确有)65,6(2pp p x Î=, 使y ¢(x )=cot x =0.2.验证拉格朗日中值定理对函数y =4x 3-5x 2+x -2在区间[0, 1]上的正确性.解因为y =4x 3-5x 2+x -2在区间[0, 1]上连续, 在(0, 1)内可导, 由拉格朗日中值定理知, 至少存在一点x Î(0, 1), 使001)0()1()(=--=¢yy y x .由y ¢(x )=12x2-10x +1=0得)1,0(12135α=x .因此确有)1,0(12135α=x , 使01)0()1()(--=¢y y y x .3.对函数f (x )=sin x 及F (x )=x +cos x 在区间]2,0[p 上验证柯西中值定理的正确性.解因为f (x )=sin x 及F (x )=x +cos x 在区间]2,0[p 上连续, 在)2,0(p 可导, 且F ¢(x )=1-sin x 在)2,0(p 内不为0, 所以由柯西中值定理知至少存在一点)2,0(px Î, 使得)()()0()2()0()2(x x p p F f F F f f ¢¢=--.令)0()2()0()2()()(F F f f x F x f --=¢¢p p , 即22sin 1cos -=-p x x .化简得14)2(8sin 2-+-=p x . 易证114)2(802<-+-<p , 所以14)2(8sin 2-+-=p x 在)2,0(p 内有解, 即确实存在)2,0(px Î, 使得)()()0()2()0()2(x x p p F f F F f f ¢¢=--.4. 试证明对函数y =px 2+qx +r 应用拉格朗日中值定理时所求得的点x 总是位于区间的正中间.证明证明证明 因为函数y =px 2+qx +r 在闭区间[a , b ]上连续, 在开区间(a , b )内可导, 由拉格朗日中值定理, 至少存在一点x Î(a , b ), 使得y (b )-y (a )=y ¢(x )(b -a ), 即 (pb 2+qb +r )-(pa 2+qa +r )=(2p x +q )(b -a ). 化间上式得化间上式得p (b -a )(b +a )=2p x (b -a ),故2b a +=x .5. 不用求出函数f (x )=(x -1)(x -2)(x -3)(x -4)的导数，说明方程f ¢(x )=0有几个实根, 并指出它们所在的区间.解 由于f (x )在[1, 2]上连续, 在(1, 2)内可导, 且f (1)=f (2)=0, 所以由罗尔定理可知, 存在x 1Î(1, 2), 使f ¢(x 1)=0. 同理存在x 2Î(2, 3), 使f ¢(x 2)=0; 存在x 3Î(3, 4), 使f ¢(x 3)=0. 显然x 1、x 2、x 3都是方程f ¢(x )=0的根. 注意到方程f ¢(x )=0是三次方程, 它至多能有三个实根, 现已发现它的三个实根, 故它们也就是方程f ¢(x )=0的全部根. 6. 证明恒等式: 2arccos arcsi n p=+x x (-1£x £1).证明证明 设f (x )= arcsin x +arccos x . 因为因为 01111)(22º---=¢xxx f ,所以f (x )ºC , 其中C 是一常数. 因此2arccos arcsin )0()(p=+==x x f x f , 即2arccos arcsin p=+x x .7. 若方程a 0x n+a 1x n -1+ × × × + a n -1x =0有一个正根x 0, 证明方程证明方程 a 0nx n -1+a 1(n -1)x n -2 + × × × +a n -1 =0 必有一个小于x 0的正根.证明证明 设F (x )=a 0x n +a 1x n -1+ × × × + a n -1x , 由于F (x )在[0, x 0]上连续, 在(0, x 0)内可导, 且F (0)=F (x 0)=0, 根据罗尔定理, 至少存在一点x Î(0, x 0), 使F ¢(x )=0, 即方程即方程 a 0nx n -1+a 1(n -1)xn -2 + × × × +a n -1 =0 必有一个小于x 0的正根.8. 若函数f (x )在(a , b )内具有二阶导数, 且f (x 1)=f (x 2)=f (x 3), 其中a <x 1<x 2<x 3<b , 证明: 在(x 1, x 3)内至少有一点x , 使得f ¢¢(x )=0. 证明证明 由于f (x )在[x 1, x 2]上连续, 在(x 1, x 2)内可导, 且f (x 1)=f (x 2), 根据罗尔定理, 至少存在一点x 1Î(x 1, x 2), 使f ¢(x 1)=0. 同理存在一点x 2Î(x 2, x 3), 使f ¢(x 2)=0. 又由于f ¢(x )在[x 1, x 2]上连续, 在(x 1, x 2)内可导, 且f ¢(x 1)=f ¢(x 2)=0, 根据罗尔定理, 至少存在一点x Î(x 1, x 2)Ì(x 1, x 3), 使f ¢¢(x )=0. 9. 设a >b >0, n >1, 证明:nb n -1(a -b )<a n-b n<na n -1(a -b ) .证明证明 设f (x )=x n, 则f (x )在[b , a ]上连续, 在(b , a )内可导, 由拉格朗日中值定理, 存在x Î(b , a ), , 使 f (a )-f (b )=f ¢(x )(a -b ), 即a n -b n =n x n -1(a -b ).因为因为 nb n -1(a -b )<n x n -1(a -b )< na n -1(a -b ),所以所以 nb n -1(a -b )<a n -b n < na n -1(a -b ) . 10. 设a >b >0, 证明:bb a b a a b a -<<-ln . 证明证明 设f (x )=ln x , 则f (x )在区间[b , a ]上连续, 在区间(b , a )内可导, 由拉格朗日中值定理, 存在x Î(b , a ), , 使f (a )-f (b )=f ¢(x )(a -b ), 即)(1ln ln b a b a -=-x.因为b <x <a , 所以所以)(1ln ln )(1b a b b a b a a -<-<-, 即bb a b a a b a -<<-ln . 11. 证明下列不等式:(1)|arctan a -arctan b |£|a -b |; (2)当x >1时, e x>e ×x . 证明证明 (1)设f (x )=arctan x , 则f (x )在[a , b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在x Î(a , b ), 使f (b )-f (a )=f ¢(x )(b -a ), 即)(11arctan arctan 2ab a b -+=-x,所以||||11|arctan arctan |2a b a b a b -£-+=-x, 即|arctan a -arctan b |£|a -b |. (2)设f (x )=e x, 则f (x )在区间[1, x ]上连续, 在区间(1, x )内可导, 由拉格朗日中值定理, 存在x Î(1, x ), 使 f (x )-f (1)=f ¢(x )(x -1), 即 e x -e =e x(x -1). 因为x >1, 所以所以e x -e =e x (x -1)>e (x -1), 即e x >e ×x .12. 证明方程x 5+x -1=0只有一个正根.证明证明 设f (x )=x 5+x -1, 则f (x )是[0, +¥)内的连续函数.因为f (0)=-1, f (1)=1, f (0)f (1)<0, 所以函数在(0, 1)内至少有一个零点, 即x 5+x -1=0至少有一个正根.假如方程至少有两个正根, 则由罗尔定理, f ¢(x )存在零点, 但f ¢(x )=5x 4+1¹0, 矛盾. 这说明方程只能有一个正根.13. 设f (x )、g (x )在[a ,b ]上连续, 在(a , b )内可导, 证明在(a , b )内有一点x , 使 )()()()()()()()()(xx g a g f a f a b b g a g b f a f ¢¢-=.解 设)()()()()(x g a g x f a f x =j , 则j (x )在[a ,b ]上连续, 在(a , b )内可导, 由拉格朗日中值定理, 存在x Î(a ,b ), 使 j (b )-j (a )=j ¢(x )(b -a ),即 úûùêë颢+¢¢-=-)()()()()(])([)(])([)()()()()()()()()(x x x x g a g f a f g a g f a f a b a g a g a f a f b g a g b f a f . 因此因此 )()()()()()()()()(xx g a g f a f a b b g a g b f a f ¢¢-=.14. 证明: 若函数.f (x )在(-¥, +¥)内满足关系式f ¢(x )=f (x ), 且f (0)=1则f (x )=e x. 证明证明 令x ex f x )()(=j , 则在(-¥, +¥)内有内有0)()()()()(2222º-=-¢=¢xxx x eex f e x f ee xf e x f x j , 所以在(-¥, +¥)内j (x )为常数.因此j (x )=j (0)=1, 从而f (x )=e x. 15. 设函数y =f (x )在x =0的某邻域内具有n 阶导数, 且f (0)=f ¢(0)= × × × =f (n -1)(0)=0, 试用柯西中值定理证明: !)()()(n x fx x f n n q =(0<q <1).证明证明 根据柯西中值定理 111)(0)0()()(-¢=--=n nn f x f x f xx f x x (x 1介于0与x 之间),2221111111)1()(0)0()()(-----¢¢=×-¢-¢=¢n n n n n n f n n f f n f x x x x x x (x 2介于0与x 1之间),3332222222)2)(1()(0)1()1()0()()1()(------¢¢¢=×---¢¢-¢¢=-¢¢n n n n n n n f n n n n f f n n f x x x x x x (x 3介于0与x 2之间), 依次下去可得依次下去可得 !)(02)1(2 )1()0()(2)1()()(1)1(1)1(11)1(n fn n n n ffn n fn n n n n n n n n x x xx x=××××--××××--=××××--------(x n 介于0与x n -1之间), 所以!)()()(n fxx f n n n x =由于x n 可以表示为x n =qx (0<q <1), 所以!)()()(n x fx x f n n q = (0<q <1).习题3-2 1. 用洛必达法则求下列极限:解 (1)111lim 111lim )1ln(lim 0=+=+=+®®®xxxx x x x . (2)2cos limsin lim=+=--®-®xeex ee xxx xxx .(3)a x a x a x ax a x cos 1cos lim sin sin lim ==--®®.(4)535sec 53cos 3lim 5tan 3sin lim2-==®®xx x xx x pp . (5)812csclim 41)2()2(2cot lim )2(sin ln lim 22222-=---=-×-=-®®®xx x x x x x x pppp p .(6)nm n m n m ax nnm m ax anm namx nxmx axa x -----®®===--1111lim lim .(7)177sec22sec lim 277tan 2tan lim 2722sec2tan 177sec 7tan 1lim 2tan ln 7tan ln lim220220=××==××××=++®®++®®+®+®x x xx x xx x xxx x x x .(8))sin (cos 23)3sin (3cos 2lim 31cos 3cos lim 3133sec sec lim 3tan tan lim 22222222x x x x x x x x x x x x x x -×-==×=®®®®pp p p3sin 3sin 3limcos 3cos lim22=---=-=®®xx xx x x pp.(9)122lim212lim1lim11)1(111limcot arc )11ln(lim 2222==+=++=+-×+=++¥®+¥®+¥®+¥®+¥®x x x x x xx xx x x xxxx.(10)xxxx x xx x x x x 220222cos 1lim cos1)1ln(cos lim cos sec )1ln(lim -=-+=-+®®®®(注: cos x ×ln(1+x 2)~x 2) 1sin lim )sin (cos 22lim 0==--=®®xx x x xx x .(11)2122sec1lim2tan lim 2cot lim2=×==®®®®x xx x x x xx .(12)+¥====+¥®+¥®®®1lim lim 1limlim 2101222ttttxx xx ete xee x (注: 当x ®0时, +¥®=21xt).(13)2121lim 11lim 1112lim 12121-=-=--=÷øöçèæ---®®®x x x x x x x x .(14)因为)1ln(lim )1(lim x a x x x x e xa +¥®¥®=+,而aa ax ax xxa xa xxa xa x x x x x x ==+=--×+=+=+¥®¥®¥®¥®¥®1limlim1)(11lim1)1ln(lim)1(ln(lim 22,所以所以ax a x x xx ee xa==++¥®¥®)1l n (lim )1(lim ..(15)因为xx x xxe xln sin 0sin 0lim lim +®+®=, ,而0cos sinlim cot csc 1lim csc ln lim ln sin lim 2=-=×-==+®+®+®+®xx xxx x x xx x x x x x ,所以所以1lim lim 0ln sin 0sin 0===+®+®ee x xx x xx .(16)因为xx xx exln tan tan 0)1(lim -+®=, ,而sinlim csc1lim cot ln lim ln tan lim 22000=-=-==+®+®+®+®xxxx x x x x x x x x ,所以所以1lim )1(lim 0ln tan 0tan 0===-+®+®e exx x x xx .2. 验证极限xxx x sin lim +¥®存在, 但不能用洛必达法则得出.解1)s i n 1(lim sin lim =+=+¥®¥®xx xxx xx , 极限xxx x si n lim +¥®是存在的.但)cos 1(lim 1cos 1lim )()sin (lim x xx x x xxx +=+=¢¢+¥®¥®¥®不存在, 不能用洛必达法则. 3. 验证极限xx x x sin 1sin lim2®存在, 但不能用洛必达法则得出. 解011sinsin limsin 1sinlim2=×=×=®®xx xx x x x x x , 极限xxx x sin 1sinlim2®是存在的.但xxxx x xx x x cos 1cos1sin2lim )(sin )1sin(lim 02-=¢¢®®®不存在, 不能用洛必达法则.4. 讨论函数ïïîïïíì£>+=-0 0 ])1([)(2111x e x ex x f x x在点x =0处的连续性. 解21)0(-=ef , )0(lim )(lim 212100f e ex f x x ===---®-®, ,因为因为]1)1ln(1[101100lim ])1([lim )(lim -+-®-®+®=+=x xx x xxx x e ex x f , ,而21)1(21lim 2111lim )1ln(lim ]1)1ln(1[1lim 00200-=+-=-+=-+=-++®+®+®+®x x x xx x x x x x x x x ,所以所以)0(lim ])1([lim )(lim 21]1)1ln(1[101100f e e ex x f x xx x xxx x ===+=--+-®-®+®.因此f (x )在点x =0处连续.习题3-3 1. 按(x -4)的幂展开多项式x 4-5x 3+x 2-3x +4. 解 因为f (4)=-56, f ¢(4)=(4x 3-15x 2+2x -3)|x =4=21,f ¢¢(4)=(12x 2-30x +2)|x =4=74, f ¢¢¢(4)=(24x -30)|x =4=66,f (4)(4)=24,所以按(x -4)的幂展开的多项式为的幂展开的多项式为435234+-+-x x x x 4)4(32)4(!4)4()4(!3)4()4(!2)4()4)(4()4(-+-¢¢¢+-¢¢+-¢+=x fx f x f x f f=-56+21(x -4)+37(x -4)2+11(x -4)3+(x -4)4. 2. 应用麦克劳林公式, 按x 幂展开函数f (x )=(x 2-3x +1)3. 解 因为因为 f ¢(x )=3(x 2-3x +1)2(2x -3),f ¢¢(x )=6(x 2-3x +1)(2x -3)2+6(x 2-3x +1)2=30(x 2-3x +1)(x 2-3x +2),f ¢¢¢(x )=30(2x -3)(x 2-3x +2)+30(x 2-3x +1)(2x -3)=30(2x -3)(2x 2-6x +3), f (4)(x )=60(2x 2-6x +3)+30(2x -3)(4x -6)=360(x 2-3x +2),f (5)(x )=360(2x -3), f (6)(x )=720;f (0)=1, f ¢(0)=-9, f ¢¢(0)=60, f ¢¢¢(0)=-270, f (4)(0)=720, f (5)(0)=-1080, f (6)(0)=720, 所以所以6)6(5)5(4)4(32!6)0(!5)0(!4)0(!3)0(!2)0()0()0()(xfx fx fx f x f x f f x f +++¢¢¢+¢¢+¢+==1-9x +30x 3-45x 3+30x 4-9x 5+x 6.3. 求函数x x f =)(按(x -4)的幂展开的带有拉格朗日型余项的3阶泰勒公式. 解 因为24)4(==f 4121)4(421==¢=-x xf , 32141)4(423-=-=¢¢=-x xf ,328383)4(425×==¢¢¢=-x xf , 27)4(1615)(--=xx f,所以所以 4)4(32)4(!4)()4(!3)4()4(!2)4()4)(4()4(-+-¢¢¢+-¢¢+-¢+=x fx f x f x f f x x4732)4()]4(4[1615!41)4(5121)4(641)4(412--+×--+---+=x x x x x q(0<q <1).4. 求函数f (x )=ln x 按(x -2)的幂展开的带有佩亚诺型余项的n 阶泰勒公式. 解 因为因为f ¢(x )=x -1, f ¢¢(x )=(-1)x -2, f ¢¢¢(x )=(-1)(-2)x -3, × × × , nn nnxn x n x f )!1()1()1( )2)(1()(1)(--=+-×××--=--;kk kk f 2)!1()1()2(1)(--=-(k =1, 2, × × ×, n +1) 所以所以])2[()2(!)2( )2(!3)2()2(!2)2()2)(2()2(ln )(32nn n x o x n fx f x f x f f x -+-+×××+-¢¢¢+-¢¢+-¢+=])2[()2(2)1( )2(231)2(221)2(212ln 13322nnnn x o x n x x x -+-×-+×××--×+-×--+=-.5. 求函数xxf 1)(=按(x +1)的幂展开的带有拉格朗日型余项的n 阶泰勒公式.解 因为因为f (x )=x -1, f ¢(x )=(-1)x -2, f ¢¢(x )=(-1)(-2)x -3, × × × ,1)1()(!)1()()2)(1()(++--=-×××--=n nn n xn x n x f;!)1(!)1()1(1)(k k fk kk -=--=-+(k =1, 2, × × ×, n ),所以所以 )1(!3)1()1(!2)1()1)(1()1(132×××++-¢¢¢++-¢¢++-¢+-=x f x f x f f x1)1()()1()!1()()1(!)1(++++++-+n n nn x n fx n fx12132)1()]1(1[)1(])1()1()1()1(1[++++++--+++×××+++++++-=n n n n x x x x x x q (0<q <1). 6. 求函数f (x )=tan x 的带有拉格朗日型余项的3阶麦克劳林公式. 解 因为因为f ¢(x )=sec 2x , f ¢¢(x )=2sec x ×sec x ×tan x =2sec 2x ×tan x , f ¢¢¢(x )=4sec x ×sec x ×tan 2x +2sec 4x =4sec 2x ×tan 2x +2sec 4x , f (4)(x )=8sec 2x ×tan 3x +8sec 4x ×tan x +8sec 4x ×tan x xx x 52cos)2(sinsin 8+=;f (0)=0, f ¢(0)=1, f ¢¢(0)=0, f ¢¢¢(0)=2, 所以所以 4523)(c o s 3]2)()[s i n s i n (31t a n x x x x x x x q q q +++=(0<q <1).7. 求函数f (x )=xe x的带有佩亚诺型余项的n 阶麦克劳林公式. 解 因为因为 f ¢(x )=e x +x e x , f ¢¢(x )=e x +e x +x e x =2e x +x e x, f ¢¢¢(x )=2e x +e x +x e x =3e x +x e x , × × ×,f (n )(x )=ne x +xe x ; f (k )(0)=k (k =1, 2, × × ×, n ),所以所以 )(!)0( !3)0(!2)0()0()0()(32nn n xx o x n fx f x f x f f xe ++××××+¢¢¢+¢¢+¢+=)()!1(1!2132n n x o x n x x x +-×××+++=.8. 验证当210££x 时, 按公式62132xx x e x +++»计算e x的近似值时, 所产生的误差小于0.01, 并求e 的近似值, 使误差小于0.01.解 因为公式62132xxx e x+++»右端为e x的三阶麦克劳林公式, 其余项为其余项为43!4)(xex R x=,所以当210££x 时，按公式62132xxx e x+++»计算e x的误差01.00045.0)21(!43|!4||)(|42143<»£=x ex R x.645.1)21(61)21(212113221»×+×++»=e e . 9. 应用三阶泰勒公式求下列各数的近似值, 并估计误差: (1)330;(2)sin 18°. 解 (1)设3)(x x f =, 则f (x )在x 0=27点展开成三阶泰勒公式为点展开成三阶泰勒公式为2353233)27)(2792(!21)27(273127)(-×-×+-×+==--x x x x f4311338)27)(8180(!41)27)(272710(!31--×+-××+--x x x(x 介于27与x 之间).于是于是 33823532333)272710(!313)2792(!21327312730×××+××-×+××+»---10724.3)3531311(31063»+-+»,其误差为其误差为5114311431131088.13!4803278180!41|3)8180(!41||)30(|---´=×=×××<×-×=x R .(2) 已知已知 43!4s i n!31s i n x x x x x +-=(x 介于0与x 之间),所以所以 sin 18°3090.0)10(!311010sin 3»-»=p p p ,其误差为44431003.2)10(!46sin|)10(!4sin ||)10(|-´=<=p pp x pR .10. 利用泰勒公式求下列极限: (1))23(lim 434323x x xx x --++¥®;(2))]1ln([cos lim 222x x x ex xx -+--®;(3)222sin )(cos 1211lim 2xe x xx xx -+-+®.解 (1)ttt xx xx x x x t x x 43434343232131lim 12131lim )23(lim --+=--+=--++®+¥®+¥®.因为)(1313to t t ++=+,)(211214t o t t +-=-, 所以所以23])(23[lim )](211[)](1[lim )23(lim 00434323=+=+--++=--++®+®+¥®t t o tt o t t o t x x x x t t x .(2)])1ln(1[)](41!21211[)](!41!211[lim )]1ln([cos lim 13442442222x x xx x x x o x x x o x x x x x ex -++×+--++-=-+-®-®010)1l n (1)(121lim 1134=+=-++-=-®ex xx o x xx .(3)244244244222220))](!211())(!41!211[()](!43!211[211lim sin )(cos 1211lim 2xx o x x x o x x x o x x x xe x xx x xx +++-++-+-+-+=-+-+®®12123!43)(241123)(!43lim )(241123)(!43lim 2424404264440-=-=+--+=×+--+=®®xx o x x x o x o x x x x o x x x .习题3-4 1. 判定函数f (x )=arctan x -x 单调性. 解 因为011111)(22£+-=-+=¢xxx f , 且仅当x =0时等号成立, 所以f (x )在(-¥, +¥)内单调减少.2. 判定函数f (x )=x +cos x (0£x £2p )的单调性. 解 因为f ¢(x )=1-sin x ³0, 所以f (x )=x +cos x 在[0, 2p ]上单调增加.3. 确定下列函数的单调区间: (1) y =2x 3-6x 2-18x -7; (2)x x y 82+=(x >0); (3)xx x y 6941023+-=;(4))1ln(2x x y ++=; (5) y =(x -1)(x +1)3; (6))0.())(2(32>--=a x a a x y ; (7) y =x n e -x(n >0, x ³0);(8)y =x +|sin 2x |. 解 (1) y ¢=6x 2-12x -18=6(x -3)(x +1)=0, 令y ¢=0得驻点x 1=-1, x 2=3. 列表得列表得可见函数在(-¥, -1]和[3, +¥)内单调增加, 在[-1, 3]内单调减少. (2) 0)2)(2(28222=+-=-=¢xx x xy ,令y ¢=0得驻点x 1=2, x 2=-2(舍去).因为当x >2时, y >0; 当0<x <2时, y ¢<0, 所以函数在(0, 2]内单调减少, 在[2, +¥)内单调x (-¥, -1) -1 (-1, 3) 3 (3, +¥) y ¢ + 0 - 0 +y ↗ ↘ ↗增加. (3)223)694()1)(12(60x x x x x y +----=¢, 令y ¢=0得驻点211=x ,x 2=1, 不可导点为x =0. 列表得列表得x (-¥, 0) 0 (0, 21) 21 (21, 1) 1 (1, +¥) y ¢- 不存在不存在-0 + 0 - y↘↘０↗↘可见函数在(-¥, 0), ]21,0(, [1, +¥)内单调减少, 在]1,21[上单调增加. (4)因为011)1221(11222>+=++++=¢xxx xx y , 所以函数在(-¥, +¥)内单调增加.(5) y ¢=(x +1)3+3(x -1)(x +1)22)1)(21(4+-=x x . 因为当21<x 时, y ¢<0; 当21>x 时, y ¢>0, 所以函数在]21 ,(-¥内单调减少, 在) ,21[¥+内单调增加. (6)32)()2(3)32(x a a x a x y ----=¢, 驻点为321a x =, 不可导点为22a x =, x 3=a .列表得列表得x )2,(a -¥2a)32 ,2(a a32a ),32(a aa (a , +¥) y ¢ + 不存在不存在 + 0 - 不存在不存在 +y↗↗↘↗可见函数在)2 ,(a -¥, ]32 ,2(aa , (a , +¥)内单调增加, 在) ,32[a a 内单调减少.(7)y ¢=e -x x n -1(n -x ), 驻点为x =n . 因为当0<x <n 时,y ¢>0; 当x >n 时, y ¢<0, 所以函数在[0, n ]上单调增加, 在[n , +¥)内单调减少.(8)ïïîïïíì+<<+-+££+=p p p p p p p k x k x x k x k x x y 2 2sin 2 2sin (k =0, ±1, ±2, × × ×),ïïîïïíì+<<+-+££+=¢pp p p p p p k x k x k x k x y 2 2cos 212 2cos 21(k =0, ±1, ±2, × × ×).y ¢是以p 为周期的函数, 在[0, p ]内令y ¢=0, 得驻点21p =x , 652p =x , 不可导点为23p =x .列表得列表得x )3,0(p3p)2,3(p p2p)65 ,2(p p65p ) ,65(p py ¢ + 0 - 不存在不存在 + 0 - y↗↘ ↗↘根据函数在[0, p ]上的单调性及y ¢在(-¥, +¥)的周期性可知函数在]32,2[ppp+k k 上单调增加,在]22 ,32[pp p p++k k 上单调减少(k =0, ±1, ±2, × × ×). 4. 证明下列不等式: (1)当x >0时, xx +>+1211;(2)当x >0时, 221)1ln(1x x x x +>+++; (3)当20p<<x 时, sin x +tan x >2x ; (4)当20p<<x 时, 331tan x x x +>;(5)当x >4时, 2x>x 2; 证明证明 (1)设xx x f +-+=1211)(, 则f (x )在[0, +¥)内是连续的. 因为因为x x f +-=¢12121)(01211>+-+=x x ,所以f (x )在(0, +¥)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即 01211>+-+x x ,也就是也就是 x x +>+1211.(2)设221)1ln(1)(x x x x x f +-+++=, 则f (x )在[0, +¥)内是连续的. 因为因为0)1l n (1)11(11)1l n ()(22222>++=+-++×++×+++=¢x x xx xx xx x x x x f , 所以f (x )在(0, +¥)内是单调增加的, 从而当x >0时f (x )>f (0)=0, 即01)1l n (122>+-+++x x xx , 也就是也就是 221)1l n (1x x xx +>+++. (3)设f (x )=sin x +tan x -2x , 则f (x )在)2 ,0[p内连续,f ¢(x )=cos x +sec 2x -2xx x x 22cos ]cos )1)[(cos 1(cos ---=.因为在)2,0(p 内cos x -1<0, cos 2x -1<0,-cos x <0, 所以f ¢(x )>0, 从而f (x )在)2,0(p 内单调增加, 因此当20p<<x 时,f (x )>f (0)=0, 即 sin x +tan x -2x >0, 也就是也就是 sin x +tan x >2x . (4)设331tan )(x x x x f --=, 则f (x )在)2 ,0[p内连续,))(t a n (t a nt a n 1s e c )(2222x x x x x x x x x f +-=-=--=¢. 因为当20p<<x 时, tan x >x , tan x +x >0, 所以f ¢(x )在)2,0(p 内单调增加, 因此当20p<<x 时,f (x )>f (0)=0, 即 031t a n 3>--x x x ,也就是也就是 231tan x x x +>.(5)设f (x )=x ln2-2ln x , 则f (x )在[4, +¥)内连续, 因为因为 0422ln 224ln 22ln )(=->-=-=¢e x x x f ,所以当x >4时, f ¢(x )>0, 即f (x )内单调增加.因此当x >4时, f (x )>f (4)=0, 即x ln2-2ln x >0, 也就是也就是2x>x 2. 5. 讨论方程ln x =ax (其中a >0)有几个实根？有几个实根？解 设f (x )=ln x -ax . 则f (x )在(0, +¥)内连续, xax a xx f -=-=¢11)(, 驻点为ax 1=.因为当a x 10<<时, f ¢(x )>0, 所以f (x )在)1,0(a内单调增加; 当ax 1>时, f ¢(x )<0, 所以f (x )在) ,1(¥+a内单调减少. 又因为当x ®0及x ®+¥时, f (x )®-¥, 所以如果011ln )1(>-=aa f ,即ea 1<, 则方程有且仅有两个实根; 如果011ln )1(<-=aa f , 即ea 1>, 则方程没有实根. 如果11ln )1(=-=aa f , 即ea1=, 则方程仅有一个实根.6. 单调函数的导函数是否必为单调函数？研究下面这个例子: f (x )=x +sin x .解 单调函数的导函数不一定为单调函数.例如f (x )=x +sin x 在(-¥,+¥)内是单调增加的, 但其导数不是单调函数. 事实上, f ¢(x )=1+cos x ³0, 这就明f (x )在(-¥, +¥)内是单调增加的. f ¢¢(x )=-sin x 在(-¥, +¥)内不保持确定的符号, 故f ¢(x )在(-¥, +¥)内不是单调的.7. 判定下列曲线的凹凸性: (1) y =4x -x 2; (2) y =sh x ;(3)xy 11+= (x >0);(4) y =x arctan x x ; 解 (1)y ¢=4-2x ,y ¢¢=-2, 因为y ¢¢<0, 所以曲线在(-¥, +¥)内是凸的.(2)y ¢=ch x , y ¢¢=sh x . 令y ¢¢=0, 得x =0. 因为当x <0时, y ¢¢=sh x <0; 当x >0时, y ¢¢=sh x >0, 所以曲线在(-¥, 0]内是凸的, 在[0, +¥)内是凹的. (3)21xy -=¢, 32xy =¢¢.因为当x >0时, y ¢¢>0, 所以曲线在(0, +¥)内是凹的. (4)21arctan xx x y ++=¢,22)1(2x y +=¢¢.因为在(-¥, +¥)内, y ¢¢>0, 所以曲线y =x arctg x 在(-¥, +¥)内是凹的.8. 求下列函数图形的拐点及凹或凸的区间: (1).y =x 3-5x 2+3x +5 ;(2) y =xe -x ; (3) y =(x +1)4+e x ;(4) y =ln(x 2+1); (5) y =e arctan x ;(6) y =x 4(12ln x -7), 解 (1)y ¢=3x 2-10x +3,y ¢¢=6x -10. 令y ¢¢=0, 得35=x .因为当35<x 时, y ¢¢<0; 当35>x 时, y ¢¢>0, 所以曲线在]35 ,(-¥内是是凸的, 在),35[¥+内是凹的, 拐点为)2720,35(.(2)y ¢=e -x-xe -x, y ¢¢=-e -x-e -x+x e -x=e -x(x -2). 令y ¢¢=0, 得x =2. 因为当x <2时, y ¢¢<0; 当x >2时, y ¢¢>0, 所以曲线在(-¥, 2]内是凸的, 在[2, +¥)内是凹的,拐点为(2, 2e -2). (3)y ¢=4(x +1)3+e x , y ¢¢=12(x +1)2+e x . 因为在(-¥, +¥)内, y ¢¢>0, 所以曲线y =(x +1)4+e x的在(-¥, +¥)内是凹的, 无拐点. (4)122+=¢x xy , 22222)1()1)(1(2)1(22)1(2++--=+×-+=¢¢x x x x xx x y . 令y ¢¢=0, 得x 1=-1,x 2=1. 列表得列表得可见曲线在(-¥, -1]和[1, +¥)内是凸的, 在[-1, 1]内是凹的, 拐点为(-1, ln2)和(1, ln2). (5)2arctan 11xe y x+×=¢,)21(12arctan x xey x-+=¢¢. 令y ¢¢=0得, 21=x .因为当21<x 时, y ¢¢>0; 当21>x 时, y ¢¢<0, 所以曲线y =earctg x在]21,(-¥内是凹的, 在) ,21[¥+内是凸的, 拐点是),21(21arctan e .(6) y ¢=4x 3(12ln x -7)+12x 3, y ¢¢=144x 2×ln x . 令y ¢¢=0, 得x =1. 因为当0<x <1时, y ¢¢<0; 当x >1时, y ¢¢>0, 所以曲线在(0, 1]内是凸的, 在[1, +¥)内是凹的, 拐点为(1, -7).9. 利用函数图形的凹凸性, 证明下列不等式:(1) nnny x y x )2()(21+>+ (x >0,y >0, x ¹y , n >1); x (-¥, -1) -1 (-1, 1) 1 (1, +¥) y ¢¢-0 +0 -y Ç ln2 拐点拐点È ln2 拐点拐点Ç(2))(22y x ee e y x yx ¹>++;(3)2ln)(ln ln y x y x y y x x ++>+ (x >0,y >0, x ¹y ). 证明证明 (1)设f (t )=t n, 则f ¢(t )=nt n -1, f ¢¢(t )=n (n -1)t n -2. 因为当t >0时, f ¢¢(t )>0, 所以曲线f (t )=tn 在区间(0, +¥)内是凹的. 由定义, 对任意的x >0, y >0, x ¹y 有 )2()]()([21y x f y f x f +>+,即 nnn y x y x )2()(21+>+.(2)设f (t )=e t, 则f ¢(t )=e t, f ¢¢(t )=e t. 因为f ¢¢(t )>0, 所以曲线f (t )=e t在(-¥, +¥)内是凹的.由定义, 对任意的x , y Î(-¥, +¥),x ¹y 有 )2()]()([21yx f y f x f +>+, 即)(22y x ee e y x yx¹>++.(3)设f (t )=t ln t , 则 f ¢(t )=ln t +1, t t f 1)(=¢¢. 因为当t >0时, f ¢¢(t )>0, 所以函数f (t )=t ln t 的图形在(0, +¥)内是凹的. 由定义, 对任意的x >0,y >0, x ¹y 有 )2()]()([21y x f y f x f +>+, 即 2ln )(ln ln y x y x y y x x ++>+.10. 试证明曲线112+-=x x y 有三个拐点位于同一直线上.证明证明 222)1(12+++-=¢x x x y , 323223)1()]32()][32()[1(2)1(2662++---+=++--=¢¢x x x x x x x x y .令y ¢¢=0, 得x 1=-1, 322-=x , 323+=x . 例表得例表得x (-¥. -1) -1 )32 ,1(-- 32-)32 ,32(+- 32+),32(¥++y ¢-0 +0 - 0 +。