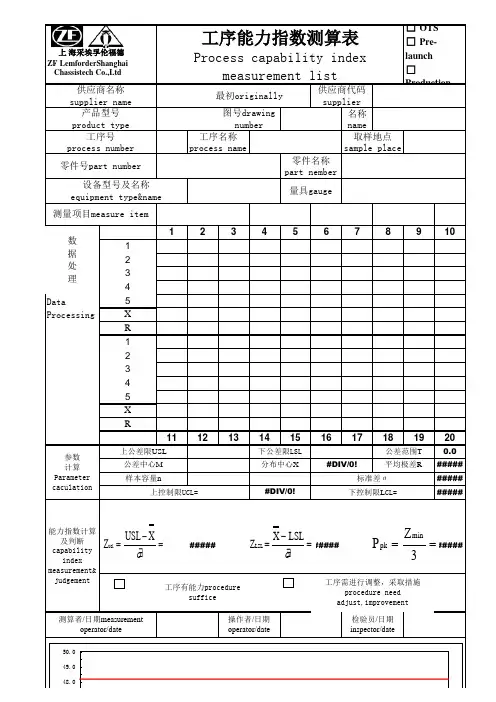
工序能力指数测算表

工序能力指数Cpk计算表1234567891011121314151617181964109154199计算表1#2#Cp 1.09918634CpCpU0.719800509CpUCpL-0.719800509CpLCpk0.719800509CPKT 6.6Tε 1.139ε标准正态累积分0.999512354标准正态累积分CP的P值0.0975292%CP的P值标准正态累积分0.984590485标准正态累积分CPU的P值 1.5409515%CPU的P值标准正态累积分0.015409515标准正态累积分CPL的P值98.4590485%CPL的P值CPK的P值 1.5414103%CPK的P值判断上公差是否FALSE判断上公差是否为空判断下公差是否FALSE判断下公差是否为空结果0.719800509结果P显示结果 1.5414103%P显示结果Cpk Cpk＞1.67过程能力非常充分，为＞1.67过程能＞1.33过程能力充分，当不是＞1.33过程能＞1过程能力尚可，必须用控＞1过程能力＞0.67过程能力不充分，分析＞0.67过程能过程能力不足，一般应停止继过程能力不足1.67≥ 1.67≥1.33≥ 1.33≥1≥1≥0.67＞0.67＞1≥Cpk＞0.67过程能力不充分0.67＞Cp过程频次3#4#0.666666667Cp0Cp0.0721687840.666666667CpU-0.96225045CpU 2.838638824-0.666666667CpL0.962250449CpL-2.694301260.666666667CPK-0.96225045CPK-2.694301260.2T0T0.050ε 1.666666667ε0.9583333330.977249868标准正态累积分0.5标准正态累积分0.5857034624.5500264%CP的P值###########CP的P值82.8593075%0.977249868标准正态累积分0.001946209标准正态累积分12.2750132%CPU的P值99.8053791%CPU的P值0.0000000%0.022750132标准正态累积分0.998053791标准正态累积分3.16213E-1697.7249868%CPL的P值0.1946209%CPL的P值###########4.5500264%CPK的P值###########CPK的P值###########FALSE判断上公差是否为空TRUE判断上公差是否为空FALSEFALSE判断下公差是否为空FALSE判断下公差是否为空TRUE0.666666667结果0.962250449结果 2.8386388244.5500264%P显示结果0.1946209%P显示结果0.0000000%CpL CpU＞1.67过程能力非常充分，为提高产品质量，对过程能力非常充分，为＞1.67过程能力非常充分，＞1.33过程能力充分，当不是关键或主要项目时＞1.33过程能力充分，当不过程能力充分，当不是＞1过程能力尚可，必须用＞1过程能力尚可，必须用控制图或其它方法对程能力尚可，必须用控＞0.67过程能力不充分，分析分散程度大的原因＞0.67过程能力不充分，分过程能力不充分，分析过程能力不足，一般应停止继续加工，找出原因力不足，一般应停止继过程能力不足，一般应停止1.67≥ 1.67≥1.33≥ 1.33≥1≥1≥0.67＞0.67＞CpU＞1.67过程能力非常充分，为提高产品质量Cp过程能力不足，一般1≥CpL＞0.67过程能力不充高产品质量，对关键或主要项目可缩小公差范围；或为提高效率、降低成本而放宽波动幅度，降低设备精度等级；或键或主要项目时，放宽流动幅度；降低对原材料的要求；简化质量检验，采用抽样检验或减少检验频次或其它方法对过程进行控制和监督，以便及时发现异常波动；对产品按正常规定进行检验散程度大的原因，制订措施加以改进，在不影响产品质量的情况下，放宽公差范围，加强质量检验，进行全数检验或加工，找出原因，改进工艺，提高Cp值，否则全检，挑出不合格品提高产品质量，对关键或主要项目可缩小公差范围；或为提高效率、降低成本而放宽波动幅度，降低设备精度等级降低设备精度等级；或将精度要求特别高的零件调至该工序进行加工等检验，进行全数检验或增加检验频次度，降低设备精度等级；或将精度要求特别高的零件调至该工序进行加工等。

工序能力指数的判断与计算工序能力指数（CPK ）一）工序能力与工序能力指数工序能力，是指工序在一定时间，处于操纵状态（稳固状态）下的实际加工能力，它是工序固有的能力，或者者说它是工序保持质量的能力。

这里所指的工序，是指操作作者、机器、原材料、工艺方法与生产环境等五个基本质量因素综合作用的过程，也就是产品质量的生产过程，产品质量也就是工序中的各个质量因素的起作用的综合表现。

关于任何生产过程，产品质量总是分散地存在着，若工序能力越高，则产品质量特性值的分散就会越小；若工序能力低，则产品质量特性值的分散就会越大，那么，应当用一个什么样的量来描述生产过程所造成的总分散呢？通常，都用6 （即时 ）来表示工序能力：工序能力为=6 。

若用符号P 来表示工序能力，则P=6 （其中的 是处于稳固状态下的工序之标准偏差）。

工序能力与通常所说的生产能力是两个不一致的概念。

前者是指质量上的能力，后者是指数量上的能力。

工序能力是表示生产过程客观存在着分散的一个参数。

但是，这个参数能否满足产品的技术要求（公差、规格等质量标准）的程度，这个参数就叫做工序能力指数，它是技术要求与工序能力的比值，即：σσμ3±σ工序能力技术要求工序能力指数=σσ当分布中心与公差中心重合时，工序能力指数记为Cp，当分布中心与公差中心偏离时，工序能力指数记为CPK，运用工序能力指数，能够帮助我们掌握生产过程的质量水平。

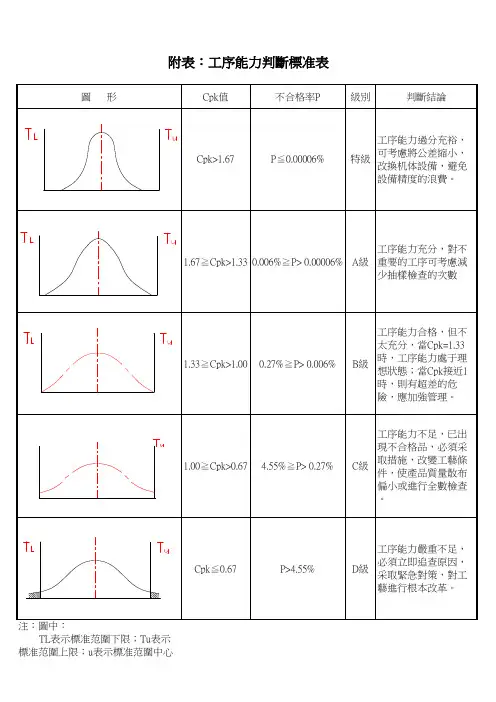
二）工序能力指数的推断工序的质量水平按Cp值能够划分为5个等级。

按其等级的高低，在管理上可作下列推断与处理，该表中的分级推断与处理关于CPK也同样运用。

工序能力指数的分级推断与处置参考表三）工序能力指数的计算1、在介绍工序能力指数计算往常，先介绍一下平均值与标准偏差的计算：平均值的数学表达式：标准偏差的数学表达式：在实际过程中，由于所取的数据通常较多（100个左右），这样用数学表达式来计算标准偏差十分烦恼，因此，在生产现场常得用作直方图过程中的频数表，使用两种简化的办法来求解平均值与标准偏差，这里不一一作介绍。

工序能力指数（CPK ）一）工序能力和工序能力指数工序能力，是指工序在一定时间，处于控制状态（稳定状态）下的实际加工能力，它是工序固有的能力，大概说它是工序保持质量的能力。

这里所指的工序，是指操纵作者、呆板、原质料、工艺要领和生产情况等五个根本质量因素综互助用的历程，也就是产物质量的生产历程，产物质量也就是工序中的各个质量因素的起作用的综合体现。

对付任何生产历程，产物质量总是疏散地存在着，若工序能力越高，则产物质量特性值的疏散就会越小；若工序能力低，则产物质量特性值的疏散就会越大，那么，应当用一个什么样的量来描述生产历程所造成的总疏散呢？通常，都用6 （即时 ）来体现工序能力：工序能力为=6 。

若用标记P 来体现工序能力，则P=6 （其中的 是处于稳定状态下的工序之尺度偏差）。

工序能力与一般所说的生产能力是两个差别的观点。

前者是指质量上的能力，后者是指数量上的能力。

工序能力是体现生产历程客观存在着疏散的一个参数。

但是，这个参数能否满足产物的技能要求（公差、规格等质量尺度）的水平，这个参数就叫做工序能力指数，它是技能要求和工序能力的比值，即：σσμ3±σ工序能力技术要求工序能力指数=σσ当漫衍中心与公差中心重适时，工序能力指数记为Cp ，当漫衍中心与公差中心偏离时，工序能力指数记为CPK ，运用工序能力指数，可以资助我们掌握生产历程的质量水平。

二）工序能力指数的判断工序的质量水平按Cp 值可以分别为5个品级。

按其品级的崎岖，在治理上可作以下判断和处理惩罚，该表中的分级判断和处理惩罚对付CPK 也同样运用。

工序能力指数的分级判断和处理参考表三）工序能力指数的盘算1、在介绍工序能力指数盘算以前，先介绍一下平均值和尺度偏差的盘算：平均值的数学表达式：NN Xn X X X X∑=---+++=321μ尺度偏差的数学表达式：在实际历程中，因为所取的数据一般较多（100个左右），这样用数学表达式来盘算尺度偏差十分麻烦，所以，在生产现场常得用作直方图历程中的频数表，接纳两种简化的步伐来求解平均值和尺度偏差，这里不一一作介绍。

工序能力指数的计算方法：
(1)双侧偏差：（Tu、Tl）a，公差中心与分布中心重合：Cp b 不重合Cpk
(2)单侧偏差：（Tu或Tl）a，只有上侧偏差:CpTu=（Tu-x）/3σ
Cpk的评级标准：（可据此标准对计算出之制程能力指数做相应对策）
A++级Cpk≥2.0 特优可考虑成本的降低
A+ 级 2.0 >Cpk ≥ 1.67 优应当保持之
A 级 1.67 > Cpk ≥ 1.33 良能力良好，状态稳定，但应尽力提升为A+级
B 级 1.33 >Cpk ≥ 1.0 一般状态一般，制程因素稍有变异即有产生不良的危险，应利用各种资源及方法将其提升为A级
C 级 1.0 >Cpk ≥ 0.67 差制程不良较多，必须提升其能力
D 级 0.67 >Cpk>0 不可接受其能力太差，应考虑重新整改设计制程。

一般来说，我们采取的判定基准值为Cpk ≥ 1.33。

工序能力指数CPK的计算和分析CPK的计算公式如下：CPK = min（USL - μ，μ - LSL）/（3 * σ）其中，USL为规格上限，LSL为规格下限，μ为平均值，σ为标准差。

CPK的值越大，表示工序的稳定性和可控性越强。

一般来说，CPK值大于1.33被认为是良好的，大于1.67则被认为是极好的。

而CPK值小于1则表示工序不稳定或者不可控。

CPK的分析可以从以下几个方面进行：1.变异性分析：通过计算标准差和绘制控制图来评估工序的变异性。

如果标准差较小，并且控制图上的数据点在控制界限内，则说明工序具有较小的变异性，可以认为是稳定的。

反之，则说明工序存在较大的变异性，需要进一步改进。

2.规格限值分析：通过比较规格限值和平均值，以及计算CPK值，来评估工序是否能够满足产品的规格要求。

如果CPK值大于1，则说明工序具有足够的能力满足规格要求。

如果CPK值小于1，则需要进行进一步的改进，以提高工序的能力。

3.误差源分析：通过分析工序中可能存在的误差源，找出和改进引起工序不稳定的原因。

误差源可能包括人为因素、设备问题、材料质量等。

通过改进和优化这些误差源，可以提高工序的稳定性和可控性。

4.过程能力改进：通过改进工序中的控制措施和方法，来提高工序的能力。

例如，可以采用六西格玛等质量管理工具，优化工序的流程和参数设定，以减少变异性和提高工序的能力。

总之，CPK是评估工序稳定性和可控性的重要指标，可以通过计算和分析CPK值来评估工序的能力，并通过改进控制措施和优化过程来提高工序的能力。

工序能力指数（CPK ）一）工序能力和工序能力指数工序能力，是指工序在一定时间，处于控制状态（稳定状态）下的实际加工能力，它是工序固有的能力，或者说它是工序保持质量的能力。

这里所指的工序，是指操作作者、机器、原材料、工艺方法和生产环境等五个基本质量因素综合作用的过程，也就是产品质量的生产过程，产品质量也就是工序中的各个质量因素的起作用的综合表现。

对于任何生产过程，产品质量总是分散地存在着，若工序能力越高，则产品质量特性值的分散就会越小；若工序能力低，则产品质量特性值的分散就会越大，那么，应当用一个什么样的量来描述生产过程所造成的总分散呢？通常，都用6 （即时 ）来表示工序能力：工序能力为=6 。

若用符号P 来表示工序能力，则P=6 （其中的 是处于稳定状态下的工序之标准偏差）。

工序能力与一般所说的生产能力是两个不同的概念。

前者是指质量上的能力，后者是指数量上的能力。

工序能力是表示生产过程客观存在着分散的一个参数。

但是，这个参数能否满足产品的技术要求（公差、规格等质量标准）的程度，这个参数就叫做工序能力指数，它是技术要求和工序能力的比值，即：σσμ3±σ工序能力技术要求工序能力指数=σσ当分布中心与公差中心重合时，工序能力指数记为Cp，当分布中心与公差中心偏离时，工序能力指数记为CPK，运用工序能力指数，可以帮助我们掌握生产过程的质量水平。

二）工序能力指数的判断工序的质量水平按Cp值可以划分为5个等级。

按其等级的高低，在管理上可作以下判断和处理，该表中的分级判断和处理对于CPK也同样运用。

工序能力指数的分级判断和处置参考表三）工序能力指数的计算1、在介绍工序能力指数计算以前，先介绍一下平均值和标准偏差的计算：平均值的数学表达式：标准偏差的数学表达式：在实际过程中，因为所取的数据一般较多（100个左右），这样用数学表达式来计算标准偏差十分麻烦，所以，在生产现场常得用作直方图过程中的频数表，采用两种简化的办法来求解平均值和标准偏差，这里不一一作介绍。

工序能力指数CPK的计算和分析工序能力指数CPK的计算和分析工序能力工序能力是指工序在一定时间里，处于控制状态（稳定状态）下的实际加工能力。

它是工序固有的能力，或者说它是工序保证质量的能力。

这里指的工序，是指操作者、机器、原材料、工艺方法和生产环境等五个基本的质量因素综合作用的过程，也就是产品质量的生产过程。

产品质量就是工序中的各个质量因素所起作用的综合表现。

对于任何生产过程，产品质量总是分散地存在着。

若工序能力越高，则产品质量特性值的分散就会越小；若工序能力越低，则产品质量特性值的分散就会越大。

应当用一个什么样的量来描述生产过程所造成的总分散呢？通常，都用6σ（即μ±3σ）来表示工序能力：工序能力＝6σ若用符号P来表示工序能力，则 P ＝6σ式中：σ是处于稳定状态下的工序的标准偏差。

工序能力与一般所讲的生产能力是两个不同概念。

前者是指质量上的能力，后者是指数量上的能力。

工序能力指数工序能力是表示生产过程客观存在着分散的一个参数。

但是这个参数是否满足产品的技术要求，仅从它本身还难以看出。

因此需要另一个参数来反映工序能力满足产品技术要求（公差、规格等质量标准）的程度。

这个参数就叫做工序能力指数。

它是技术要求和工序能力的比值，即工序能力指数＝技术要求/ 工序能力当分布中心与公差中心重合时，工序能力指数记为C P。

当分布中心与公差中心有偏离时，工序能力指数记为C PK.运用工序能力指数，可以帮助我们掌握生产过程的质量水平。

工序能力指数的分级判断工序的质量水平按C P值可划分为五个等级。

按其等级的高低，在管理上可以作出相应的判断和处置见下表下表中的分级、判断和处置对C PK也同样适用。

表2-4-11 工序能力指数的分级判断和处置参考表（C P、C PK）C P 值级别判断双侧公差范围（T）处置CP >1.67特级能力过高T > 10σ1.可将公差缩小到约±4σ的范围。

2.允许较大的外来波动，以提高效率。

力工序能工序能力是指工序在一定时间里，处于控制状态（稳定状态）下的实际加工能力。

它是工序固有的能力，或者说它是工序保证质量的能力。

这里指的工序，是指操作者、机器、原材料、工艺方法和生产环境等五个基本的质量因素综合作用的过程，也就是产品质量的生产过程。

产品质量就是工序中的各个质量因素所起作用的综合表现。

对于任何生产过程，产品质量总是分散地存在着。

若工序能力越高，则产品质量特性值的分散就会越小；若工序能力越低，则产品质量特性值的分散就会越大。

应当用一个什么样的量来描述生产过程所造成的总分散呢？σ）来表示工序能力：σ（即μ±3通常，都用6 σ＝ 6工序能力6σ来表示工序能力，则若用符号P P ＝式中：σ是处于稳定状态下的工序的标准偏差。

工序能力与一般所讲的生产能力是两个不同概念。

前者是指质量上的能力，后者是指数量上的能力。

工序能力指数但是这个参工序能力是表示生产过程客观存在着分散的一个参数。

数是否满足产品的技术要求，仅从它本身还难以看出。

因此需要另一个参数来反映工序能力满足产品技术要求（公差、规格等质量标准）的程度。

这个参数就叫做工序能力指数。

它是技术要求和工序能力的比值，即工序能力指数＝技术要求 / 工序能力当分布中心与公差中心重合时，工序能力指数记为C。

P当分布中心与公差中心有偏离时，工序能力指数记为C.PK运用工序能力指数，可以帮助我们掌握生产过程的质量水平。

工序能力指数的分级判断工序的质量水平按C值可划分为五个等级。

按其等级的高低，在管P理上可以作出相应的判断和处置见下表下表中的分级、判断和处置对C也同样适用。

PK表2-4-11 工序能力指数的分级判断和处置参考表（C、C ）PKP．Tμ为分布中心M为公差中心TL μ TU(M)图2-4-18分布中心与公差中心重合时工序能力指数的计算从分布中心的位置看，这是一种理想的情况（见图2-4-18）。

这种情况下，工序能力指数的计算可用下式进行。

工序能力指数（CPK ）一）工序能力和工序能力指数工序能力，是指工序在一定时间，处于控制状态（稳定状态）下的实际加工能力，它是工序固有的能力，或者说它是工序保持质量的能力。

这里所指的工序，是指操作作者、机器、原材料、工艺方法和生产环境等五个基本质量因素综合作用的过程，也就是产品质量的生产过程，产品质量也就是工序中的各个质量因素的起作用的综合表现。

对于任何生产过程，产品质量总是分散地存在着，若工序能力越高，则产品质量特性值的分散就会越小；若工序能力低，则产品质量特性值的分散就会越大，那么，应当用一个什么样的量来描述生产过程所造成的总分散呢？通常，都用6 （即时 ）来表示工序能力：工序能力为=6 。

若用符号P 来表示工序能力，则P=6 （其中的 是处于稳定状态下的工序之标准偏差）。

工序能力与一般所说的生产能力是两个不同的概念。

前者是指质量上的能力，后者是指数量上的能力。

工序能力是表示生产过程客观存在着分散的一个参数。

但是，这个参数能否满足产品的技术要求（公差、规格等质量标准）的程度，这个参数就叫做工序能力指数，它是技术要求和工序能力的比值，即：σσμ3±σ工序能力技术要求工序能力指数=σσ当分布中心与公差中心重合时，工序能力指数记为Cp，当分布中心与公差中心偏离时，工序能力指数记为CPK，运用工序能力指数，可以帮助我们掌握生产过程的质量水平。

二）工序能力指数的判断工序的质量水平按Cp值可以划分为5个等级。

按其等级的高低，在管理上可作以下判断和处理，该表中的分级判断和处理对于CPK也同样运用。

工序能力指数的分级判断和处置参考表三）工序能力指数的计算1、在介绍工序能力指数计算以前，先介绍一下平均值和标准偏差的计算：平均值的数学表达式：标准偏差的数学表达式：在实际过程中，因为所取的数据一般较多（100个左右），这样用数学表达式来计算标准偏差十分麻烦，所以，在生产现场常得用作直方图过程中的频数表，采用两种简化的办法来求解平均值和标准偏差，这里不一一作介绍。