初始过程能力指数Ppk测算表

測量單位 mm
製表 Người lập
審核 Xét duyệt
核准 Phêduyệt
管理值 規格幅度(T)： 1.000
平均值(X)： 9.663 標準差(σ)： 0.067 製程能力(Pp)： 2.495 製程能力(Ppk)： 1.681
σ能力： 7.5 σ水準： 5.0
3.308
算術公式 規格的上限 - 下限值
Pp ＜ 1.33
能力不足
※ 分析意見 ※
製程能力判定
○ (能力充分)
測定值的 平均
區分
○
σ = Σ(x-xi)² n-1
△
Pp = T/(6×σ)
×
Ppk=MIN[{(規格上限-M)/(3 ×σ)} ,{(M-規格上限)/(3 ×σ)}]
σ能力= Pp ×3
σ水準= Ppk ×3
判定基準及分析
重要度
工程特性
1.67 ≤Pp
能力充分
1.67 ＞Pp ≥1.33 需 改 善
工件編號
初始製程能力(Ppk)分析表
文件版次
A0
工件名稱
分析類別
PPAP
客戶名稱
抽樣數量
30PCS
生產線別 Chuyền sản xuất 重要檢查項目/數值： 尺寸高度 / 9.5 ±0.5
測定日期
2016/1/8
工 程
PP： 2.495
能
力
指 數
PPK： 1.681
1～10 11～20 21～30 31～40 41～50 51～60 61～70 71～80 81～90 91～100規格數值9.719.749.77
9.73
9.66
9.58

用于判定初始过程能力的指数主要有Cpk指数和Cmk指数。

1. Cpk指数：它考虑了过程的中心位置，用来评估过程的能力是否满足规范要求并且中心位置是否合理。

Cpk指数的计算公式如下：Cpk = (USL - LSL) / (6 * σ)，其中USL为规范上限，LSL为规范下限，σ为过程的标准差。

2. Cmk指数：它是德国汽车行业常采用的参数，是"Machine Capability Index" 的缩写，称为临界机器能力指数，它仅考虑设备本身的影响，同时考虑分布的平均值与规范中心值的偏移。

希望以上信息对你有帮助，建议咨询专业人士获取更准确的信息。

製程特性依不同的工程規格其定義如下：。

等級處理原則無規格界限時Cp(Pp)＝＊＊＊Cpk(Ppk)＝＊＊＊Ca ＝＊＊＊單邊上限(USL) Cp(Pp)＝CPUCpk(Ppk)＝CPUCa ＝＊＊＊單邊下限(LSL) Cp(Pp)＝CPLCpk(Ppk)＝CPLCa ＝＊＊＊雙邊規格(USL, LSL) Cp(Pp)＝(USL－LSL)／6σCpk(Ppk)＝MIN(CPU,CPL)Ca ＝|平均值－規格中心|／(公差／2)谈到过程能力，首先得解释变异（或者叫波动），正是因为有了变异的存在，才出现了能力大小。

产生变异的原因可以归结为两种，一种是普通原因，一种是特殊的原因。

所谓的普通原因就是平时一直客观存在，对过程有一定的影响但不明显，而特殊因素则是偶然出现，对过程影响很大。

举例说明：在一个有空调的房间进行培训时，虽然空调可能是设定在25度，但由于房间内外温度存在差异，所以每时每刻都会有能量在和房间外进行交换，所以如果用足够精确的温度计测量房间的温度就会发现房间里的温度其实并不是恒定在25.000度，而是24.99,24.98,25.00,25.01…..在微小的在一定范围内进行变化，这时我们就说受到的是普通因素的影响，而如果有人推门进来，那么在这瞬间，房间内的温度会出现较大变化，此时我们说受到了普通因素和特殊因素两种影响。

过程只受普通因素影响的时候在控制图上表现为过程是受控的，如果有特殊原因的影响在控制图上会有异常点的出现。

所以我们如果用Cp和Cpk来衡量过程能力，前提是要过程稳定且数据是正态分布，而且数据应该在25组以上（建议最少不要低于20组，数据组越少采信结果的风险越大），也就是说计算Cp,Cpk只考虑过程受普通因素的影响。

计算公式为：Cp=(usl-lsl)/6σ;1、Cpk=(1-k)Cp;k=|u-M|/(usl-lsl)/2;2、Cpk=min{(usl-u)/3σ ,(u-lsl)/3σ };注释：usl为上规格线，lsl 为下规格线，u为实际测得的平均值，M为上下规格的中心点，K值表示的意思是实际平均值偏离中心值的程度，此时的即为只考虑普通因素产生的变异，通常根据控制图的不同采用Rbar/d2,或者Sbar/C4,在minitab里有三种不同的估算方法。

1 2 3 4 5 TOTAL AVERAGE(X) CLX UCLX LCLX MAX-MIN(R) CLR UCLR LCLR
制表/日期:
X-CHART ● R-CHART 检 查 记 录
2.130
组容
2.100
A2
1.88
D3
*
D4
3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
2.170 2.160 2.174 2.170 2.160
2.1668 2.1509 2.1864 2.1153 0.0140 0.0127 0.0268 0.0000
2.150 2.150 2.150 2.140 2.150
2.1480 2.1509 2.1864 2.1153 0.0109 0.0127 0.0268 0.0000
初始过程能力分析报告
工厂车间 零件名称 ● X=AVE（X）=
2.190
CZ-0095
2.200 2.100 LCLX=X-A2R= 组容/频率 图 2.12
AVERAGE(X)
机械加工
工序名称 机器编号
数控铣一面 023-04
质量特性 规 格 值 2.19
重要 2.20
公差上限 公差下限
125/5
2.150 2.150 2.140 2.150 2.160
2.1500 2.1509 2.1864 2.1153 0.0200 0.0127 0.0268 0.0000
2.150 2.160 2.150 2.160 2.150
2.1540 2.1509 2.1864 2.1153 0.0100 0.0127 0.0268 0.0000

1 1.000 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
0.995
0.990
R ¼ Í
0.006 0.005 0.004
0.003
0.002 0.001 0.000 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
序 号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
时 间
测 X1
99.40% 99.40% 99.60% 99.70% 99.56% 99.60% 99.46% 99.40% 99.50% 99.45% 99.40% 99.62% 99.36% 99.60% 99.50% 99.41% 99.47% 99.48% 99.50% 99.42% 99.45% 99.32% 99.65% 99.42% 99.52%
审批者(签名)：
第 2 页 共2页
计 X5
99.40% 99.56% 99.50% 99.58% 99.50% 99.50% 99.58% 99.53% 99.30% 99.50% 99.45% 99.68% 99.58% 99.50% 99.63% 99.58% 99.67% 99.46% 99.40% 99.56% 99.35% 99.58% 99.40% 99.46% 99.58%
算 R
0.002 0.002 0.003 0.004 0.002 0.001 0.002 0.002 0.002 0.002 0.002 0.003 0.002 0.002 0.002 0.003 0.003 0.003 0.004 0.002 0.003 0.003 0.003 0.002 0.003 0.060

CPCPKPPPPKCMK的计算公式过程能力指数公式在质量管理中，过程能力指数是用于衡量一个过程的稳定性和性能的指标。

它们可以帮助我们评估一个生产过程是否能够达到预期的质量水平。

以下是CP、CPK、PP、PPK和CMK的计算公式及其过程能力指数的定义：1.CP(过程能力指数)CP是最常用的过程能力指数，它用于评估一个过程的稳定性和可控性。

CP表示过程能力与产品的规格要求之间的比例关系。

CP的计算公式为：CP=(USL-LSL)/(6*标准差)其中，USL是上限规格限制，LSL是下限规格限制。

CP的值越接近1，表示该过程越能够满足规格要求。

如果CP小于1，则表示过程能力不足以满足规格要求。

2.CPK(过程能力指数)CPK是一种综合性的过程能力指数，它不仅考虑了过程的稳定性，还考虑了过程的中心位置。

CPK可以帮助我们评估过程是否能够在正常分布曲线的两侧均能满足规格要求。

CPK的计算公式为：CPK = min((USL - 平均值) / (3 * 标准差), (平均值 - LSL) / (3 * 标准差))CPK的值越接近1，表示该过程越能够满足规格要求。

如果CPK小于1，则表示过程能力不足以满足规格要求。

3.PP(过程性能指数)PP用于评估长期过程的能力，即过程在不同时间段内的表现。

PP基于过程能力指数CP的基础上，考虑了过程的长期变化。

PP的计算公式为：PP=(USL-LSL)/(6*标准差)PP的值越接近1，表示过程在不同时间段内的表现越能够满足规格要求。

如果PP小于1，则表示长期过程能力不足以满足规格要求。

4.PPK(过程性能指数)PPK是一种综合性的过程性能指数，它不仅考虑了过程的稳定性，还考虑了过程的中心位置。

PPK可以帮助我们评估长期过程是否能够在正常分布曲线的两侧均能满足规格要求。

PPK的计算公式同CPK的计算公式：PPK = min((USL - 平均值) / (3 * 标准差), (平均值 - LSL) / (3 * 标准差))PPK的值越接近1，表示长期过程在不同时间段内的表现越能够满足规格要求。

过程能力计算及评价方法1.过程能力等级说明1.1 Cp评价等级——《质量专业理论与实务》（中级）1.2 无偏时Cp与合格（不合格）率的对应关系由上表可知，在无偏时Cp与合格（不合格）率的对应关系是非线性的一一对应的关系，过程能力指数越大，合格率越高（反之亦然）。

——《六西格玛管理质疑》1.3 Cpk1.4 Pp 、Ppk 评价等级A ）Pp 、Ppk > 1.67 该过程目前能满足和符合顾客要求。

顾客批准后即可开始生产，并按照控制计划进行。

B ） 1.33 ≤ Ppk ≤ 1.67 该过程目前可能被顾客接受，但是可能会被要求进行一些改进。

与顾客取得联系，并评审研究结果，如果在批量生产开始之前仍没有改进，将要求对控制计划进行更改。

C ） Ppk < 1.33 该过程目前不能满足和符合顾客要求。

与顾客取得联系，并对研究结果进行评审，对需改进的过程必须有书面的纠正措施计划，增加检验与试验频率直到Cpk>1.33为止，修改后的控制计划应经顾客批准。

——《PPAP 手册》1.5 过程中的过程能力要求A ）过程稳定且数据呈常（正）态分配时，过程能力指数须达到Cpk ≧1.33。

B ）长期不稳定的过程，但是SPC 抽检样本的质量符合规格且呈可预测的型态时，初期过程能力指数须达到Ppk ≧1.67。

2. 计算公式2.1 过程能力指数计算公式过程能力——仅使用统计稳定的过程，是过程固有变差的6σ范围，σ通常用“R /d2”或者“s/c4”来估计。

过程性能——过程总变差的6σ范围，σ通常用样本的标准差s 来估计。

——《SPC 手册》σε62)1(-=-=T Cp K Cpk2.2 短期过程能力指数与过程性能指数公式比较——《质量专业理论与实务》（中级）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
AVG.
研究评定:由以上计算结果可知PPK= ##### ＞1.67,初始能力指数足够.若批准,开始生产并按照已批准的控制计划进行.
说明：试生产时前期质量部连续取样125件对产品特性进行测量并记录结果，提交前期质量科长审批签字后存档，下发至相关责任单位，并将结果反馈至项目经理。
2
1.13 1.88 1.69 1.02 2.06 0.73 2.33 0.58 2.53 0.48
Ppk1= (USL-X)/3δ s= ####
2.7 0.42 0.08 1.92 1 2.85 0.37 0.14 1.86 2 2.97 0.34 0.18 1.82 3 3.08 0.31 0.22 1.78 4 5。
初始过程能力研究报告（PPK）
表单编号： 工 厂 Rev：A 部 日 门 期 X-R控 制 图 数 据 表 格 工 特 序 性 计算控制限日期 样本容量/频率 工程规范 零件编号 保存期限 3年
机器编号 日期/时间 1 读 2 3 数 4 5 和
0.000 #### #### #### 0.000 #### #### 0.000 #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### ####
X=和/读数数量 ##### #### #### #### ##### #### #### ##### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### R=最高—最低 0.000 #### #### #### 0.000 #### #### 0.000 #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### #### S=STDEV(C6:V10)=δ s= #### 参 数 d2 X= ##### R= #### 子 2 3 4 UCLX=X+A2R= USL= ##### 4.400 UCLR=D4R= 0 组 5 6 容 LCLX=X A2R= ##### 4.000 LCLR=D3R= 0 量 7 8 9 10 A2 表 D3 * * * * * D4 3.27 2.57 2.28 2.11 2.00 采取措施的说明： 对特殊原因采取的措施的说明： * 任何超出控制限的点。 * 连续7点全在中心线之上或之下。 * 连续7点上升或下降。 * 任何其它明显非随机的图形。

Cgk, Cmk, Ppk, Cpk能力指数介绍CgK, Cmk, Ppk, Cpk应用技术Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍CpkCgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍CgK, Cmk, Ppk, Cpk评级标准涉及Cp评价等级要求值状态处理方案A级 1.33≤Cp 稳定可考量缩小规格B级 1.0＜Cp ≤1.33 一般必须加以注意，维持C 级0.83＜Cp ≤1.0 危险检讨规格及作业标准D级Cp≤0.83 极差停机，重新调整后生产Cp=(Usl-Lsl)/6s; 单边Cp=Cpk=Cpu=Cpl=规格容许差/3s注：Cp 值越大，分布数据接近，但也有可能偏于中心值的分布规格U-L 中心值M密度高-----低u 密集命中密度高分散命中密度低密集命中密度高，但偏离大规格宽松，须缩小提高设备精度或放宽规格修改中心值，缩小规格范围Cgk, Cmk, Ppk, Cpk能力指数介绍Cgk, Cmk, Ppk, Cpk能力指数介绍结束语：1. 通过以上各种能力指数的分析，可以针对工作需要选用或并用多种工具，了解4M等因素或制程能力，确保生产品质是否在掌握范围？2. 任何一种统计工具都要灵活运用，不可极端采纳。

3. 目前管制线一般采用+3s～-3s，直通率为99.73%作为基准线，来做SPC管制线以上报告，仅供参考。

初始过程能力研究报告-PPK1. 引言1.1 研究背景与意义随着全球经济一体化的推进，市场竞争日益激烈，企业对产品和过程的质量要求也在不断提高。

初始过程能力（Process Performance Index, PPK）作为衡量生产过程稳定性的重要指标，是企业在生产初期就确保产品质量，降低成本，提高竞争力的关键。

在我国，许多企业在初始过程能力方面仍存在不足，导致生产效率低下，资源浪费严重。

因此，深入研究初始过程能力PPK，对提高我国制造业的整体水平具有重要的现实意义。

1.2 研究目的与内容本研究旨在探讨初始过程能力PPK的评估与改进方法，以期为企业提供有效的过程优化策略。

研究内容主要包括：PPK的定义与计算方法、应用领域、评估指标与标准、评估流程与步骤以及改进策略等。

通过案例分析，验证所提出方法的有效性，为企业提供实际操作指导。

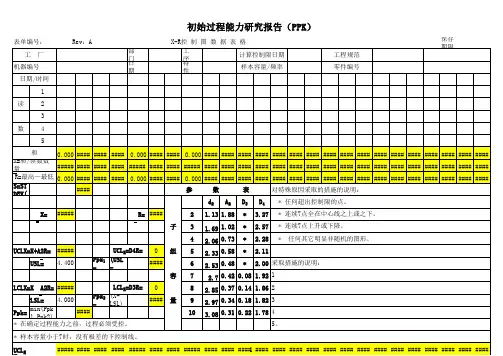
2. 初始过程能力PPK概述2.1 PPK的定义与计算方法PPK（Process Performance Index）即过程性能指数，是衡量初始过程能力的一个重要参数。

它是通过对过程数据的统计分析得出的，反映了过程输出满足规格要求的程度。

PPK的计算基于过程均值和标准差，其公式如下：[ PPK = ]其中，USL（Upper Specification Limit）为规格上限，LSL（Lower Specification Limit）为规格下限，σ（sigma）为过程标准差。

PPK的取值范围为0到1，PPK值越大，表示过程能力越强，过程输出满足规格要求的概率越高。

通常，PPK值在0.67以上被认为是过程能力良好。

2.2 PPK的应用领域PPK在制造业中有着广泛的应用，主要表现在以下几个方面：1.新产品开发：在新产品开发阶段，通过计算PPK值，可以评估过程能力是否满足设计要求，从而为产品的设计和生产提供依据。

2.过程改进：通过对PPK值的监测，可以发现过程中的问题，指导企业进行过程改进，提高产品质量。

27
28
29
30
28.9 27.9 27.6 28.7
镀镍层厚度曲线表
30 29 28 27 26
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
镀镍层厚度曲线表
分 析 评 定：该设备能力满足要求。
24
25
26
28.9 29.2 28.8 28.1
X=28.3967 n
δ= ∑(Xi—X）2/（n-1）=0.6553 i=1
CPL=X-LSL / 3δ=1.728
QR—0703—38
设备名称： 半镍槽 / 光亮镍槽
7
8
9
10
28.4 28.1 29.5 28.2
17
18
19
20
27.4 28.1 27.6 28.5
2 27.6
12 27.9
22 29
工序编号 / 名称 ：60 /半光亮镍、62 / 光亮镍
3
4
5
6
27.9 28.2 29.6 27.9
13
14
15
16
28
27.8 29.1 28.5
23
24
25
26
28.9 29.2 28.8 28.1
X=28.3967 n
δ= ∑(Xi—X）2/（n-1）=0.6553 i=1
镀铜层厚度曲线表
分 析 评 定：该设备能力满足要求。
需采取措施：
检查员：
工艺员：
操作者：
项目负责人：
长春高新汽车饰件材料 制造有限公司（CGA）

一、 双侧公差情况的过程能力指数1﹑对于侧公差能情况，过程能力指数CP 的定义如下； σσ66L U T T T CP −== ① T 为技术公差的幅度，u t ﹑L t 分别为上﹑下公差限，σ为质量特性值分布的总体标准差。

当σ未知时，可用σ=R （bar ）/d2或σ=S （bar ）/C4估计，其中R 为样本的极差，R （bar ）为平均数，S 为样本的标准差，S （bar ）为平均数；D2、C4为修正系数，可根据样本组的个数查表获得；注意；估计值必须在稳定的状态下进行，在GB/T4091-2001《常规控制图》中有明确的规定；当CP=2、σ=0·5时，P=2ppm=2×910=。

事实上，从CP=1，σ=1时，可以得出CP=1=T/6σ，即T=6，于是σ-1/CP 。

故对于CP=2，σ=1/2=0·5，也就是说能力指数与不合格率是一一对应的。

二、单侧公差情况的能力指数1、 若只有上限要求时，而对下限没有要求时，则过程能力指数计算如下；σµ3−=U PU T C （μ< T U ） C PU 为上单侧过程能力指数，当μ≥TU 时，记作C PU =0上限要求2、 若只有下限要求时，而对上限没有要求时，则过程能力指数计算如下；σµ3lpl t c −= （μ>T L ）C PL 为下单侧过程能力指数，当μ≤TL 时，记作C PL =0下限要求上面二例中的μ与σ未知时，可用样本估计，例如用X （bar ）估计μ，用S 估计σ，三、有偏移情况的过程能力指数当产品质量特性分布的均值μ与公差中心Μ不重合，即有偏移时，不合格率必然回增大，CP 值降低，当过程能力指数不能反映有偏移的实际情况，需要加以修正，记修正后的过程能力指数为CPK ，则计算公式为；),min(PL PU C C CPK =记作分布中心μ对于公差中心M 的偏移为ε=|M-μ|，定义μ与M 的相对偏移（偏移度）K 为； TT k εε22/== （0≤K <1） 则过程能力指数修正为； ∧−≈−=−=σσ6)1(6)1()1(T K T K C K C P PK 这样，当μ=M （即分布中心与公差中心重合无偏移）时，K=0，CPK=CP ，注意CPK 也必须是在稳定状态下求得；美国的三大汽车公司（福特Ford 、通用GE 、克莱斯特Crysler ）联合制定了QS —9000标准，对于统计方法的应用提出更高的要求，QS —9000标准的认证是以ISO9000标准的认证为前提的，在QS 中提出PP 、PPK 的新概念，称之为过程性能指数（Process Perfomance Index ），又称为长期过程能力指数。

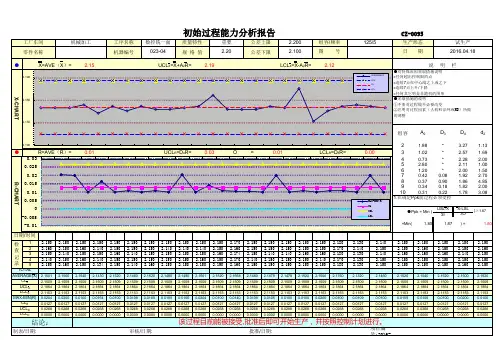
设备名称元件型号钢网厚度设备编号抽样形态规格中心值机种名称抽样数量规格上限单位抽样日期规格下限序号12345678910X bar 1121.33111.61121.06110.83119.84111.06120.35116.12118.77115.79116.682109.67122.38112.67121.63112.24120.35112.83118.32114.17120.46116.473120.72114.83121.31112.60120.88111.97120.74116.27122.69113.89117.594110.35121.39110.06117.20109.68120.56113.73121.09112.63121.92115.865120.97112.43118.23110.24122.80111.85120.45113.72120.52115.67116.696113.59120.31110.54118.75113.98122.07109.97121.39113.62120.65116.497122.25107.52121.20111.94121.39111.12119.31113.22120.59112.84116.148111.41120.30109.73123.68110.96119.82113.08117.02116.23119.46116.179122.97110.08120.20112.07118.75110.25121.92114.14120.85113.85116.5110111.61121.99108.90120.51112.60119.62113.85119.37113.02122.77116.4211121.89105.53122.60111.16123.50113.63117.92115.68120.66110.05116.2612112.71119.11111.72120.29114.00124.28113.34117.63113.04119.56116.5713122.66109.58122.38111.49121.63111.28118.34113.88119.01113.46116.37产品设计变更生产审核：品保审核：工程审核：核准：实际抽样值抽样时机4.593.383.38PPK：PPK=（USL-`X ）/3σ或（`X -LSL）/3σ=((USL-LSL)/2+(USL+LSL)/2-`X ）/3σ或((USL-LSL)/2-(USL+LSL)/2+`X )/3σ两者求最小值制程更改公差缩小分析结果：抽样数据符合工序要求，进入下一步数据统计表单编号：说明：1.当PPK值<1.67时，请各相关单位讨论，并进行制程工序优化；2.抽样数据可在试产中的各阶段进行取样；3.产品正式量产前须完成此表单数据收集；经由各相关分析，会签；作为参数设置标准之依据。

竭诚为您提供优质文档/双击可除ppk,计算表格篇一：如何编写合格的cpk、ppk数据如何制作合格的“过程能力分析”ppk数据利用minitab软件（minitab16）生成假的合适的ppk 数据源—25组（每组5个）测量值。

要求计算得到的ppk值≥1.67。

以117.64±0.2为例。

一、打开minitab软件，选择“计算”-“随机数据”-“正态”（图1）二、在产生的（图2）对话框中填入数据。

“均值”为117.64；ppk为1.67时“标准差”等于单边公差0.2除于5得到值0.04；“数据行数”填125（25组/每组5个数据）；计划在表格中生成9组数据供挑选，表格每列的头部分别标记为1-9；在对话框左边选择全部列号码，点击选择后存入右边的框内。

点击确定后，得到数据如图3三、检验每列数据的ppk是否大于或等于1.67。

选择按钮“改善”-“评估能力”-“变量数据”-“正态能力”，见图4在出现的对话框中分别从左边选择一个列号码，如1；“子组大小”填5；“规格下限”和“规格上限”分别填下公差和上公差的数据。

见图5四、点确定后，出现一个图表（见图6），如果ppk≥1.67，则这组数据可用；如果ppk＜1.67，这组数据就放弃。

然后依次用“第三步”的方法检验1-9组数据哪几组可用。

五、在表格第一列前插入一列，循环往下填写1-5数字，一直到125行。

（见图7）六、拆分每列数据为5列。

选“数据”-“拆分列”（图8）在跳出的对话框内选择左边的列号码1到右边，“使用的下标”从左边选择c1列，在新的工作表中生成，点确定。

（图9）篇二：cpk与ppk的计算和评价等级过程能力计算及评价方法1.过程能力等级说明1.1cp评价等级——《质量专业理论与实务》（中级）1.2无偏时cp与合格（不合格）率的对应关系由上表可知，在无偏时cp与合格（不合格）率的对应关系是非线性的一一对应的关系，过程能力指数越大，合格率越高（反之亦然）。