(完整版)初一有理数混合运算思维导图
- 格式:doc
- 大小:53.01 KB
- 文档页数:2

1有理数航识导知1.正数与负数2.有理数3.数轴4.相反数5.绝对值6.倒数,负倒数思维脑图预习笔记正数与负数。
1.0。
、3、1、+0.3327%等数叫做正数。
正数都大于正数:像。
负数:正数前面加上“-”(读做负)的数,叫负数。
负数都小于0 即不是正数也不是负数。
0:如果正数表示某种意义,那么负数表示它相反意义,反用正负数表示相反意义的量之亦然。
相反意义的量包括两个方面的含义,一是相反意义;一是相反意义基础上要有量。
2. 有理数。
有理数:整数和分数统称有理数。
注:(1)正数和零统称非负数(2)负数和零统称非正数(3)正整数和零统称非负数(4)负整数和零统称非正整数3. 数轴。
数轴:规定原点正方向和单位长度的直线。
有理数与数轴上点的关系:一切有理数都可以用数轴上的点表示出来,在数轴上,右边的点所对应的数总比在左边的点对应的数大。
正数都大于0,负数都小于0,正数大于一切负数。
注意数轴上的点不都代表有理数,如:相反数。
4.的相反数为0。
相反数:只有符号不同的两个数互称相反数。
特别的,0 5. 绝对值。
,记作数轴上表示与原点的距离叫数的绝对值 6. 倒数,负倒数。
的两个数互为倒数。
,互为倒数,则,反之则亦然。
:乘积为倒数1没0,倒数是成对出现的,单独一个数不能称为倒数,互为倒数的两个数乘积一定是1 有倒数。
,互为倒数,则,,反之则亦然。
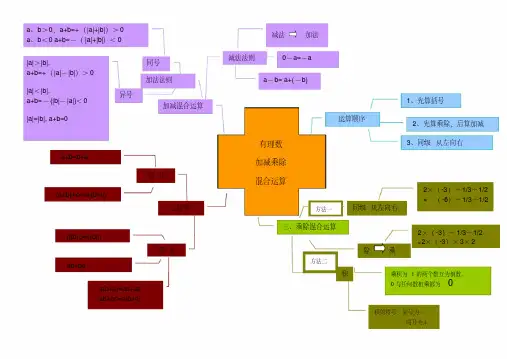
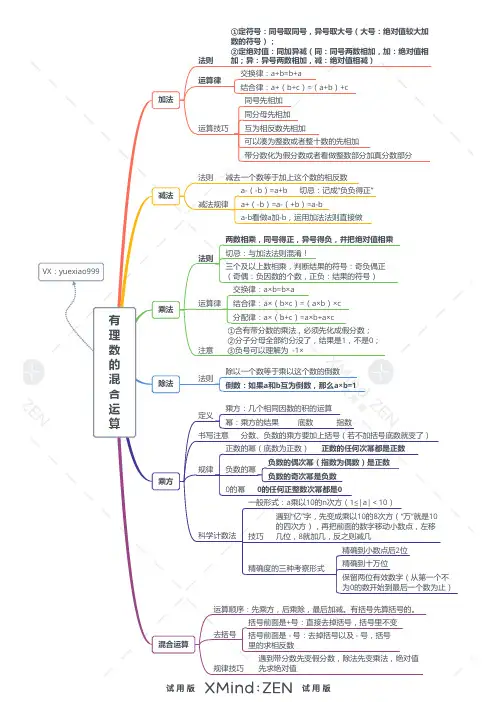
的两个数互为负倒数,:乘积为-负倒数11让学习更有效思维脑图2思维脑图2 有理数的运算航识知导1. 有理数的加法。
2. 有理数乘法。
有理数除法。
3.有理数的乘方。
4.5. 有理数混合运算。
3让学习更有效预习笔记有理数的加法。
1.有理数的加法法则。
、求和的绝对值、确定符号 2有理数的加法运算步骤:1 :运算技巧、分数与小数均有时,应化为统一形式;1 、带分数可分为整数与分数两部分参与运算;2 3、多个数相加时,若有互为相反数的两个数,可先结合相加得零; 4、若有可以凑整的数,即相加得整数,可先结合相合相加; 5、若有同分母的分数或易通分的分数,应先结合在一起;6、符号相同的数可以结合在一起。
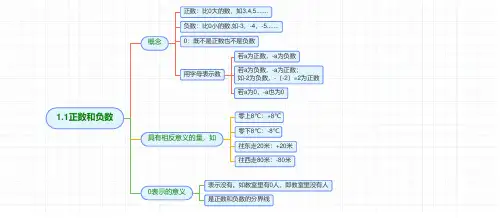
1.1正数和负数概念正数:比0大的数,如3,4,5.......负数:比0小的数,如-3,-4,-5.......0:既不是正数也不是负数用字母表示数若a为正数,-a为负数若a为负数,-a为正数;如-2为负数,-(-2)=2为正数若a为0,-a也为0具有相反意义的量,如零上8℃:+8℃零下8℃:-8℃往东走20米:+20米往西走80米:-80米0表示的意义表示没有。
如教室里有0人,即教室里没有人是正数和负数的分界线1.2有理数1.2.1有理数按意义分整数正整数负整数分数正分数负分数按性质符号分正有理数正整数正分数负有理数负整数负分数1.2.2数轴有原点、正方向、单位长度的一条直线任何有理数都能找到一个点与之对应,右边的数大于左边的数两点间距离:右边点对应的数减左边点对应的数1.2.3相反数只有符号不相同的两个数字互为相反数,a的相反数记为-a0的相反数是0,正数的相反数为负,负数的相反数为正一个数和它的相反数关于原点对称互为相反数的两个数相加等于01.2.4绝对值数轴上表示数a的点与原点的距离叫做数a 的绝对值,写为|a|互为相反数的两个数:绝对值相等两个负数,绝对值大的反而小,绝对值小的反而大若a>0,则|a|=a;若a<0,则|a|=-a;|0|=01.3有理数的加减法1.3.1加法同号两数相加:取相同的符号,绝对值相加;如-3+(-4)=-7异号两数相加:谁绝对值大,就取谁的符号;再用大绝对值减小绝对值;如-5+3=-2互为相反数的两数相加得0,任何数加0等于它本身1.3.2减法减去一个数,等于加上这个数的相反数;即a-b=a+(-b)如:5-(-3)=5+3=8加减混合相反数结合法:互为相反数的两个数相加等于0同分母结合法:把含相同分母的数或可通分的数结合在一起有带分数时先拆分为整数和分数,再结合分数和小数混合时统一为分数或统一为小数同号结合法:把符号相同的加数相结合(-23)-(-18)+(-15)-(+1)+(+23)原式=-23+(+18)+(-15)+(-1)+(+23)=(-23-25-1)+(18+23)=-7凑整法:把和为整数的加数相结合(+6.6)+(-5.2)-(-3.8)+(-2.6)-(+4.8)原式=(+6.6)+(-5.2)+(+3.8)+(-2.6)+(-4.8)=(6.6-2.6)+(-5.2-4.8)+3.8=-2.2分组结合法2-3-4+5+6-7-8+9…+66-67-68+69原式=(2-3-4+5)+(6-7-8+9)+…+(66-67-68+69)=0先拆项后结合(-2-4-6-8...-100)+(1+3+5+7 (99)原式=(-2+1)+(-4+3)+......+(-100+99)=-501.4有理数的乘除法1.4.1乘法两数相乘,同号得正,异号得负,并把绝对值相乘任何数乘0得0多个有理数相乘1.4.2除法除以一个数等于乘以这个数的倒数两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个非0数,等于0;0不能作除数只要一个因数为0则积为0如果因数都不是0,则结果符号根据负数的个数来定:奇负偶正1.5.1有理数的乘方求n个相同因数的积的运算,叫做乘方在aⁿ中,a 叫做底数,n 叫做指数。

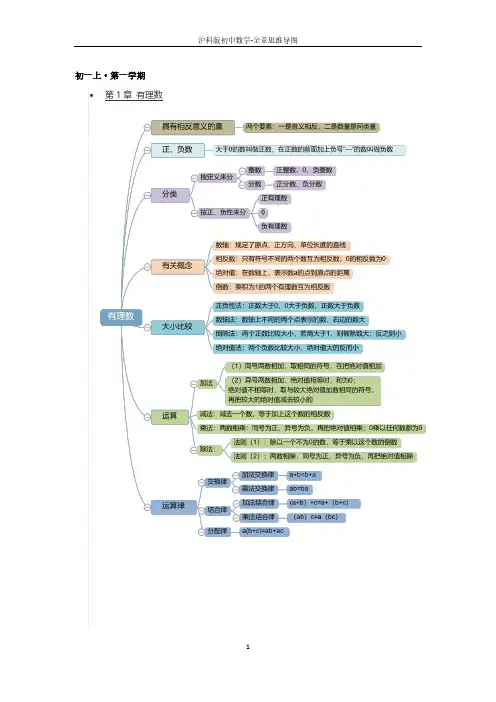
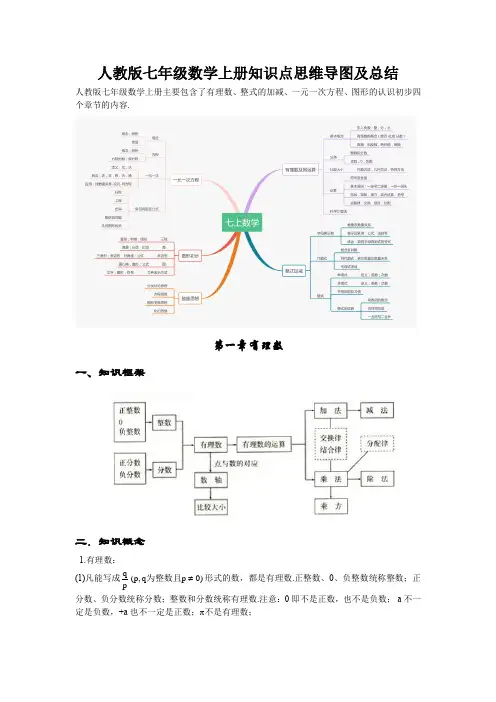
人教版七年级数学上册知识点思维导图及总结 人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a -b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b -a)n , 当n 为正偶数时: (-a)n =a n 或 (a -b)n =(b -a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版七年级数学上册章节思维导图
共4章
人教版七年级数学上册教材目录
第1章有理数的思维导图
1.1正数和负数
1.2有理数
1.3有理数的加减法
1.4有理数的乘除法
1.5有理数的乘方
第2章整式的加减的思维导图
2.1整式
2.2整式的加减
第3章一元一次方程的思维导图
3.1从算式到方程
3.2解一元一次方程(一)——合并同类项与移项
3.3解一元一次方程(二)——去括号与去分母
3.4实际问题与一元一次方程
第4章几何图形初步的思维导图
4.1几何图形
4.2直线、射线、线段
4.3角
4.4课题学习
设计制作长方体形状的包装纸盒。
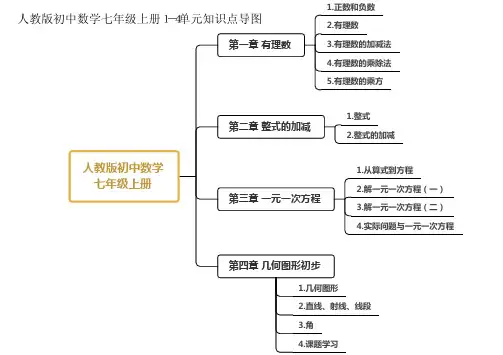
人教版初中数学七年级上册第一章 有理数第二章 整式的加减第三章 一元一次方程第四章 几何图形初步1.正数和负数2.有理数3.有理数的加减法4.有理数的乘除法5.有理数的乘方1.整式2.整式的加减1.从算式到方程2.解一元一次方程(一)3.解一元一次方程(二)4.实际问题与一元一次方程1.几何图形2.直线、射线、线段3.角4.课题学习人教版初中数学七年级上册1-4单元知识点导图正数和负数有理数有理数的加减法有理数的乘除法有理数的乘方0既不是正数也不是负数可以用来表示在一个问题中相反意义的量例如:一个物体向左移动记为+1m,向右移动记为-1m温度、海拔、收入增长...增长量是正数,表示真正的增长增长量是负数,表示负增长B.注意A.整数和分数统称为有理数整数分数正整数负整数正分数负分数能约分成整数的数不能算作分数两个整数的比、有限小数、无限循环小数都是分数无限不循环小数不是有理数(1)概念(2)三要素(3)画法画一条水平线,在直线上取一点表示0(这个点叫原点),选取某一长度作为单位长度,规定直线上向右的方向为正方向,这样的直线角数轴原点+正方向+单位长度A.画直线,定原点B.规定从原点向右为正方向,并用箭头表示C.根据需要选取适当长度D.标数(1)概念(2)注意像2和-2这样,只有符号不同的两个数叫做互为相反数A.“只有”就是说仅仅只有符号不同B.相反数是成对出现的C.一个数的相反数只有一个D.0的相反数是0(1)概念(2)注意数轴上表示a的点与原点的距离叫做数a的绝对值A.一个正数的绝对值是它本身B.一个负数的绝对值是它的相反数C.零的绝对值是零D.互为相反数的两个数的绝对值相等E.任何一个有理数的绝对值是非负数1.有理数加法法则2.有理数减法法则(1)同号两数相加,取相同的符号,并把绝对值相加(2)绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大绝对值减去较小绝对值(3)一个数同0相加,仍得这个数(4)互为相反数的两个数相加得0加法交换律加法结合律减去一个数等于加上这个数的相反数a-b=a+(-b)1.有理数乘法法则2.有理数除法法则(1)两数相乘,同号得正,异号得负,并把绝对值相乘(2)任何数与0相乘都得0(1)两数相除,同号得正,异号得负,并把绝对值相除(2)0除以任何一个不等于0的数,都得0(3)除以一个不等于0的数等于乘以这个数的倒数注意:A.乘积是1的两个数互为倒数B.几个不等于0的数相乘,积的符号由负因数的个数决定C.几个数相乘,有一个因数为0,积就为0奇数个--积为负偶数个--积为正1.乘方2.科学计数法3.近似数(1)概念(2)性质(3)运算求n个相同因数的积的运算,叫做乘方。
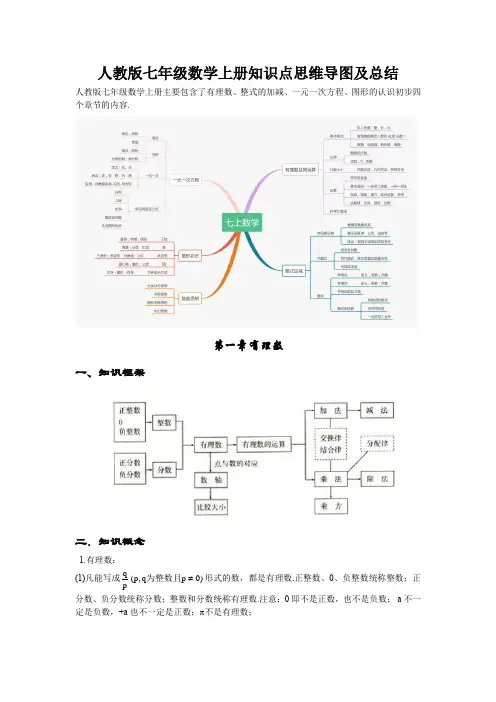
人教版七年级数学上册知识点思维导图及总结 人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a -b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b -a)n , 当n 为正偶数时: (-a)n =a n 或 (a -b)n =(b -a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
人教版七年级上册数学思维导图人教版七年级数学上册知识点思维导图及总结人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一、知识框架二.知识概念 1.有理数: (1)凡能写成q (p, q 为整数且 p ? 0) 形式的数,都是有理数.正整数、0、负整数统称整数;正 p 分数、负分数统称分数;整数和分数统称有理数.注意:0 即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;?不是有理数;(2)有理数的分类:? ?正整数 ?正有理数 ?正分数? ? ① 有理数 ?零 ? ?负整数 ?负有理数 ? ?负分数 ?? ?正整数 ?整数 ?零? ? ? ② 有理数 ? ?负整数 ? ?正分数 ?分数 ? ?负分数 ?2.数轴:数轴是规定了原点、正方向、单位长度的一条直线. 3.相反数: (1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0 的相反数还是 0; (2)相反数的和为 0 ? a+b=0 ? a、b 互为相反数. 4.绝对值: (1)正数的绝对值是其本身,0 的绝对值是 0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;?a (a ?0) (a ? 0) ? ?a (2) 绝对值可表示为: a ? ?0 (a ? 0) 或 a ? ? ;绝对值的问题经常分类讨论; ? a ( a ? 0) ? ? ? a ( a ? 0 ) ?5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比 0 大,负数永远比 0 小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数> 0,小数-大数< 0. 6.互为倒数:乘积为 1 的两个数互为倒数;注意: 0 没有倒数;若a≠0,那么 a 的倒数是1 ; a若 ab=1? a、b 互为倒数;若 ab=-1? a、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与 0 相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即 a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律:(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);(3)乘法的分配律:a(b+c)=ab+ac .即无意义 . 12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当 n 为正奇数时: (-a)n=-an 或(a -b)n=-(b-a)n , 当 n 为正偶数时: (-a)n =an 或 (a-b)n=(b-a)n . 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;a 0(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂; 15.科学记数法:把一个大于 10 的数记成a×10n 的形式,其中 a 是整数数位只有一位的数,这种记数法叫科学记数法. 16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位. 17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字. 18.混合运算法则:先乘方,后乘除,最后加减. 本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。