分数混合运算的整理与复习

第二单元《分数混合运算》整理与复习教学目标：1.梳理本单元知识点，整理有关分数混合运算顺序，运算定律以及分数在日常实际应用中的问题，帮助学生建立完整的知识体系。

2.通过不同形式的练习，分层次检验学生知识掌握情况，在练习中巩固强化，查漏补缺。

3.在解题过程中培养学生读题能力，提高学生分析、解决问题的能力。

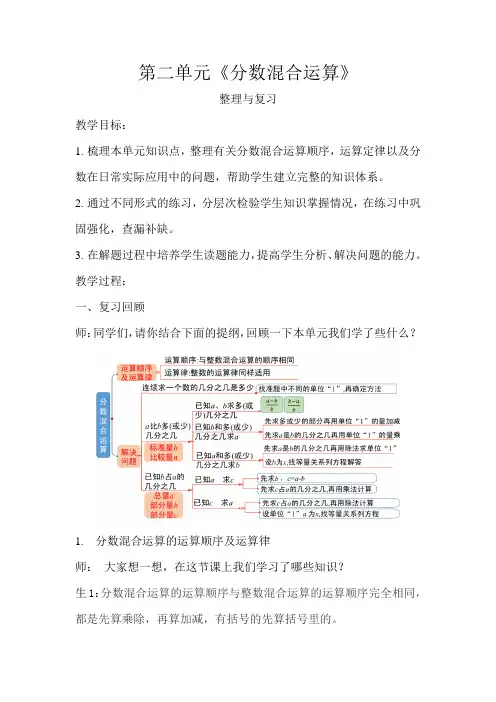
教学过程：一、复习回顾师：同学们，请你结合下面的提纲，回顾一下本单元我们学了些什么？1.分数混合运算的运算顺序及运算律师：大家想一想，在这节课上我们学习了哪些知识？生1：分数混合运算的运算顺序与整数混合运算的运算顺序完全相同，都是先算乘除，再算加减，有括号的先算括号里的。

①如果是同一级运算，按照从左到右的顺序依次计算。

②如果是分数连乘，可先进行约分，再进行计算；③如果是分数乘除混合运算时，要先把除法转换成乘法，然后按乘法运算。

生2：分数混合运算的运算律与整数混合运算的定律相同。

2.分数的解决问题师：你们记得真不错。

那么，谁来再说一说关于分数解决问题这一节课，我们学了哪些知识？生：用分数运算解决“求比已知量多（或少）几分之几的量是多少”的实际问题，方法是：可以先求出多或少的具体量，再用单位“1”的量加或减去多或少的部分，求出要求的问题。

生2：“已知甲与乙的和，其中甲占和的几分之几，求乙数是多少？”首先明确谁占单位“1”的几分之几，求出甲数，再用单位“1”减去甲数，求出乙数。

师：大家总结的都很到位，哪位同学还有补充?生3：解决分数问题时，也可以用方程来做具体步骤是：①要找准单位“1”。

②确定好其他量和单位“1”的量有什么关系，画出关系图，写出等量关系式。

③设未知量为x，根据等量关系式，列出方程。

④解答方程。

师：同学们，在交流中碰撞出了我们本单元的知识！我们的数学知识离不开生活，下面我们就要用我们本单元的知识来解决一些生活中的问题。

请看题。

设计意图：回顾梳理知识点，学生能明确这一单元所学到的知识点，使知识系统化。

分数混合运算知识点整理1、分数混合运算顺序与整数混合运算顺序相同，没有括号的先算(乘除)，再算(加减)；有括号的先算(括号里面的)，再算(括号外面的)。

2、整数的运算律在分数运算中同样适用。

加法运算定律：加法交换律：a+b=b+a 加法结合律：a+b+c=a+(b+c)乘法定律：乘法交换律：a x b=b x a 乘法结合律：a x b x c=a x (b x c) 乘法分配律：(a+b)x c=a x c+b x c 或a x c+b x c= (a+b)x c减法定律：减法的性质a-b-c=a-(b+c)或a-(b+c) =a-b-c除法的特性：a* b*c=a* (b x c)或a* (b x c)= a 宁b*c3、用方程解决有关分数混合运算的实际问题，关键是找出(单位1)，并把它设为未知数，再找出等量关系计算。

4、分数基本性质：分数的分子和分母同时乘以或除以相同的数( 0除外)分数的大小不变。

5、分数加减法同分母分数相加减，分母不变，分子相加减，异分母分数相加减，要先通分为同分母分数再相加减。

二、分数混合运算的应用1、打折计算方法：现价*原价二折扣2、一件商品打几折，求现价。

计算方法：原价x折数3、一件商品打几折，求原价。

计算方法：现价*折数4、分数混合运算的应用题解答方法解答方法：1、找准单位1——并在题目的文字下面标注①总数量是单位“T例如：小红看完整本书的，那么单位“1”是整本书的页码。

②原价就是单位“T例如：笔记本电脑原价是300元，现在降价了，那么单位“1”是原价3000元③分数比率之前的“的”字前面的量是单位“1”例如：全校男生的人数是女生人数的几分之几，那么单位“1”是女生人数。

④一个东西比另一个东西多几分之几中“比”后面的东西是单位“1”例如：商店卖的苹果比橘子多，那么单位“1”是橘子数量。

2、确定乘或除（1）已知单位“1”，用乘法（2）未知单位“1”，用除法或方程3、对应量和对应分率（1）单位“1”x对应分率（2）对应量十对应分率二单位“1”若用方程：一般设单位“1”的量为未知数4、如何根据分率句来写等量关系找出关键性的字和词，“是”字、“占”字、“相当于”、“正好是”等字、词, 相当于等量关系式中的等于号，分率前面的“的”字相当于等量关系式中的乘号。

“分数混合运算”知识整理一、分数混合运算1、分数混合运算顺序与整数混合运算顺序相同，没有括号的先算（乘除），再算（加减）;有括号的先算（括号里面的），再算（括号外面的）。

2、整数的运算律在分数运算中同样适用。

加法运算定律：加法交换律：a+b=b+a 加法结合律：a+b+c=a+(b+c)乘法定律：乘法交换律：a×b=b×a 乘法结合律：a×b×c=a×(b×c)乘法分配律：（a+b）×c=a×c+b×c或a×c+b×c=（a+b）×c减法定律：减法的性质a-b-c=a-(b+c)或a-(b+c) =a-b-c除法的特性：a÷b÷c=a÷(b×c)或a÷(b×c)= a÷b÷c3、用方程解决有关分数混合运算的实际问题，关键是找出（单位1），并把它设为未知数，再找出等量关系计算。

4、分数基本性质：分数的分子和分母同时乘以或除以相同的数（0除外）分数的大小不变。

5、分数加减法同分母分数相加减，分母不变，分子相加减，异分母分数相加减，要先通分为同分母分数再相加减。

二、分数混合运算的应用1、打折计算方法：现价÷原价=折扣2、一件商品打几折，求现价。

计算方法：原价×折数3、一件商品打几折，求原价。

计算方法：现价÷折数4、分数混合运算的应用题解答方法解答方法：1、找准单位1——并在题目的文字下面标注①总数量是单位“1”例如：小红看完整本书的 2/5，那么单位“1”是整本书的页码。

②原价就是单位“1”例如：笔记本电脑原价是300元，现在降价了 1/6，那么单位“1”是原价3000元。

③分数比率之前的“的”字前面的量是单位“1”例如：全校男生的人数是女生人数的4/5 ，那么单位“1”是女生人数。

六年级上册数学教案《分数混合运算》整理复习人教新课标教学内容本节课的内容是对六年级上册数学课程中“分数混合运算”的整理复习。

主要复习内容包括：1. 分数四则运算：回顾分数的加、减、乘、除运算规则，以及如何应用这些规则解决实际问题。

2. 分数与整数的混合运算：探讨分数与整数在四则运算中的混合使用，以及运算的优先级。

3. 运算顺序和法则：复习运算的顺序和法则，特别是在含有括号的表达式中如何正确计算。

教学目标1. 知识与技能：学生能够熟练掌握分数的四则运算，包括分数与整数的混合运算，并能够正确应用运算顺序和法则。

2. 过程与方法：通过复习和练习，学生能够提高解决分数混合运算问题的能力，培养逻辑思维和计算能力。

3. 情感态度与价值观：培养学生对数学学习的兴趣，提高其面对复杂问题的耐心和解决问题的信心。

教学难点1. 分数与整数混合运算的优先级：学生在处理分数与整数混合运算时，可能会对运算的优先级感到困惑。

2. 正确运用运算顺序和法则：在复杂的表达式中，学生可能会忘记或错误地应用运算顺序和法则。

教具学具准备1. 教具：黑板、粉笔、教学PPT、计算器。

2. 学具：练习本、铅笔、橡皮、直尺。

教学过程1. 复习导入：通过简单的练习题，复习分数的四则运算规则。

2. 重点讲解：讲解分数与整数混合运算的优先级，以及运算顺序和法则。

3. 实例演示：通过具体的例题，演示如何正确进行分数混合运算。

4. 课堂练习：让学生独立完成练习题，巩固所学知识。

板书设计1. 分数四则运算规则：列出分数加、减、乘、除的运算规则。

2. 分数与整数混合运算：示例展示分数与整数混合运算的解题步骤。

3. 运算顺序和法则：明确运算的优先级和顺序，特别是括号的使用。

作业设计1. 必做题：设计基础练习题，巩固分数混合运算的基本规则。

2. 选做题：设计一些挑战性的题目，让学生在掌握基础知识的基础上进行拓展和提高。

课后反思教学难点详细补充和说明1. 分数与整数混合运算的优先级在分数与整数混合运算中，学生可能会对运算的优先级感到困惑，特别是在包含多种运算符的表达式中。

分数混合运算笔记整理一、分数混合运算的顺序。

1. 没有括号的情况。

- 先算乘除，后算加减。

例如：计算(1)/(2)+(2)/(3)×(3)/(4)，先算乘法(2)/(3)×(3)/(4)=(1)/(2)，再算加法(1)/(2)+(1)/(2) = 1。

2. 有括号的情况。

- 先算括号里面的，再算括号外面的。

例如：计算((1)/(2)-(1)/(3))÷(1)/(6)，先算括号里的(1)/(2)-(1)/(3)=(3 - 2)/(6)=(1)/(6)，再算除法(1)/(6)÷(1)/(6)=1。

二、分数混合运算中的简便运算。

1. 乘法分配律的应用。

- 对于式子a×(b + c)=a× b+a× c，在分数运算中同样适用。

例如：(1)/(2)×((2)/(3)+(4)/(5))=(1)/(2)×(2)/(3)+(1)/(2)×(4)/(5)=(1)/(3)+(2)/(5)=(5 +6)/(15)=(11)/(15)。

- 有时候需要将式子变形后才能使用乘法分配律。

例如：(3)/(4)×(5)/(6)+(3)/(4)×(1)/(6)=(3)/(4)×((5)/(6)+(1)/(6))=(3)/(4)×1=(3)/(4)。

2. 乘法交换律和结合律的应用。

- 乘法交换律a× b = b× a，乘法结合律(a× b)× c=a×(b× c)。

例如：计算(1)/(3)×(2)/(5)×3，根据乘法交换律(1)/(3)×3×(2)/(5)=1×(2)/(5)=(2)/(5)。

三、解决分数混合运算的实际问题。

1. 审题。

- 认真读题，找出题目中的关键信息，确定已知量和未知量。

第五单元分数四则混合运算知识点整理
1、分数四则混合运算的顺序
分数四则混合运算运算的顺序，和整数、小数四则混合运算顺序相同。

先算乘除法，后算加减法；有括号的先算小括号里面的，再算中括号，最后算括号外面的。

2、分数四则混合运算的运算律
（注：如果遇到除法，先转化为乘法，再使用运算律）
加法的交换律：a＋b = b＋a
加法的结合律：(a＋b)＋c = a＋(b＋c)
减法的性质：a－(b＋c) = a－b－c
a－(b－c) = a－b＋c
乘法的交换律：a×b = b×a
乘法的结合律：(a×b)×c = a×(b×c)
乘法的分配律：(a＋b)×c = a×c＋b×c
(a－b)×c = a×c－b×c
减法的性质：a÷(b×c) = a÷b÷c
a÷(b÷c) = a÷b×c
3、稍复杂的分数乘法实际问题
（1）总数与部分数相比较的问题：【分数乘法、减法】
一般解题方法：先求出未知的部分数，再用总数减部分数等于另一部分数。

（2）已知一个数量比另一个数量多（或少）几分之几，求这个数量是多少的问题：【分数乘法、加减法】
一般解题方法：先求出多（或少）的部分，再用加法或减法求出结果。

（注：1、对于题中出现的带单位与不带单位的分数，要注意它们的意义不一样。

2、看清单位“1”，看清已知分率对应的是什么量。

）。

《分数混合运算》复习知识点分数混合运算知识点
1、分数混合运算顺序与整数混合运算顺序相同。

2、整数运算定律在分数运算中同样适用。

3、分数混合运算的应用;利用方程来解决某些实际问题。

练习题
1、40的14是，比0少14是，20比多14。

2、一种混凝土沙子3份，石子2份，水泥1份拌在一起，沙子占混凝土的，石子比沙子少
3、一儿童服装原价200元，打八折后现价是元。

现价比原价便宜元。

参考答案
1、40的1/4是，比0少1/4是，20比多1/4。

2、一种混凝土沙子3份，石子2份，水泥1份拌在一起，沙子占混凝土的，石子比沙子少
3、一儿童服装原价200元，打八折后现价是元。

现价比原价便宜元。

分数混合运算知识点整理1、分数混合运算顺序与整数混合运算顺序相同，没有括号的先算（乘除），再算（加减）;有括号的先算（括号里面的），再算（括号外面的）。

2、整数的运算律在分数运算中同样适用。

加法运算定律：加法交换律：a+b=b+a 加法结合律：a+b+c=a+(b+c)乘法定律：乘法交换律：a×b=b×a 乘法结合律：a×b×c=a×(b×c) 乘法分配律：（a+b）×c=a×c+b×c或a×c+b×c=（a+b）×c减法定律：减法的性质a-b-c=a-(b+c)或a-(b+c) =a-b-c除法的特性：a÷b÷c=a÷(b×c)或a÷(b×c)= a÷b÷c3、用方程解决有关分数混合运算的实际问题，关键是找出（单位1），并把它设为未知数，再找出等量关系计算。

4、分数基本性质：分数的分子和分母同时乘以或除以相同的数（0除外）分数的大小不变。

5、分数加减法同分母分数相加减，分母不变，分子相加减，异分母分数相加减，要先通分为同分母分数再相加减。

二、分数混合运算的应用1、打折计算方法：现价÷原价=折扣2、一件商品打几折，求现价。

计算方法：原价×折数3、一件商品打几折，求原价。

计算方法：现价÷折数4、分数混合运算的应用题解答方法解答方法：1、找准单位1——并在题目的文字下面标注①总数量是单位“1”例如：小红看完整本书的，那么单位“1”是整本书的页码。

②原价就是单位“1”例如：笔记本电脑原价是300元，现在降价了，那么单位“1”是原价3000元。

③分数比率之前的“的”字前面的量是单位“1”例如：全校男生的人数是女生人数的几分之几，那么单位“1”是女生人数。

④一个东西比另一个东西多几分之几中“比”后面的东西是单位“1”例如：商店卖的苹果比橘子多，那么单位“1”是橘子数量。

分数混合运算知识点整理1、分数混合运算顺序与整数混合运算顺序相同,没有括号的先算乘除,再算加减;有括号的先算括号里面的,再算括号外面的;2、整数的运算律在分数运算中同样适用;加法运算定律：加法交换律：a+b=b+a 加法结合律：a+b+c=a+b+c乘法定律：乘法交换律：a×b=b×a乘法结合律：a×b×c=a×b×c乘法分配律：a+b×c=a×c+b×c或a×c+b×c=a+b×c减法定律：减法的性质a-b-c=a-b+c或a-b+c =a-b-c除法的特性：a÷b÷c=a÷b×c或a÷b×c= a÷b÷c3、用方程解决有关分数混合运算的实际问题,关键是找出单位1,并把它设为未知数,再找出等量关系计算;4、分数基本性质：分数的分子和分母同时乘以或除以相同的数0除外分数的大小不变;5、分数加减法同分母分数相加减,分母不变,分子相加减,异分母分数相加减,要先通分为同分母分数再相加减;二、分数混合运算的应用1、打折计算方法：现价÷原价=折扣2、一件商品打几折,求现价; 计算方法：原价×折数3、一件商品打几折,求原价; 计算方法：现价÷折数4、分数混合运算的应用题解答方法解答方法：1、找准单位1——并在题目的文字下面标注①总数量是单位“1”例如：小红看完整本书的 ,那么单位“1”是整本书的页码;②原价就是单位“1”例如：笔记本电脑原价是300元,现在降价了 ,那么单位“1”是原价3000元; ③分数比率之前的“的”字前面的量是单位“1”例如：全校男生的人数是女生人数的几分之几 ,那么单位“1”是女生人数; ④一个东西比另一个东西多几分之几中“比”后面的东西是单位“1” 例如：商店卖的苹果比橘子多 ,那么单位“1”是橘子数量; 2、确定乘或除1已知单位“1”,用乘法 2未知单位“1”,用除法或方程3、对应量和对应分率1单位“1”×对应分率2对应量÷对应分率=单位“1”若用方程：一般设单位“1”的量为未知数4、如何根据分率句来写等量关系找出关键性的字和词,“是”字、“占”字、“相当于”、“正好是”等字、词,相当于等量关系式中的等于号,分率前面的“的”字相当于等量关系式中的乘号; 如：1公鸡的只数是“是”可以改为“占”或“相当于”、或“正好是”等字词母鸡的 ;等量关系式是：母鸡的只数× =公鸡的只数2五年级有男生15人,相当于“相当于”可以改为“是”或、“占”或“正好是”等字、词;全班人数的几分之几 ;数量关系式是：全班人数×几分之几 =男生人数分数混合运算练习题姓名： 班级：一、 填空1、一根绳子长2米,剪去52,还剩 米,如果剪去52米,还剩 米;2、20千克增加它的41是 千克,20千克比25千克少 ,25千克比20千克多 ;3、一袋米50千克,卖掉了 千克,还剩它的52; 4、一段路修了83后,还剩下1000米没修,这段路共有 米; 5、小明5天看了一本书的41,他平均每天看这本书的 ,照这样的速度,他看完这本书要 天;6、90比100少 ,80比60多 ;填分数7、一本书,每天看它的71, 天可以看完; 8、一箱苹果,吃了52,吃了18个,这箱苹果原有 个; 9、甲数是25,乙数的41等于甲数的52,乙数是 ; 二、应用题1、一辆汽车从甲地开往乙地,全程600千米,已经行驶了全程的52,离乙地还有多少米2、海京居有40户人家,海星阁比海京居多83,海星阁有多少户人家3、鲜鲜水果店运进30筐苹果,第一天卖出总数的51,第二天卖出总数的21,两天共卖出水果多少筐4、鲜鲜水果店运进一批水果,第一天卖出总数的41,第二天卖出总数的51,两天一共卖出水果90千克,这批水果共重多少千克5、同学们收集废电池,五年级收集了280个,比四年级多41,四年级收集了多少个6、工程队修一段路,第一天修了全长的51,第二天修了200米,两天刚好修了全长的一半,这段路一共有多少米7、小明看一本书,已经看了150页,还剩下全书的83没看,全书有多少页8、一台空调原价是3000元,先涨价101,后又降价101卖出,这台空调现在的价钱是多少元9、合唱队有50人,舞蹈队的人数是合唱队的54,美术组的人数是舞蹈队的85,美术组有多少人。

分数四则混合运算的整理和复习教学设计The arrangement and review teaching design of the mixed operation of four fractions分数四则混合运算的整理和复习教学设计前言：小泰温馨提醒，数学是研究数量、结构、变化、空间以及信息等概念的一门学科，从某种角度看属于形式科学的一种，在人类历史发展和社会生活中，数学发挥着不可替代的作用，是学习和研究现代科学技术必不可少的基本工具。

本教案根据数学课程标准的要求和针对教学对象是小学生群体的特点，将教学诸要素有序安排，确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。

便于学习和使用，本文下载后内容可随意修改调整及打印。

教学内容教科书第1、2题，练习二十一的第1～3题．教学目的使学生能根据分数四则混合运算式题的具体情况，灵活运用各种简便算法，进一步提高计算能力．教学过程一、复习分数四则混合运算1．教师：我们已经学习了分数四则混合运算，谁能说说分数四则混合运算的顺序与整数四则混合运算的顺序是否相同？然后，让学生计算的第1题：＋×－÷［－（＋）］做完后，指名说一说计算的顺序．2．独立完成练习二十六第1题第一横行的第1、2小题．二、复习分数四则混合运算的简便运算1．教师出示第2题的前两题：×3＋×53×（＋）－让学生先想一想各题怎样计算比较简便，然后再计算．计算完后，指名学生说出各题是怎样计算的，在进行简便运算时，运用了什么运算定律．使学生认识到：第一小题运用乘法分配律，可以使计算简便；第二小题先运用乘法分配律把两个分数约分，再计算比较简便．2．让学生把第2题余下的两题做完，并说一说每一题是怎样使计算简便的．（第3小题先算出小括号里得，再用减．）三、课堂练习1．独立完成练习二十六的第2题．2．做练习二十六的第3题．先让学生自己做，订正时说一说各题解题的依据．如，5x－＝，先把看作减数，5x看作被减数，根据“被减数＝减数＋差”得到5x＝＋，再把＋看作积，x看作一个因数，根据“积÷一个因数＝另一个因数”得到x＝（＋）÷5，由此求出x的值．-------- Designed By JinTai College ---------。

分数混合运算复习与整理一、分数混合运算的顺序1、同级运算从左到右；2、两级运算，先算乘除，再算加减；3、有小括号又有中括号的，要先算小括号里面的再算中括号里面的，最后算括号外的。

【分数混合运算的顺序与整数混合运算的顺序相同。

】二、在分数四则混合运算的计算中应该注意什么？第一，要认真审题，首先要弄清运算顺序，明确先算什么，再算什么，最后算什么。

第二，要保证每一步计算准确无误。

第三，要注意不抄错数字符号等。

三、计算时的术语（1）分率：表示一个数是另一个数的几分之几，这几分之几通常称为分率。

（2）标准量：解答分数应用题时，通常把题目中作为单位“1”的那个数，称为标准量。

（3）比较量：解答分数应用题时，通常把题目中同标准量比较的那个数，称为比较量。

四、复习总结第一课总结：①除以一个数等于乘以这个数的倒数。

所以一般第一步先化÷为×。

②＋－注意通分。

③×注意分子和分母“逐个”约分。

④结果将假分数化成带分数。

第二课总结：整数中的运算律在分数中同样适用。

1）乘法分配律: （a+ b）×c=a×c+ b×c （2）乘法交换律:a×b=b×a（3）乘法结合律:a×b×c=a×(b×c)运用运算定律可对分数的混合运算进行简便运算。

第三课总结：求一个数的几分之几是多少，用乘法计算。

已知比较量和比较量比标准量多或少几分之几，求这个数，用除法计算，还可以用方程解答。

一、填空：1、分数混合运算中同级运算是按（先左后右）的顺序进行计算的。

2、分数混合运算中含两级运算的，是按先算（乘除），后算（加减）的顺序进行计算的。

3、分数混合运算中含有括号的，要先算（括号）里面的，再算（括号）外面的。

4、分数混合运算和整数四则混合运算的顺序是（一样）的。

六年级上册数学第六单元整理
六年级上册数学第六单元主要是关于分数混合运算的整理与复习。

这一单元主要包括以下几个方面：
● 1.分数混合运算的顺序：
分数混合运算的顺序与整数混合运算的顺序相同，先乘除后加减，有括号的先算括号里的运算。

● 2.解决问题：
1.在解决分数混合运算的问题时，需要先理解题目的意思，并找出相关的数学信息。

2.通常需要先列出方程或表达式，然后进行计算。

●分数与小数的互化：
分数可以转化为小数，小数也可以转化为分数。

●分数和小数互化的方法有：直接观察、利用分数性质、利用小数
性质等。

●简便运算：
利用运算律和运算性质进行简便运算，如乘法分配律、乘法结合律等。

●分数混合运算的应用：
通过解决实际问题，进一步巩固分数混合运算的知识，提高解决实际问题的能力。

在整理这一单元时，建议将重要的公式、定理、性质以及典型例题整
理在一起，方便记忆和应用。

同时，可以制作一些练习题进行巩固和提高。

如果有不明白的地方，可以向老师或同学请教。