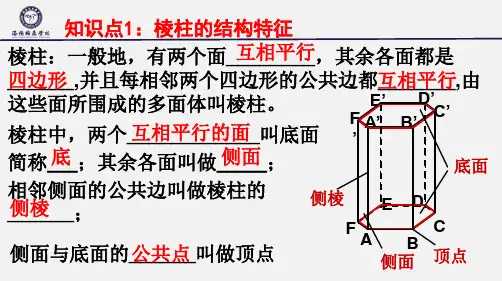
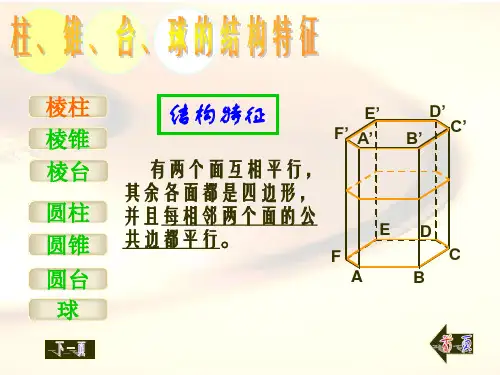
_三__角__形__
互相_平__行__ 延长线交于_一__点__
_梯__形__
2.旋转体的结构特征
名称
圆柱
圆锥
圆台
球
图形
母线
平行、相等且 _垂__直__于底面
相交于_一__点__
延长线交于_一__点__
轴截面 全等的_矩__形__
全等的_等__腰__三__ _角__形__
全等的_等__腰__梯__形__
1
的,长度变成本来的__2__.
4.三视图 几何体的三视图包括_主__视图、_左__视图、_俯__视图,分别是从几何体的正前方、 正左方和正上方视察几何体画出的轮廓线.
5.圆柱、圆锥、圆台的侧面展开图及侧面积公式
圆柱
圆锥
圆台
侧面 展开图
侧面积 公式
S圆柱侧=_2_π__r_l
S圆锥侧=_π__r_l
所以EF∥PB,且EF= 1 PB=x,
2
因为△ABC是边长为2的等边三角形,
所以CF= 3 ,又∠CEF=90°,所以CE= 3 x2,
AE= 1 PA=x,
2
在△AEC中,利用余弦定理得cos∠EAC=
x2 4 3 x2 ,作PD⊥AC于D,因为PA=PC,
22x
所以D为AC中点,cos∠EAC= AD 1 ,
2
提示:(1)×,也可以是棱台. (2)×,棱锥其余各面都是有同一个公共顶点的三角形. (3)×,侧棱延长后必须交于一点. (4)×,必须用平行于底面的平面去截棱锥. (5) ×,圆锥的三视图中,有两个三角形一个圆. (6) ×,锥体的体积等于底面积与高之积的三分之一. (7) √,正方体的体对角线是球的直径.
所以P-ABC为正方体一部分,2R= 2 2 2 6 ,