北师大八下第三章图形平移与旋转集体备课

第三章 图形的平移与旋转2.图形的旋转（二）本节课的主要内容是通过实例进一步认识旋转变换，探索、理解旋转的特征，并应用旋转的特征作图、解决简单的图形问题。

课前热身：1. 旋转的定义： 这个定点称为_____，转动的角称为____.旋转不改变图形的________.2.旋转的基本性质：对应点到旋转中心的距离对应点与旋转中心所连线段的夹角等于旋转前、后的图形图形的旋转是由 和旋转方向和旋转角度决定（注意：请准备好圆规、三角板、量角器和铅笔）3.关于点的旋转（1）点A 绕点O 逆时针旋转60° OA 4．关于线段的旋转（1）画出线段AB 绕着端点A 顺时针旋转60度后的线段（2）画出线段AB 绕着端点O 顺时针旋转90度后的线段 讲授新知：关于三角形的旋转类型一：已知旋转中心与旋转角作旋转后的图形例1.试着画△ABC 绕O 点逆时针旋转60°后所得的三角形．变式.如图，△ABC 绕O 点旋转后，顶点A 的对应点为点D ，试确定顶点B ，C 对应点的位置，以及旋转后的三角形A B B A O总结：“旋转”作图的步骤：一连：连接已知点与旋转中心二定：确定旋转方向三量：测量旋转角度四截：在旋转角的另一条边上，以旋转中心为一端点截取等于对应线段长度的线段五画：顺次连接所得的点，从而画出旋转得到的图形例2（格点问题）如图，正方形网格中，每个小正方形的边长都是1个单位长度，在平面直角坐标系中，△OAB 的三个顶点O（0，0），A（4,1），B（4,4）均在格点上画出△OAB绕原点O顺时针旋转90°后得到的△OA1B1，并写出点A1的坐标变式(坐标系中的旋转)如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么点A(－2，5)的对应点A′的坐标是________.类型二：已知旋转后的图形，反过来寻找旋转中心和旋转角的位置例1.如图，在方格纸上，△DEF是由△ABC绕定点P顺时针旋转得到的，如果用(2，1)表示方格纸上A点的位置，(1，2)表示B点的位置，那么点P的位置为（）A．(5，2)B．(2，5)C．(2，1)D．(1，2)变式：如图，四边形ABCD和四边形CDFE是边长相等的两个正方形，其中A、D、F 和B、C、E各成一直线，将正方形ABCD绕着一点旋转一定的角度后与正方形CDFE重合，这样的旋转中心共有多少个？确定旋转中心与旋转角的方法：在图形的旋转过程中，判断谁是旋转中心，要看旋转中心是在图形上还是不在图形上；若在图形上，哪一点在旋转过程中位置没有改变，这一点就是旋转中心；若不在图形上，对应点连线的垂直平分线的交点就是旋转中心，旋转角等于对应点与旋转中心所连线段的夹角．随堂练习：1.同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的．如图是在万花筒中看到的一个图案．图中所有小三角形均是全等的等边三角形，其中的四边形AEFG可以看成是四边形ABCD以A为旋转中心() A．顺时针旋转60°得到的B．顺时针旋转120°得到的C．逆时针旋转60°得到的D．逆时针旋转120°得到的2.如图，在4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心是()A．点A B．点B C．点C D．点D课堂小结课后作业：请完成《英才课堂》59~60页1~10题必做，11、12题选做。

第三章图形的平移与旋转1 图形的平移第2课时【教学目标】知识技能目标:通过“变化的鱼”探究横向(或纵向)平移一次,其坐标变化的规律,认识图形变换与坐标之间的内在联系. 过程性目标:在活动过程中,提高学生的探究能力和方法.情感态度目标:通过收集自己身边“平移”的实例,感受“生活处处有数学”,激发学生学习数学的兴趣;通过欣赏生活中平移图形与学生自己设计平移图案,使学生感受数学的美.【重点难点】重点:通过“变化的鱼”探究横向(或纵向)平移一次,其坐标变化的规律难点:坐标的变化与点的平移之间的关系【教学过程】一、创设情境图中的“鱼”是将坐标为(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)的点用线段依次连接而成的,将这条“鱼”向右平移5个单位长度.(1)画出平移后的新“鱼”.(2)在图中尽量多选取几组对应点,并将它们的坐标填入下表:原来的“鱼”( , ) ( , ) ( , ) …向右平移5个单位长度后的( , ) ( , ) ( , ) …新“鱼”(3)你发现对应点的坐标之间有什么关系?如果将原来的“鱼”向左平移4个单位长度呢?请你先想一想,然后再具体做一做.二、探究归纳活动一:探求坐标系中的平移变换想一想:如果将图中的“鱼”向上平移3个单位长度,那么平移前后的两条“鱼”中,对应点的坐标之间有什么关系?如果将图中的“鱼”向下平移2个单位长度呢?做一做:(1)将图中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别加3,再将得到的点用线段依次连接起来,从而画出一条新“鱼”,这条新“鱼”与原来的“鱼”相比有什么变化?如果纵坐标保持不变,横坐标分别减2呢?(2)将图中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别加3,所得到的新“鱼”与原来的“鱼”相比又有什么变化?如果横坐标保持不变,纵坐标分别减2呢?例题讲解议一议:在平面直角坐标系中,一个图形沿x轴方向平移a(a>0)个单位长度后的图形与原图形对应点的坐标之间有什么关系?如果图形沿y轴方向平移a(a>0)个单位长度呢?与同伴交流.归纳总结如下:1.一个图形沿x轴方向平移a(a>0)个单位长度:(x,y)向右平移a个单位(x+a,y)向左平移a个单位(x-a,y)2.一个图形沿y轴方向平移a(a>0)个单位长度:(x,y)向上平移a个单位(x,y+a)向下平移a个单位(x,y-a)三、交流反思通过一条“鱼”的平移,探究“鱼”横向或纵向平移一次的坐标变化,进一步感受平移的实质,渗透平移的三要素,即“基本图形、方向、距离”.操作性强又富有挑战性的数学活动,激发了学生学习的兴趣,对平移的基本内涵和基本性质这两个重点,学生掌握得比较好.四、检测反馈1.四边形ABCD的顶点坐标分别是A(0,3),B(-3,0),C(0,-3),D(3,0)(1)将四边形ABCD向右平移6个单位长度,得到四边形A1B1C1D1,写出四边形A1B1C1D1各顶点的坐标;(2)将四边形A1B1C1D1向上平移6个单位长度,得到四边形A2B2C2D2,写出四边形A2B2C2D2各顶点的坐标.2.(1)将第1题中的四边形A2B2C2D2各顶点的纵坐标不变,横坐标分别减4,得到四边形A3B3C3D3,它与四边形A2B2C2D2相比有什么变化?(2)将四边形A3B3C3D3各顶点的横坐标不变,纵坐标分别减4,得到四边形A4B4C4D4,它与四边形A3B3C3D3相比有什么变化?五、布置作业.课本P70 3.2习题六、板书设计七、教学反思1.注意学生活动的指导教师应对小组讨论给予适当的指导,包括知识的启发引导、学生交流合作中注意的问题及对困难学生的帮助等,使小组合作学习更具实效性.在小组讨论之前,应该留给学生充分的独立思考的时间,不要让一些思维活跃的学生的回答代替了其他学生的思考,掩盖了其他学生的疑问.2.给学生空间最后提出的一个挑战性问题,虽不能解决,让学生更加急迫地要充实新知识解决未解决的问题,从而使自己获得更大的成功,以成良性循环的学习模式.。

北师大版本八年级数学下第三章图形的平移与旋转章末复习教案课标要求【知识与技能】1.平移的基本涵义及其性质；2.旋转的基本涵义及其性质；3.能按要求作出简单平面图形平移后或旋转后的图形；4.图形之间的变换关系；5.运用轴对称、平移和旋转的组合进行图案设计.【过程与方法】通过回顾进一步理解平移、旋转的基本性质，并能准确作出简单平面图形平移、旋转后的图形.【情感态度】通过回顾与思考，进一步发展学生的空间观念，培养其操作技能，增强审美意识.【教学重点】理解平移、旋转与中心对称的概念和性质.掌握坐标系中平移、对称的坐标特征【教学难点】灵活运用平移、旋转与中心对称的概念和性质解决相关图形问题教学过程一.知识结构【教学说明】引导学生回顾本章知识点，使学生系统地了解本章知识及它们之间的关系.二.释疑解惑，加深理解1.平移平移的概念：在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移.平移的性质：平移不改变图形的形状和大小；图形经过平移，连接各组对应点所得的线段互相平行且相等.2.旋转旋转的概念：把一个图形绕一个定点转动一定的角度，这样的图形运动叫做旋转，这个定点叫做旋转中心，旋转的角度叫做旋转角.旋转的性质：旋转前、后的图形全等；对应点到旋转中心的距离相等；每一对对应点与旋转中心的连线所成的角彼此相等.3.轴对称如果一个图形沿一条直线折叠后，直线两旁的部分能够重合，那么这个图形叫做轴对称图形.4.中心对称与中心对称图形中心对称与中心对称图形的联系与区别：区别: 中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.联系: 如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形.如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.二．通过四个考点知识的训练，巩固所学知识。

学生在教师的引导下分析问题，解决问题。

考点一：平移1. 下列运动属于平移的是( )A．急刹车时汽车在地面上的滑动B．投篮时的篮球运动C．冷水加热过程中小气泡上升成为大气泡D．随风飘动的树叶在空中的运动2. 将点A(1，－1)向上平移2个单位后，再向左平移3个单位，得到点B，则点B的坐标为( )A．(－2，1) B．(－2，－1) C．(2，1) D．(2，－1)3. 如图，点A，B的坐标分别为(1，2)，(4，0)，将△AOB沿x轴向右平移，得到△CDE，已知DB＝1，则点C的坐标为________．4. 如图，将△ABC向左平移4个单位，再向下平移2个单位得到△A′B′C′.(1)画出△A′B′C′的图形；(2)若点P(a，b)是△ABC内部一点，则平移后△A′B′C′内的对应点P′的坐标为(a－4，b－2)；(3)求△ABC的面积．考点二：旋转5. 将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是( )6. 如图，BA＝BC，∠ABC＝70°，将△BDC绕点B逆时针旋转至△BEA 处，点E，A分别是点D，C旋转后的对应点，连接DE，则∠BED为( ) A．55°B．60°C．65°D．70°7. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(－3，5)，B(－2，1)，C(－1，3)．(1)若△ABC关于x轴对称的图形是△A1B1C1，直接写出点A1，B1，C1的坐标；(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2，画出△A2B2C2，并写出A2的坐标．考点三：中心对称9. 下列图形中是中心对称图形的是( )10. 如图，△ABC与△A′B′C′关于点O成中心对称，∠ABC＝45°，∠B′C′A′＝80°，∠BAC＝_______°.考点四：图案设计11. 如图的四个图形中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有( )A ．1个 B ．2个 C ．3个 D ．4个12.如图3，两个相同的正方形纸片ABCD 和EFGH ，边长为m ，将纸片EFGH 的一个顶点E ，放在纸片ABCD 对角线的交点O 处，那么正方形纸片EFGH 绕点O 无论怎样旋转，两个正方形纸片重叠部分的面积等于______.1【教学说明】应用平移、旋转，中心对称，团案设计解决实际问题，增强了学生应用数学的意识，让学生总结学习到的思想方法，培养学生的综合能力. 五.师生互动，课堂小结图形的中心对称、平移、旋转是几何中的重要概念，应用中心对称、平移、旋转解题也是一种极为重要的数学思想方法，适当地应用中心对称、平移、旋转等方法，将那些分散、远离的条件从图形的某一部分转移到适当的新的位置上，E ()O H GFDCBA 图E ()OHGFD C BA图2图3NM E ()O HGFDC B A集中、汇集已知条件和求证结论，发现、拓展解题思路，构造基础三角形，进行计算与证明.课后作业布置作业:教材“复习题”中第2、5、7、9题.教学反思本节突出平移与旋转概念加深理解和性质应用探究活动的教学.首先分析图形的变换、平面直角坐标系中的平移旋转方面帮助学生把握概念的本质特征，以培养学生观察、分析的能力，再引导学生运用性质解决数学问题和实际问题，由浅入深，培养学生应用数学知识分析、解决问题的能力.。

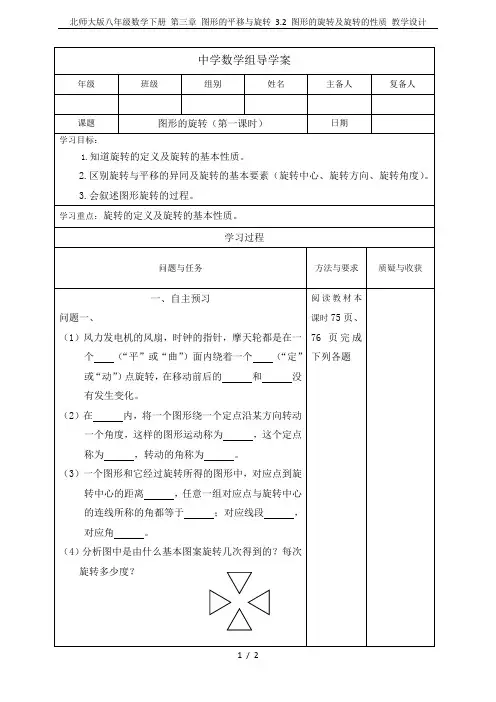
中学数学组导学案年级班级组别姓名主备人复备人课题图形的旋转（第一课时）日期学习目标：1.知道旋转的定义及旋转的基本性质。

2.区别旋转与平移的异同及旋转的基本要素（旋转中心、旋转方向、旋转角度）。

3.会叙述图形旋转的过程。

学习重点：旋转的定义及旋转的基本性质。

学习过程问题与任务方法与要求质疑与收获一、自主预习问题一、（1）风力发电机的风扇，时钟的指针，摩天轮都是在一个（“平”或“曲”）面内绕着一个（“定”或“动”）点旋转，在移动前后的和没有发生变化。

（2）在内，将一个图形绕一个定点沿某方向转动一个角度，这样的图形运动称为，这个定点称为，转动的角称为。

（3）一个图形和它经过旋转所得的图形中，对应点到旋转中心的距离，任意一组对应点与旋转中心的连线所称的角都等于；对应线段，对应角。

（4）分析图中是由什么基本图案旋转几次得到的？每次旋转多少度？阅读教材本课时75页、76页完成下列各题问题二、 如图所示，△AOB 与△ABC 绕O 点旋转得到△COD 与△DEF ，在这个旋转过程中： （1）旋转中心是什么？旋转角是什么？（2）经过旋转，点A ，B 分别移动到了什么位置？ （3）图（1）中AO 与CO 长有什么关系？图（2）中AO 与DO 长有什么关系？（4）图（1）中∠AOC 与∠BOD 大小有何关系图（2）中∠AOD 与∠COF 大小有何关系？ （5）你还能找到这两幅图中其他线段和角的大小关系吗？小组合作，教师引导完成二、合作展示1、组内交流：（1）你在预习中有什么困惑？还有哪些解决不了的问题在小组内交流解决。

（2）组长汇总本组出错较多问题和解决不了的问题。

2、班内展示：谁能解决以上问题，请将思考过程、解题步骤展示给全班同学。

大胆、大声、大方三、检测反馈课本76页随堂练习独立完成，教师讲解 四、反思提升（1）通过本节课的学习，你学会了哪些知识； （2）通过本节课的学习，你收获了什么数学方法？ 班内交流OABDO BAC EDF。

图形的旋转变换——“点”的思考
教材分析：本章在学生学习了轴对称变换之后，初步积累了图形变换的数学活动经验。

八年级学生思维从经验型逐步走向理论型，观察能力、记忆力、想象力迅速发展。

有强烈的独立思考，自主探究的愿望。

教学目标：
1、知识与技能目标：复习掌握旋转的定义及性质。

2、过程与方法目标：通过对图形观察，操作，探究，增强分析解决问题的能力。

3、情感与态度目标：发展学生的数学观。

教学重点：图形旋转的性质。

教学难点：明确旋转的研究对象。

教法：通过层层递进的问题引发学生的思考，启发引导式。

学法：通过操作感悟，通过交流明晰。

教学过程：。

第三章图形的平移与旋转3.3 中心对称一、教材分析本章位于北师大版八年级下第三章，是继小学已经学过了平移和旋转基础之上进行深入学习。

具有呈上启下的作用。

本章先通过观察具体的平移、旋转现象，分析、归纳并概括出平移、旋转的整体规律和基本性质，然后再平移和旋转的设计、欣赏、简单应用中，进一步深化对图形三种基本变化的理解和认识。

也对后面学习平行四边形等特殊的四边形起了铺垫的作用。

本节内容是继《图形旋转》后的一节内容，在本章中起了非常重要的作用，前面的几节内容研究一般图形的旋转，本节是研究两个图形通过特殊的旋转而产生的特殊位置关系，体现了从一般到特殊的思想。

而研究这种特殊的位置关系为我们几何图形的分析提供了更多的手段，比如平行四边、正偶数边形正是二、学情分析学生的知识技能基础：在七年级（下）和本章前面几节课中，已学习了轴对称、平移、旋转等概念，学生已充分理解了各种变换的基本性质，具备了分析、设计图案的基本技能。

学生活动经验基础：在相关知识的学习过程中，学生已经初步积累了一定的图形变换的数学活动经验，本节课旨在让学生在进行观察、分析、欣赏等操作性活动中，丰富学生对图形变换的认识，并使他们正确理解和把握平移、旋转等内容，进一步深化对图形的三种基本变换的理解和认识。

三、教学目标（一）知识与技能：1.了解中心对称、中心对称图形的概念，探索它的基本性质；2.会进行简单的中心对称作图；3.认识并欣赏现实生活中的中心对称；（二）过程与方法：经历有关中心对称的观察、操作、欣赏、归纳、验证、设计的过程，进一步积累数学活动经验，增强学生的动手实践能力，发展空间观念。

（三）情感、态度与价值观：通过图形间的变化关系，使学生认识到一切事物的变化可以通过一系列的基本变化组合得到，体会事物从量变到质变的过程。

四、教学重点中心对称、中心对称图形的概念；作出一个图形关于一点的对称图形；五、教学难点两个图形成中心对称与中心对称图形的区别和联系；六、重难点突破：问题串设置逐层推进，达到目标核心。

第三章图形的平移与旋转3.1 ．图形的平移（一）教课目的：经过详细实例认识平移，理解平移的基本内涵，理解平移前后两个图形对应点连线平行且相等、对应线段和对应角分别相等的性质。

教课过程：第一环节：创建情境活动内容：1.引入问题，出现课题：赏识生活中，我们常常有到的一些漂亮的图案和汽车标记以及漂亮的花边！感觉生活中的平移的经验！引入新的问题！请你判断：小明随着妈妈乘参观电梯上楼，一会儿，小明喜悦地大喊起来：“妈妈！妈妈！你看我长高了！我比对面的大楼还要高！”小明说的对吗？为何？2.接触平移现象：教师经过多媒体展现（展现画面）现实生活中平移的详细实例：（1）箱子在传递带上挪动的过程。

（2）手扶电梯上人的挪动的过程。

教师发问：① 你能发现传递带上的箱子、手扶电梯上的人在平移前后什么没有改变，什么发生了改变吗？②在传递带上，假如箱子的某一按键向前挪动了 80cm，那么电视机的其余部位（如屏幕左上角的图标）向什么方向挪动？挪动了多少距离？③假如把挪动前后的同一箱子当作长方体（多媒体演示书上的图 3-2 ），那么四边形与四边形的形状、大小能否同样？学生自由讲话，畅所欲言。

平移前后两个图形的形状和大小没有改变，地点发生了改变。

第二环节：活动研究活动一：研究平移的定义内容：依据上述剖析，你能说明什么样的图形运动称为平移？教师指引学生从语句的主谓剖析来对待以上几个句子，让学生自己总结平移的观点：（主语――状语――谓语）“一个物体沿着某个方向挪动必定的距离”在学生发现和概括的基础上板书：平移定义：在平面内，将一个图形沿某个方向挪动必定的距离，这样的图形运动称为平移。

平移不改变图形的形状和大小。

注意：平移三因素：几何图形——运动方向——运动距离活动二：研究平移的性质学生联合 P65 图 3-1 的内容和 P66图 3-2 的内容自主学习学生概括总结，教师板书平移的性质：经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等。

第三章图形的平移与旋转第1节图形的平移教学目标1、通过具体实例认识平面图形的移，探索它的基本性质，会进行简单的平移画图。

2、在直角坐标系中，能写出一个已知顶点坐标的多边形沿坐标轴方向平移后图形的顶点坐标，并知道对应顶点坐标之间的关系。

3、在直角坐标系中，探索并了解将一个多边形依次沿两个坐标轴平移后所得到的图形与原来的图形具有平移关系，体会图形顶点坐标的变化。

4、认识的欣赏平移在自然界和现实生活中的应用。

5、经历有关平移的观察、操作、分析及抽象、概括等过程，进一步积累数学活动经验，增强动手实践能力，发展空间观念。

教学重点平移的性质，利用平移性质作图，在平面直角坐标系里进行平移操作。

教学难点平移作图，坐标的变化与平移规律之间的关系。

教学过程：3个课时第一课时图形的平移一、导入新课生活中的平移：P65“传送带上的电视机的形状、大小是否发生了改变”、“手扶电梯上的人”、“笔直的铁道上行驶的火车”、“上下楼的电梯”二、平移1、定义：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

2、如图：P65，对应点、对应线段、对应角三、做一做：P65四、平移的性质一个图形和它经过平移所得的图形中，对应点所连的线段平行（或在一条直线上）且相等；对应线段平行（或在一条直线上）且相等，对应角相等。

五、例：P66六、想一想：P67在上面例中，你还有画△DEF的其他方法吗？七、议一议：P67确定一个图形平移后的位置，需要哪些条件？（要原先的图形、平移方向、平移距离）八、练习：P67，P67-68九、作业：1、把图中的机器人向右平移2格，再向下平移2格， 画出最后平移的图形。

2、如图，在长宽分别为20M 、10M 的长方形草地上有一条宽 为1M 的弯曲小路，求草地的面积。

3、已知正方形边长为10米，从A 点爬到B 点沿折线走路程是多少？第二课时 在坐标系里上、下、左、右平移与坐标的关系一、回顾图形平移的性质二、思考：P68三、想一想：P69A B四、议一议：P69五、平移小结1、纵坐标不变，横坐标分别增加（减少）a 个单位时，图形 平移a 个单位；2、横坐标不变，纵坐标分别增加（减少）a 个单位时，图形 平移a 个单位。

第三章图形的平移与旋转1 图形的平移第1课时平移教师备课素材示例●归纳导入观察下列图片，你能发现图中描绘的运动的共同点吗？这种现象是实际生活中的平移现象，今天我们来学习平移的相关知识．【归纳】在平面内，将一个图形沿着某一个方向移动一定的距离，这样的图形运动称为平移．平移前后两个图形的形状和大小没有改变，位置发生了改变．【教学与建议】教学：通过生活实例使学生初步感受到生活中的平移现象，渗透平移的三要素，归纳平移定义．建议：让学生各抒己见，用自己所学的知识合情推理并得出自己的结论．●置疑导入活动内容：我们大家共同来看小亮同学的一天．1．小亮早晨起来，推开卧室门，刷牙洗漱准备上学；2．小亮乘坐电梯，到达楼下；3．小亮骑上自行车到学校去；4．小亮路过公园看到有小朋友在玩滑梯．问题1：请大家思考并分组讨论一下，以上几种运动现象有什么共同点？问题2：根据上述分析，你能说明什么样的图形运动被称为平移吗？问题3：平移运动中，对于运动主体(图形)，在形状、位置、大小这三个因素中，哪些因素发生了变化，哪些保持不变？问题4：展示图片，指出哪些运动是平移．问题5：下列现象中，属于平移的有(1)(3)(5).(1)火车在笔直的铁轨上行驶；(2)冷水受热过程中小气泡上升变成大气泡；(3)打气筒打气时，活塞的运动；(4)钟摆的摆动；(5)传送带运送物品．【教学与建议】教学：设置问题，培养学生的学习兴趣和归纳概括能力．建议：问题1，2，3.由学生分小组讨论完成，问题4和问题5让学生在学会的基础上进行练习，巩固对平移概念的理解．解此类题目的关键是判断在图形平移前后，图形形状和大小是否改变，平移改变的只有位置．【例1】下列图案中，可以由第一个图案平移得到的是(C)经过平移，对应点所连的线段平行(或在一条直线上)且相等；对应线段平行(或在一条直线上)且相等，对应角相等．【例2】如图，将△ABC沿BC方向平移1cm得到△DEF，若△ABC的周长为14cm，则四边形ABFD的周长为(A)A．16cmB．18cmC．20cmD．22cm（例2题图）（例3题图）【例3】如图，△OAB的顶点B的坐标为(4，0)，把△OAB沿x轴向右平移得到△CDE，如果CB＝1，那么OE的长为__7__．确定图形平移方式的关键是确定出图形平移前后的对应点，再确定图形中的关键点，作出关键点的对应点．【例4】如图，在6×6的方格中有两个涂有阴影的图形M，N，图①中的图形M平移后位置如图②所示，以下对图形M的平移方法叙述正确的是(C)A．向右平移2个单位长度，向下平移3个单位长度B．向右平移1个单位长度，向下平移3个单位长度C．向右平移1个单位长度，向下平移4个单位长度D．向右平移2个单位长度，向下平移4个单位长度【例5】如图，作出图形经过平移后的图形，使点A与点A′对应．一个图形平移前后面积周长相等．解题时，要抓住平移的距离，注意观察平移前后图形的关系，从而求解．【例6】如图，将面积为4的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，那么图中的四边形ACED的面积为__12__．（例6题图）（例7题图）【例7】如图，长方形ABCD的长为6，宽为4.将长方形先向上平移2个单位长度，再向右平移2个单位长度得到长方形A′B′C′D′，则阴影部分的面积是__8__．高效课堂教学设计1．通过具体实例认识平移，理解平移的基本内涵，掌握平移的基本性质．2．会画简单的平移图形．▲重点探索图形平移的主要特征和基本性质，会画简单图形的平移图．▲难点探索和理解平移的基本性质及性质的应用．◆活动1 创设情境导入新课(课件)请同学们观察下面的两幅图片：问题1：你能发现传送带上的箱子和手扶电梯上的人在移动前后什么没有改变，什么发生了改变吗？问题2：在传送带上，如果箱子的把手向前移动了80cm，那么箱子的其他部位向什么方向移动？移动的距离是多少？问题3：如果把移动前后的同一个箱子看成长方体，那么移动前后的长方体各个面的形状、大小是否相同？讨论得出：平移前后两个图形的形状和大小没有改变，位置发生了改变．这节课我们继续学习平移的一些知识．◆活动2 实践探究交流新知【探究1】平移的定义问题 1.根据上述分析，你能说明什么样的图形运动被称为平移吗？如何定义平移呢？问题2.根据平移的定义，你认为平移应具备哪几个要素？【归纳】1.平移的定义：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移．平移不改变图形的形状和大小．2．平移三要素：(1)几何图形；(2)运动方向；(3)运动距离．【探究2】探究平移的性质如图所示，△ABE沿射线XY的方向平移一定距离得到△CDF.点A，B，E分别平移到了点__C__，__D__，__F__；线段AB，BE，AE分别平移到了__CD__，__DF__，__CF__；∠ABE，∠BAE，∠AEB分别平移到了__∠CDF__，__∠DCF__，__∠CFD__．做一做：如图，四边形ABCD沿某方向平移后得到四边形EFGH，思考：(1)四边形ABCD是沿什么方向平移后得到四边形EFGH的，平移的距离是多少？(2)在图中，线段AE，BF，CG，DH有怎样的位置关系？(3)每对对应线段之间有怎样的位置关系？(4)图中有哪些相等的线段、相等的角？讨论分析：(1)变换前后对应点的连线平行且相等：平移变换是图形的每一个点的变换，一个图形沿某个方向移动一定的距离，那么每一个点也沿着这个方向移动相同的距离，所以对应点的连线平行且相等．(2)变换前后的图形全等：平移变换是由一个图形沿着某个方向移动一定的距离，所以平移前后的图形是全等的．(3)变换前后对应角相等．(4)变换前后对应线段平行且相等．【归纳】平移的性质：一个图形和它经过平移所得的图形中，对应点所连的线段平行(或在一条直线上)且相等，对应线段平行(或在一条直线上)且相等，对应角相等．◆活动3 开放训练应用举例【例1】下列图形中，哪一个可以通过平移得到( )A B C D【方法指导】注意仔细观察，一要判别大小是否变化；二要判别图形是否沿着一定的方向移动了一定的距离．由上可知，只有D项符合平移的概念．答案：D【例2】如图①，在宽20m，长32m的长方形地面上修同样宽的不规则的路(路始终垂直或平行于长方形地面的边)，余下的部分作为耕地，耕地面积为540m2，设路宽为xm，根据题意可列方程为______________．图①图②【方法指导】利用平移把不规则的路平移成规则的路，使耕地成为一个规则的长方形(如图②)，利用长方形的面积公式可列出方程．由于道路宽为xm，则耕地的长为(32－，所以根据题意可得方程：(32－x)(20－x)＝540.答案：(32－x)(20－x)＝540【例3】如图，经过平移，△ABC的顶点A移到了点D.画出平移后的三角形．【方法指导】确定一个图形平移后的位置，需要几何图形、运动方向、运动距离三要素，利用平移的定义和性质，找到关键点，用虚线画辅助线，实线画平移前后的图形．解：如图．画法一：过点D分别作出与AB，AC平行且相等的线段DE，DF，连接EF，△DEF就是△ABC平移后的图形．画法二：因为平移后的图形与原图形全等，所以过点B作线段BE，使它与线段AD平行且相等，得到另一个对应点E，用同样的方法得到点C 的对应点F，连接DE，EF，F D.△DEF就是△ABC平移后的图形．◆活动4 随堂练习1．下列说法中正确的是(D)A．一个图形经过平移后，与原图形成轴对称B．如果两个图形成轴对称，那么一个图形可由另一个图形经过平移变换得到C．一个图形经过平移后，它的性质发生了变化D．图形的平移由平移的方向和距离决定2．若△ABC沿东南方向平移了4cm，那么△ABC中BC上的中点D向__东南__方向移动了__4__cm.3．如图，∠DEF是由∠ABC经过平移得到的．若∠ABC＝33°，则∠DEF 的度数是__33°__．（第3题图）（第4题图）4．如图，大长方形的长是12cm，宽是10cm，阴影部分的宽均为2cm，则空白部分的面积是__80_cm2__.5．课本P67随堂练习◆活动5 课堂小结与作业【学生活动】1．这节课你有什么收获？2．我们在探索图形的平移时，运用了哪些方法？【教学说明】梳理本节课的重要方法和知识，加深对图形平移的特征、基本性质、作图等知识的理解和运用．【作业】课本P67习题3.1中的T1、T2、T3、T5.对于本节课，学生对“一个图形和它经过平移所得的图形中，对应点所连的线段平行(或在一条直线上)且相等；对应线段平行(或在一条直线上)且相等，对应角相等”这一结论得出比较顺利．教师应对小组讨论给予适当的指导，包括知识的启发引导、学生交流合作中注意的问题等，使小组合作学习更具实效性，给学生充分的思考时间，让学生发表见解，讨论看法，达到学以致用的目的．。

北师大版初二数学下册第三章图形的平移与旋转3教学目标：【知识与技能】1．了解中心对称、中心对称图形的概念，探究它的差不多性质；2．能综合运用变换解决有关问题。

【过程与方法】通过观看、操作，观赏等过程，使学生更深刻地明白得轴对称、旋转及组合等几何变换的规律和特点，并体会图形之间的变换关系，增强动手能力，进展空间观念。

【情感态度】运用讨论交流等方式，让学生自己探究出图形变化的过程，进展学生的图形分析能力、化归意识，感受中心对称的旋转之美。

【教学重点】正确明白得中心对称图形的定义和性质，中心对称图形及中心对称的区别与联系。

【教学难点】判定一个图形是否为中心对称图形，中心对称图形与成中心对称的区别与联系。

学生分析：本节课教学对象是八年级学生，思维活跃，爱好广泛，善于摸索，对多媒体（电子白板）教学环境比较熟悉，但学习层次不够整齐，抽象思维并不是专门强，他们明白得旋转变化是比较困难的，因此在教学过程中通过观赏动画，动手操作，让学生自主探究，分组讨论，引导他们由浅入深，步步推进，从广度，高度，深度上开拓学生思维，进行教学设计时，力争从教学内容，教学形式中表达趣味性，贴近生活，激发学生的好奇心。

教学方法设计：中心对称图形的旋转是学生学习的难点，为让学生对此有个感性认识，教学时利用电子白板的演示一些动画，把动态的问题直观的表现出来，让学生通过观看、摸索、小组合作交流，发觉中心对称图形的定义和性质。

其中，小组合作形式为要紧教学组织形式，通过小组合作学习，培养学生团结合作的能力。

教学媒体：电子白板教学过程：一.创设情境展现"生活中的对称之美"(轴对称图案),以上图片差不多上我们学过的什么对称图形?二.引入新课轴对称图形让我们感受到了对称之美，是因为轴对称图形具有什么特点呢？（沿着某条直线折叠后，两旁部分能够完全重合。

）接下来让我们一起来观赏一组车标图案,这些图案美吗？它们是轴对称图形吗？我们来看看这些图形有什么共同特点。

【精选】北师版八年级下册数学第三章《图形的平移与旋转》优秀教案1 图形的平移第1课时图形平移的概念与性质【教学目标】1。

经历探索图形平移基本性质的过程以及与他人合作交流的过程，进一步发展空间观念，增强审美意识。

2。

通过具体实例认识平移，理解平移的基本概念，理解平移前后两个图形对应点连线平行且相等、对应线段和对应角分别相等的性质。

【重难点】重点探索图形平移的主要特征和基本性质。

难点探索平移的基本性质及性质的应用。

【教学设计】一、情境导入教师通过多媒体展示(展示画面)现实生活中平移的具体实例：(1)箱子在传送带上移动的过程。

(2)手扶电梯上人的移动的过程。

学生观察多媒体展示的图片，教师提问：①你能发现传送带上的箱子、手扶电梯上的人在平移前后什么没有改变，什么发生了改变吗？②在传送带上，若箱子的某一按键向前移动了 80 cm，那么箱子的其他部位向什么方向移动？移动了多少距离？③如果把移动前后的同一箱子看成长方体，那么它的形状、大小是否相同？引导学生得出：平移前后两个图形的形状和大小没有改变，位置发生了改变。

二、探究新知1。

平移的定义师：根据上述分析，你能说明什么样的图形运动称为平移？在学生发现和归纳的基础上板书：平移的概念：在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为平移。

平移不改变图形的形状和大小。

平移三要素：几何图形，运动方向，运动距离。

2。

探究平移的性质(1)课件出示：如图，△ABC 经过平移得到△DEF，点A，B，C分别平移到了点D, E，F.点A与点D是一组对应点，线段AB与线段DE是一组对应线段，∠BAC与∠EDF是一组对应角。

①线段AD，CF，BE有怎样的位置关系？②图中每对对应线段之间有怎样的位置关系？③图中有哪些相等的线段、相等的角？处理方式：学生分成四人一组，共同探讨平移的性质。

学生归纳总结：经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等。

第三章图形的平移与旋转1。

通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中，对应点所连的线段平行(或在一条直线上)且相等；对应线段平行（或在一条直线上)且相等，对应角相等。

2。

认识并欣赏平移在自然界和现实生活中的应用.3.在直角坐标系中，能写出一个已知顶点坐标的多边形沿坐标轴方向平移后图形的顶点坐标,并知道对应顶点坐标之间的关系。

4。

在直角坐标系中,探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形与原来的图形具有平移关系，体会图形顶点坐标的变化.5.通过具体实例认识平面图形关于旋转中心的旋转,探索它的基本性质：一个图形和它经过旋转所得的图形中，对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角；对应线段相等,对应角相等.6。

了解中心对称、中心对称图形的概念,探索它的基本性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.7.认识并欣赏自然界和现实生活中的中心对称图形.8。

运用图形的平移、旋转、轴对称进行图案设计。

1。

经历有关平移与旋转的观察、操作、欣赏和设计的过程,进一步积累数学活动经验,增强动手实践能力,发展空间观念.2。

经历借助图形思考问题的过程，初步建立几何直观.3。

通过具体实例认识平移与旋转，探索它们的基本性质,会进行简单的平移、旋转画图。

4.在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移后图形的顶点坐标,并知道对应顶点坐标之间的关系.5.在直角坐标系中，探索并了解将一个多边形依次沿两个坐标轴方向平移后所得到的图形与原来的图形具有平移关系，体会图形顶点坐标的变化.6.了解中心对称、中心对称图形的概念，探索它的基本性质。

1。

在研究平移与旋转的过程中,进一步发展空间观念.2.认识并欣赏平移、旋转在自然界和现实生活中的应用,认识并欣赏自然界和现实生活中的中心对称图形.在前面的学习中学生已对诸如翻折、平移、旋转、轴对称等知识有了一定的认识与理解，只是平移和旋转的知识没有正式出现罢了，但这些变换的意识学生已经有了.学生学习了本章知识后对平移与旋转以及轴对称这三种常用的全等变换有了系统的认识,但学生把握这些全等变换的能力有待提升,特别是对组合图案的形成过程的分析是学生把握不好的地方，应加强训练。