截面轴心受压构件的稳定系数怎么查
- 格式:doc
- 大小:126.82 KB
- 文档页数:1

钢结构强度稳定性计算书计算依据:1、《钢结构设计规范》GB50017-2003一、构件受力类别:轴心受压构件。
二、强度验算:1、轴心受压构件的强度,可按下式计算:σ = N/A n≤ f式中N──轴心压力,取N= 10 kN;A n──净截面面积,取A n= 298 mm2;轴心受压构件的强度σ= N / A n = 10×103 / 298 = 33.557 N/mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;由于轴心受压构件强度σ= 33.557 N/mm2≤承载力设计值f=205 N/mm2,故满足要求!2、摩擦型高强螺栓连接处的强度,按下面两式计算,取最大值:σ = (1-0.5n1/n)N/A n≤ f式中N──轴心压力,取N= 10 kN;A n──净截面面积,取A n= 298 mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;n──在节点或拼接处,构件一端连接的高强螺栓数目,取n = 4;n1──所计算截面(最外列螺栓处)上高强螺栓数目;取n1 = 2;σ= (1-0.5×n1/n)×N/A n=(1-0.5×2/4)×10×103/298=25.168 N/mm2;σ = N/A ≤ f式中N──轴心压力,取N= 10 kN;A──构件的毛截面面积,取A= 354 mm2;σ=N/A=10×103/354=28.249 N/mm2;由于计算的最大强度σmax = 28.249 N/mm2≤承载力设计值=205 N/mm2,故满足要求!3、轴心受压构件的稳定性按下式计算:N/φA n≤ f式中N──轴心压力,取N= 10 kN;l──构件的计算长度,取l=5000 mm;i──构件的回转半径,取i=23.4 mm;λ──构件的长细比, λ= l/i= 5000/23.4 = 213.675;[λ]──构件的允许长细比,取[λ]=250 ;构件的长细比λ= 213.675 ≤[λ] = 250,满足要求;φ──轴心受压构件的稳定系数, λ=l/i计算得到的构件柔度系数作为参数查表得φ=0.165;A n──净截面面积,取A n= 298 mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;N/(φA n)=10×103/(0.165×298)=203.376 N/mm2;由于σ= 203.376 N/mm2≤承载力设计值f=205 N/mm2,故满足要求!。

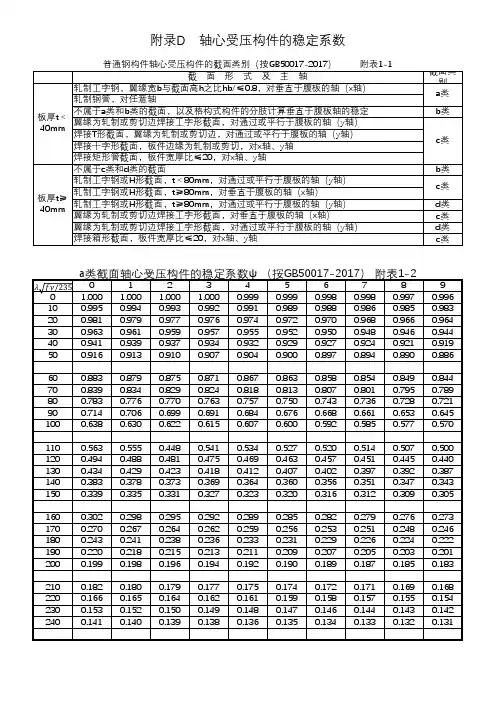
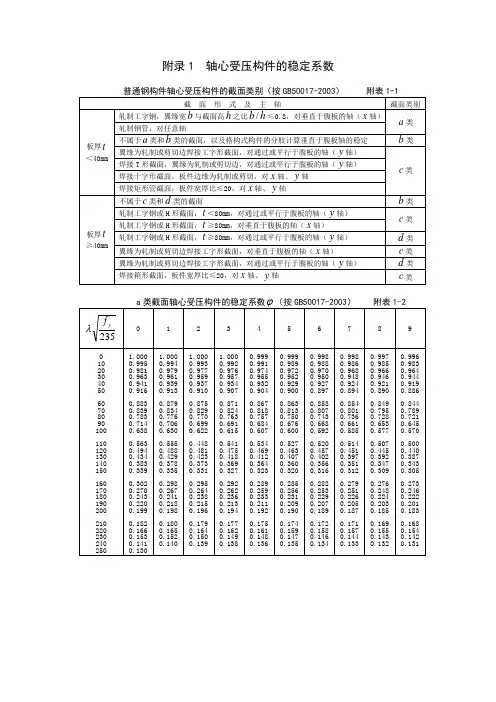
附录B 轴心受压构件的稳定系数B.0.1 轴心受压构件的稳定系数ϕ应按下式计算:2212ηλϕλ++= (B.0.1-1) 式中 η —— 构件的几何缺陷系数,应按下式计算:()0λλαη-= (B.0.1-2) 对于T6类合金:0.22α=,00.15λ=;对于非T6类合金:0.35α=,00.05λ=。
λ —— 相对长细比,应按下式计算:λ= (B.0.1-3) e A —— 有效毛截面面积(mm 2);cr N —— 基于毛截面的欧拉临界力(N ),应按下式计算: 2cr 20x xEI N l π= (B.0.1-4)0x l —— 构件对截面主轴的计算长度(mm ); x I —— 构件毛截面对其主轴的惯性矩(mm 4)。
B.0.2 对于存在局部焊接的轴心受压构件,其局部焊接稳定系数haz ϕ应按下式计算:2haz haz 2haz 12ηλϕλ++= (B.0.2-1) 式中 haz λ —— 局部焊接相对长细比,应按下式计算:haz λ= (B.0.2-2)u,e A —— 有效焊接截面面积(mm 2);cr N —— 基于毛截面的欧拉临界力(N ); u f —— 铝合金材料的极限抗拉强度最小值(N/mm 2)。
B.0.3 单轴对称截面的轴心受压构件,对非对称轴的相对长细比x λ仍应按式(B.0.1-3)计算(或局部焊接下,haz x λ按式(B.0.2-2)),但对对称轴应取计及扭转效应的下列换算相对长细比y ωλ代替y λ(或局部焊接下y λ代替,haz y λ): yωλ= ,haz y ωλ= (B.0.3-1)式中 y N ω—— 基于毛截面的单轴对称截面弯扭屈曲临界力(N ),应按下式计算:0021y y N y ω-⎣⎦ (B.0.3-2)y N —— 基于毛截面的对y 轴的欧拉临界力(N ),应按下式计算: 2y 2y EA N πλ= (B.0.3-3)y λ —— 构件绕对称轴的长细比;N ω—— 基于毛截面的扭转屈曲临界力(N ),应按下式计算: 2t 2201EI N GI i l ωωωπ⎛⎫=+ ⎪⎝⎭(B.0.3-4)I ω —— 毛截面扇性惯性矩(mm 4); t I —— 毛截面抗扭惯性矩(mm 4); l ω —— 扭转屈曲计算长度(mm ),应按附表C 中表C-1的规定进行计算;G —— 铝合金材料的剪切模量(N/mm 2),应按下式计算: 2(1)E G ν=+ (B.0.3-5)E —— 弹性模量;ν—— 泊松比;0i —— 截面对剪心的极回转半径(mm ),应按下式计算:0i = (B.0.3-6)x y i i , —— 构件毛截面对其主轴x 轴和y 轴的回转半径(mm ); 00x y , —— 截面剪心坐标(mm )。

钢筋混凝土轴心受压构件的稳定系数表1. 引言钢筋混凝土结构是现代建筑中常见的一种结构形式,其具有较好的承载能力和耐久性。
在钢筋混凝土结构中,轴心受压构件承担着重要的承载任务。
为了确保轴心受压构件在使用过程中的安全性和稳定性,需要对其进行充分的设计和计算。
本文将介绍钢筋混凝土轴心受压构件的稳定系数表。
2. 稳定系数的概念及意义在钢筋混凝土结构设计中,稳定系数是评估结构稳定性和安全性的重要指标之一。
稳定系数反映了结构在受力作用下抵抗失稳破坏的能力。
对于轴心受压构件来说,其失稳破坏形式主要有屈曲、侧扭和局部失稳等。
通过计算得到轴心受压构件的稳定系数表,可以直观地了解不同参数对于结构稳定性的影响,为工程师提供设计参考和决策依据。
稳定系数表中的数据是基于理论计算和试验结果得出的,对于结构设计和施工具有重要的指导意义。
3. 稳定系数表的内容和格式钢筋混凝土轴心受压构件的稳定系数表通常包括以下内容:3.1 构件几何参数稳定系数表中需要包含轴心受压构件的几何参数,如截面形状、尺寸、钢筋布置等。
这些参数对于结构的承载能力和稳定性有重要影响。
3.2 材料参数稳定系数表中需要包含轴心受压构件所使用材料的参数,如混凝土抗压强度、钢筋强度等。
这些参数是计算稳定系数的基础。
3.3 稳定系数计算方法稳定系数表中需要说明计算稳定系数所使用的方法和公式。
常见的计算方法包括欧拉公式、约束条件法等。
不同方法适用于不同类型的结构,工程师可以根据实际情况选择合适的方法进行计算。
3.4 稳定系数示例计算为了方便工程师使用稳定系数表,表中应包含一些示例计算。
这些示例计算可以覆盖不同类型的轴心受压构件,展示不同参数对于稳定系数的影响。
3.5 结果解读和应用建议稳定系数表中需要对计算结果进行解读和分析,并给出相应的应用建议。
例如,当稳定系数小于某个阈值时,需要采取相应的加固措施来提高结构的稳定性。
4. 稳定系数表的编制和更新为了保证稳定系数表的准确性和可靠性,其编制需要遵循一定的原则和流程。




轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算,设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。
一、轴心受力构件的强度和刚度1.轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值;n A ——构件的净截面面积;f ——钢材的抗拉强度设计值。
采用高强度螺栓摩擦型连接的构件,验算最外列螺栓处危险截面的强度时,按下式计算:f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数;1n ——计算截面(最外列螺栓处)上的高强度螺栓数;0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆,除按式(2)验算净截面强度外,还应按下式验算毛截面强度f A N ≤=σ (4)2.轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比;[λ]——构件的容许长细比。
二、 轴心受压构件的整体稳定1.理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定:①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。
②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。
③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。
2.理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形,临界力公式即为著名的欧拉临界力公式,表达式为N E =22l EI π=22λπEA (6) 3.初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷,这些缺陷会降低轴心受压构件的稳定承载力。
1)残余应力的影响当轴心受压构件截面的平均应力p f >σ时,杆件截面内将出现部分塑性区和部分弹性区。
由于截面塑性区应力不可能再增加,能够产生抵抗力矩的只是截面的弹性区,此时的临界力和临界应力应为:N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩);I ——全截面的惯性矩。

钢筋混凝土轴心受压构件的稳定系数是一个重要的参数,用于评估构件在受压状态下的稳定性。
在钢筋混凝土结构设计中,轴心受压构件承受的压力会引起构件的变形和破坏,因此需要通过稳定系数来考虑构件的稳定性,确保结构的安全性和可靠性。
在本文中,我将深入探讨钢筋混凝土轴心受压构件的稳定系数表,并分享一些关于这个主题的观点和理解。
1. 稳定系数的定义和意义稳定系数是指构件在受压状态下的稳定性与材料强度之间的比值。
它的值代表了构件抵抗稳定性失效的能力,是判断结构是否满足稳定性要求的关键指标。
稳定系数的计算通常基于一定的假设和理论模型,考虑到材料的弹性模量、几何形状、截面特性以及加载方式等因素。
通过建立稳定系数表,我们可以根据构件的几何形状和受力情况,查找相应的稳定系数值,从而进行结构设计和评估。
2. 稳定系数表的结构和内容稳定系数表包括了各种不同构件和截面形状的稳定系数数值,供工程师和设计人员参考使用。
它通常按照构件的类型和截面形状进行分类,提供了一系列的稳定系数数值。
稳定系数表的结构可以按照以下方式进行组织:2.1 构件类型分类:比如梁、柱、墙等,每种构件类型都有独立的稳定系数表。
2.2 截面形状分类:对于每种构件类型,按照不同的截面形状建立子表,比如矩形截面、圆形截面、T形截面等。
2.3 参数分类:在每个子表中,根据构件的尺寸、材料强度和约束条件等参数,列出相应的稳定系数数值。
3. 稳定系数表的应用和设计原则稳定系数表是钢筋混凝土结构设计中的重要工具,为设计人员提供了参考数值,帮助他们评估和选择合适的构件尺寸和截面形状。
在使用稳定系数表时,设计人员应该遵循以下几个原则:3.1 参考适用范围:稳定系数表通常针对一定的材料强度、构件尺寸范围和约束条件进行编制,设计人员需要根据实际情况选择合适的表格进行参考。
3.2 综合考虑各因素:稳定系数的数值取决于材料的强度、构件的几何形状和加载方式等因素,设计人员需要对这些因素进行综合考虑,以确保稳定系数的准确性和适用性。