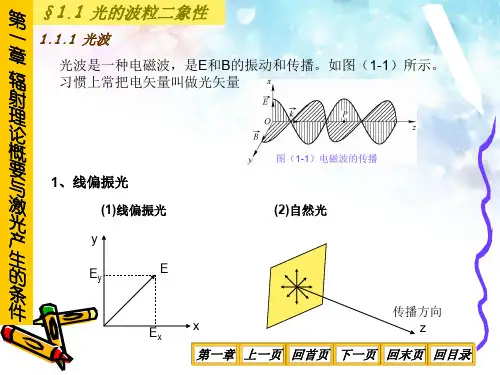
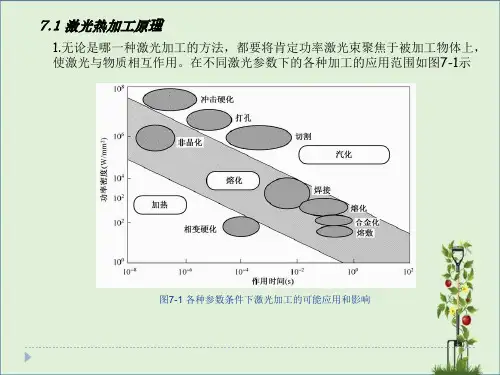
new激光原理及应用 第二版 (陈家壁 著)

陈家璧版光学信息技术原理及应用习题解答(7-8章)-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII第七章 习题解答1. 某种光盘的记录范围为内径80mm,外径180mm 的环形区域,记录轨道的间距为2um.假设各轨道记录位的线密度均相同记录微斑的尺寸为um,试估算其单面记录容量. (注: 内、外径均指直径)解： 记录轨道数为 25000002.0280180=⨯-=N单面记录容量按位计算为 ∑=⨯≈⨯+=Nn n M 110107.10006.0)002.040(2π bits = 17 Gb.按字节数计算的存储容量为 2.1GB.2. 证明布拉格条件式（7-1）等效于（7-17）式中位相失配= 0的情形， 因而（7-18）式描述了体光栅读出不满足布拉格条件时的位相失配。

证明: 将体光栅读出满足布拉格条件时的照明光波长(介质内) 和入射角 (照明光束与峰值条纹面间夹角)分别记为0和θ0, 则根据布拉格条件式（7-1）有: 2sin θ0= 0 其中为峰值条纹面间距.对于任意波长λa (空气中) 和入射角θr (介质内), 由(7-17)式, 位相失配 δ 定义为:24)cos(n K K ar πλθφδ--=其中n 0为介质的平均折射率, K = 2π/Λ为光栅矢量K 的大小，φ为光栅矢量倾斜角，其值为 22πθθφ++=sr ，θr 为再现光束与系统光轴夹角 (参见图7-9)．当 δ = 0 时,有2422cos n K K a r s r πλθπθθ=⎪⎭⎫ ⎝⎛-++ 即:Λ=Λ=⎪⎭⎫ ⎝⎛-2422sin 0λππλθθn s rλ为介质中的波长. 由于角度2sr θθ-恰为照明光与峰值条纹面的夹角θ, ∑ ©亦即布拉格条件2Λ sin θ = λ.当读出光偏离布拉格角θo 和布拉格波长λo 的偏移量分别为∆θ和∆λ时，有[]0200200002044sin )sin(cos )cos( 4)()(cos n K n K K K n K K πλπλθθφθθφπλλθθφδ∆--∆--∆-=∆+-∆+-=利用布拉格条件式(7-17), 以及∆θ和∆λ很小时的近似关系 cos ∆θ≈1 和 sin ∆θ≈∆θ, 立即可得:δ =∆θK sin(φ-θ0) - ∆λK 2/4πn 0 即(7-18)式 原题得证。

思考练习题11． 试计算连续功率均为1W 的两光源，分别发射λ＝0.5000μm ，ν=3000MHz 的光，每秒从上能级跃迁到下能级的粒子数各为多少？答：粒子数分别为：188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2．热平衡时，原子能级E 2的数密度为n 2，下能级E 1的数密度为n 1，设21g g =，求：(1)当原子跃迁时相应频率为ν＝3000MHz ，T ＝300K 时n 2/n 1为若干。

(2)若原子跃迁时发光波长λ＝1μ，n 2/n 1＝0.1时，则温度T 为多高？答：（1）(//m n E E m m kTn n n g e n g --=）则有：1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν（2）K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3．已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0－18J ，设火焰(T ＝2700K)中含有1020个氢原子。

设原子按玻尔兹曼分布，且4g 1＝g 2。

求：(1)能级E 2上的原子数n 2为多少？(2)设火焰中每秒发射的光子数为l08 n 2，求光的功率为多少瓦？答：（1）1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n（2）功率＝W 918810084.51064.13110--⨯=⨯⨯⨯4．(1)普通光源发射λ＝0.6000μm 波长时，如受激辐射与自发辐射光功率体密度之比q q 激自1=2000，求此时单色能量密度νρ为若干？(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ，λ为0.6328μm ，设μ＝1，求q q 激自为若干？ 答：（1）3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ＝自激（2）943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q ＝自激5．在红宝石Q 调制激光器中，有可能将全部Cr 3＋(铬离子)激发到激光上能级并产生巨脉冲。

第一章 习题解答1.1 已知不变线性系统的输入为()()x x g comb = 系统的传递函数⎪⎭⎫⎝⎛bfΛ。

若b 取（1）50=.b （2）51=.b ，求系统的输出()x g '。

并画出输出函数及其频谱的图形。

答：（1）()(){}1==x x g δF 图形从略， （2）()()()()()x s co f f δf δx g x x x πδ232+1=⎭⎬⎫⎩⎨⎧1+31+1-31+=F 图形从略。

1.2若限带函数()y x,f 的傅里叶变换在长度L 为宽度W 的矩形之外恒为零， （1）如果L a 1<，Wb 1<，试证明()()y x f y x f b x a x ab ,,sinc sinc =*⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛1 证明：(){}(){}(){}()()(){}(){}()y x,f sinc sinc 1,,y x,f ∴,,,,y x,f ====bxa x ab bf af rect y x f bf af rect y x f Wf L f rect y x f y x yx yx F F F F F 1-（2）如果L a 1>， Wb 1>，还能得出以上结论吗？ 答：不能。

因为这时(){}(){}()y x yx bf af rect y x f Wf L f rect y x f ,,F ,,F ≠⎪⎪⎭⎫ ⎝⎛。

1.3 对一个空间不变线性系统，脉冲响应为 ()()()y x y x h δ77=sinc ,试用频域方法对下面每一个输入()y x f i ,，求其输出()y x g i ,。

（必要时，可取合理近似）（1）()x y x f π4=1cos ,答：()(){}(){}{}{}()(){}{}{}{}{}xcos x cos f rect x cos y 7x sin x cos y x h y x f y x g x πππδπ4=4=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛74=74==1-1-1-11-1F F F F F F F ,F ,F F ,（2）()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754=2y rect x rect x cos y x f π, 答：()(){}(){}{}()()(){}{}()()()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛77575⋅75*4=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754==1-1-11-2y rect x rect x cos f rect f sinc 75f sinc x cos y 7x sin y rect x rect x cos y x h y x f y x g x y x ππδπF F F F F ,F ,F F ,（3）()()[]⎪⎭⎫⎝⎛758+1=3x rect x cos y x f π,答：()()[]()(){}(){}()()()()()()()()()()()(){}⎪⎭⎫ ⎝⎛75=75≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛75*⎪⎭⎫ ⎝⎛4+81+4-81+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775*8+1=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛758+1=1-1-1-1-1-3x rect f 75f sinc f rect f 75f sinc f rect f δ75f sinc f f x f rect f δ75f sinc x cos y 7x sin x rect x cos y x g y x x y x x y x x x x y x δδδδδπδπF F F F F F F F ,（4）()()()()()y rect x rect x comby x f 22*=4, 答：()()()()(){}()(){}{}()()()()()()()()()()()()(){}()()x π6cos x π2cos f f f f f f f f f f f rect f f δf f δf f δf f δf rect f sinc 2f sinc f f com b y 7x sin y rect x rect x com by x g y x y x y x y x y x x yx y x y x y x x y x y x 1060-3180+250=3+0530-3-0530-1+1590+1-1590+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛-3-2120-1+6370+1-6370+41=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛7⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛2⎪⎭⎫ ⎝⎛41=722*=1-1-1-1-2...,.,.,.,.,F ,.,.,.,F F F F F ,δδδδ0.25δδδ1.4 给定一个不变线性系统，输入函数为有限延伸的三角波()()x x rect x comb x g i Λ*⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛50⎪⎭⎫ ⎝⎛331=对下述传递函数利用图解方法确定系统的输出。

第一章习题1.1 不变线性系统的输入为系统的传递函数。

假设b 取〔1〕50=.b 〔2〕51=.b ，求系统的输出()x g '。

并画出输出函数及其频谱的图形。

答：〔1〕()(){}1==x x g δF 图形从略，〔2〕()()()()()x s co f f δf δx g x x x πδ232+1=⎭⎬⎫⎩⎨⎧1+31+1-31+=F 图形从略。

()y x,f 的傅里叶变换在长度L 为宽度W 的矩形之外恒为零，（1）如果，，试证明证明：(){}(){}(){}()()(){}(){}()y x,f b x sinc a x sinc ab bf af rect y x f y x,f bf af rect y x f W f L f rect y x f y x,f y x y x y x *⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛1==∴=⎪⎪⎭⎫ ⎝⎛=,,F F ,,F ,,F F 1- （2）如果， ，还能得出以上结论吗？答：不能。

因为这时(){}(){}()y x y x bf af rect y x f W f L f rect y x f ,,F ,,F ≠⎪⎪⎭⎫ ⎝⎛。

1.3 对一个空间不变线性系统，脉冲响应为试用频域方法对下面每一个输入()y x f i ,，求其输出()y x g i ,。

〔必要时，可取合理近似〕〔1〕()x y x f π4=1cos ,答：()(){}(){}{}{}()(){}{}{}{}{}x cos x cos f rect x cos y 7x sin x cos y x h y x f y x g x πππδπ4=4=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛74=74==1-1-1-11-1F F F F F F F ,F ,F F ,〔2〕()()⎪⎭⎫ ⎝⎛75⎪⎭⎫⎝⎛754=2y rect x rect x cos y x f π, 答：()(){}(){}{}()()(){}{}()()()()⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛77575⋅75*4=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛75⎪⎭⎫ ⎝⎛754==1-1-11-2y rect x rect x cos f rect f sinc 75f sinc x cos y 7x sin y rect x rect x cos y x h y x f y x g x y x ππδπF F F F F ,F ,F F ,〔3〕()()[]⎪⎭⎫ ⎝⎛758+1=3x rect x cos y x f π, 答： ()()[]()(){}(){}()()()()()()()()()()()(){}⎪⎭⎫ ⎝⎛75=75≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775≅⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛7⎪⎭⎫ ⎝⎛75*⎪⎭⎫ ⎝⎛4+81+4-81+=⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛775*8+1=⎭⎬⎫⎩⎨⎧7⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛758+1=1-1-1-1-1-3x rect f 75f sinc f rect f 75f sinc f rect f δ75f sinc f f x f rect f δ75f sinc x cos y 7x sin x rect x cos y x g y x x y x x y x x x x y x δδδδδπδπF F F F F F F F , 〔4〕()()()()()y rect x rect x comb y x f 22*=4,答：1.4 给定一个不变线性系统，输入函数为有限延伸的三角波 对下述传递函数利用图解方法确定系统的输出。

贵州民族大学Gguizhou Minzu University 《激光原理及应用》课程论文论文题目：判向计数实验学院(系)：信息工程学院专业：光信息科学与技术年级： 2011 级姓名：汪灿学号： 201107040014完成时间： 2013年 12 月 9 日判向计数实验摘要：本文是对激光干涉测长系统组成设计，干涉条纹通过移相获得两路相位差为π/2的干涉条纹的光强信号，该信号经过放大、整形、倒相及微分等处理，可以获得四个相位依次相差π、2的脉冲信号。

判向计数电路将一个周期的干涉信号变成四个脉冲的输出信号，实现干涉条纹的四倍频.关键词：4倍频、整形、0P07一、激光干涉测长原理在激光干涉测长中，由于动镜在导轨上沿光轴移动，存在各种偶然因互的干扰（例如外界振动、导轨的平直度误差以及机械传动系统的不稳定等），使动镜产生偶然的反向运动，这种偶然的反向运动使计数器所显示的脉冲数为正反向移动的总数，而不是真正的被测长度，因此必然存在测长误差。

为了解决这一问题，经光电转换并放大整形后，信号进入一方向判别电路，该电路把计数脉冲分成加、减二种脉冲，工作台正向移动时引起的脉冲为加脉冲、反向移动时引起的脉冲为减脉冲、把这两种脉冲分开后送入可逆计数器计数。

方向判别电路的原理。

先在干涉系统中应用移相方法将干涉条纹分为两组且彼此位相偏移π/2，分别经光电转换后，输出的两组光电信号也彼此有π/2的位移偏移，这两组光电信号分别经放大、整形、倒相，变成四个位相依次差π/2的矩形脉冲，再经斯密特电路把波形变换成尖脉冲。

当工作台正向移动时，脉冲的排列为1、3、2、4 、1 ；反向移动时，脉冲排列次序为1 、 4、2、3、 1，如图1所示。

在逻辑电路上可根据脉冲1的后面是1或4来判别正向加脉冲或反向减脉冲，并分别逆入加脉冲的“门”或减脉冲的“门”中去，从而可得到总的加脉冲或减脉冲信号。

图1判向计数原理框图二、方案论证与设计1单片机模块选择方案一：采用89C51控制。

思考练习题11． 试计算连续功率均为1W 的两光源，分别发射λ＝0.5000μm ，ν=3000MHz 的光，每秒从上能级跃迁到下能级的粒子数各为多少？答：粒子数分别为：188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h qn 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2．热平衡时，原子能级E 2的数密度为n 2，下能级E 1的数密度为n 1，设21g g =，求：(1)当原子跃迁时相应频率为ν＝3000MHz ，T ＝300K 时n 2/n 1为若干。

(2)若原子跃迁时发光波长λ＝1μ，n 2/n 1＝0.1时，则温度T 为多高？答：（1）(//m n E E m m kT n n n g e n g --=）则有：1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kTh e n n ν（2）K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3．已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0－18J ，设火焰(T ＝2700K)中含有1020个氢原子。

设原子按玻尔兹曼分布，且4g 1＝g 2。

求：(1)能级E 2上的原子数n 2为多少？(2)设火焰中每秒发射的光子数为l08 n 2，求光的功率为多少瓦？答：（1）1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n（2）功率＝W 918810084.51064.13110--⨯=⨯⨯⨯4．(1)普通光源发射λ＝0.6000μm 波长时，如受激辐射与自发辐射光功率体密度之比q q 激自1=2000，求此时单色能量密度νρ为若干？(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ，λ为0.6328μm ，设μ＝1，求q q 激自为若干？ 答：（1）3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ＝自激（2）943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q ＝自激5．在红宝石Q 调制激光器中，有可能将全部Cr 3＋(铬离子)激发到激光上能级并产生巨脉冲。

《激光原理及应用》习题参考答案思考练习题11.解答：设每秒从上能级跃迁到下能级的粒子数为n 。

单个光子的能量：λνε/hc h == 连续功率：εn p =则，ε/p n =a. 对发射m μλ5000.0=的光： )(10514.2100.31063.6105000.01188346个⨯=⨯⨯⨯⨯⨯==--hc p n λ b. 对发射MHz 3000＝ν的光)(10028.51030001063.6123634个⨯=⨯⨯⨯==-νh p n 2.解答：νh E E =-12……………………………………………………………………..(a)TE E en nκ1212--=……………………………………………………………………….(b)λν/c =…………………………………………………………………………….(c) （1）由（a ），（b ）式可得：112==-T h e n n κν（2）由（a ），（b ）,(c)式可得： )(1026.6ln312K n n hcT ⨯=-=κλ3.解答：（1） 由玻耳兹曼定律可得TE E e g n g n κ121122//--=，且214g g =，202110=+n n 代入上式可得：≈2n 30（个）（2）)(10028.5)(1091228W E E n p -⨯=-= 4.解答：(1) 由教材（1-43）式可得317336343/10860.3/)106000.0(1063.68200018q m s J m s J h q ⋅⋅=⋅⋅⋅⋅⋅⋅=⋅=---πλπρν自激 （2）9344363107.5921063.68100.5)106328.0(8q ⋅=⋅⋅⋅⋅⋅==---ππρλνh q 自激5.解答：（1）红宝石半径cm r 4.0=，长cm L 8=，铬离子浓度318102-⋅=cm ρ，发射波长m 6106943.0-⋅=λ，巨脉冲宽度ns T 10=∆则输出最大能量)(304.2)(106943.0100.31063.684.0102)(68342182J J hcL r E =⋅⋅⋅⋅⋅⋅⋅⋅⋅==--πλπρ 脉冲的平均功率： )(10304.2)(1010304.2/89W W T E p ⋅=⋅=∆=- （2）自发辐射功率)(10304.2)(10106943.0)84.0102(100.31063.6)(22621883422W W L r hc hcN Q ⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅==---πλτπρλτ＝自6.解答：由λν/c =，λλνd cd 2=及λρνρλd d v =可得1185-==kThcehcd d λνλλπλνρρ7.解答： 由0)(=ννρd d 可得： 31=-kTh kTh m m mee kTh υυυ；令x kTh m=υ，则)1(3-=x x e xe ；解得：82.2=x 因此：1182.2--=kh T m ν 同样可求得：96.4=kThcm λ 故c m m 568.0=λν8解答：)]4(2[)(11)](4[114)(04042)(4202000πτνππτπτπτνννπττννπτνπτνννπτ--==+=-+=∞-∞∞-=-∞⎰⎰⎰arctg A x arctg A dxx A d A d f xN 令又04πτν数量级在810，所以2~)4(0ππτν--arctg ,代入上式得：τ/1=A9解答：由教材的（1-26）式可得：t A e n t n 21202)(-=，令en t n 1)(202=，则 21211,1A A ==ττ 10解答：相对论四维波矢量为：),(cik k ωμ = 对沿x 方向的特殊洛伦兹变换,有).(,,),(1'3'32'221'1k k k k k c k k υωγωωυγ-===-= (1)其中2211c υγ-=假设波矢量k 与x 轴的夹角为θ，'k 与x 轴的夹角为'θ，有'''11cos ,cos θωθωck ck == (2)代入（1）式可得)cos 1('θνωγωc-= (3)若'∑为光源的静止参考系，则0'ωω=。

思考练习题11． 试计算连续功率均为1W 的两光源，分别发射λ＝0.5000μm ，ν=3000MHz 的光，每秒从上能级跃迁到下能级的粒子数各为多少？答：粒子数分别为：188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2．热平衡时，原子能级E 2的数密度为n 2，下能级E 1的数密度为n 1，设21g g =，求：(1)当原子跃迁时相应频率为ν＝3000MHz ，T ＝300K 时n 2/n 1为若干。

(2)若原子跃迁时发光波长λ＝1μ，n 2/n 1＝0.1时，则温度T 为多高？答：（1）(//m n E E m m kTn n n g e n g --=）则有：1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν（2）K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3．已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0－18J ，设火焰(T ＝2700K)中含有1020个氢原子。

设原子按玻尔兹曼分布，且4g 1＝g 2。

求：(1)能级E 2上的原子数n 2为多少？(2)设火焰中每秒发射的光子数为l08 n 2，求光的功率为多少瓦？答：（1）1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n（2）功率＝W 918810084.51064.13110--⨯=⨯⨯⨯4．(1)普通光源发射λ＝0.6000μm 波长时，如受激辐射与自发辐射光功率体密度之比q q 激自1=2000，求此时单色能量密度νρ为若干？(2)在He —Ne 激 光器中若34/100.5m s J ⋅⨯=-νρ，λ为0.6328μm ，设μ＝1，求q q 激自为若干？ 答：（1）（2）943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q ＝自激5．在红宝石Q 调制激光器中，有可能将全部Cr 3＋(铬离子)激发到激光上能级并产生巨脉冲。

思考练习题11． 试计算连续功率均为1W 的两光源，分别发射λ＝0.5000μm ，ν=3000MHz 的光，每秒从上能级跃迁到下能级的粒子数各为多少？答：粒子数分别为：188346341105138.21031063.6105.01063.61⨯=⨯⨯⨯⨯=⨯⨯==---λνc h q n 239342100277.51031063.61⨯=⨯⨯⨯==-νh q n2．热平衡时，原子能级E 2的数密度为n 2，下能级E 1的数密度为n 1，设21g g =，求：(1)当原子跃迁时相应频率为ν＝3000MHz ，T ＝300K 时n 2/n 1为若干。

(2)若原子跃迁时发光波长λ＝1μ，n 2/n 1＝0.1时，则温度T 为多高？答：（1）(//m n E E m m kTn n n g e n g --=）则有：1]3001038.11031063.6exp[2393412≈⨯⨯⨯⨯⨯-==---kT h e n n ν（2）K T Te n n kT h 3623834121026.61.0]1011038.11031063.6exp[⨯=⇒=⨯⨯⨯⨯⨯⨯⨯-==----ν3．已知氢原子第一激发态(E 2)与基态(E 1)之间能量差为1.64×l0－18J ，设火焰(T ＝2700K)中含有1020个氢原子。

设原子按玻尔兹曼分布，且4g 1＝g 2。

求：(1)能级E 2上的原子数n 2为多少？(2)设火焰中每秒发射的光子数为l08 n 2，求光的功率为多少瓦？答：（1）1923181221121011.3]27001038.11064.1exp[4----⨯=⨯⨯⨯-⨯=⇒=⋅⋅n n e g n g n kTh ν且202110=+n n 可求出312≈n（2）功率＝W 918810084.51064.13110--⨯=⨯⨯⨯4．(1)普通光源发射λ＝0.6000μm 波长时，如受激辐射与自发辐射光功率体密度之比q q 激自1=2000，求此时单色能量密度νρ为若干？(2)在He —Ne 激光器中若34/100.5m s J ⋅⨯=-νρ，λ为0.6328μm ，设μ＝1，求q q 激自为若干？ 答：（1）3173436333/10857.31063.68)106.0(2000188m s J h h c q q ⋅⨯=⇒⨯⨯⨯=⇒=---ννννρρπρπλρνπ＝自激（2）943436333106.71051063.68)106328.0(88⨯=⨯⨯⨯⨯⨯==---πρπλρνπννh h c q q ＝自激5．在红宝石Q 调制激光器中，有可能将全部Cr 3＋(铬离子)激发到激光上能级并产生巨脉冲。

激光基横模TEM00高斯光束的振幅分布模拟激光基横模tem00高斯光束振幅分布的模拟1、激光基横模tem00高斯光束原理作为光源的激光器与普通光源之间的主要区别之一是激光器具有谐振腔。

谐振腔的主要功能是：将激光增益介质的受激放大长度相乘，形成高亮度的光；提高了光源的方向性；由于激光谐振腔中存在离散振荡模式，输出激光的单色性大大提高，实现了高相干性，改变了输出激光的光束结构和传输特性。

光学谐振腔是由相隔一定距离的两块反射镜组成的（一块全反射镜，一块部分反射镜）。

谐振腔靠两端的反射竟来实现光束在腔内的往返传播，对于光波没有任何其他限制，由于反射镜大小有限，它在对光束起反射作用的同时，还会引起光波的衍射效应。

腔内的光束每经过一次反射镜的作用，就使光束的一部分不能再次被反射回腔内。

因而，反射回来的光束的强度要减弱，同时光强分布也将发生变化。

当反射次数足够多时（大约三百多次反射）,光束的横向场分布便趋于稳定，不在受衍射的影响。

场分布腔内往返传播一次后能够再现出来。

反射只改变强度的大小，而不改变光的强度分布。

这种稳态场经一次往返后，唯一的变化是，镜面上各点的场振幅按同样的比例衰减，各点的相位发生同样大小的滞后，当两镜面完全相同时（对称开腔），这种稳态场分布应在腔内经单程渡越（传播）后即实现再现，这个稳定的横向场分布，就是激光谐振腔的自再现模。

通常叫作横模。

（1）自再现模（横模）积分方程陈佳碧和彭润玲出版了《激光原理与应用》第二版自再现模所足的积分方程为σ锰μmn（x，y）=∫∫k（x,y,x@,y@）μik2πlmn（x@，y@）ds@式中k（x,y,x@,y@）=σmne？ikρ（x，y，x'，y'）=iλle?ikρ(x,y,x',y')μmn的下标表示该方程存在一系的不连续的本征函数解与Mn特征值解。

积分方程μ的本征函数解一般是复函数，其模表示mn对称开腔任一镜面上的光场振幅分布。