2011届高三数学第一次模拟测试题6

xy OAC y x=2y x =(1,1)B丰台区2011年高三年级第二学期统一练习（一）数 学（理科）2011.3一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合U =R ，2{560}A x x x =-+≥，那么U A =ð(A) {2x x <或3}x > (B) {23}x x << (C) {2x x ≤或3}x ≥ (D) {23}x x ≤≤2．6的展开式中常数项是 (A) -160(B) -20(C) 20(D) 1603．已知平面向量a ，b 的夹角为60°，=a ，||1=b ，则|2|+=a b(A) 2(C)(D)4．设等差数列{}n a 的公差d ≠0，14a d =．若k a 是1a 与2k a 的等比中项，则k = (A) 3或-1 (B) 3或1(C) 3 (D) 1 5．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题： ① 若m β⊂，αβ⊥，则m α⊥； ② 若α//β，m α⊂，则m //β；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥． 其中正确命题的序号是 (A) ①③ (B) ①②(C)③④ (D) ②③6．已知函数3,0,()ln(1),>0.x x f x x x ⎧≤=⎨+⎩ 若f (2-x 2)>f (x )，则实数x 的取值范围是(A) (,1)(2,)-∞-⋃+∞(B) (,2)(1,)-∞-⋃+∞(C) (1,2)-(D ) (2,1)-7．从如图所示的正方形OABC 区域内任取一个点(,)M x y ，则点M 取自阴影部分的概率为(A) 12 (B)13 (C) 14(D) 168．对于定义域和值域均为[0，1]的函数f (x )，定义1()()f x f x =，21()(())f x f f x =，…，1()(())n n f x f f x -=，n =1，2，3，…．满足()n f x x =的点x ∈[0，1]称为f 的n 阶周期点．设12,0,2()122,1,2x x f x x x ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩ 则f 的n 阶周期点的个数是 (A) 2n(B) 2(2n -1)(C) 2n(D) 2n 2二、填空题：本大题共6小题，每小题5分，共30分．9．如图所示，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ， 点A 的纵坐标为45，则cos α= ． 10．双曲线的焦点在x 轴上，实轴长为4，离心率为3，则该双曲线的标准方 程为 ，渐近线方程为 ．11．已知圆M ：x 2+y 2-2x -4y +1=0，则圆心M 到直线43,31,x t y t =+⎧⎨=+⎩（t 为参数）的距离为 ．12．如图所示，过⊙O 外一点A 作一条直线与⊙O 交于C ，D 两点，AB 切⊙O 于B ，弦MN 过CD 的中点P ．已知AC =4，AB =6，则MP ·NP = ． 13．对某种花卉的开放花期追踪调查，调查情况如下：则这种卉的平均花期为___天． 14．将全体正奇数排成一个三角形数阵：1 3 5 7 9 11 13 15 17 19 ……按照以上排列的规律，第n 行（n ≥3）从左向右的第3个数为 ．NBAαxy O三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ． （Ⅰ）求角A 的大小； （Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC 的形状．16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABC D ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD（Ⅰ）若点M 是棱PC 的中点，求证：PA // 平面BMQ ； （Ⅱ）求证：平面PQB ⊥平面PAD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值 ．17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖． （Ⅰ）求分别获得一、二、三等奖的概率； （Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．PABCD QM18.（本小题共13分） 已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数． （Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值； （Ⅱ）若函数()'()axg x e f x -=⋅，求函数()g x 的单调区间．[来源:]19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P 满足||||PA PB +=，记动点P 的轨迹为W ． （Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．[来源:学&科&网]20.（本小题共13分）已知123{(,,,,)n n S A A a a a a == ，0i a =或1，1,2,,}i n = (2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值； （Ⅱ）令0(0,0,0,,0)n W =个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥；（Ⅲ）令123(,,,,)n U a a a a = ，若n V S ∈，求所有(,)d U V 之和．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011年高三年级第二学期数学统一练习（一）数 学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．35- 10．221432x y -=，y =± 11．212．25413．16天（15.9天给满分） 14．n 2-n +5 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b 2+c 2-a 2=bc ． （Ⅰ）求角A 的大小； （Ⅱ）设函数2cos 2cos 2sin 3)(2x x x x f +=，当)(B f 取最大值23时，判断△ABC 的形状．解：（Ⅰ）在△ABC 中，因为b 2+c 2-a 2=bc ，由余弦定理 a 2= b 2+c 2-2bc cos A 可得cos A =12．(余弦定理或公式必须有一个，否则扣1分) ……3分∵ 0<A <π ， （或写成A 是三角形内角） ………………4分∴3A π=． ……………………5分（Ⅱ）2cos 2cos 2sin 3)(2xx x x f +=11cos 22x x =++ ……………7分 1sin()62x π=++， …………………9分∵3A π= ∴2(0,)3B π∈PA BCDQM∴5666B πππ<+<（没讨论，扣1分） …………………10分 ∴当62B ππ+=，即3B π=时，()f B 有最大值是23． ……………………11分又∵3A π=， ∴3C π=∴△ABC 为等边三角形． ……………13分16.（本小题共14分）如图，在四棱锥P -ABCD 中，底面ABCD 为直角梯形，AD //BC ，∠ADC =90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA =PD =2，BC =12AD =1，CD（Ⅰ）若点M 是棱PC 的中点，求证：PA // 平面BMQ ； （Ⅱ）求证：平面PQB ⊥平面PAD ；（Ⅲ）若二面角M -BQ -C 为30°，设PM =tMC ，试确定t 的值 ． 证明：（Ⅰ）连接AC ，交BQ 于N ，连接MN ． ……………………1分∵BC ∥AD 且BC =12AD ，即BC //AQ ． ∴四边形BCQA 为平行四边形，且N 为AC 中点， 又∵点M 在是棱PC 的中点，∴ MN // PA ……………………2分 ∵ MN ⊂平面MQB ，PA ⊄平面MQB ，…………………3分 ∴ PA // 平面MBQ ． ……………………4分 （Ⅱ）∵AD // BC ，BC =12AD ，Q 为AD 的中点， ∴四边形BCDQ 为平行四边形，∴CD//BQ ． ……………………6分∵∠ADC =90° ∴∠AQB =90° 即QB ⊥AD ． 又∵平面PAD ⊥平面ABCD 且平面PAD ∩平面ABCD=AD ， ……………………7分∴BQ ⊥平面PAD ． ……………………8分∵BQ ⊂平面PQB ， ∴平面PQB ⊥平面PAD ． ……………………9分 另证：AD // BC ，BC =12AD ，Q 为AD 的中点 ∴ BC // DQ 且BC = DQ ，∴ 四边形BCDQ 为平行四边形，∴CD // BQ ． ∵ ∠ADC =90° ∴∠AQB =90°即QB ⊥AD ． ……………………6分∵ PA =PD ， ∴PQ⊥AD ． ……………………7分∵ PQ ∩BQ =Q ，∴AD ⊥平面PBQ ． ……………………8分∵ AD ⊂平面PAD ， ∴平面PQB ⊥平面PAD ． ……………………9分 （Ⅲ）∵PA =PD ，Q 为AD 的中点， ∴PQ ⊥AD ．∵平面PAD ⊥平面ABCD ，且平面PAD ∩平面ABCD=AD ， ∴PQ ⊥平面ABCD ．……………10分（不证明PQ ⊥平面ABCD 直接建系扣1分）如图，以Q 为原点建立空间直角坐标系．则平面BQC 的法向量为(0,0,1)n =；(0,0,0)Q ，P ，B，(C -分设(,,)M x y z ，则(,,PM x y z =- ，(1,)MC x y z=---，∵PM tMC = ，∴(1))(x t x yt y z t z =--⎧⎪=⎨⎪=-⎩）， ∴1t x t y z ⎧=-⎪+⎪⎪=⎨⎪⎪=⎪⎩……………………12分 在平面MBQ 中，QB = ，(1t QM t =-+ ， ∴平面MBQ法向量为)m t =．……………………13分∵二面角M -BQ -C 为30°， c o s 30n m n m ︒⋅===∴3t =． ……………………14分17.（本小题共13分）某商场在店庆日进行抽奖促销活动，当日在该店消费的顾客可参加抽奖．抽奖箱中有大小完全相同的4个小球，分别标有字“生”“意”“兴”“隆”．顾客从中任意取出1个球，记下上面的字后放回箱中，再从中任取1个球，重复以上操作，最多取4次，并规定若取出“隆”字球，则停止取球．获奖规则如下：依次取到标有“生”“意”“兴”“隆”字的球为一等奖；不分顺序取到标有“生”“意”“兴”“隆”字的球，为二等奖；取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖． （Ⅰ）求分别获得一、二、三等奖的概率； （Ⅱ）设摸球次数为ξ，求ξ的分布列和数学期望．解：（Ⅰ）设“摸到一等奖、二等奖、三等奖”分别为事件A ，B ，C ． ……1分则P (A )=111114444256⨯⨯⨯=，（列式正确，计算错误，扣1分） ………3分 P (B )33341-A =2565= （列式正确，计算错误，扣1分） ………5分三等奖的情况有：“生，生，意，兴”；“生，意，意，兴”；“生，意，兴，兴”三种情况． P (C )222444111*********()()()444444444444A A A =⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯964=．…7分（Ⅱ）设摸球的次数为ξ，则1,2,3ξ=． ……8分1(1)4P ξ==， 313(2)4416P ξ==⨯=，3319(3)44464P ξ==⨯⨯=，27(4)1(1)(2)(3)64P P P P ξξξξ==-=-=-==．（各1分）故取球次数ξ的分布列为…12分139271234 2.754166464E ξ=⨯+⨯+⨯+⨯=．(约为2.7) …13分18.（本小题共13分） 已知函数3211()(0)32f x x ax x b a =+++≥，'()f x 为函数()f x 的导函数． （Ⅰ）设函数f (x )的图象与x 轴交点为A ，曲线y =f (x )在A 点处的切线方程是33y x =-，求,a b 的值； （Ⅱ）若函数()'()axg x e f x -=⋅，求函数()g x 的单调区间．解：（Ⅰ）∵3211()(0)32f x x ax x b a =+++≥， ∴2'()1f x x ax =++． ……………………1分∵()f x 在(1,0)处切线方程为33y x =-，∴'(1)3(1)0f f =⎧⎨=⎩，……………………3分∴1=a ，611-=b ． （各1分） ……………………5分（Ⅱ）'()()ax f x g x e=21ax x ax e ++=()x R ∈．'()g x =22(2)(1)()ax axax x a e a x ax e e +-++2[(2)]ax x ax a e -=-+-． ……………………7分①当0a =时，'()2g x x =，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞． ……………………9分②当a >时，令'()0g x =，得x =或2x a a=- ……………………10分（ⅰ）当20a ->，即0a <<()g x 的单调递增区间为22(0,)a a -，单调递减区间为(,0)-∞，22(,)a a-+∞；……11分（ⅱ）当20a a-=，即a ='()g x =2220x x e -=-≤， 故()g x 在(,)-∞+∞单调递减； ……12分（ⅲ）当20a -<，即a >时，()g x 在22(,0)a a-上单调递增，在(0,)+∞，22(,)a a --∞上单调递 ………13分 综上所述，当0a =时，()g x 的单调递增区间为(0,)+∞，单调递减区间为(,0)-∞；当0a <<()g x 的单调递增区间为22(0,)a a-，单调递减区间为(,0)-∞，当a =()g x 的单调递减区间为(,)-∞+∞；当a >时，()g x 的单调递增区间为22(,0)a a-，单调递减区间为(0,)+∞，22(,)a a--∞．（“综上所述”要求一定要写出来）19.（本小题共14分）已知点(1,0)A -，(1,0)B ，动点P满足||||PA PB +=，记动点P 的轨迹为W ． （Ⅰ）求W 的方程；（Ⅱ）直线1y kx =+与曲线W 交于不同的两点C ，D ，若存在点(,0)M m ，使得CM DM =成立，求实数m 的取值范围．解：（Ⅰ）由椭圆的定义可知，动点P 的轨迹是以A ，B为焦点，长轴长为2分∴1c =，a =22b =． ……3分W 的方程是22132x y +=． …………4分（另解：设坐标1分，列方程1分，得结果2分）（Ⅱ）设C ，D 两点坐标分别为11(,)C x y 、22(,)D x y ，C ，D 中点为00(,)N x y ．由221132y kx x y =+⎧⎪⎨+=⎪⎩ 得 22(32)630k x kx ++-=． ……6分所以122632kx x k +=-+ …………7分 ∴12023232x x k x k +==-+， 从而0022132y kx k =+=+． ∴MN 斜率2002232332MN y k k k x m mk +==---+． ………9分 又∵CM DM =， ∴CD MN ⊥，∴222132332k k k m k +=---+ 即 232k m k =-+ …10分 当0k =时，0m =； ……11分当0k ≠时，212323k m k k k=-=-++]126,0()0,126[⋃-∈． ……13分故所求m 的取范围是]126,126[-． ……14分 （可用判别式法）20.（本小题共13分）已知123{(,,,,)n n S A A a a a a == ， 0i a =或1，1,2,}i n = (2)n ≥，对于,n U V S ∈，(,)d U V 表示U 和V 中相对应的元素不同的个数．（Ⅰ）令(0,0,0,0,0)U =，存在m 个5V S ∈，使得(,)2d U V =，写出m 的值； （Ⅱ）令0(0,0,0,,0)n W =个，若,n U V S ∈，求证：(,)(,)(,)d U W d V W d U V +≥；（Ⅲ）令123(,,,,)n U a a a a = ，若n V S ∈，求所有(,)d U V 之和． 解：（Ⅰ）2510C =； ………3分 （Ⅱ）证明：令123(,,)n u a a a a =……，123(,,)n v b b b b =……∵0i a =或1，0i b =或1；当0i a =，0i b =时，||i a +||0i b =||i i a b =- 当0i a =，1i b =时，||i a +||1i b =||i i a b =- 当1i a =，0i b =时，||i a +||1i b =||i i a b =- 当1i a =，1i b =时，||i a +||2i b =||0i i a b ≥-= 故||i a +||i b ||i i a b ≥-∴(,)(,)d u w d v w +=123()n a a a a ++ ++123()n b b b b +++ ++123(||||||)n a a a a =++ |++|123(||||||)n b b b b +++ |++|112233(||||||)n n a b a b a b a b ≥-+-+-- |++|(,)d u v = ………8分（Ⅲ）解：易知n S 中共有2n个元素，分别记为(1,2,,2)nk v k = 123(,,)n v b b b b =……∵0i b =的k v 共有12n -个，1i b =的k v 共有12n -个． ∴21(,)nkk d u v =∑=1111111122(2|0|2|1|2|0|2|120|21|)n n n n n n n n a a a a a a -------+-+-+--- |++|+|=12n n - ……13分∴21(,)nkk d u v =∑=12n n - ．法二：根据（Ⅰ）知使(,)k d u v r =的k v 共有rn C 个∴21(,)nkk d u v =∑=012012nn n n n CC C n C ++++21(,)nkk d u v =∑=120(1)(2)0nn n nn n n n Cn C n C C --+-+-++两式相加得 21(,)nkk d u v =∑=12n n -（若用其他方法解题，请酌情给分）。

合肥市2011年高三第一次教学质量检测数学试题(文)(考试时间：120分钟 满分：150分)注意事项：1．答题前，务必在试题卷、答题卡规定的地方填写自己的姓名、座位号，并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致.务必在答题卡背面规定的地方填写姓名和座位号后两位.2．答第I 卷时，每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号.3．答第Ⅱ卷时，必须使用0.5毫米的黑色墨水签字笔在答．题卡上．．．书写，要求字体工整、笔迹清晰，作图题可先用铅笔在答题卡．．．规定的位置给绘出，确认后再用0.5毫米的黑色墨水签字笔描清楚，必须在题号所指的答题区域作答，超出答题区域书写的答案无效，在试题卷．．．．．．．．．．．．．．．．．．、草稿纸上答题无效．．．．．．．．. 4.考试结束，务必将试题卷和答题卡一并上交.第Ⅰ卷 (满分50分)一、选择题(本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的)1.不等式201x x -+…的解集是 A.(,1)(1,2]-∞-- B.(1,2]- C.(,1)[2,)-∞-+∞ D.[1,2]- 2.复数21ia bi i=+-(i 是虚数单位，a 、b R ∈)，则 A.1a =，1b = B. 1a =-，1b =- C. 1a =-，1b = D. 1a =，1b =-3.“1a =”是“函数()lg()f x ax =在(0,)+∞单调递增”的A.充分不必要条件B.充分必要条件C.必要不充分条件D. 既不充分也不必要条件 4.以抛物线24y x =的焦点为圆心，半径为2的圆方程为A.22210x y x +--=B.22230x y x +--=C.22210x y x ++-=D.22230x y x ++-=5.右图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是 A.6π B.8π C. 12π D.24π6.为了从甲乙两人中选一人参加数学竞赛，老师将二人最近6次数学测试的分数进行统计，甲乙两人的平均成绩分别是x 甲、x 乙，则下列说法正确的是 A.x 甲>x 乙，乙比甲成绩稳定，应选乙参加比赛 B.x 甲>x 乙，甲比乙成绩稳定，应选甲参加比赛 C.x 甲<x 乙，甲比乙成绩稳定，应选甲参加比赛 D.x 甲<x 乙，乙比甲成绩稳定，应选乙参加比赛7.设a 、b 是两条不同直线，α、β是两个不同平面，则下列命题错误．．的是 A.若a α⊥，//b α，则a b ⊥ B.若a α⊥，//b a ，b β⊂,则αβ⊥ C.若a α⊥，b β⊥，//αβ,则//a b D.若//a α，//a β，则//αβ 8.已知函数()2sin()f x x ωϕ=+(0)ω>的图像关于直线3x π=对称，且()012f π=，则ω的最小值为A.2B.4C. 6D.89.{1,2,3}A =,2{|0,,}B x R x ax b a A b A =∈-+=∈∈,则A B B = 的概率是A.29B. 13C. 89D. 1 10.执行如边的程序框图，则输出的n = A.6 B.5 C.8 D.7第Ⅱ卷 (满分100分)二、填空题(本大题共5小题，每小题5分，共25分；把答案填在答题卡的相应位置) 11.若()33x x f x a -=+⋅是奇函数，则a =12.已知命题p ：(0)x R x ∀∈≠，12x x+…，则p ⌝：13.不等式组0 2 10x y x kx y ⎧⎪⎨⎪-+⎩………表示的是一个直角三角形围成的平面区域，则k =14.如图放置的边长为1的正方形ABCD 的顶点A 、D 分别在x 轴、y 轴正半轴上(含原点)上滑动，则OB OC ⋅的最大值是15.若曲线(,)0f x y =(或()y f x =)在其上两个不同点处的切线重合，则称这条切线为曲线(,)0f x y =(或()y f x =)的自公切线，下列方程的曲线存在自公切线的序号为 (填上所有正确的序号) ①2||y x x =- ②2||y x x =- ③3sin 4cos y x x =+④221x y -= ⑤||1x +=.三、解答题(本大题共6小题，共75分；解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内)16.(本小题满分12分)ABC ∆中，角A 、B 、C 所对应的边分别为a 、b 、c ，若sin sin sin a c Bb c A C-=-+. (1)求角A ；(2)若22()cos ()sin ()f x x A x A =+--，求()f x 的单调递增区间.17.(本小题满分12分)某种袋装产品的标准质量为每袋100克，但工人在包装过程中一般有误差，规定误差在2克以内的产品均为合格.由于操作熟练，某工人在包装过程中不称重直接包装，现对其包装(1)(2)估计该工人包装的产品的平均质量的估计值是多少. 18.(本小题满分12分)已知以1为首项的数列{}n a 满足：11()()2n n n a n a a n ++⎧⎪=⎨⎪⎩为奇数为偶数11a =，24a =，2123n n n a a a +++=*()n N ∈.(1)写出2a ，3a ，4a ，并求数列{}n a 的通项公式； (2)设数列{}n a 的前n 项和n S ，求数列{}n S 的前n 项和n T .19.(本小题满分12分)如图，长方体1111ABCD A B C D -中， 2DA DC ==，1DD =，E 是11C D 的中点，F 是CE 的中点.(1)求证：//EA 平面BDF ；(2)求证：平面BDF ⊥平面BCE .20.(本小题满分13分)椭圆的两焦点坐标分别为1(F和2F，且椭圆过点(1,. (1)求椭圆方程；(2)过点6(,0)5-作不与y 轴垂直的直线l 交该椭圆于M 、N 两点，A 为椭圆的左顶点，试判断MAN ∠的大小是否为定值，并说明理由．21.(本小题满分14分)已知函数()x f x e =，直线l 的方程为y kx b =+. (1)求过函数图像上的任一点(,())P t f t 的切线方程；(2)若直线l 是曲线()y f x =的切线，求证：()f x kx b +…对任意x R ∈成立； (2)若()f x kx b +…对任意[0,)x ∈+∞成立，求实数k 、b 应满足的条件.合肥市2011年高三第一次教学质量检测数学试题参考答案及评分标准二、填空题11.(理)24；(文)1-12.(理)22(1)4x y -+=；(文)(0)x R x ∃∈≠，12x x+< 13.(理)1±；(文)12-或014.215.(理)①③⑤；(文)①③ 三、解答题16.(文理)解：(1)由sin sin sin a c B b c A C -=-+，得a c bb c a c-=-+， 即222a b c bc =+-，由余弦定理，得1cos 2A =，∴3A π=； …………6分(2)22()cos ()sin ()f x x A x A =+--22cos ()sin ()33x x ππ=+--221cos(2)1cos(2)3322x x ππ++--=-1cos 22x =-…………9分 由222()k xk k Z πππ+∈剟，得()2k xk k Z πππ+∈剟，故()f x 的单调递增区间为[,]2k k πππ+，k Z ∈. …………12分17.解：(理)(1)由21230n n n a a a +++-=，得2112()n n n n a a a a +++-=-， ∴数列1{}n n a a +-就以213a a -=不首项，公比为2的等比数列，∴1132n n n a a -+-=⋅ …………3分 ∴2n …时，2132n n n a a ---=⋅，…，3232a a -=⋅，213a a -=， 累加得231132323233(21)n n n n a a ----=⋅+⋅+⋅⋅⋅+⋅+=-∴1322n n a -=⋅-(当1n =时，也满足) …………6分 (2)由(1)利用分组求和法得233(222)23(21)2n n n n S n n --=++⋅⋅⋅+-=-- …………9分3(21)2212n n S n n =-->-，得 3224n ⋅>，即3282n >=，∴3n >∴使得21n S n>-成立的最小整数4. …………12分 (文)(1)频率分布直方图如右 …………6分(2)112419296100104108100.2715551515⨯+⨯+⨯+⨯+⨯≈(克)…………12分18.(理)解：(1)12115155p =+= …………5分12141801234151551533E ξ=⨯+⨯+⨯+⨯+⨯= …………12分 (文)解：(1) 22a =，31a =，42a =， …………3分3(1)2nn a +-=， …………6分(2) 311[1(1)]311(1)222244n n n n n S ---=+⋅=-+- …………10分 ∴3(1)11[1(1)]224411n n n n T n +---=⋅-+⋅+ 23111(1)4288n n n =++⋅--(也可分n 奇数和偶数讨论解决) …………12分19.解：(文理)(1)连接AC 交BD 于O 点，连接OF ，可得OF 是ACE ∆的中位线，//OF AE ， 又AE ⊄平面BDF ，OF ⊂平面BDF ，所以//EA 平面BDF………(理)4分；(文)6分(2)计算可得2DE DC ==，又F 是CE 的中点，所以DF CE ⊥又BC ⊥平面11CDD C ，所以DF BC ⊥，又BC CE C = ，所以DF ⊥平面BCE 又DF ⊂平面BDF ，所以平面BDF ⊥平面BCE………(理)8分；(文)12分(3)(理)由(2)知DF ⊥平面BCE ，过F 作FG BE ⊥于G 点，连接DG ，则DG 在平面BCE 中的射影为FG ，从而DG BE ⊥，所以DGF ∠即为二面角D EB C --的平面角，设其大小为θ，计算得DF =2FG =，tan DF FGθ==…………12分20.解：(理)(1)设直线l 的方程为：2y kx =+(0)k ≠，联立方程可得224y kx y x =+⎧⎨=⎩得:22(44)40k x k x +-+=①设11(,)A x y ，22(,)B x y ，2(,0)C k -，则12244k x x k -+=-，1224x x k ⋅= ②21224(1)||||0|0|k MA MB x x k+⋅=--=，而222224(1)||0|)k MC k k+=--=，∴2||||||0MC MA MB =⋅≠， 即||MA ，||MC 、||MB 成等比数列 …………7分(2)由MA AC α= ，MB BC α=得，11112(,2)(,)x y x y k α-=---，22222(,2)(,)x y x y k β-=---即得：112kx kx α-=+，222kx kx β-=+，则212122121222()2()4k x x k x x k x x k x x αβ--++=+++由(1)中②代入得1αβ+=-，故αβ+为定值且定值为1- …………13分(文)(1)由题意，即可得到2214x y += …………5分(2)设直线MN 的方程为：65x ky =-，联立直线MN 和曲线C 的方程可得：226514x ky x y ⎧=-⎪⎪⎨⎪+=⎪⎩得：221264(4)0525k y ky +--=，设11(,)M x y ，22(,)N x y ，(2,0)A -，则122125(4)k y y k +=+，1226425(4)y y k ⋅=-+ 则211221212416(2,)(2,)(1)()0525AM AN x y x y k y y k y y ⋅=+⋅+=++++=即可得，2MAN π∠=. …………13分21.(理)证明(1)：∵()x f x e '=记切点为(,)t T t e ，∴切线l 的方程为()t t y e e x t -=-即(1)t t y e x e t =+- …………3分∴(1)t tk e b e t ⎧=⎨=-⎩记函数()()F x f x kx b =--,∴()(1)x t t F x e e x e t =--- ∴()x t F x e e '=-∴()F x 在(,)x t ∈-∞上为减，在(,)x t ∈+∞为增 故min ()()(1)0t t t F x F t e e t e t ==---=故()()0F x f x kx b =--…即()f x kx b +…对任意x R ∈成立 …………7分 (2)∵()f x kx b +…对任意x R ∈成立，即x e kx b +…对任意x R ∈成立 ①当0k <时，取0||10b x k+=<，∴001x e e <=，而0||11kx b b b +=++… ∴11x e kx b <+，∴0k <不合题意.②当0k =时，若0b …，则x e kx b +…对任意x R ∈成立若0b >取1ln 2b x =，∴12x be =，而1kx b b +=∴00x e kx b <+，∴0k =且0b >不合题意，故0k =且0b …不合题意……10分 ③当0k >时，令()x G x e kx b =--，()x G x e k '=-，由()0G x '=，得ln x k =， 所以()G x 在(,ln )k -∞上单减，(ln ,)k +∞单增 故()(ln )ln 0G x G k k k k b=--厖∴0 (1ln )k b k k >⎧⎨-⎩… …………13分综上所述：满足题意的条件是00k b =⎧⎨⎩…或0 (1ln )k b k k >⎧⎨-⎩… …………14分(文)解(1)：∵()x f x e '=，记切点为(,)t T t e ，∴切线l 的方程为()t t y e e x t -=- 即(1)t t y e x e t =+- …………3分(2)由(1)(1)t tk e b e t ⎧=⎨=-⎩ 记函数()()F x f x kx b =--,∴()(1)x t t F x e e x e t =--- ∴()x t F x e e '=-∴()F x 在(,)x t ∈-∞上单调递减，在(,)x t ∈+∞为单调递增 故min ()()(1)0t t t F x F t e e t e t ==---=故()()0F x f x kx b =--…即()f x kx b +…对任意x R ∈成立 …………8分 (3)设()()x H x f x kx b e kx b =--=--，[0,)x ∈+∞∴()x H x e k '=-，[0,)x ∈+∞ …………10分 ①当1k …时，()0H x '…，则()H x 在[0,)x ∈+∞上单调递增 ∴min ()(0)10H x H b ==-…，∴1b …，即11k b ⎧⎨⎩……符合题意②当1k >时，()H x 在[0,ln )x k ∈上单调递减，[ln ,)x k ∈+∞上单调递增 ∴min ()(ln )ln 0H x H k k k k b ==--…∴(1ln )b k k -… …………13分综上所述：满足题意的条件是11kb⎧⎨⎩……或1(1ln)kb k k>⎧⎨-⎩……………14分。

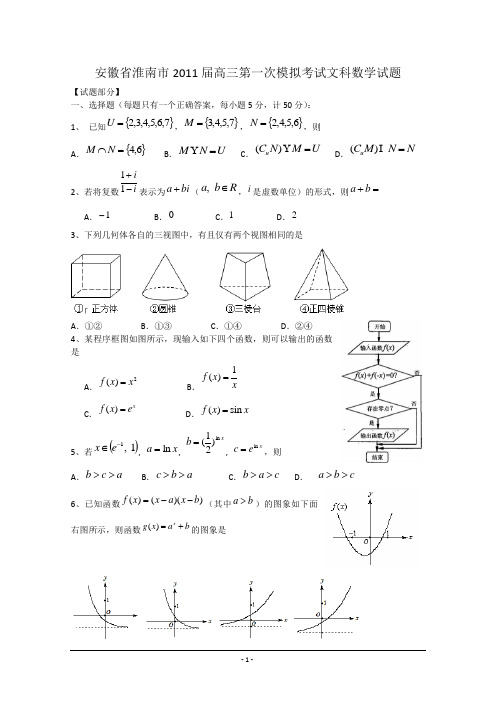
安徽省淮南市2011届高三第一次模拟考试文科数学试题【试题部分】一、选择题（每题只有一个正确答案，每小题5分，计50分）： 1、 已知{}7,6,5,4,3,2=U ，{}7,5,4,3=M ，{}6,5,4,2=N ，则A ．{}6,4=⋂NM B ．U N M = C ．U M N C u = )( D ．N N M C u = )(2、若将复数i i-+11表示为bi a +（R b a ∈,，i 是虚数单位）的形式，则=+b aA ．1-B ．0C ．1D ．23、下列几何体各自的三视图中，有且仅有两个视图相同的是A ．①②B ．①③C ．①④D ．②④4、某程序框图如图所示，现输入如下四个函数，则可以输出的函数是A ．2()f x x = B ．1()f x x =C ．()xf x e = D ．()sin f x x =5、若()1,1-∈e x , x a ln =,x b ln )21(=, xe c ln =，则 A ．a c b >> B ．a b c >> C ．c a b >> D ． c b a >>6、已知函数()()()f x x a x b =--（其中a b >）的图象如下面右图所示，则函数()xg x a b =+的图象是A ．B ．C ．D ．7、 抛物线21ym x =的准线与双曲线141222=-y x 的右准线重合,则m 的值是A. 8-B.12- C. 4 D. 168、若实数x ，y 满足不等式组：⎪⎩⎪⎨⎧≤-≥+-≥-3311y x y x y x ，则该约束条件所围成的平面区域的面积是A ．3B ．25C ．2D ．229、给出命题：（1）在空间里，垂直于同一平面的两个平面平行；（2）设m l ,是不同的直线，α是一个平面，若α⊥l ，l ∥m ，则α⊥m ； （3）已知βα,表示两个不同平面，m 为平面α内的一条直线，则“βα⊥”是“β⊥m ”的充要条件；（4）,a b 是两条异面直线，P 为空间一点, 过P 总可以作一个平面与b a ,之一垂直，与另一个平行。

2011届高三数学模拟试题（理科） 满分：150分 时间：120分钟一、选择题：本大题10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{0,1,2,3},{|2,}A B x x a a A ===∈集合，则（ ）A ．AB A = B ．A B A ÙC ．A B B =D ．A B A Ø2．命题p ：若0,a b a b ⋅<则与的夹角为钝角，命题q ：定义域为R 的函数()(,0)(0,)f x -∞+∞在及上都是增函数，则()(,)f x -∞+∞在 上是增函数下列说法正确的是 （ ） A ．“p 且q ”是假命题 B ．“p 或q ”是真命题C ．p ⌝为假命题D ．q ⌝为假命题3．函数sin (3sin 4cos )()y x x x x R =+∈的最大值为M ，最小正周期为T ，则有序数对（M ，T ）为 （ ）A ．(5,)πB ．(4,)πC ．(1,2)π-D ．(4,2)π4．“1a =-”是“直线260a x y -+=与直线4(3)90x a y --+=互相垂直”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．在ABC ∆中，角A 、B 、C 所对的边长分别为a 、b 、c ，若120,C c ==，则（ ）A ．45B > B ．45A >C ．b a >D ．b a <6．定义在区间(0,)a 上的函数2()2xx f x =有反函数，则a 最大为 （ ）A ．2ln 2B ．ln 22C ．12 D ．27．已知22(,)(3)1P x y x y +-=是圆上的动点，定点A （2，0），B （—2，0），则PA PB⋅ 的最大值为（ ）A ．4B ．0C ．—12D ．128．如图，在1,3ABC AN NC∆=中，P 是BN 上的一点， 若211AP mAB AC=+，则实数m 的值为（ ）A ．911B ．511C ．311D ．2119．设二次函数2()4()f x ax x c x R =-+∈的值域为19[0,),19c a +∞+++则的最大值为（ ）A ．3125B ．3833C ．65D ．312610．有下列数组排成一排：121321432114321(),(,),(,,),(,,,),(,,,,),112123123452345如果把上述数组中的括号都去掉会形成一个数列：121321132154321,,,,,,,,,,,,,,,112123423412345则此数列中的第2011项是（ ）A ．757B ．658C ．559D ．460二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡的相应位置。

武胜县2010秋高2011级联考数学（理）试卷考生注意：全卷满分150分，完成时间120分钟第Ⅰ卷 （选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1、求复数21()1i i-=+ （ ） A ． i B ． i - C ．1 D ． 1-2、“a b >”是 “22log log a b >”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3、已知函数21,(1)()1,(1)x x f x x a x -⎧≠⎪=-⎨⎪=⎩在R 上连续，则a =（ ）A ．13B ．1C ．12D ．04．若数列{}n a 的前n 项和为221n S n =-，则数列{}n a 的通项公式为( )A ．42n a n =-B ．42n a n =+C ． 1 14 2 2n n a n n =⎧=⎨+≥⎩D ． 1 14 2 2n n a n n =⎧=⎨-≥⎩5、200辆汽车经过某一雷达地区，时速频率分布直方图如图所示，则时速超过60 km/h 的汽车数量为（ ）A ．70B ．74C ．76D ．83 6．已知错误！不能通过编辑域代码创建对象。

，则错误！不能通过编辑域代码创建对象。

的值等于( )A ．错误！不能通过编辑域代码创建对象。

B ．-错误！不能通过编辑域代码创建对象。

C ．错误！不能通过编辑域代码创建对象。

D ．- 错误！不能通过编辑域代码创建对象。

7.定义在R 上的奇函数()f x 满足3()(),(1)12f x f x f =-+-=，则(1)(2)(f f f +++ = ( )A ． 1B ．2C ．1-D ． 08．设函数()sin cos =+f x x x x 的图像在点()(),t f t 处切线的斜率为k ，则函数()=k g t 的图像为（ ）9、给出下列命题：①存在实数x ，使3sin cos 2x x +=； ②若,αβ是第一象限角，且αβ>，则cos cos αβ<； ③函数2sin()32y x π=+是偶函数；④函数sin 24y x π⎛⎫=-⎪⎝⎭的图象向左平移4π个单位，得函数sin(2)4y x π=+的图象．其中正确命题的个数为（ ） A ． 1 B ．2 C ．3 D ． 410、数列{n a }中，1a =21，n n a a =+1+2312++n n （n )+∈N ，则n a =( ) A.11+=n a n B. 1+-=n n a n C. 1n na n =+ D. 11n a n =-+11、已知定义域为R 的函数()f x 在()1,+∞上为减函数，且函数(1)y f x =+为偶函数，则（ ）A ．(0)f ＞(1)fB ．(0)f ＞(2)fC ． (0)f ＞(3)fD ．(1)f -＜(4)f 12、已知函数32()(0)g x ax bx cx d a =+++≠的导函数为()f x ，0a b c ++=，且(0)(1)f f ∙＞0，设1x 、2x 是方程()0f x =的两个根，则12x x -的取值范围为（ ） A ．23⎫⎪⎪⎣⎭ B. 14,39⎡⎫⎪⎢⎣⎭C. 13⎡⎢⎣⎭D. 11,93⎡⎫⎪⎢⎣⎭武胜县2010年秋高2011级联考数学（理）试题一、选择题:本大题共12小题，每小题5分，共60分。

怀柔区2010～2011学年度第二学期高三适应性练习数 学（理科）2011.3本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分．考试时间120分钟．考试结束，将本试卷和答题卡一并交回．第Ⅰ卷（选择题 共40分）注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选 涂其它答案，不能答在试卷上．一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知全集R U =，}21{<<-=x x A ，}0{≥=x x B ，则=)(B A C UA ．}20{<≤x xB ．}0{≥x xC ．}1{-≤x xD ．}1{->x x2．复数=-+i i11A ．i -B ．1-C ．iD ．13．已知等比数列}{n a 的公比为2，且531=+a a ，则42a a +的值为A ．10B ．15C ．20D ．254．如图是一正方体被过棱的中点M 、N 和顶点A 、D 、C 1的两个截面截去两个角后所得的几何体，则该几何体的主视图为A ．B ．C ．D ． 5．若a ＝(1,2,－3)，b ＝(2,a －1,a 2－31)， 则“a ＝1”是“a ⊥b ”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．右图是计算函数2x ,x 1y 0,1x 2x ,x 2⎧-≤-⎪=-<≤⎨⎪>⎩的值的程序框图，则在①、②、③处应分别填入的是 A ．y x =-，y 0=，2y x =B ．y x =-，2y x =，y 0=C ．y 0=，2y x =，y x =-D ．y 0=，y x =-， 2y x =7．在极坐标系中，定点1,2A π⎛⎫⎪⎝⎭，动点B 在直线cos sinρθρθ+上运动，当线段AB 最短时，动点B 的极坐标是A ．)4,22(π B ．)43,22(πC ．)4,23(π D ．)43,23(π 8．已知三棱锥A BCO -，OA OB OC 、、两两垂直且长度均为6，长为2的线段MN 的一个端点M 在棱OA 上运动，另一个端点N 在BCO ∆内运动（含边界），则MN 的中点P 的轨迹与三棱锥的面所围 成的几何体的体积为A ．6π B ．6π或636π+C ．366π-D ．6π或366π-第Ⅱ卷（非选择题 共110分）注意事项：1．用钢笔或圆珠笔将答案直接写在试卷上． 2．答卷前将密封线内的项目填写清楚．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在题中横线上． 9．命题：0,2≥∈∀x R x 的否定是 ．10．函数1cos 2)(2-=x x f 的最小正周期为 ；单调递减区间为 ． 11．如图是甲、乙两班同学身高（单位：cm ）数据的茎叶图，则甲班同学身高的中位数为 ；若从乙班身高不低于170cm 的同学中随机抽取两名，则身高为173cm 的同学被抽中的概率为 ．甲班 乙班2 18 19 9 1 0 17 0 3 6 8 9 8 8 3 2 16 2 5 8 8 15 912．已知PA 是圆O 的切线，切点为A ，2=PA ．AC 是圆O 的直径，PC 与圆O 交于点B ，1=PB ，则圆O 的半径=R ．13．已知抛物线)0(22>=p px y 与双曲线12222=-by a x 有相同的焦点F ，点A 是两曲线的一个交点，且AF ⊥x 轴，则双曲线的离心率为 ．14注：加满油后已行驶距离加满油后已用油量油耗=，当前油耗汽车剩余油量可继续行驶距离=，指定时间内的行驶距离指定时间内的用油量平均油耗=．从以上信息可以推断在10：00—11：00这一小时内 （填上所有正确判断的序号）． ① 行驶了80公里； ② 行驶不足80公里；③ 平均油耗超过9.6升/100公里； ④ 平均油耗恰为9.6升/100公里； ⑤ 平均车速超过80公里/小时．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）在ABC ∆中，c b a 、、分别为角C B A 、、所对的三边，已知222+c b a bc -=． （Ⅰ）求角A 的值；（Ⅱ）若a =cos 3C =，求c 的长． 16．（本小题满分14分）如图，四棱锥P ABCD -的底面为正方形，侧棱PA ⊥底面ABCD ，且2P A A D ==，,,E F H分别是线段,,PA PD AB 的中点． （Ⅰ）求证：PB //平面EFH ； （Ⅱ）求证：PD ⊥平面AHF ； （Ⅲ）求二面角H EF A --的大小．17．（本小题满分13分）为了参加广州亚运会，从四支较强的排球队中选出18人组成女子排球国家队，队员来源人数如下（Ⅰ）从这18名队员中随机选出两名，求两人来自同一支队的概率；（Ⅱ）中国女排奋力拼搏，战胜韩国队获得冠军．若要求选出两位队员代表发言，设其中来自北京队的人数为ξ，求随机变量ξ的分布列，及数学期望ξE ．[来源:学科网][来源:学。

2011届北京市十一学校高三数学模拟练习班级__________姓名_______________2011.4.25出题人：贺思轩一、选择题1、设集合{}|23S x x=->，{}|8T x a x a =<<+，S T R = ，则a 的取值范围是（ A ） A ．13-<<-a B ．13-≤≤-aC ．3-≤a 或1-≥aD ．3-<a 或1->a 2、下列说法中，正确的是（ B ）A ．命题“若22am bm <，则a b <”的逆命题是真命题B ．命题“x R ∃∈，02>-x x ”的否定是：“x R ∀∈，02≤-x x ” C ．命题“p 或q ”为真命题，则命题“p ”和命题“q ”均为真命题 D ．已知R x ∈，则“1x >”是“2x >”的充分不必要条件3、若A 为不等式组002x y y x ≤≥≤⎧⎪⎨⎪-⎩表示的平面区域，则a 从-2连续变化到1时，动直线x y a +=扫过A 中的那部分区域的面积为（ D ）A ．913B ．313C ．72 D ．744、等差数列{}n a 的前n 项和为n S ，已知2110m m m a a a -++-=，2138m S -=，则m =（ C ）A ．38B ．20C ．10D ．95、已知甲、乙两车由同一起点同时出发，并沿同一路线（假定为直线）行驶．甲车、乙车的速度曲线分别为v v 乙甲和（如图2所示）．那么对于图中给定的01t t 和，下列判断中一定正确的是（ ） A ．在1t 时刻，甲车在乙车前面 B ．1t 时刻后，甲车在乙车后面 C ．在0t 时刻，两车的位置相同 D ．0t 时刻后，乙车在甲车前面【答案】：A ．由0()ts v t dt =⎰和定积分的几何意义，从图象中可直接得出在0t和1t 时刻，都有s s >乙甲．【评析】：本题考查定积分在物理中的运用以及定积分的几何意义．6、若直线1x ya b+=通过点()cos sin M αα，，则（ D ） A ．221a b +≤ B ．221a b +≥ C ．22111a b+≤D ．22111a b+≥ 7、有8张卡片分别标有数字1，2，3，4，5，6，7，8，从中取出6张卡片排成3行2列，要求3行中仅有中间行的两张卡片上的数字之和为5，则不同的排法共有（ A ）A ． 1344种B ． 1248种C ． 1056种D ． 960种8、如图，正方体1111ABCD A BC D -的棱线长为1，线段11B D 上有两个动点E ，F ，且2EF =，则下列结论中错误的是（ D ）A ．AC BE ⊥B ．//EF ABCD 平面C ．三棱锥A BEF -的体积为定值D ．异面直线AE BF ，所成的角为定值二、填空题9、已知()22a i i -=，其中i 是虚数单位，那么实数a = ．1-10、在极坐标系()ρθ，（02θπ≤≤）中，曲线2sin ρθ= 与cos 1ρθ=- 的交点的极坐标为______．3π⎫⎪⎭，4 11、如图，AB ，CD 是半径为a 的圆O 的两条弦，它们相交于AB 的中点P ，PD=23a ，∠OAP=30°，则CP ＝______．98a12、设()()2 01 0xa x f x f x x -⎧-≤⎪=⎨->⎪⎩，若方程()f x x =有且仅有两个实数解，则实数a 的取值范围是________．（－∞，2） 13、将函数2642--+=x x y [](0 6)x ∈，的图像绕坐标原点逆时针方向旋转角θ()0θα≤≤，得到曲线C ．若对于每一个旋转角θ，曲线C 都是一个函数的图像，则α的最大角的正切值为__________．1314、14、已知F 是椭圆2212x y +=的左焦点，P 和M 分别是椭圆2212x y +=和圆()()22:321A x y -+-=上的动点，PM PF +的最小值是______________________；||||PM PF -的最大值为________________．答案：1；1三、解答题15、设锐角三角形ABC 的内角A 、B 、C 的对边分别为a 、b 、c ，2sin a b A =． （Ⅰ）求B 的大小；（Ⅱ）求cos sin A C +的取值范围．解：（Ⅰ）由2sin a b A =，根据正弦定理得sin 2sin sin A B A =，所以1sin 2B =， 由ABC △为锐角三角形得π6B =． （Ⅱ）cos sin cos sin 6A C A A ππ⎛⎫+=+-- ⎪⎝⎭cos sin 6A A π⎛⎫=++ ⎪⎝⎭1cos cos 2A A A =++3A π⎛⎫=+ ⎪⎝⎭． 由ABC △为锐角三角形知，22A B ππ->-，2263B ππππ-=-=．2336A πππ<+<，所以1sin 23A π⎛⎫+< ⎪⎝⎭3A π⎛⎫<+< ⎪⎝⎭所以，cos sin A C +的取值范围为32⎫⎪⎪⎝⎭，．16、某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量（单位：克）重量的分组区间为（490，]495，（495，]500，……（510，]515，由此得到样本的频率分布直方图，如图所示．（1）根据频率分布直方图，求重量超过505克的产品数量．（2）在上述抽取的40件产品中任取2件，设Y 为重量超过505克的产品数量，求Y 的分布列． （3）从流水线上任取5件产品，求恰有2件产品的重量超过505克的概率． 简解：（1）重量超过505克的产品数量是()400.0550.015400.312⨯⨯+⨯=⨯=（件）（2）Y 的分布列为（3）2325373087*********C ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭17、如图，斜三棱柱111ABC A B C -的底面是直角三角形，90ACB ∠=︒，点1B 在底面ABC 上的射影恰好是BC 的中点，且1BC CA AA ==．（Ⅰ）求证：平面11ACC A ⊥平面11B C CB ； （Ⅱ）求证：1BC 1AB ⊥；（Ⅲ）求二面角11B AB C --的余弦值。

东城区2010-2011学年度综合练习（一）高三数学 （理科）学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题 共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）“2x >”是“24x >”的（A ）充分非必要条件 （B ）必要非充分条件 （C ）充要条件 （D ）既不充分也不必要条件（2）已知数列{}n a 为等差数列，且12a =，2313a a +=，那么则456a a a ++等于（A ）40 （B ）42 （C ）43 （D ）45（3）已知函数()f x 对任意的x ∈R 有()()0f x f x +-=，且当0x >时，()ln(1)f x x =+，则函数()f x 的大致图像为（C ） （D ） （4）已知平面上不重合的四点P ，A ，B ，C 满足0PA PB PC ++= ，且AB AC mAP +=，那么实数m 的值为（A ）2 （B ）3（C ）4 （D ）5（5）若右边的程序框图输出的S 是126，则条件①可为 A ．5n ≤ B ．6n ≤ C ．7n ≤ D ．8n ≤（6）已知(,)2απ∈π,1tan()47απ+=,那么ααcos sin +的值为 （A ）51- （B ）57（C ）57-（D ）43 （7）已知函数31)21()(x x f x-=，那么在下列区间中含有函数)(x f 零点的是（A ）)31,0( （B ）)21,31( （C ）)32,21( （D ）)1,32(（8）空间点到平面的距离定义如下：过空间一点作平面的垂线，这个点和垂足之间的距离叫做这个点到这个平面的距离．已知平面α，β，γ两两互相垂直，点A ∈α，点A 到β，γ的距离都是3，点P 是α上的动点，满足P 到β的距离是到P 到点A 距离的2倍，则点P 的轨迹上的点到γ的距离的最小值是（A ） 33- （B ）323- （C ）36- （D ）340 50 60 70 80 90 体重(kg) 频率A第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

北京市西城区2011年高三一模试卷 数 学（理科）第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项. 1. 已知集合{5}A x x =∈<Z ，{20}B x x =-≥，则A B 等于 （A ）(2,5)（B ）[2,5)（C ）{2,3,4}（D ）{3,4,5}2．下列给出的函数中，既不是奇函数也不是偶函数的是 （A ）2xy =（B ）2y x x =-（C ）2y x =（D ）3y x =3. 设3log 2=a ，3log 4=b ，5.0=c ，则 （A ）a b c <<（B ）b c a <<（C ）c a b <<（D ）b a c <<4．设向量(1,sin )θ=a ，(3sin ,1)θ=b ，且//a b ，则cos 2θ等于 （A ）31-（B ）32-（C ）32 （D ）31 5. 阅读右侧程序框图，为使输出的数据为31， 则①处应填的数字为 （A ）4 （B ）5 （C ）6 （D ）76.已知函数①x x y cos sin +=，②x x y cos sin 22=，则下列结论正确的是（A ）两个函数的图象均关于点(,0)4π-成中心对称 （B ）两个函数的图象均关于直线4x π=-成中心对称（C ）两个函数在区间(,)44ππ-上都是单调递增函数（D ）两个函数的最小正周期相同7．已知曲线1:(0)C y x x=>及两点11(,0)A x 和22(,0)A x ，其中210x x >>.过1A ，2A 分别作x 轴的垂线，交曲线C 于1B ，2B 两点，直线12B B 与x 轴交于点33(,0)A x ，那么 （A ）312,,2x x x 成等差数列 （B ）312,,2x x x 成等比数列 （C ）132,,x x x 成等差数列 （D ）132,,x x x 成等比数列8．如图，四面体OABC 的三条棱OC OB OA ,,两两垂直，2==OB OA ,3=OC ，D 为四面体OABC 外一点.给出下列命题.①不存在点D ,使四面体ABCD 有三个面是直角三角形 ②不存在点D ,使四面体ABCD 是正三棱锥 ③存在点D ,使CD 与AB 垂直并且相等④存在无数个点D ,使点O 在四面体ABCD 的外接球面上 其中真命题的序号是 （A ）①②（B ）②③（C ）③（D ）③④第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9. 在复平面内，复数2i1i-对应的点到原点的距离为_____. 10.如图，从圆O 外一点P 引圆O 的切线PA 和割线PBC ，已知PA =4PC =，圆心O 到BC圆O 的半径为_____. 11.已知椭圆:C cos ,()2sin x y θθθ=⎧∈⎨=⎩R 经过点1(,)2m ，则m =______，离心率e =______.12.一个棱锥的三视图如图所示，则这个棱锥的体积为_____.13.某展室有9个展台，现有3件展品需要展出，要求每件展品独自占用1个展台，并且3件展品所选用的展台既不在两端又不相邻，则不同的展出方法有______种；如果进一步要求3OABDC正(主)视图俯视图侧(左)视图件展品所选用的展台之间间隔不超过两个展位，则不同的展出方法有____种.14.已知数列{}n a 的各项均为正整数，对于⋅⋅⋅=,3,2,1n ，有1135,2n n n nn n kk a a a a a a +++⎧⎪=⎨⎪⎩为奇数为偶数.其中为使为奇数的正整数，, 当111a =时，100a =______；若存在*m ∈N ，当n m >且n a 为奇数时，n a 恒为常数p ，则p 的值为______.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）设ABC ∆中的内角A ，B ，C 所对的边长分别为a ，b ，c ，且54cos =B ,2=b . （Ⅰ）当35=a 时，求角A 的度数； （Ⅱ）求ABC ∆面积的最大值.16．（本小题满分13分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为11,,23p .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. （Ⅰ）求甲乙二人中至少有一人破译出密码的概率； （Ⅱ）求p 的值；（Ⅲ）设甲、乙、丙三人中破译出密码的人数为X ，求X 的分布列和数学期望EX .17.（本小题满分13分）如图, ABCD 是边长为3的正方形，DE ⊥平面ABCD ，DE AF //，AF DE 3=，BE 与平面ABCD 所成角为060.(Ⅰ)求证：AC ⊥平面BDE ； (Ⅱ)求二面角D BE F --的余弦值；（Ⅲ）设点M 是线段BD 上一个动点，试确定点M 的位置，使得//AM 平面BEF ，并证明你的结论.18. （本小题满分14分）已知函数2(1)()a x f x x -=，其中0a >. A BCD F E（Ⅰ）求函数()f x 的单调区间；（Ⅱ）若直线10x y --=是曲线()y f x =的切线，求实数a 的值； （Ⅲ）设2()ln ()g x x x x f x =-，求()g x 在区间[1,e ]上的最大值.（其中e 为自然对数的底数）19. （本小题满分14分）已知抛物线22(0)y px p =>的焦点为F ，过F 的直线交y 轴正半轴于点P ，交抛物线于,A B 两点，其中点A 在第一象限.（Ⅰ）求证：以线段FA 为直径的圆与y 轴相切；（Ⅱ）若1FA AP λ= ,2BF FA λ= ,1211[,]42λλ∈，求2λ的取值范围.20.（本小题满分13分）定义=),,,(21n a a a τ12231||||||n n a a a a a a --+-++- 为有限项数列{}n a 的波动强度.（Ⅰ）当(1)n n a =-时，求12100(,,,)a a a τ ；（Ⅱ）若数列,,,a b c d 满足()()0a b b c -->，求证：(,,,)(,,,)a b c d a c b d ττ≤； （Ⅲ）设{}n a 各项均不相等，且交换数列{}n a 中任何相邻两项的位置，都会使数列的波动强度增加，求证：数列{}n a 一定是递增数列或递减数列.用心 爱心 专心- 11 -。