湖北省恩施州高级中学2019-2020学年高一下学期期末考试数学试题

湖北省恩施市州高级中学2018-2019学年高一数学理期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 圆柱的侧面展开图是边长为4的正方形，则圆柱的体积是（）A. B.C. D.参考答案：B2. 当点到直线的距离最大时，m的值为（）A. 3B. 0C. －1D. 1参考答案：C【分析】求得直线所过的定点，当和直线垂直时，距离取得最大值，根据斜率乘积等于列方程，由此求得的值.【详解】直线可化为，故直线过定点，当和直线垂直时，距离取得最大值，故，故选C.【点睛】本小题主要考查含有参数的直线过定点的问题，考查点到直线距离的最值问题，属于基础题.3. （5分）如图，四棱锥S﹣ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（）A．AC⊥SBB．AB∥平面SCDC．AC⊥面SBDD．AB与SC所成的角等于DC与SA所成的角参考答案：D考点：直线与平面垂直的性质；棱锥的结构特征．专题：空间位置关系与距离．分析：A．利用正方形的性质和线面垂直的性质与判定即可得出；B．利用正方形的性质和线面平行的判定定理即可得出；C．通过平移即可得出异面直线所成的角；D．利用线面垂直的判定与性质、线面角的定义、等腰三角形的性质即可得出．解答：A．∵SD⊥平面ABCD，∴SD⊥AC．∵四边形ABCD是正方形，∴AC⊥BD．又∵SD∩DB=D．∴AC⊥平面SDB，∴AC⊥SB．B．∵四边形ABCD是正方形，∴AB∥DC，又AB?平面SCD，CD?平面SCD，∴AB∥平面SCD．C．由A可知：AC⊥平面SDB．D．∵AB∥DC，∴∠SCD（为锐角）是AB与SC所成的角，∠SAB（为直角）是DC与SA所成的角；而∠SCD≠∠SAB．∴AB与SC所成的角等于DC与SA所成的角不正确；故选：D．点评：本题综合考查了空间位置关系和空间角、正方形的性质，考查了直线与平面垂直的性质，属于中档题．4. 设-是等差数列的前项和，, 则的值为（）A. B.C. D.参考答案：D5. 设函数在上是增函数，则的范围是（）A. .B.C.D.参考答案：略6. 一种专门侵占内存的计算机病毒，开机时占据内存2KB，然后每3分钟自身复制一次，复制后所占内存是原来的2倍，若该病毒占据64MB内存（1MB=210KB），则开机后经过（）分钟．A．45 B．44 C．46 D．47参考答案：A【考点】等比数列的通项公式．【分析】n个3分钟后，所占内存是原来的2n+1倍，从而应有2n+1=64×210=216，由此能求出结果．【解答】解：因为开机时占据内存2KB，然后每3分钟自身复制一次，复制后所占内存是原来的2倍，所以3分钟后占据内存22KB，两个3分钟后占据内存23KB，三个3分钟后占据内存24KB，故n个3分钟后，所占内存是原来的2n+1倍，则应有2n+1=64×210=216，∴n=15，15×3=45，故选：A．7. 给出以下命题①若则；②已知直线与函数，的图象分别交于两点，则的最大值为；③若是△的两内角，如果，则；④若是锐角△的两内角，则。

2020年7月湖北省高一年级统一联合测试数学试题本试题卷共4页，22题．全卷满分150分．考试用时120分钟．★预祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试卷纸和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．写在试题卷、草稿纸和答题卡上的非答题区域均无效．3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内．写在试题卷、草稿纸和答题卡上的非答题区域均无效．4．考试结束后，请将本试题卷和答题卡一并上交．一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集U R =，已知集合{}39A x x x =<≥或，集合{}B x x a =≥．若()UA B ≠∅，则a 的取值范围为（ ）A ．3a >B ．3a ≤C ．9a <D ．9a ≤2．已知复数z 满足()1i 4z +=（i 为虚数单位），则复数z （ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．已知()1sin 3πα+=，则3sin 22πα⎛⎫+=⎪⎝⎭（ ）A ．79-B ．79C ．D 4．有四个幂函数：①()2f x x -=；②()1f x x -=；③()3f x x =；④()13f x x =．某同学研究了其中的一个函数，他给出这个函数的三个性质：（1）偶函数；（2）值域是{},0y R y y ∈≠且；（3）在(),0-∞上是增函数．如果他给出的三个性质中，有两个正确，一个错误，则他研究的函数是（ ） A ．④ B ．③ C ．② D ．①5．齐王与田忌赛马，田忌的上等马优于齐王的中等马，但劣于齐王的上等马；田忌的中等马优于齐王的下等马，但劣于齐王的中等马；田忌的下等马劣于齐王的下等马．现从双方的马匹中随机各选一匹进行一场比赛，则田忌马获胜的概率为（ ） A ．16 B ．15 C ．14 D ．136．设锐角ABC 的三个内角分别为角A 、B 、C ，那么“2A B π+>”是“sin cos B A >”成立的（ ）A ．充分必要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件7．根据食物中维C 的含量可大致分为：含量很丰富：鲜枣、沙棘、猕猴桃、柚子，每100克中的维生素C 含量超过100毫克；比较丰富：青椒、桂圆、番茄、草莓、甘蓝、黄瓜、柑橘、菜花，每100克中维生素C 含量在50~100毫克；相对丰富：白菜、油菜、香菜、菠菜、芹菜、苋菜、菜苔、豌豆、豇豆、萝卜，每100克中维生素C 含量在30~50毫克．现从猕猴桃、柚子两种食物中测得每100克所含维生素C 的量（单位：mg ）得到茎叶图如图所示，则下列说法中不正确的是（ ）A ．猕猴桃的极差为32B ．猕猴桃的平均数小于柚子的平均数C ．猕猴桃的方差小于柚子的方差D ．柚子的中位数为121 8．设0.1log 2a =，30log 2b =，则（ ） A ．()423ab a b ab >+>B ．()234ab a b ab >+> C ．()234ab a b ab <+<D ．()423ab a b ab <+<9．已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足()()20a c b c -⋅-=，则c 的最大值是（ ）A B ．2 C ．2 D ．510．在正三棱锥S ABC -中，M 、N 分别是棱SC 、BC 的中点，且AM MN ⊥，若侧棱SA =，则正三棱锥S ABC -外接球的体积是（ ）A ． B.60π C ． D ．48π11．设点D 为ABC 的边AB 上一点，点P 为ABC 内一点，且分别满足关系212AD AB λλ+=+，1AP AD BC λλ=++，0λ>，则APD ABCS S的最大值为（ ）A． B．4 C．2 D．312．已知()f x 是定义在[]1,1-上的奇函数，对任意的1x ，[]21,1x ∈-，均有()()()()11221221x f x x f x x f x x f x +≥+．且当[]0,1x ∈时，()25x f f x ⎛⎫= ⎪⎝⎭，()()11f x f x =--，那么表达式1901913193202020202020202020f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-+-++-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭（ ） A ．654-B ．65-C ．1314-D ．1312-二、填空题：本大题共4小题，每小题5分，共20分．13．已知扇形的周长等于它所在圆的周长的一半，则这个扇形的圆心角是________弧度．14．如图，E 、F 分别是三棱锥P ABC -的棱AP 、BC 的中点，10PC =，6AB =，7EF =，则异面直线AB 与PC 所成的角为________．15．若正数a ，b 满足2ab =，则11112M a b=+++的最小值为________． 16．在ABC 中，A ∠，B ∠，C ∠对应边分别为a ，b ，c ，且5a =，4b =，()31cos 32A B -=，则ABC 的边c =________．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）已知命题:p 存在实数x R ∈，使210x ax -+≤成立． （1）若命题P 为真命题，求实数a 的取值范围；（2）命题:q 任意实数[]1,2x ∈，使2210x ax -+≤恒成立．如果p ，q 都是假命题，求实数a 的取值范围．18．（本小题满分12分）在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且cos23cos 10C C +-=． （1）求角C 的大小；（2）若3b a =，ABCsin A B ，求c 的值． 19．（本小题满分12分）如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面S AB 为等边三角形．4AB BC ==，2CD SD ==．（1）求证：AB SD ⊥；（2）求AB 与平面SBC 所成的角的正弦值． 20．（本小题满分12分）某种工程车随着使用年限的增加，每年的维修费用也相应增加、根据相关资料可知该种工程车自购入使用之日起，前5年中每年的维修费用如下表所示：（1）根据数据可知y 与x 具有线性相关关系，请建立y 关于x 的回归方程y bx a =+．（2）根据实际用车情况，若某辆工程车每年维修费用超过4万元时，可以申请报备更换新车，请根据回归方程预估一辆工程车一般使用几年后可以申请报备更换新车．参考公式：()()()1122211n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑，a y bx =-．21．（本小题满分12分）某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[]50,100内，发布成绩使用等级制，各等级划分标准见下表．规定：A ，B ，C 三级为合格等级，D 为不合格等级．为了解该校高三年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．按照[)50,60，[)60,70，[)70,80，[)80,90，[]90,100的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示（1）根据频率分布直方图，求成绩的中位数（精确到0.1）；（2）在选取的样本中，从A ，D 两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是A 等级的概率．22．（本小题满分12分）如图，ABCD 是边长为3的正方形，DE ⊥平面ABCD ，AF ⊥平面ABCD ，3DE =，1AF =（1）证明：平面//ABF 平面DCE ；（2）在DE 上是否存在一点G ，使平面FBG 将多面体ABCDEF 分成上下两部分的体积比为3:11？若存在，求出点G 的位置：若不存在，请说明理由．湖北省2019-2020学年高一下学期期末联考数学试题参考答案一、填空题．二、填空题 13．2π- 14．3π（或60︒) 15．23 16．6三、解答题17．（1）:p 存在实数x R ∈，使210x ax +≤-成立2402a a ≥⇔=-⇔≤∆-或2a ≥，∴实数a 的取值范围为(][),22,-∞-+∞.（2）:q 任意实数[]1,2x ∈，使12a x x≥+恒成立，[]1,2x ∈，1522x x ∴≤+≤，55224a a ≥∴⇒≥，由题p ，q 都是假命题，那它们的补集取交集()552,2,2,44⎛⎫⎛⎫--∞=- ⎪ ⎪⎝⎭⎝⎭，∴实数a 的取值范围52,4⎛⎫- ⎪⎝⎭．18．（1）cos23cos 10C C +-=，22cos 3cos 20C C ∴+-=，解得，cos 12C =或cos 2C =-（舍）而()0,C π∈所以3C π=．（2）因为3b a =，由余弦定理可得，2219223a a c aa +-⋅⋅=，整理可得，c =．由正弦定理可得，sin sin c aC A =si 2n a A=，所以in s A =，sin sin 3B A ==，故ABC 的面积为128s 2in sin A ab B C ==，2132a ⨯=，所以7a =，c ==19．（1）取AB 的中点E ，连接DE ，则四边形BCDE 为矩形，2DE CB ==，那么AB DE ⊥，而又三角形SAB 为等边三角形，所以AB SE ⊥，且SEDE E =，所以AB ⊥面SDE ，故AB SD ⊥.（2）由AB ⊥平面S DE 知，平面ABCD ⊥平面SDE ，作SF DE ⊥，垂足为F ﹐则SF ⊥平面ABCD，SESD SF DE==⨯FG BC ⊥，垂足为G ，则2FG DC ==． 连结SG ，则SG BC ⊥，又BC FG ⊥，SG FG G =，故BC ⊥平面SFG ，平面SBC ⊥平面SFG作FH SG ⊥，H 为垂足，则FH ⊥平面SBC，7FG SF FH SG ==⨯，即F 到平面SBC的距离为7， 由于//ED BC ，所以//ED 平面SBC ，故E 到平面SBC 的距离d也为7，设AB 与平面SBC 所成的角为α，则sin 7d EB α==． 20．（1）由题可得()11234535x =⨯++++=，()11.1 1.622.5 2.825y =⨯++++=， 511 1.12 1.6324 2.55 2.834.3i ii x y==⨯+⨯+⨯+⨯+⨯=∑，521149162555i i x ==++++=∑，所以1222134.35320.435553ni ii ni i x y nx yb x nx==--⨯⨯===-⨯-∑∑，20.4330.71a y bx =-=-⨯=，所以y 关于x 的线性回归方程为0.430.71y x =+．（2）由题329280.430.714784343x x x ⇒>=⇒+≥>，所以预计一般第8年后可以申请报备更换新车． 21．（1）根据频率分布直方图，计算成绩的中位数为0.22701073.90.56+⨯=.（2）由茎叶图知，A 等级的学生有3人，D 等级的学生有0.1505⨯=人， 记A 等级的学生为A 、B 、C 、D 等级的学生为d 、e 、f 、g 、h ，从这8人中随机抽取2人，基本事件是：AB 、AC 、Ad 、Ae 、Af 、Ag 、A h 、BC 、Bd 、Be 、Bf 、Bg 、Bh 、Cd 、Ce 、CF 、Cg 、Ch 、de 、df 、dg 、dh 、ef 、eg 、eh 、fg 、fh 、gh ，共28个； 至少有一名是A 等级的基本事件是：AB 、AC 、Ad 、Ae 、Af 、Ag 、Ah 、BC 、Bd 、Be 、Bf 、Bg 、Bh 、Cd 、Ce 、Cf 、Cg 、Ch ，共18个； 故所求的概率为1892814P ==． 22．（1）证明：DE ⊥平面ABCD ，AF ⊥平面ABCD ，//DE AF ∴，//AF ∴平面DCE ，ABCD 是正方形，//AB CD ，//AB ∴平面DCE ，AB AF A =，AB ⊂平面ABF ，AF ⊂平面ABF ，∴平面//ABF 平面DCE .（2）解：假设存在一点G ，过G 作//MG BF 交EC 于M ，连接BG ，BM ， 由()()()1333311213332322ABCDEF B ADEF B CDEV V V --+⨯⨯=+=⨯⨯+⨯⨯=. 设EG t =，则21392144GFBME B EFG B EGM V V V --=+=⨯=. 设M 到ED 的距离为h ，则331h EM t EC ==-，即32h t =， 则2133224EGMt St t ⨯=⨯=，21113933332344GFBME B EFG B EGM V V V t t --=+=⨯⨯⨯+⨯⨯=⨯， 即2230t t +-=解得1t =，或3t =-（舍），则存在点G ，满足1EG =，即G 为ED 的一个靠近E 点的三等分点时满足条件．。

湖北省恩施市州高级中学2019-2020学年高三数学文期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 下列命题中错误的是（）A．命题“若x2﹣5x+6=0，则x=2”的逆否命题是“若x≠2，则x2﹣5x+6≠0”B．命题“角α的终边在第一象限，则α是锐角”的逆命题为真命题C．已知命题p和q，若p∨q为假命题，则命题p与q中必一真一假D．命题“若x＞y，则x＞|y|”的逆命题是真命题参考答案：C【考点】四种命题．【分析】写出命题“若x2﹣5x+6=0，则x=2”的逆否命题，判断A正确；写出命题“角α的终边在第一象限，则α是锐角”的逆命题，并判断真假性；根据复合命题的真假性判断C错误；写出命题“若x＞y，则x＞|y|”的逆命题，并判断真假性．【解答】解：对于A，命题“若x2﹣5x+6=0，则x=2”的逆否命题是“若x≠2，则x2﹣5x+6≠0”，故A正确；对于B，命题“角α的终边在第一象限，则α是锐角”的逆命题是“角α是锐角，则角α的终边在第一象限”，它是真命题，故B正确；对于C，若命题p∨q为假命题，则命题p与q一真一假或都为假命题，故C错误；对于D，命题“若x＞y，则x＞|y|”的逆命题是：“若x＞|y|，则x＞y”，它是真命题，故D正确．故选：C．2. 设等差数列{a n}的前n项和为S n，若S8=32，则a2+a7=（）A． 1 B． 4 C．8 D．9参考答案：考点：等差数列的前n项和．专题：等差数列与等比数列．分析：利用等差数列的通项公式和前n项和公式求解．解答：解：∵等差数列{a n}的前n项和为S n，S8=32，∴，∴a2+a7=8．故选：C．点评：本题考查等差数列的两项和的求法，是基础题，解题时要注意等差数列的性质的合理运用．3. 展开式中项的系数是40，则实数m的值为（）A．B．2 C．D．±2参考答案：C展开式中x2项是由的展开式中常数项，由的展开式中二次项与的常数项所组成的.∵的展开式的通项公式为：T r+1=令3r﹣10=0，解得r=，不合题意，应舍去；令3r﹣10=2，解得r=4，∴的展开式中x2项的系数为2?（﹣m）4=40，即m4=4，解得m=±．故答案为：C4. 已知复数满足，为虚数单位，则共轭复数（）A. B. C. D.参考答案：C5. 如图所示的坐标平面的可行域内（包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（）A．B．C．4 D．参考答案：B【考点】简单线性规划．【分析】化目标函数为直线方程的斜截式，结合使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，可知直线y=﹣ax+z与图中AC边所在直线重合，由斜率相等求得a 值．【解答】解：如图，化目标函数z=ax+y（a＞0）为y=﹣ax+z，要使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则直线y=﹣ax+z与图中AC边所在直线重合，即﹣a=，∴a=．故选：B．【点评】本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题．6. 设点O在∆ABC的内部，且有+2+3=，则∆ABC的面积与∆AOC的面积的比为( )A．2 B．C．3 D．参考答案：C解：如图，设∆AOC=S，则∆OC1D=3S，∆OB1D=∆OB1C1=3S，∆AOB=∆OBD=1.5S．∆OBC=0.5S，T∆ABC=3S．选C．7. 已知球的半径是，三点都在球面上，两点和两点的球面距离都是，两点的球面距离是，则二面角的大小是（A）（B）（C）（D）参考答案：答案：C解析：已知球的半径是R=，三点都在球面上，两点和两点的球面距离都是，则∠AOB，∠AOC都等于，AB=AC，两点的球面距离是，∠BOC=，BC=1，过B做BD⊥AO，垂足为D，连接CD，则CD⊥AD，则∠BDC是二面角的平面角，BD=CD=，∴∠BDC=，二面角的大小是，选C.8. 已知，A∈（0，），则（）A.B． C．D．参考答案：答案：A解析：由sin2A＝2sinAcosA＝>0，又A∈（0，）所以A?（0，），所以sinA＋cosA>0又（sinA＋cosA）2＝1＋2sinAcosA＝故选A9. 已知集合,则(A) (B) (C) (D)参考答案：【知识点】交集的运算.A1A解析：因为，所以，故选A。

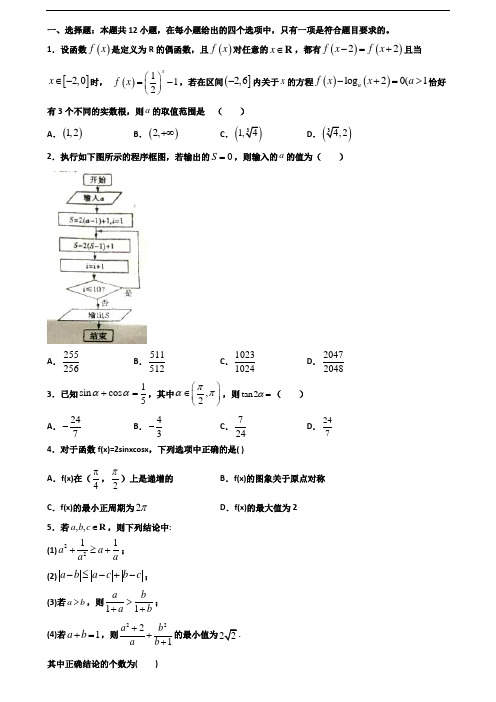
一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设函数()f x 是定义为R 的偶函数，且()f x 对任意的x ∈R ，都有()()22f x f x -=+且当[]2,0x ∈-时， ()112xf x ⎛⎫=- ⎪⎝⎭，若在区间(]2,6-内关于x 的方程()()log 20(1a f x x a -+=>恰好有3个不同的实数根，则a 的取值范围是 （ ） A ．()1,2B ．()2,+∞C ．()31,4D ．()34,22．执行如下图所示的程序框图，若输出的0S =，则输入的a 的值为（ ）A ．255256B ．511512C ．10231024D ．204720483．已知1sin cos 5αα+=，其中,2παπ⎛⎫∈ ⎪⎝⎭，则tan2α=（ ） A ．247-B ．43-C ．724D ．2474．对于函数f(x)=2sinxcosx ，下列选项中正确的是( ) A ．f(x)在（4π，2π）上是递增的 B ．f(x)的图象关于原点对称 C ．f(x)的最小正周期为2π D ．f(x)的最大值为25．若,,a b c ∈R ，则下列结论中: (1)2211a a a a+≥+； (2)a b a c b c -≤-+-； (3)若a b >，则11a ba b>++； (4)若1a b +=，则2221a b a b +++的最小值为22其中正确结论的个数为( )A ．1B ．2C ．3D ．46．已知直线倾斜角的范围是,32ππα⎡⎫∈⎪⎢⎣⎭2,23ππ⎛⎤⎥⎝⎦，则此直线的斜率的取值范围是（ ） A．⎡⎣B．(,-∞)+∞C．⎡⎢⎣⎦D．,⎛-∞ ⎝⎦⎫+∞⎪⎪⎣⎭7．在等差数列{}n a 中，n S 为其前n 项和，若34825a a a ++=，则9S =（ ） A ．60B ．75C ．90D ．1058．已知()y f x =是定义在R 上的奇函数，当0x <时，()2f x x =+，那么不等式2()10f x -<的解集是（） A ．5|02x x ⎧⎫<<⎨⎬⎩⎭B ．35| 022x x x ⎧⎫<-≤<⎨⎬⎩⎭或 C ．3|2x x ⎧⎫<-⎨⎬⎩⎭D ．35| 022x x x ⎧⎫<-<<⎨⎬⎩⎭或 9．已知方程22112x y m m+=--表示焦点在y 轴上的椭圆，则m 的取值范围是（ ）A ．(1,2)B ．31,2⎛⎫ ⎪⎝⎭C ．(,1)(2,)-∞⋃+∞D ．3(,1),2⎛⎫-∞⋃+∞ ⎪⎝⎭10． “αβ=”是“sin sin αβ=”成立的（） A ．充分非必要条件. B ．必要非充分条件. C ．充要条件.D ．既非充分又非必要条件.11．已知,a b 是平面内两个互相垂直的向量，且||1,||3a b ==，若向量c 满足()()0a c b c -⋅-=，则||c 的最大值是（ ） A ．1BC ．3D12．给出下列命题：（1）存在实数α使5sin cos 3αα+= . （2）直线20192x π=是函数cos y x =图象的一条对称轴. （3）()()cos sin y x x R =∈的值域是[]cos1,1.（4）若,αβ都是第一象限角，且sin sin αβ>，则tan tan αβ>. 其中正确命题的题号为（ ） A ．（1）（2）B ．（2）（3）C ．（3）（4）D ．（1）（4）二、填空题：本题共4小题 13．给出下列四个命题： ①在ABC ∆中，若2C π>，则sin cos A B <；②已知点()0,3A ，则函数3cos sin y x x =-的图象上存在一点P ，使得1PA =； ③函数2cos 2cos y x b x c =++是周期函数，且周期与b 有关，与c 无关； ④设方程sin 2x x π+=的解是1x ，方程arcsin 2x x π+=的解是2x ，则12x x π+=.其中真命题的序号是______.（把你认为是真命题的序号都填上） 14．在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，若3A π=，3a =，b=1,则c =_____________15．若arcsin 3arccos x x π+=，则实数x 的值为_______. 16．记n S 为数列{}n a 的前n 项和.若21n n S a =-，则n a =_______. 三、解答题：解答应写出文字说明、证明过程或演算步骤。

湖北省恩施土家族苗族自治州高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共27分)1. （2分） (2019高一下·哈尔滨月考) 已知向量，，，且，则实数（）A .B . 0C . 3D .2. （2分） (2020高三上·浙江开学考) 已知，，，则（）A .B .C .D .3. （2分）《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一，书中有这样的一道题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的是较小的两份之和，则最小的1份为（）A .B .C .D .4. （2分）中，若，则的形状为（）A . 直角三角形B . 等边三角形C . 等腰三角形D . 等腰直角三角形5. （5分） (2016高一下·吉林期中) 等比数列{an}中，a5=4，a7=6，则a9=（）A . 9B . ﹣9C . ﹣8D . 86. （2分） (2018高二下·温州期中) 已知变量满足约束条件 ,则的最小值为（）A .B .C .D .7. （2分）(2018·泸州模拟) 在梯形中，，， .将梯形绕所在的直线旋转一周而形成的曲面所围成的几何体的表面积为（）A .B .C .D .8. （2分） (2016高二上·开鲁期中) 已知| |=1，| |=2，且与夹角为60°，则等于（）A . 1B . 3C . 2﹣D . 4﹣9. （2分）如图是由一些相同的小正方体构成的主体图形的三种视图，构成这个立体图形的小正方体的个数是（）A . 3B . 4C . 5D . 610. （2分） (2016高二上·三原期中) 设△ABC，bcosC+ccosB=asinA，则△ABC的形状为（）A . 锐角三角形B . 直角三角形C . 钝角三角形D . 不确定11. （2分）下列函数中，最小值为4的是（）A .B .C .D .12. （2分）(2014·安徽理) 在平面直角坐标系xOy中．已知向量、，| |=| |=1，• =0，点Q满足 = （ + ），曲线C={P| = cosθ+ sinθ，0≤θ≤2π}，区域Ω={P|0＜r≤||≤R，r＜R}．若C∩Ω为两段分离的曲线，则（）A . 1＜r＜R＜3B . 1＜r＜3≤RC . r≤1＜R＜3D . 1＜r＜3＜R二、填空题 (共4题；共12分)13. （1分） (2019高三上·东台月考) 已知的夹角是钝角，则实数x的取值范围是________．14. （5分） (2019高一上·蓟县月考) 已知，的最小值为________.15. （1分） (2018高一下·枣庄期末) 如图，为测得河对岸塔的高，先在河岸上选一点，使在塔底的正东方向上，测得点的仰角为，再由点沿北偏东方向走米到位置，测得，则塔的高是________米．16. （5分） (2018高二上·潍坊月考) 已知，，且，则的最大值为________．三、解答题 (共6题；共60分)17. （10分） (2018高一下·长春期末) 已知三点,其中 .（1）若三点在同一条直线上,求的值；（2）当时,求 .18. （10分） (2016高二上·郑州期中) 已知关于x的不等式kx2﹣2x+3k＜0．（1）若不等式的解集为{x|x＜﹣3或x＞﹣1}，求k的值；（2）若不等式的解集为∅，求实数k的取值范围．19. （10分）(2017·黑龙江模拟) 已知数列{an}的前n项和为Sn ，满足，且a1=3．（Ⅰ）求数列{an}的通项公式；（Ⅱ）求证：．20. （10分）(2017·辽宁模拟) 如图，在直角梯形ABCD中AD∥BC．∠ABC=90°，AB=BC=2，DE=4，CE⊥AD 于E，把△DEC沿CE折到D′EC的位置，使D′A=2 ．（Ⅰ）求证：BE⊥平面AD′C；（Ⅱ）求平面D′AB与平面D′CE的所夹的锐二面角的大小．21. （10分） (2019高一下·南通月考) 在△ABC中，角A，B，C对应的边分别是a，b，c，已知cos2A﹣3cos （B+C）=1．（1）求角A的大小；（2）若△ABC的面积S=5 ，b=5，求sinBsinC的值．22. （10分） (2017高一下·长春期末) 数列{an}的前n项和为Sn ，且Sn=n（n+1）（n∈N*）（1）求数列{an}的通项公式；（2）若数列{bn}满足：an= + + +…+ ，求数列{bn}的通项公式；（3）令cn= （n∈N*），求数列{cn}的前n项和Tn ．参考答案一、单选题 (共12题；共27分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共12分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分) 17-1、17-2、18-1、18-2、19-1、20-1、21-1、21-2、22-1、22-2、22-3、。

湖北省恩施土家族苗族自治州 2019-2020 年度高一下学期期末数学试卷 C 卷姓名:________班级:________成绩:________一、 选择题 (共 12 题；共 24 分)1. （2 分） (2019 高一下·益阳月考) A. B.等于（ ）C.D. 2. （2 分） (2018·绵阳模拟) 为了解某高校高中学生的数学运算能力，从编号为 0001，0002，…，2000 的 2000 名学生中采用系统抽样的方法抽取一个容量为 50 的样本，并把样本编号从小到大排列，已知抽取的第一个样 本编号为 0003，则最后一个样本编号是（ ） A . 0047 B . 1663 C . 1960 D . 1963 3. （2 分） (2018 高一下·临沂期末) 一个扇形的弧长与面积都为 ，则这个扇形圆心角的弧度数为（ ） A. B. C.D. 4. （2 分） 某校女子篮球队 7 名运动员身高（单位：厘米）分布的茎叶图如图，已知记录的平均身高为 175cm，第 1 页 共 11 页但有一名运动员的身高记录不清楚，其末位数记为 ， 那么 的值为（ ）A.1B.2C.3D.45. （2 分） 如果若干个函数的图象经过平移后能够重合，则称这些函数为“互为生成函数”。

给出下列函数①；②；③；④其中“互为生成函数”的是（ ）A . ①②B . ①③C . ③④D . ②④6. （2 分） (2016 高一下·南市期中) 如果执行右边的程序框图，那么输出的 S=（ ）A . 10第 2 页 共 11 页B . 22 C . 46 D . 947. （2 分） (2019 高一上·田阳月考) 已知直线 一个单调递减区间是（ ）A. B. C. D. 8. （2 分） 函数 单位后，得到的图象解析式为（ ）是函数的一条对称轴，则的的部分图象如图示，则将 y=f(x)的图象向右平移 个A . y=sin2x B . y=cos2xC.D.9. （2 分） (2017 高一下·沈阳期末) 设中，内角 ， ， 所对的边分别为 ， ， ，且，则的最大值为（ ）A.第 3 页 共 11 页B.C.D.10. （2 分） 在平面上⊥，||=||=1， =+，| |＜ ，则||的取值范围（ ）A.B.C.D.11. （2 分） (2017·贵阳模拟) 已知向量 ， ，| |=2，| |=1，若 •（ ﹣ ）=2，则向 量 与 的夹角为（ ）A.B.C.D.12. （2 分） (2016 高二上·青浦期中) 若 Ai（i=1，2，3，…，n）是△AOB 所在平面内的点，且•= • ，给出下列说法：·（1）||=||=||=…=||第 4 页 共 11 页·（2）||的最小值一定是| |·（3）点 A 和点 Ai 一定共线·（4）向量及在向量方向上的投影必定相等其中正确的个数是（ ）A . 1个B . 2个C . 3个D . 4个二、 填空题 (共 4 题；共 4 分)13. （1 分） (2016 高三下·习水期中) 在△ABC 中，A=30°，2 余弦值为________．=3 2 ， 则△ABC 的最大角的14. （1 分） 有一根长度为 3 m 的绳子，拉直后在任意位置剪断，那么剪得的两段的长度都不小于 1 m 的概率 是________．15. （1 分） (2019 高一上·黄骅月考) 函数在区间[2，5]上的值域是________．16. （1 分） (2016 高一下·九江期中) 已知函数 f（x）= ①函数 f（x）的图象一定关于某条直线对称； ②函数 f（x）在 R 上是周期函数；③函数 f（x）的最大值为 ；（x∈R），给出下面四个命题：④对任意两个不相等的实数，都有第 5 页 共 11 页成立．其中所有真命题的序号是________．三、 解答题 (共 6 题；共 45 分)17. （5 分） (2018 高一下·黑龙江开学考) 已知点的坐标分别是，且.若，求的值.18. （5 分） (2017 高二上·荆门期末) 某网站对“爱飞客”飞行大会的日关注量 x（万人）与日点赞量 y（万 次）进行了统计对比，得到表格如下：x35679 y23345由散点图象知，可以用回归直线方程来近似刻画它们之间的关系．（Ⅰ）求出 y 关于 x 的回归直线方程，并预测日关注量为 10 万人时的日点赞量；（Ⅱ）一个三口之家参加“爱飞客”亲子游戏，游戏规定：三人依次从装有 3 个白球和 2 个红球的箱子中不放 回地各摸出一个球，大人摸出每个红球得奖金 10 元，小孩摸出 1 个红球得奖金 50 元．求该三口之家所得奖金总额 不低于 50 元的概率．参考公式：b=；参考数据：=200，=112．19. （5 分） 天气预报显示，在今后的三天中每天下雨的概率均为 30%．如果利用计算器或计算机产生 0～9 之间取整数值的随机数，我们再用 1，2，3 表示下雨，4，5，6，7，8，9，0 表示不下雨，以体现下雨概率为 30%， 于是得到 20 组随机数如下：907 191 537 764 120 734 257 055 458 271866 259 309 113 444 072 876 770 681 704那么，这三天中恰有两天下雨的概率是多少？20. （10 分） (2017 高一上·石家庄期末) 如图，点 A，B 是单位圆 O 上的两点，A，B 点分别在第一，而象限， 点 C 是圆 O 与 x 轴正半轴的交点，若∠COA=60°，∠AOB=α，点 B 的坐标为（﹣ ， ）．第 6 页 共 11 页（1） 求 sinα 的值； （2） 已知动点 P 沿圆弧从 C 点到 A 点匀速运动需要 2 秒钟，求动点 P 从 A 点开始逆时针方向作圆周运动时， 点 P 的纵坐标 y 关于时间 t（秒）的函数关系式． 21. （10 分） (2019 高一下·蛟河月考) 计算（1）；（2）22. （10 分） (2017·闵行模拟) 如图，某污水处理厂要在一个矩形 ABCD 的池底水平铺设污水净化管道（直 角△EFG，E 是直角顶点）来处理污水，管道越长，污水净化效果越好，设计要求管道的接口 E 是 AB 的中点，F、G分别落在 AD、BC 上，且 AB=20m，，设∠GEB=θ．（1） 试将污水管道的长度 l 表示成 θ 的函数，并写出定义域； （2） 当 θ 为何值时，污水净化效果最好，并求此时管道的长度．第 7 页 共 11 页一、 选择题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第 8 页 共 11 页16-1、三、 解答题 (共 6 题；共 45 分)17-1、18-1、 19-1、 20-1、第 9 页 共 11 页20-2、 21-1、 21-2、 22-1、第 10 页 共 11 页22-2、第11 页共11 页。

湖北省恩施土家族苗族自治州2020年高一下学期数学期末考试试卷（I）卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2018高二上·重庆期中) 已知点点，则为A . 4B . 2C .D .2. （2分）经过点的直线的斜率等于1，则m的值为（）A . 1B . 4C . 1或3D . 1或43. （2分） (2018高二上·北京月考) 在空间直角坐标系中，点（-2,1,4）关于轴对称的点坐标是（）A . （-2 , 1 , -4）B . （2 , 1 , -4）C . （-2 , -1 , -4）D . （2 , -1 , 4）4. （2分）(2020·武汉模拟) 圆C1：x2+y2＝4与圆C2：x2+y2﹣4x+4y﹣12＝0的公共弦的长为（）A .B .C .D .5. （2分）已知直线和平面满足,则（）A .B . 或C . 或D .6. （2分）方程表示圆的充要条件是A .B . 或C .D .7. （2分） (2017高二上·汕头月考) 若圆台的上下底面半径分别是1和3，它的侧面积是两底面面积的2倍，则圆台的母线长是（）A . 2B . 2.5C . 5D . 108. （2分） (2018高一下·西城期末) 方程表示的图形是（）A . 两个半圆B . 两个圆C . 圆D . 半圆9. （2分） (2018高二上·北京月考) 如下图是正方体的平面展开图，则在这个正方体中：①BM与ED平行②CN与BE是异面直线③CN与BM成60o角④DM与BN是异面直线以上四个命题中，正确命题的序号是（）A . ①②③B . ②④C . ③④D . ②③④10. （2分） (2019高二上·杭州期中) 三棱锥的高为，若三条侧棱两两垂直，则为的（）A . 内心B . 外心C . 垂心D . 重心二、填空题 (共6题；共7分)11. （2分） (2019高二上·宁波期中) 直线的斜率为________；倾斜角的大小是________．12. （1分） (2019高二上·南充期中) 已知直线平行，则________13. （1分） (2018高一下·黑龙江期末) 如图，在三棱锥中，平面， ,, ，则三棱锥外接球的表面积为________．14. （1分） (2017高二上·汕头月考) 直线，对任意直线恒过定点________．15. （1分）如图，在正方体中，E，F分别是棱BC，C1D1的中点，则EF与平面BDD1B1的位置关系是________.16. （1分）(2013·浙江理) 设F为抛物线C：y2=4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于________．三、解答题 (共3题；共30分)17. （10分） (2016高一上·西安期末) 如图，在直三棱柱ABC﹣A1B1C1中，AB=AC=5，BB1=BC=6，D，E分别是AA1和B1C的中点（1）求证：DE∥平面ABC；（2）求三棱锥E﹣BCD的体积．18. （10分） (2018高一下·安庆期末) 根据所给的条件求直线的方程：（1）直线过点（-4，0），倾斜角的正弦值为；（2）直线过点（5，10），到原点的距离为5.19. （10分）(2017高二上·哈尔滨月考) 如图,点是以为直径的圆周上的一点，, 平面，点为中点.（1）求证：平面平面；（2）求直线与平面所成角的大小.参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共7分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共3题；共30分)17-1、17-2、18-1、18-2、19-1、19-2、。

湖北省恩施土家族苗族自治州 2019 版高一下学期期末数学试卷（I）卷姓名:________班级:________成绩:________一、 选择题 (共 12 题；共 24 分)1. （2 分） 若角 α 的终边落在直线 y=2x 上，求 sin2α﹣cos2α+sinαcosα 的值（ ）A.1B.2C . ±2D . ±12. （2 分） (2016 高一上·荆门期末) 若一圆弧长等于它所在圆的内接正三角形的边长，则该弧所对的圆心 角弧度数为（ ）A.B.C. D.2 3. （2 分） 要得到函数的图像，只需将的图像（ ）A . 向左平移 个单位长度B . 向右平移 个单位长度C . 向左平移 个单位长度D . 向右平移 个单位长度 4. （2 分） 与向量 =（﹣5，4）平行的向量是（ ）第 1 页 共 11 页A . （﹣5k，4k）B . （﹣ ，﹣ ） C . （﹣10，2） D . （5k，4k）5. （2 分） 已知 A.2 B . ﹣2，那么的值为（ ）C.D . 2或6. （2 分） 在△ABC 中，若 = （ + ），则下列关系式正确的是（ ） A . BD=2CD B . BD=CD C . BD=3CD D . CD=2BD7. （2 分） 如图所示，角 θ 的终边与单位圆交于点 P（﹣ ， ），则 cos（π﹣θ）的值为（ ）A.B.第 2 页 共 11 页C.-D.8. （2 分） 命题 p:若 上都是增函数，则 f(x)在， 则 与 的夹角为钝角.命题 q：定义域为 R 的函数 f(x) 在及上是增函数. 下列说法正确的是A . “p 或 q”是真命题B . “p 且 q”是假命题C . 为假命题D . 为假命题9. （2 分） (2016 高一下·晋江期中) 若非零向量 ， 满足| |= （3 +2 ），则 与 的夹角为（ ）| |，且（ ﹣ ）⊥A.B.C. D.π10. （2 分） (2017 高一下·宜昌期末) 已知 cos（ ） ﹣cosα= ，则 cos（ ） 的值为（ ）A.B.﹣C.D.﹣ 11. （2 分） 函数是（）第 3 页 共 11 页A . 最小正周期为 的奇函数 B . 最小正周期为 的偶函数 C . 最小正周期为 的奇函数 D . 最小正周期为 的偶函数 12. （2 分） (2016·桂林模拟) 若向量 ， 满足：| |=1，（ + ）⊥ ，（3 + ）⊥ ， 则| |=（ ） A.3 B. C.1D.二、 填空题 (共 4 题；共 4 分)13. （1 分） (2017 高一上·南昌月考) 计算：的结果是________．14. （1 分） (2019 高一下·阜新月考) 如图，在矩形 ABCD 中，边 AB=5，AD=1，点 P 为边 AB 上一动点，当∠DPC 最大时，线段 AP 的长为________.15. （1 分） (2017·盐城模拟) 已知 A，B，C，D 四点共面，BC=2，AB2+AC2=20， 的最大值为________．，则| |16. （1 分） 如图，一艘轮船 B 在海上以 40nmile/h 的速度沿着方位角（从指北方向顺时针转到目标方向线的 水平角）为 165°的方向航行，此时轮船 B 的正南方有一座灯塔 A．已知 AB=800nmile，则轮船 B 航行________ h 时距离灯塔 A 最近．第 4 页 共 11 页三、 解答题 (共 6 题；共 55 分)17. （10 分） (2016 高三上·平罗期中) 已知向量 数 f（x）= • ．=（2sinx，（1） 求 f（x）的单调递增区间；cosx）， =（﹣sinx，2sinx），函（2） 求函数 f（x）在区间[0， ]的最值及所对应的 x 值．18. （10 分） 已知 f（α）=．（1） 化简 f（α）；（2） 若 f（α）= ，且 ＜α＜ ，求 cosα﹣sinα 的值．19. （10 分） 若 f（x）=Asin（ωx+θ）（A＞0，ω＞0，|θ|＜ ）的图象如图所示，（1） 求 f（x）的解析式． （2） 求 f（x）的单调区间及对称轴．20. （ 10 分 ） (2018 高 一 下 · 黑 龙 江 期 末 ) 已 知 向 量第 5 页 共 11 页，设．（1） 求函数的解析式及单调递增区间；（2） 在中，分别为内角的对边，且，求21. （5 分） 设△ABC 的内角 A，B，C 所对的边分别是 a，b，c，且 cosC+ =1． （1）求角 A 的大小； （2）若 a=1，求△ABC 的周长 l 的取值范围． 22. （10 分） (2017 高一上·吉林期末) 已知函数 f（x）=（sinx+cosx）2+2cos2x （1） 求函数 f（x）的最小正周期和单调减区间； （2） 求使 f（x）≥3 成立的 x 的取值集合．的面积．第 6 页 共 11 页一、 选择题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 6 题；共 55 分)17-1、17-2、 18-1、 18-2、第 8 页 共 11 页19-1、19-2、 20-1、第 9 页 共 11 页20-2、21-1、第 10 页 共 11 页22-1、22-2、第11 页共11 页。

2019-2020学年高一下学期期末数学模拟试卷一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．函数()1,0252sin 2,0,6x x f x x x ππ⎧≤⎪⎪=⎨⎛⎫⎪+<< ⎪⎪⎝⎭⎩，，若方程()f x a =恰有三个不同的解，记为123,,x x x ，则123x x x ++的取值范围是( )A ．10102,33ππ⎛⎫-⎪⎝⎭ B ．552,33ππ⎛⎫-⎪⎝⎭C ．10101,33ππ⎛⎫-⎪⎝⎭ D ．551,33ππ⎛⎫-⎪⎝⎭2．在等差数列中，若，则（ ）A ．6B ．7C ．8D ．93．已知椭圆C ：22221(0)x y a b a b +=>>的左右焦点为F 1,F 2离心率为3过F 2的直线l 交C 与A,B 两点，若△AF 1B 的周长为3C 的方程为( )A ．22132x y +=B ．2213x y +=C ．221128x y +=D ．221124x y +=4．已知数列}{n a 满足111n n a a a +==，则10a =（ ） A ．10B ．20C ．100D ．2005．我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”，如30723=+．在不超过30的素数中，随机选取两个不同的数，其和等于30的概率是 A ．112B ．114C ．115D ．1186． “b 是13+13-”是“b 是23与23的等比中项”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件7．设函数()122,1 1,1x x f x log x x -⎧≤=⎨->⎩，则()()4f f =（ ）A ．2B ．4C ．8D ．168．已知ABC ∆中，10AB =，6AC =，8,BC M =为AB 边上的中点，则CM CA CM CB ⋅+⋅= ( ) A ．0B ．25C ．50D ．1009．已知x 与y 之间的几组数据如下表x0123y1-3-4-7-则y与x的线性回归方程ˆy bx a=+必过( )A．点()2,2B．点()1.5,4C．点()1.5, 3.75-D．点()1.5,010．设ABC∆的内角,,A B C所对边的长分别为,,a b c，若2,3sin5sinb c a A B+==,则角C=（）A．3πB．23πC．34πD．56π11．执行如图所示的程序语句，输出的结果为( )A．1011B．910C．190D．111012．已知z是z的共轭复数，若复数1222izi-=++，则z在复平面内对应的点是（）A．(2,1)B．(2,1)-C．(2,1)-D．(2,1)--二、填空题：本题共4小题13．现用一半径为10cm，面积为280cmπ的扇形铁皮制作一个无盖的圆锥形容器（假定衔接部分及铁皮厚度忽略不计，且无损耗），则该容器的容积为__________3cm.14．已知圆锥的底面半径为3，体积是12π，则圆锥侧面积等于___________.15．已知函数()y f x=是定义域为R的偶函数，当0x≥时，()sin,02432,24xx xf xxπ-⎧⎛⎫≤≤⎪⎪⎪⎝⎭=⎨⎪+>⎪⎩，若关于x的方程()()()255440f x a f x a-++=⎡⎤⎣⎦()a R∈有且仅有6个不同实数根，则实数a的取值范围为______.16．如图，长方体''''OABC D A BC-中，3OA=，4OC=，5OD'=，A C''与B D''相交于点P，则点P的坐标为______________．三、解答题：解答应写出文字说明、证明过程或演算步骤。