2016年中考数学考点总动员系列 专题32 图形的轴对称重点
- 格式:doc
- 大小:872.00 KB
- 文档页数:18

轴对称知识点总结1、轴对称图形:一个图形沿一条直线对折,直线两旁的局部能够完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
2、轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
3、轴对称图形与轴对称的区别与联系:1〕区别。
轴对称图形讨论的是“一个图形与一条直线的对称关系〞;轴对称讨论的是“两个图形与一条直线的对称关系〞。
2〕联系。
把轴对称图形中“对称轴两旁的局部看作两个图形〞便是轴对称;把轴对称的“两A'HID D'J B 'K C'个图形看作一个整体〞便是轴对称图形。
4、轴对称的性质:1〕成轴对称的两个图形全等。
2〕对称轴与连结“对应点的线段〞垂直。
3〕对应点到对称轴的距离相等。
4〕对应点的连线互相平行。
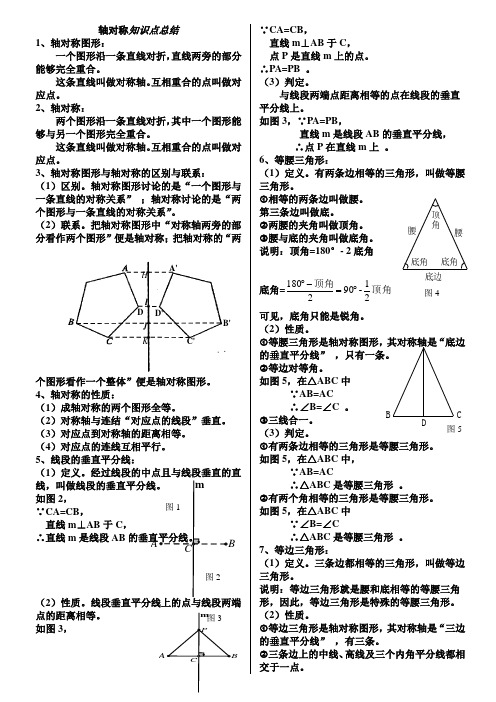
5、线段的垂直平分线:〔1〕定义。
经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
m如图2,图1∵CA=CB,直线m⊥AB于C,∴直线m是线段AB的垂直平分线。
A B C图〔2〕性质。
线段垂直平分线上的点与线段两端点的距离相等。
m图3如图3,P A BCCA=CB,直线m⊥AB于C,点P是直线m上的点。
∴PA=PB。
〔3〕判定。
与线段两端点距离相等的点在线段的垂直平分线上。
如图3,∵PA=PB,直线m是线段AB的垂直平分线,∴点P在直线m上。
6、等腰三角形:1〕定义。
有两条边相等的三角形,叫做等腰三角形。
相等的两条边叫做腰。
第三条边叫做底。
顶两腰的夹角叫做顶角。
腰角腰腰与底的夹角叫做底角。
说明:顶角=180°-2底角底角底角底角=180顶角1顶角底边90-图422可见,底角只能是锐角。
〔2〕性质。
等腰三角形是轴对称图形,其对称轴A是“底边的垂直平分线〞,只有一条。
等边对等角。
如图5,在△ABC中∵AB=AC∴∠B=∠C。
B C 三线合一。
D〔3〕判定。
图5有两条边相等的三角形是等腰三角形。
轴对称知识点总结1、轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
2、轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
3、轴对称图形与轴对称的区别与联系:(1)区别。
轴对称图形讨论的是“一个图形与一条直线的对称关系” ;轴对称讨论的是“两个图形与一条直线的对称关系”。
(2)联系。
把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称;把轴对称的“两个图形看作一个整体”便是轴对称图形。
4、轴对称的性质:(1)成轴对称的两个图形全等。
(2)对称轴与连结“对应点的线段”垂直。
(3)对应点到对称轴的距离相等。
(4)对应点的连线互相平行。
5、线段的垂直平分线:(1)定义。
经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
如图2,∵CA=CB ,直线m ⊥AB 于C ,∴直线m 是线段AB 的垂直平分线。
(2)性质。
线段垂直平分线上的点与线段两端点的距离相等。
如图3,∵CA=CB ,直线m ⊥AB 于C , 点P 是直线m 上的点。
∴PA=PB 。
(3)判定。
与线段两端点距离相等的点在线段的垂直平分线上。
如图3,∵PA=PB ,直线m 是线段AB 的垂直平分线, ∴点P 在直线m 上 。
6、等腰三角形:(1)定义。
有两条边相等的三角形,叫做等腰三角形。
①相等的两条边叫做腰。
第三条边叫做底。
②两腰的夹角叫做顶角。
③腰与底的夹角叫做底角。
说明:顶角=180°- 2底角底角=顶角顶角21-902180︒=-︒ 可见,底角只能是锐角。
(2)性质。
①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线” ,只有一条。
②等边对等角。
如图5,在△ABC 中 ∵AB=AC∴∠B=∠C 。
③三线合一。
(3)判定。
①有两条边相等的三角形是等腰三角形。
如图5,在△ABC 中, ∵AB=AC∴△ABC 是等腰三角形 。

中考复习图形的对称知识点总结含考点,中考真题图形的对称【知识梳理】知识点⼀:图形的轴对称1.轴对称图形的概念:如果⼀个图形沿着⼀条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.2.轴对称的概念:把⼀个图形沿着某⼀条直线翻折过去,如果它能够和另⼀个图形重合,那么这两个图形关于直线对称,两个图形关于直线对称也称轴对称.这条直线叫做对称轴.3.轴对称变换的基本性质(1)对应点所连的线段被对称轴垂直平分;(2)对应线段相等,对应⾓相等.4.轴对称和轴对称图形的区别:轴对称涉及两个图形,是两个图形的位置关系;轴对称图形是对⼀个图形本⾝⽽⾔的.5.镜⾯对称原理(1)镜中的像与原来的物体成轴对称.(2)镜⼦中的像改变了原来物体的左右位置,即像与物体左右位置互换.重点:轴对称的认识难点:对称轴在实际⽣活的体现。
知识点⼆:中⼼对称图形和中⼼对称1.在平⾯内,⼀个图形绕某个点旋转180°,能与原来的图形重合,这个图形叫做中⼼对称图形,这个点叫做它的对称中⼼,旋转前后图形上能够重合的点叫做对称点.2.在平⾯内,⼀个图形绕某⼀定点旋转180°,它能够与另⼀个图形重合,就说这两个图形关于这个点成中⼼对称,这个点叫做对称中⼼,旋转后两个图形上能够重合的点叫做关于对称中⼼的对称点.3.中⼼对称与中⼼对称图形的区别与联系区别:(1)中⼼对称是指两个图形的位置关系,⽽中⼼对称图形是指具有某种性质的⼀类图形;(2)成中⼼对称的两个图形的对称点分别在两个图形上,⽽中⼼对称图形的对称点在同⼀个图形上.联系:若把中⼼对称图形的两部分看成两个图形,则它们成中⼼对称;若把成中⼼对称的两个图形看成⼀个整体,则成为中⼼对称图形.重点:正确认识中⼼对称。
难点:正确区分中⼼对称与轴对称图形。

中考数学知识点总结中考数学《轴对称》知识点:轴对称基本知识中考数学知识点总结|中考数学《轴对称》知识点:轴对称基本知识中学数学考试中的“轴对称”知识点:轴对称基本知识轴对称的定义:沿着直线折叠一个人物。
如果它能与另一个图形重合,则称这两个图形围绕直线对称。
这条直线叫做对称轴。
折叠后的重合点是对应点,称为对称点。
轴对称图形和轴对称图形的特征相同,且从对应点到对称轴的距离相等。
轴对称的性质:(1)与对应点相连的线段被对称轴垂直平分;(2)对应线段相等,对应角相等;(3)关于一条直线对称的两个图形是全等图形。
轴对称的判定:如果两个图形对应点的连接线被同一条直线垂直平分,则两个图形围绕该直线对称。
这样就得到了以下性质:1.如果两个图形围绕一条直线对称,则对称轴是由任何一对对应点连接的线段的垂直平分线。
2.类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
3.线段垂直平分线上的点与线段的两个端点之间的距离相等。
4.对称轴是到线段两端距离相等的点的集合。
轴对称作用:可以通过对称轴的一边从而画出另一边。
通过画对称轴得到的两个图形是全等的。
扩展到轴对称的应用以及函数图像的意义。
轴对称的应用:关于平面直角坐标系的x,y对称意义如果点a和点B围绕坐标系中的直线X对称,则点a的横坐标保持不变,纵坐标为相反的数字。
相反的,如果有两点关于直线y对称,那么点a的横坐标为相反数,纵坐标不变。
关于二次函数像的对称轴公式(又称轴对称公式)设二次函数的解析式是y=ax2+bx+c那么二次函数的对称轴是一条直线x=-B/2a,顶点的横坐标是-B/2a,顶点的纵坐标是(4ac-b2)/4A在几何证题、解题时,如果是轴对称图形,则经常要添设对称轴以便充分利用轴对称图形的性质。
例如,等腰三角形通常会添加顶点角度的平分线;矩形和等腰梯形问题经常添设对边中点连线和两底中点连线;正方形和菱形问题通常会添加对角线等。
另外,如果遇到的图形不是轴对称图形,则常选择某直线为对称轴,补添为轴对称图形,或者通过折叠将轴一侧的图形反射到另一侧,从而实现条件的相对集中。

中考数学轴对称的知识点
中考数学轴对称的知识点
轴对称定义:
把一个图形沿某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线轴对称,这条直线就是它的对称轴。
折叠后重合的点叫对称点。
轴对称图形:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫轴对称图形,这条直线就是它的对称轴轴对称的性质:
①轴对称的两个图形是全等图形;轴对称图形的两个部分也是全等图形。
②轴对称(轴对称图形)对应线段相等,对应角相等。
③如果两个图形成轴对称,那么对称轴是任何一对对应点所连线段的垂直平分线。
④轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线。
⑤两个图形关于某条直线对称,那么如果它们的.对应线段或延长线相交,那么交点一定在在对称轴上。
常见图形的对称轴:
①线段有两条对称轴,是这条线段的垂直平分线和线段所在的直线。
②角有一条对称轴,是角平分线所在的直线。
③等腰三角形有一条对称轴,是顶角平分线所在的直线。
④等边三角形有三条对称轴,分别是三个顶角平分线所在的直线。
⑤矩形有两条对称轴,是相邻两边的垂直平分线。
⑥正方形有四条对称轴,是相邻两边的垂直平分线和对角线所在的直线。
⑦菱形有两条对称轴,是对角线所在的直线。
⑧等腰梯形有一条对称轴,是两底垂直平分线。
⑨正多边形有与边数相同条的对称轴。
⑩圆有无数条对称轴,是任何一条直径所在的直线。
对称轴的画法:
①找出一对对称点②连对称点线段
③做出对称点所连线段的垂直平分线。

2016中考数学必考轴对称与轴对称图形_考点解析
【摘要】查字典数学网为各位考生整理了2016中考数学必考轴对称与轴对称图形,希望可以帮考生一臂之力。
1.轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,两个图形中的对应点叫做对称点,对应线段叫做对称线段。
2.轴对称图形:如果一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
注意:对称轴是直线而不是线段
3.轴对称的性质:
(1)关于某条直线对称的两个图形是全等形;
(2)如果两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线;
(3)两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上;
(4)如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
中考数学知识点归纳:轴对称一、轴对称与轴对称图形:1.轴对称:把一个图形沿着某一条直线折叠,假如它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,两个图形中的对应点叫做对称点,对应线段叫做对称线段。
2.轴对称图形:假如一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,那么那个图形叫做轴对称图形,这条直线确实是它的对称轴。
注意:对称轴是直线而不是线段3.轴对称的性质:(1)关于某条直线对称的两个图形是全等形;(2)假如两个图形关于某条直线对称,那么对称轴是对应点连线的垂直平分线;(3)两个图形关于某条直线对称,假如它们的对应线段或延长线相交,那么交点在对称轴上;(4)假如两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
4.线段垂直平分线:(1)定义:垂直平分一条线段的直线是这条线的垂直平分线。
那个工作可让学生分组负责收集整理,登在小黑板上,每周一换。
要求学生抽空抄录同时阅读成诵。
其目的在于扩大学生的知识面,引导学生关注社会,热爱生活,因此内容要尽量广泛一些,能够分为人一辈子、价值、理想、学习、成长、责任、友谊、爱心、探究、环保等多方面。
如此下去,除假期外,一年便能够积存40多则材料。
假如学生的脑海里有了众多的鲜活生动的材料,写起文章来还用乱翻参考书吗?(2)性质:①线段垂直平分线上的点到这条线段两个端点的距离相等;②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
教师范读的是阅读教学中不可缺少的部分,我常采纳范读,让幼儿学习、仿照。
如领读,我读一句,让幼儿读一句,边读边记;第二通读,我大声读,我大声读,幼儿小声读,边学边仿;第三赏读,我借用录好配朗读磁带,一边放录音,一边幼儿反复倾听,在反复倾听中体验、品味。
注意:依照线段垂直平分线的这一特性能够推出:三角形三边的垂直平分线交于一点,同时这一点到三个顶点的距离相等。
课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也专门难做到恰如其分。
中考数学轴对称知识点总结一、轴对称的基本概念1.定义:平面上有一条直线l,如果平面上的任意一点A关于这条直线l对称的点A'仍在平面上,那么,点A和点A'就是轴对称的。
2.轴对称轴:直线l二、轴对称的性质1.对称性:图形关于对称轴对称2.对称图形的性质:对称图形的性质有对称图形的性质有点的对称性,直线的对称性和图形的对称性(1)对称图形的重要性质之一是:对称图形的对应点关于对称轴的距离相等,即在同一个垂直于对称轴的直线上。
(2)对称图形的关于对称轴对称的图形有相等的面积(3)对称图形的关于对称轴对称的图形有相等的周长(4)对称图形的对称轴上的点是对称图形的特殊点,其特点就是对称点是对称图形的重要性质之一。
(5)对称图形的两点关于对称轴的坐标值成等差数列(6)对称图形的两点关于对称轴的距离等于这两个点的距离与对称轴的距离的差的绝对值。
三、轴对称的作图1.作法一:通过纸折法:将一角落对着另一个角落折叠,如图1所示,然后用笔在折线上贴上点,最后将纸展开,在对称轴处连结这些点,就得到了折线对称的形状。
2.作法二:通过线段在对称轴的投影:将要对称的形状隔绝一个水平的或垂直的对称轴,如图2所示,然后将这个形状通过容器等物体描绘再一对对称轴的一边,然后再将这个形状在对称轴的投影到对称轴另一边,最后形状保持不变。
最终得到了线段的对称形状。
四、轴对称的应用1.轴对称在几何中的应用:轴对称在几何中被广泛应用,比如用轴对称的性质证明图形的对称性、图形的面积和周长、构造图形等。
2.轴对称在日常生活中的应用:轴对称在日常生活中有许多应用,如我们在家里摆设摆件、铺地砖、装饰墙壁等都需要用到轴对称的知识。
五、轴对称的相关知识1.轴对称的判断:如果图形关于一条直线对称,那么这条直线就是对称轴,如图中所示的三角形ABC绕着O轴对称成了三角形A'B'C'。
2.轴对称的问题:轴对称的问题通常是指图形相对于轴线的位置,或者轴线的位置相对于图形的位置。
轴对称知识点总结1、轴对称图形:一个图形沿一条直线对折,直线两旁的部分能够完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
2、轴对称:两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。
这条直线叫做对称轴。
互相重合的点叫做对应点。
3、轴对称图形与轴对称的区别与联系:(1)区别。
轴对称图形讨论的是“一个图形与一条直线的对称关系” ;轴对称讨论的是“两个图形与一条直线的对称关系”。
(2)联系。
把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称;把轴对称的“两个图形看作一个整体”便是轴对称图形。
4、轴对称的性质:(1)成轴对称的两个图形全等。
(2)对称轴与连结“对应点的线段”垂直。
(3)对应点到对称轴的距离相等。
(4)对应点的连线互相平行。
5、线段的垂直平分线:(1)定义。
经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。
如图2,∵CA=CB ,直线m ⊥AB 于C , ∴直线m 是线段AB 的垂直平分线。
(2)性质。
线段垂直平分线上的点与线段两端点的距离相等。
如图3,∵CA=CB ,直线m ⊥AB 于C ,点P 是直线m 上的点。
∴PA=PB 。
(3)判定。
与线段两端点距离相等的点在线段的垂直平分线上。
如图3,∵PA=PB ,直线m 是线段AB 的垂直平分线,∴点P 在直线m 上 。
6、等腰三角形:(1)定义。
有两条边相等的三角形,叫做等腰三角形。
相等的两条边叫做腰。
m C A B 图1图2m C A B P 图3 顶第三条边叫做底。
②两腰的夹角叫做顶角。
③腰与底的夹角叫做底角。
说明:顶角=180°- 2底角底角=顶角顶角21-902180︒=-︒ 可见,底角只能是锐角。
(2)性质。
①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线” ,只有一条。
②等边对等角。
如图5,在△ABC 中∵AB=AC∴∠B=∠C 。
③三线合一。
(3)判定。
①有两条边相等的三角形是等腰三角形。
初中数学轴对称知识点总结归纳轴对称是几何学中的一个重要概念,关于轴对称的知识在初中数学中有着广泛的应用。
下面是初中数学轴对称的知识点总结归纳。
一、轴对称的定义及性质轴对称即物体围绕条线旋转180度后仍然与原来位置重合。
1.定义:轴对称是指平面内的点、线、图形等围绕条线旋转180度后仍然与原来位置重合。
2.性质:a.旋转中心即轴对称的轴上的任意点保持不动。
b.旋转中心与轴对称的物体上的任意点之间的距离保持不变。
二、轴对称的判断判断一个图形是否轴对称的方法有以下几种:1.观察法:观察图形是否看起来关于条线对称。
2.折叠法:将图形沿着条疑似对称轴对折,观察是否能够将两部分完全重合。
3.旋转法:将图形围绕一个疑似对称轴旋转180度,观察是否与原来位置完全重合。
4.对称性质法:观察图形是否具有对称性质,例如左右对称、上下对称等。
三、轴对称的应用1.确定轴对称图形:a.线段的中点是线段轴对称的轴。
b.两个且只有两个端点在同一直线上的线段是轴对称的轴。
c.两条平行线是轴对称的轴。
d.三个且只有三个顶点都在同一直线上的三角形是轴对称的轴。
e.按顺时针方向给出的相邻边相等的凸多边形是轴对称的轴。
f.所有与自己相似的图形都是轴对称的轴。
2.轴对称图形的性质:a.轴对称图形是左右对称的,即图形的左半部分和右半部分完全一样。
b.轴对称图形的最小单位即轴上的点称为轴对称图形的旋转中心。
c.轴对称图形的每个点的两边都有另一个对称点。
d.轴对称图形上的点与旋转中心距离相等的点是该图形上的点与旋转中心的对称点。
3.构造轴对称图形:a.已知轴对称图形的一部分,可以使用对称性质构造其他部分。
b.可以将点在轴上折叠,或者将线段、角度在轴上旋转,得到图形的对称部分。
四、轴对称图形的操作1.旋转:将轴对称的物体沿着轴旋转180度,使得物体的每个点都与轴上的对称点相重合。
2.平移:将轴对称的物体沿着与轴垂直的平行线平移,使得物体与原来位置的对称关系保持不变。
考点三十二:图形的轴对称聚焦考点☆温习理解1.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点.2.图形轴对称的性质如果两个图形关于某条直线对称,那么对称轴是任意一对对应点所连线段的垂直平分线.轴对称图形的对称轴,是任意一对对应点所连线段的垂直平分线.对应线段、对应角相等.3.由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全一样;新图形上的每一点,都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.这样,由一个平面图形得到它的轴对称图形叫做轴对称变换.一个轴对称图形可以看作以它的一部分为基础,经轴对称变换而成.4. 轴对称与轴对称图形轴对称图形和图形的轴对称之间的的区别是:轴对称图形是一个具有特殊性质的图形,而图形的轴对称是说两个图形之间的位置关系;两者之间的联系是:若把轴对称的两个图形视为一个整体,则它就是一个轴对称图形;若把轴对称图形在对称轴两旁的部分视为两个图形,则这两个图形就形成轴对称的位置关系.名师点睛☆典例分类考点典例一、识别轴对称图形【例1】(2015绵阳)下列图案中,轴对称图形是()A. B. C. D.【答案】D.考点:轴对称图形.【点睛】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.判断图形是否是轴对称图形,关键是理解、应用轴对称图形的定义,看是否能找到至少1条合适的直线,使该图形沿着这条直线对折后,两旁能够完全重合.若能找到,则是轴对称图形;若找不到,则不是轴对称图形.【举一反三】1.(2015.山东日照,第1题,3分)下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是()A. B. C. D.【答案】D考点:轴对称图形.2.(2015.天津市,第3题,3分)在一些美术字中,有的汉字是轴对称图形,下面4个汉字中,可以看作是轴对称图形的是( )吉祥如意(A)(B)(C)(D)【答案】A.【解析】试题分析:根据轴对称图形的概念,在一个平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;四个选项中只有选项A符合要求,故答案选A.考点:轴对称图形的概念.考点典例二、作已知图形的轴对称图形【例2】(2014•厦门)在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.【答案】考点:作图-轴对称变看完换.【点睛】此题主要考查了轴对称变换,得出对应点坐标是解题关键.画轴对称图形,关键是先作出一条对称轴,对于直线、线段、多边形等特殊图形,一般只要作出直线上的任意两点、线段端点、多边形的顶点等的对称点,就能准确作出图形.【举一反三】在4×3的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).(1)是轴对称图形,又是中心对称图形;(2)是轴对称图形,但不是中心对称图形;(3)是中心对称图形,但不是轴对称图形.【答案】作图见解析.【解析】试题分析:(1)可组成长方形;(2)可组成楼梯形状;(3)可组成平行四边形.试题解析:画图如下:考点:利用旋转设计图案;利用轴对称设计图案.考点典例三、轴对称性质的应用【例3】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是【答案】5.【解析】试题分析:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.试题解析:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,∵四边形ABCD是菱形,∴AC⊥BD,∠QBP=∠MBP,即Q在AB上,∵MQ⊥BD,∴AC∥MQ,∵M为BC中点,∴Q为AB中点,∵N为CD中点,四边形ABCD是菱形,∴BQ∥CD,BQ=CN,∴四边形BQNC是平行四边形,∴NQ=BC,∵四边形ABCD是菱形,∴CP=12AC=3,BP=12BD=4,在Rt△BPC中,由勾股定理得:BC=5,即NQ=5,∴MP+NP=QP+NP=QN=5.考点:轴对称-最短路线问题;勾股定理的应用;平行四边形的判定与性质;菱形的性质.【点睛】求两条线段之和为最小,可以利用轴对称变换,使之变为求两点之间的线段,因为线段间的距离最短.本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.【举一反三】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.1.【解析】试题分析:根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.试题解析如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,过点M 作MF ⊥DC 于点F ,∵在边长为2的菱形ABCD 中,∠A=60°,M 为AD 中点, ∴2MD=AD=CD=2,∠FDM=60°, ∴∠FMD=30°, ∴FD=12MD=12,∴FM=DM ×cos30°=2,∴∴A ′C=MC-MA ′1.考点:菱形的性质;翻折变换(折叠问题). 考点典例四、折叠问题【例4】(2015.宁夏,第14题,3分)如图,在矩形ABCD 中,AB =3,BC =5,在CD 上任取一点E ,连接BE ,将△BCE 沿BE 折叠,使点E 恰好落在AD 边上的点F 处,则CE 的长为 .【答案】35.考点:矩形的性质;折叠的性质;勾股定理.【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.折叠的过程实际上就是一个轴对称变换的过程,轴对称变换前后的图形是全等图形,对应边相等,对应角相等.【举一反三】1.如图,将矩形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF=【答案】45°.考点:角的计算;翻折变换(折叠问题).2.(2015·黑龙江绥化)在矩形ABCD中,AB=4 , BC=3 , 点P在AB上。
若将△DAP沿DP折叠,使点A 落在矩形对角线上的A 处,则AP的长为__________.【答案】32或94【解析】试题分析:分两种情况讨论:①点A落在矩形对角线BD上,如图1,∵AB=4,BC=3,∴BD=5,根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,∴BA′=2,设AP=x,则BP=4-x,∵BP2=BA′2+PA′2,∴(4-x)2=x2+22,解得:x=32,∴AP=32;②点A落在矩形对角线AC上,如图2,根据折叠的性质可知DP⊥AC,∴△DAP∽△ABC,∴AD AB AP BC=,∴AP=•AD BCAB=334=94.故答案为:32或94考点:1.矩形的折叠;2.直角三角形的性质;3.相似三角形的判定与性质.课时作业☆能力提升一、选择题1. (2015.北京市,第4题,3分)剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为()A. B. C. D.【答案】D.【解析】试题分析:在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,则这个图形叫轴对称图形;D符合轴对称图形的定义,故选D.考点:轴对称图形2. (2015成都)如图,在平行四边形ABCD中,AB AD=4,将平行四边形ABCD沿AE翻折后,点B 恰好与点C重合,则折痕AE的长为________.【答案】3.考点:1.翻折变换(折叠问题);2.勾股定理;3.平行四边形的性质.3.(2015达州)如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为.【答案】94.【解析】考点:1.翻折变换(折叠问题);2.综合题.4.(2015内江)如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为.考点:1.翻折变换(折叠问题);2.综合题.5.(2015凉山州)菱形ABCD 在平面直角坐标系中的位置如图所示,顶点B (2,0),∠DOB=60°,点P 是对角线OC 上一个动点,E (0,﹣1),当EP+BP 最短时,点P 的坐标为 .【答案】(3,2.【解析】试题分析:连接ED ,如图,∵点B 的对称点是点D ,∴DP=BP ,∴ED 即为EP+BP 最短,∵四边形ABCD 是菱形,顶点B (2,0),∠DOB=60°,∴点D 的坐标为(1,∴点C 的坐标为(3,∴可得直线OC的解析式为:3y x =,∵点E 的坐标为(﹣1,0),∴可得直线ED的解析式为:(11y x =-,∵点P 是直线OC 和直线ED 的交点,∴点P的坐标为方程组(11y x y x ⎧=⎪⎨⎪=+-⎩的解,解方程组得:32x y ⎧=⎪⎨=⎪⎩,所以点P 的坐标为(3,2),故答案为:(3,2.考点:1.菱形的性质;2.坐标与图形性质;3.轴对称-最短路线问题;4.动点型;5.压轴题;6.综合题.6.如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5 cm,PN=3 cm,MN=4 cm,则线段QR的长为( )A.4.5 cm B.5.5 cm C.6.5 cm D.7【答案】A.考点:轴对称的性质.7. (2014•德州)如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD 沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,以上结论中,你认为正确的有()个.A.1 B.2 C.3 D.4【答案】C.试题解析:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,∴FH∥CG,EH∥CF,∴四边形CFHE是平行四边形,由翻折的性质得,CF=FH,∴四边形CFHE是菱形,(故①正确);∴∠BCH=∠ECH,∴只有∠DCE=30°时EC平分∠DCH,(故②错误);点H与点A重合时,设BF=x,则AF=FC=8-x,在Rt△ABF中,AB2+BF2=AF2,即42+x2=(8-x)2,解得x=3,点G与点D重合时,CF=CD=4,∴BF=4,∴线段BF的取值范围为3≤BF≤4,(故③正确);过点F作FM⊥AD于M,则ME=(8-3)-3=2,由勾股定理得,==综上所述,结论正确的有①③④共3个.故选C.考点:翻折变换(折叠问题);勾股定理的应用;菱形的判定与性质.二、填空题8.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折叠,使点B恰好落在边AC上,与点B′重合,AE为折痕,则EB′=____【答案】1.5.【解析】试题分析:首先根据折叠可得BE=EB′,AB′=AB=3,然后设BE=EB′=x,则EC=4-x,在Rt△ABC中,由勾股定理求得AC的值,再在Rt△B′EC中,由勾股定理可得方程x2+22=(4-x)2,再解方程即可算出答案.试题解析:根据折叠可得BE=EB′,AB′=AB=3,设BE=EB′=x,则EC=4-x,∵∠B=90°,AB=3,BC=4,=,∴在Rt△ABC中,由勾股定理得,5∴B′C=5-3=2,在Rt△B′EC中,由勾股定理得,x2+22=(4-x)2,解得x=1.5.考点:翻折变换(折叠问题).9.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有____种.【答案】3.考点:利用轴对称设计图案.10. (2015攀枝花)如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为.考点:1.轴对称-最短路线问题;2.等边三角形的性质;3.最值问题;4.综合题.11.(2015·黑龙江绥化)如图 ,在矩形ABCD 中 ,AB=10 , BC=5 . 若点M 、N 分别是线段ACAB 上的两个动点 ,则BM+MN 的最小值为( ) A. 10 B. 8 C. 53 D. 6【答案】B【解析】试题分析:作点B 关于AC 的对称点E ,过E 作EF 垂直AB 交AB 于F 点,此时BM+MN 的值最小=EF 的长,由勾股定理可得:=S △ABC =12AC •BQ=12AB •BC ,∴AC 边上的高=BE=2BQ=∵∠ABQ=∠EBF ,∠AQB=∠EFB=90°,∴△BEF ∽△BAQ , ∵△BAQ ∽△CAB ,∵△CAB ∽△BEF ,∴AB AC EF BE =,即10EF =∴EF=8,故选:B .考点:1.矩形的性质;2.轴对称;3.相似三角形的判定与性质.三、解答题1.(2015乐山)(10分)如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC 于点E.(1)求证:△DCE≌△BFE;(2)若CD=2,∠ADB=30°,求BE的长.【答案】(1)证明见试题解析;(2.试题解析:(1)∵AD∥BC,∴∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,∴∠DBC=∠BDF,∴BE=DE,在△DCE和△BFE中,∵∠BEF=∠DEC,∠F=∠C,BE=DE,∴△DCE≌△BFE;(2)在Rt △BCD 中,∵CD=2,∠ADB=∠DBC=30°,∴BC=Rt △BCD 中,∵CD=2,∠EDC=30°,∴DE=2EC ,∴222(2)EC EC CD -=,∴,∴BE=BC ﹣考点:1.翻折变换(折叠问题);2.全等三角形的判定与性质.。