怎样不用尺子只用圆规把圆分成4等分

正方形四等分的方法可以参考以下几种：
1. 利用勾股定理法：正方形四等分的一个好方法就是利用勾股定理，即通过找到正方形的三个直角来等分。

你可以先在纸上画一个正方形，再画出三条互相垂直的直线，将正方形分成四份。

这种方法充分利用了直角三角形的特性，是一个简单但有效的方法。

2. 利用折纸法：将正方形对角线折叠，然后再对折剩下的半正方形，此时，就可以将原来的正方形四等分。

这种方法可以直观地看到四等分的成果，有助于理解和验证。

3. 利用尺子和圆规法：使用尺子和圆规将正方形分割成四等份。

首先在正方形的四个顶点分别画一个圆，然后使用圆规将每个顶点分割成四份，就完成了四等分。

4. 使用模板法：可以制作一个模板，将其贴在正方形的四个角上，用剪刀或者刀子进行切割，就可以得到四个等份。

这种方法需要制作模板，可能需要一些技巧和经验。

这些方法都有各自的优点和适用性，可以根据实际情况选择合适的方法来进行四等分。

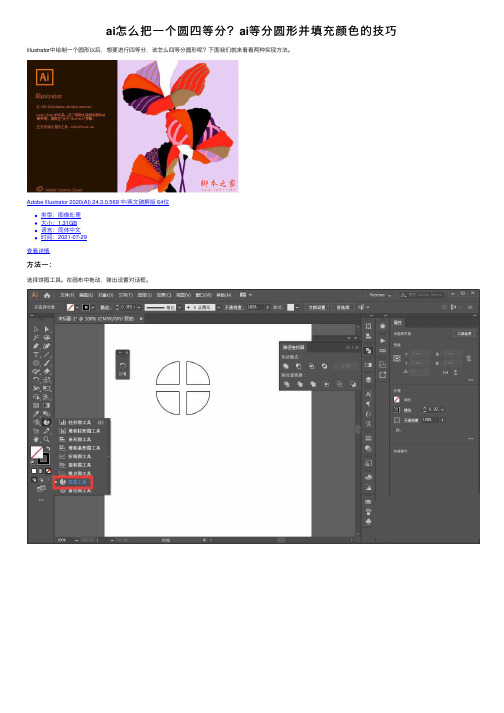
ai怎么把⼀个圆四等分？ai等分圆形并填充颜⾊的技巧illustrator中绘制⼀个圆形以后，想要进⾏四等分，该怎么四等分圆形呢？下⾯我们就来看看两种实现⽅法。

Adobe Illustrator 2020(AI) 24.3.0.569 中/英⽂破解版 64位
类型：图像处理
⼤⼩：1.31GB
语⾔：简体中⽂
时间：2021-07-29
查看详情
⽅法⼀：
选择饼图⼯具。

在画布中拖动，弹出设置对话框。

填⼊4个相同的数字。

点应⽤按钮。

在菜单栏点对象-取消编组。

弹出提⽰对话框，点确定按钮。

四等分的圆就做好了。

⽅法⼆：
打开illustrator，新建⼀个⽂档。

使⽤椭圆⼯具，快捷键L。

按住shift绘制⼀个正圆。

使⽤直线⼯具，快捷键\。

按住shift绘制⽔平和垂直的直线。

打开对齐⾯板，快捷键shift+F7。

选中圆和直线，⽔平垂直居中对齐。

打开路径查找器⾯板，快捷键ctrl+shift+f9，点分割按钮。

右键-取消编组。

圆就被四等分了。

以上就是ai等分圆形并填充颜⾊的技巧，希望⼤家喜欢，请继续关注。

圆分等分的计算公式
咱们今天来聊聊圆分等分的那些事儿。

比如说，我们想把一个圆分成4份。

那这个时候呀，整个圆是360度，我们用360度除以4，就得到了每一份是90度。

这就像把一个大圆盘蛋糕切成了4块，每一块的角都是90度呢。

想象一下，这个90度的角，就像我们直角三角板的那个直角一样直直的。

再举个例子，如果我们要把圆分成6份。

那还是用360度除以6，这样算出来每一份就是60度。

你可以拿一张圆形的纸，试着把它像这样分成6份。

你会发现每一份的角度都是60度，就像小扇子一样。

这6份合起来又能拼成一个完整的圆，多有趣呀。

那要是我们想把圆分成8份呢？按照公式，360度除以8等于45度。

这就像把一个超级大的披萨分成了8块，每一块的角就是45度。

我再给你们讲个小故事吧。

有一次，学校里做手工活动，要做一个有很多等分的圆形装饰。

小明不知道怎么才能把圆平均分好，急得满头大汗。

这时候，小红告诉他这个圆分等分的小秘密，就是用360度除以要分的份数。

小明按照这个方法，很轻松地就把圆分成了他想要的份数，做出了超级漂亮的圆形装饰。

还有那种有很多扇叶的风扇，它的扇叶也是把圆给等分了。

如果是3个扇叶，那就是把圆分成3份，每一份是360度除以3等于120度。

从“四等分圆面积”说起厦门市教育局 任 勇思维是人类特有的一种精神活动。

孔子说“学而不思则罔”，意思是说“只读书而不思考，就等于没有读书”。

发散思维，即求异思维，是从一到多的思维，它往往是从一个问题、一个条件、一个已知事项出发，沿着不同同的方向，从不同的角度，取寻求不同的答案。

其特殊，表现为思维活动的多向性；其功能，表现为可不断挖掘深层信息，创新思路和方法；其操作，表现为由点到线，由线到网，由网到体的思维境界。

由人说，发散思维是“思维与灵魂的对话”，也有人说，发散思维训练，可以让人深深体味到“纸上得来终觉浅，心中悟出方知深”得真谛。

发散思维训练，有许多方法和典型例题，就数学而言，我觉得“四等分圆面积”问题，就是一个很好得“题根”。

问题：将一个半径为r 的圆分成四个面积相等的部分，请尽可能多地设计分割方法，并分析那些方法可以用尺子和圆规作出。

我们相信，图1是全班同学都会向到的分割方法。

图2和图3的分割方法也不是很难想到的。

图1 图2 图3哲学家哥德曾风趣地说：“经验丰富的人读书用两只眼睛，一只眼睛看到纸的花，另一只眼睛看到纸的背面。

”教师要引导学生找规律、抓本质，揭示图1、2、3实质是：由圆心O 与圆周上一点P “任意连线”，将连线连续三次向同一方向旋转90度，即“一般性地解决了这类问题”，再见图4，特别说明，这条“连线”可以是曲线，只要这条曲线尺规能作出，则可以由尺规分割。

这种分割法，其实可以作出无数种。

图4 图5 图6但，上述方法仍无突破“全等”的情形。

能否突破“全等”的情形，分割成“不全等”的情形呢？ 我相信，学生一定能发现，半径为2r 的圆的面积是原来圆面积的14沿着这条线索，可得到图5，图6。

教师此时要给学生“极大的鼓励”，因为他有突破。

还能沿着这思维再挖一点吗？学生跃跃欲试，全班突然安静下来，突然，有个学生叫道“我有了”。

图7 图8 图9图7的构造令我惊愕！，也令全班同学惊愕！继而全班同学情不自禁地鼓掌，这是“对他智慧的最高赞赏”，从而让学生体会到了“探索的快乐”和“成功的快乐”。

圆分十二等分的最简单方法圆是一种通用的几何形状，被广泛应用在艺术、美学和工程等多个学科之中，并有着深远的文化含义。

圆的完美美感和协调统一的特性受到了众多设计师的青睐，比如印刷媒介中的徽标、海报、广告以及网页设计等，均多以圆形为主，以达到艺术效果。

这就提出了一个关于圆分割的技术问题，即如何将一个圆分割成十二等分，而且尽可能的使用简单的操作。

其实，把一个圆分割成十二等分的最简单方法是用刻度尺，但若要将圆分割成十二等分，就需要用到分针原理，这是一种有效的几何绘图方法，可以将一个圆分割成多个等份，例如两等份、四等份、六等份、十二等份等。

顾名思义，这种方法依赖于分针原理，把圆分割成多等份，每份之间的角度都是相同的。

首先，在圆上划出四等分，可以用尺子直接标记出四个点，即圆的起点、中点、终点和一半的圆周点，并连接这四个点，把圆分割成了四等份。

接下来，再把每一等份再分割成三等份，可以利用两个线段在每一个等份中各画出一条分割线，把一个等份分成两部分，这样就把圆分割成了十二等份了。

除此之外，利用三角函数求解，也可以快速地将一个圆分割成十二等份：首先将圆心设置为原点，用极坐标表示，则可以得到它的坐标为（r、），其中，r 为圆的半径，θ与圆心连线与圆上任一一点连线所成夹角，以弧度为单位，这就是极坐标系。

据此，可以得出十二等份的坐标：（r、2π/12），（r、4π/12），（r、6π/12），（r、8π/12），（r、10π/12），（r、 12π/12）。

把这六组坐标换算成直角坐标，即可以得出它们在圆上的坐标。

以上就是把一个圆分割成十二等份的最简单方法，它们可以满足各种应用需求，比如搭建艺术性的设计图案，也可以用于测量和观察地球表面，例如汽车零部件组装等工业应用。

圆的几何性质使它的分割能够满足各种应用的需求，其中分等分的最简单方法和最有效的方法都有所不同，但它们都是相当重要的，在几何图形的研究与应用中更是如此。

总之，分针原理和三角函数求解是把一个圆分割成十二等份的最简单方法，它们可以让把一个圆分割成十二等份变得更加容易，而且准确度也更高，可以为不同的绘图和设计应用提供有效的支持。

cad等分圆周的方法在数学中，将一个圆的圆周分成多个等分的方法被称为“等分圆周”。

等分圆周是进行各种几何和三角学问题计算的基础，因此有许多方法可以用来等分圆周。

下面将介绍几种常用的等分圆周方法。

1.平分圆周：平分圆周是将圆周分成相等的n份。

最简单的方法是使用直尺和细线，将直径和圆周连起来，然后将细线按照需要的份数分开。

也可以利用圆规和直尺的方法：将圆规的一只脚放在圆心，另一只脚放在圆周上，然后画弧，重复这个过程，直到得到所需的份数。

2.利用正多边形：正多边形是指所有边和角相等的多边形。

将一个圆周等分成n份的方法之一是利用正n边形。

首先，以圆心为中心，画一个半径为r的大圆。

然后，根据正n边形的定义，将大圆分成n个相等的扇形。

最后，通过连接相邻的扇形的边，得到一个正n边形。

这样，圆周就被等分成了n份。

3.利用圆心角：圆心角是指以圆心为顶点的角。

将一个圆周等分成n份的方法之一是利用圆心角。

首先，以圆心为中心，画一个半径为r的大圆。

然后，根据圆心角的定义，将大圆分成n个相等的圆心角。

最后，在每个圆心角的两条射线上划分相同长度的弧，得到n个等分的圆周。

4.利用三等分角：三等分角是指将一个角分成三个相等的角。

将一个圆周等分成三等分的方法之一是利用三等分角。

首先，以圆心为中心，画一个半径为r的大圆。

然后，找到任意一条半径，将其在圆周上分成三等分的点，再通过这些点连接圆心，得到三等分角的射线。

最后，在每个射线上划分相同长度的弧，得到三个等分的圆周。

5.利用复杂图形：除了以上提到的方法，还可以利用复杂图形等分圆周。

例如，在圆周上画一个正五边形，然后通过将五个顶点连接到圆心，将圆周等分成五份。

同样的方法也适用于其他复杂图形，例如正六边形、正七边形等。

以上是几种常用的等分圆周方法，每种方法都有其适用的场合。

根据具体的问题和要求，可以选择其中的一种或多种方法进行等分圆周。

这些方法都遵循数学准则，通过合理的构造和计算，能够准确地等分圆周，为解决各种几何和三角学问题提供了基础。

第三十八届中小学科学展览会作品说明书封面科别：数学科组别：国中组作品名称：无尺之图－只用圆规的作图关键词：圆规作图、compass alone编号：无尺之图—只用圆规的作图摘要：数学课本在标尺作图之后，提到了拿破仑用圆规四等分圆周，老师又说标尺作图可以作的事，圆规作图也可以作出来。

我实在非常惊讶所以便开始进行圆规作图的研究。

我先将搜集到的资料中已经研究过的圆规作图，依序模拟研究一遍，并加以证明。

再将平常标尺作图的一些图，只用圆规在绘图软件GSP上作图。

借着实际作图，我验证了圆规作图的可行性。

不过也体会圆规作图的复杂，所以每次挑战出一种图形之后，实在太有成就感！整个研究提升了我的几何功力，这是我最大的收获。

壹、研究动机：康轩课本二下介绍完标尺作图之后，有一页提到拿破仑只用圆规将一给定圆的圆周四等分，他的作法非常特别，吸引了我们的兴趣。

加上老师又说数学家已经研究出标尺作图可以作的事，圆规作图也可以作出来。

我们实在非常惊讶所以便开始进行圆规作图的研究。

貳、研究目的：将我们课程中常作的标尺作图，不用尺只用圆规作出来！(若结果为一直线，则只须找出此直线上的任意两点即可)參、研究器材：圆规、笔、纸、Cabri(展示用软件)、GSP(书面报告绘图用软件)、一颗清楚的头脑我们先将资料中已经研究过的圆规作图，依以下顺序仿真研究一遍：一、等线段作图二、对称点作图三、垂直作图四、平行四边形作图五、反演点作图六、等分线段作图七、第四比例项作图八、弧中点作图九、圆与直线交点作图十、两直线交点作图上列的十项作图法，已经完成所有标尺作图可以做到的图，接着我们研究课程中常做的作图：十一、找在线其他点十二、找圆心十三、作垂足十四、作角平分线十五、作正方形十六、作垂心十七、作重心十八、作内心十九、作外心二十、作五边形二十一、作九点圆我们先订定A(BC)为以A为圆心，BC为半径的圆。

一、给定A,B两点，做出AB的任意整数倍。

(一)方法：做B(AB)和A(AB)交于一点C做B(AB)和C(BC)交于一点D做B(AB)和D(BD)交于一点E则AE=2AB将B当做原A，E当做原B，则可做出AB的任意整数倍。

拿破仑的四等分圆问题拿破仑虽然是位军事家，但他与当时的许多法国知名数学家，如拉格朗日，拉普拉斯等交往都颇密切，一次拿破仑问拉普拉斯：“我读了您不少的大作，我对您在您的书中竟然一次都不提上帝很不理解，您能解释一下吗？”拉普拉斯不客气地回答：“陛下，我不需要那个假设。

”对拉普拉斯的傲慢态度，拿破仑却并未发火，仍给了他很多的荣誉与职位，从这一点看，拿破仑倒颇有一点“尊重知识，尊重人材”的大将风度。

拿破仑尽管忙于打仗，但仍经常与数学家们讨论数学，有一次，拿破仑就提出这样一个问题：“给出一个圆，只准用圆规，把圆周四等分”。

大家知道，几何作图题是规定只准使用圆规与无刻度的直尺来完成的，这两种工具的功能规定为：（1）已知圆心及半径，用圆规作圆。

（2）已知两点，用直尺作过这两点的直线。

（3）已知两圆，或已知两直线，或已知一圆及一直线，找出它们的交点。

另外还限制只准有限次地使用这两种工具，逐步作出所需图形，如果不准使用直尺，只准使用圆规来完成作图，就是“圆规几何学”的内容，或称为“单用圆规的作图问题”。

如果补充规定用圆规“画直线”可以理解为：“若已知直线上两点，则可画出直线上任意多个点。

”那么，可以证明：能用圆规与直尺完成的图，都可用圆规单独完成。

例1，作一线段等于已知线段的任意整数倍。

由于圆规很容易把一个（圆心已知的）已知圆6等分，利用这一点即可完成本作图。

如图，已知线段为AB，以B为圆心，BA＝a为半径作圆，以A为一个分点，把圆B六等分，与A相对的分点为C，则AC=2AB。

如此下去，就可以把已知线段延长任意整数值。

例2，把已知线段AB 分成n 等分（n≥2为整数）。

以n ＝3为例，由上题可知，可以作出点C ，使点C 在AB 延长线上且使AC ＝3AB 。

以C 为圆心CA 为半径画圆，再以A 为圆心，AB 为半径画圆，两圆交点之一为D ，以D 为圆心，AB 为半径画圆，交AB 于M ，证明：△ACD、△ADM 均为等腰三角形，且有一个底角公用，于是△ACD∽△ADM，于是AC∶AD=AD∶AM 但AC=3AD ，于是可得AD=3AM 即AM= 31AB 。

万能等分圆
用圆规和直尺把一个圆N 等分，该怎么分呢？先辈们总结了等分圆的很多方法。

针对特殊的等分还总结了不少准确、简便的方法，如圆的3等分 ……
例：3等分圆：用直尺先画一条直径，然后以直径的一端点为圆心、半径为定长，画出与圆周的两交点， 连接两交点以及交点与直径的另一端，即三等分圆。

A B O C
D
在此略过其余等分方法，关键是方法多，时间长，容易忘记。

现在介绍一种圆的万能近似等分方法，常在野外施工、建筑工地、设备安装等精度要求不高行业使用，操作简便，只用圆规和直尺即可。

用万能近似等分法9等分圆：
1. 用直尺画一直线段AB ，根据圆的等分数9（N=9）等分线段，
2. 以AB 的中点O 点为圆心OA 为半径画圆，
3. 以A 点、B 点为圆心AB 为半径画圆交与点P ，
4. 连接P2并延长与点Q ，连接AQ ，以线段AQ 为半径依次等分。

A B
O 2
3
4
5
67
8
9
P
Q
用万能近似等分法3等分圆：
步骤同上： A
B
O
1
23
P
如果已知圆直径，又没有合适的刻度等分直线，可先用圆规二等分直尺，万能近似等分法等分圆，方法如下，
1， 垂直平分（偶数等分）无刻度直尺，依次以直尺的一半（已知线段）画N 条线段，
以线段总长为直径做辅助圆。

2， 以万能近似等分法等分辅助圆，
3， 与已知圆同心后，连接各顶点与圆心，直接相交或延长后相交与已知圆，连接已知
圆各交点即可。