C语言中求最大公约数的两种方法
- 格式:doc
- 大小:26.00 KB
- 文档页数:2

欧几里得算法求最大公约数c语言欧几里得算法是一种用于计算两个整数最大公约数的方法。
也被称为辗转相除法,其算法基于如下等式:gcd(a,b)= gcd(b,a mod b)该等式表示gcd(a,b)等于b和a mod b的最大公约数。
这个过程一直持续到a mod b等于0,此时b就是a和b的最大公约数。
以下是欧几里得算法求最大公约数的c语言实现:```#include <stdio.h>int gcd(int a, int b) {int temp;while (b != 0) {temp = a % b;a = b;b = temp;}return a;}int main() {int num1, num2;printf("请输入两个数:\n");scanf("%d %d", &num1, &num2);printf("最大公约数是 %d", gcd(num1, num2));return 0;}```代码解析:首先,我们定义了一个名为gcd的函数,它接受两个整数a和b,并返回它们的最大公约数。
接下来,我们使用while循环来执行辗转相除法。
我们在每次循环中计算a mod b的值,并将其存储在变量temp中。
之后,我们将b 的值赋给变量a,并将temp的值赋给变量b。
这个过程一直持续到b 等于0,此时a的值就是a和b的最大公约数。
最后,我们在主函数中调用gcd函数,并输出最大公约数。
总结:欧几里得算法是一种非常简单和有效的方法,用于计算两个整数的最大公约数。
该算法用循环来进行计算,并在每次循环中更新变量的值。
在实际编程中,欧几里得算法可以帮助我们优化程序,并节省时间和空间。


关于C语⾔求两个数的最⼤公约数
⼀、求两个数的最⼤公约数有两种⽅法
1、求差法
对于传⼊的两个数,⽤较⼤的数减去较⼩的数,然后拿差与较⼩的数相⽐,若是相等,则这个数就是最⼤公约数。
否则,对于差和较⼩的数再次重复上述的过程。
关于算法,则可利⽤while的循环来重复或者利⽤递归算法,这⾥采⽤递归来求解
1int division(int n,int m)
2 {
3if(n<m)
4 division(m,n); //交换n,m的值
5else if(n==m)
6return n;
7else
8 {
9int temp=n;
10 n=m;
11 m=temp-n;
12 division(n,m); //重复上述过程
13 }
14 }
2、求模法
求模法就是对于传⼊的两个数,⽤较⼤的数来对较⼩的数求模,要是模为零,则较⼤的数则为最⼤公约数。
若是模不为零,则对于较⼩的数和模继续上述的过程。
此过程与上述的求差法⼏乎⼀模⼀样,仍利⽤递归法.
1int division(int n,int m)
2 {
3if(n<m)
4 division(m,n); //交换m与n
5else if(m==0)
6return n;
7else
8 {
9int temp=n;
10 n=m;
11 m=temp%n;
12 division(n,m); //重复上述过程
13 }
14 }
对于最⼩公倍数,则是两数相乘,然后除以最⼤公约数。

c语言求两个数最大公约数,穷举法的时间复杂度C语言求两个数最大公约数,穷举法的时间复杂度在计算机科学领域中,我们经常需要解决各种数学问题,例如求两个数的最大公约数。
而在C语言中,我们可以使用穷举法(也称为暴力法)来求解最大公约数。
在本篇文章中,我们将深入探讨C语言中求两个数最大公约数的问题,并分析穷举法的时间复杂度。
1. 最大公约数的概念最大公约数指的是两个或多个整数共有约数中最大的一个。
在数学上,常用的求最大公约数的方法有辗转相除法、更相减损术和质因数分解法等。
而在计算机科学中,我们可以使用穷举法来求解最大公约数。
下面,我们将以C语言为例,介绍如何使用穷举法来求解两个数的最大公约数。
2. C语言求最大公约数在C语言中,我们可以使用穷举法来求解两个数的最大公约数。
穷举法的基本思路是从较小的数开始,逐渐减小,直到找到两个数的一个公约数为止。
以下是一个简单的C语言程序示例:```c#include <stdio.h>int gcd(int a, int b) {int min = a < b ? a : b;int max = a > b ? a : b;int result = 0;for (int i = 1; i <= min; i++) {if (min % i == 0 && max % i == 0) {result = i;}}return result;}int main() {int a, b;printf("请输入两个整数:");scanf("%d %d", &a, &b);printf("它们的最大公约数是:%d\n", gcd(a, b)); return 0;}```3. 穷举法的时间复杂度穷举法的时间复杂度可以通过一个简单的分析得出。
在上面的C语言程序中,我们使用了一个for循环来进行穷举。

最大公约数c语言最大公约数(GreatestCommonDivisor),也称最大公因数、最大公因子、最大公分子等,是两个或多个数的公约数(公因数),它的绝对值最大。
在数学中,计算最大公约数是非常重要的,也是最基础的计算题。
为了编写程序计算最大公约数,可以使用C语言。
C语言是一种通用计算机编程语言,它具有简单的语法,强大的功能,灵活的控制逻辑。
它是程序员在计算机编程中的必备语言。
下面列出的程序,可以用C语言来计算最大公约数。
首先,我们要定义一些变量,用于保存输入的变量:int m, n; //表示要求最大公约数的两个数int r; //保存最大公约数然后,在程序中读取输入的两个数字:printf (“请输入一组要求最大公约数的两个整数:”);scanf (“%d %d”, &m, &n);接着,我们开始计算最大公约数。
根据辗转相除法,最大公约数等于两个数字的余数。
因此,我们需要使用循环来计算。
while(m != 0 && n != 0){if(m > n){m = m % n;}{n = n % m;}}最后,我们将计算出的最大公约数保存到r变量中:r = m + n;最后,我们可以输出计算得出的最大公约数:printf(“最大公约数为:%d”, r);完整的C语言程序如下:#include <stdio.h>int main(void){int m, n; //表示要求最大公约数的两个数int r; //保存最大公约数printf (“请输入一组要求最大公约数的两个整数:”); scanf (“%d %d”, &m, &n);while(m != 0 && n != 0){if(m > n){m = m % n;}{n = n % m;}}r = m + n;printf(“最大公约数为:%d”, r);return 0;}C语言有着语言特有的表达方式,它和其他语言不同,所以编写C语言程序时,需要有一定的基础。


最大公约数和最小公倍数 c语言最大公约数(GCD)和最小公倍数(LCM)是数学中常见的概念,用于找到一组数的最大公约数和最小公倍数。
最大公约数是指一组数中的最大公约数,即能够同时整除这组数的最大正整数。
用符号GCD(a, b)表示,可以通过欧几里得算法来计算。
最小公倍数是指一组数中的最小公倍数,即可以同时被这组数整除的最小正整数。
用符号LCM(a, b)表示,可以通过以下公式计算:LCM(a, b) = (a * b) / GCD(a, b)C语言代码示例:```c#include <stdio.h>// 计算最大公约数int gcd(int a, int b) {if (b == 0) {return a;} else {return gcd(b, a % b);}}// 计算最小公倍数int lcm(int a, int b) {return (a * b) / gcd(a, b);}int main() {int a, b;printf("请输入两个整数:");scanf("%d %d", &a, &b);printf("最大公约数:%d\n", gcd(a, b));printf("最小公倍数:%d\n", lcm(a, b));return 0;}```这段代码首先定义了两个函数:`gcd`用于计算最大公约数,`lcm`用于计算最小公倍数。
在`main`函数中,通过用户的输入获取两个整数,并调用以上两个函数来计算最大公约数和最小公倍数,最后将结果打印输出。
注:请注意在实际编写代码时,应考虑输入错误或异常情况的处理,例如负数、零等特殊情况。
上述代码只是一个简单示例,可能需要根据实际需求进行修改和完善。

辗转相除法c语言求最大公约数和最小公倍数
1.辗转相除法的用法
最大公约数
辗转相除法是用一个大的数除以一个小的数,如果有余数,就用被除
数➗余数,如果还有余数就继续用(上一个公式的)被除数➗余数,直到
余数为0时停止。
当余数为0的时候,除数➗被除数=商……余数(为0)此时的被除数就是最大公约数(最大公因数)。
例如:。
最小公倍数就等于这两个数的乘积数以最大公约数
例如求a,b的最小公倍数
最小公倍数=a*b/(a与b的最大公约数)
2.代码实现
#include <stdio.h>
int main(
{
int a = 0;
int b = 0;
int c = 0;//余数
int t = 0;
printf("请输入两个数:");
scanf("%d %d",&a,&b);
//判断a,b的大小,大的放在前面
if(b>a)
{
int tmp = a;
a = b;
b = tmp;
}
//因为最小公倍数=a*b/最大公约数
//1.a*b
t = a * b;
//2.最大公约数
while(c=a%b)//如果余数不为零进入循环 {
a = b;//把被除数的值赋给除数
b = c;//把余数的值赋给被除数
}
t = t / b;//最小公倍数
printf("最小公倍数为:%d",t); return 0;
}。
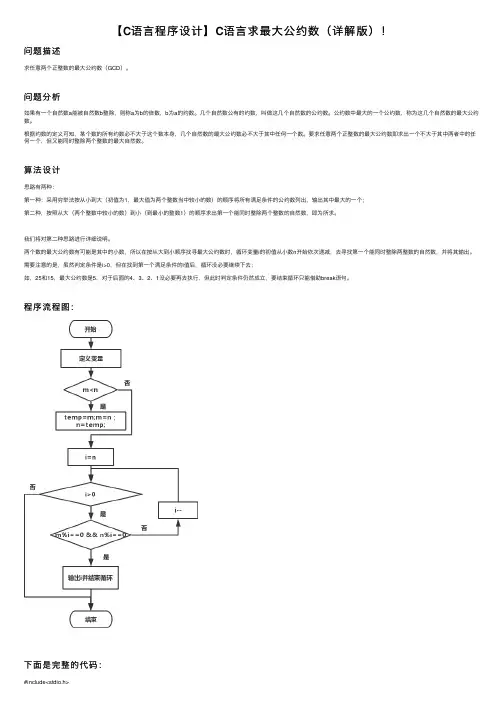
【C语⾔程序设计】C语⾔求最⼤公约数(详解版)!问题描述求任意两个正整数的最⼤公约数(GCD)。
问题分析如果有⼀个⾃然数a能被⾃然数b整除,则称a为b的倍数,b为a的约数。
⼏个⾃然数公有的约数,叫做这⼏个⾃然数的公约数。
公约数中最⼤的⼀个公约数,称为这⼏个⾃然数的最⼤公约数。
根据约数的定义可知,某个数的所有约数必不⼤于这个数本⾝,⼏个⾃然数的最⼤公约数必不⼤于其中任何⼀个数。
要求任意两个正整数的最⼤公约数即求出⼀个不⼤于其中两者中的任何⼀个,但⼜能同时整除两个整数的最⼤⾃然数。
算法设计思路有两种:第⼀种:采⽤穷举法按从⼩到⼤(初值为1,最⼤值为两个整数当中较⼩的数)的顺序将所有满⾜条件的公约数列出,输出其中最⼤的⼀个;第⼆种,按照从⼤(两个整数中较⼩的数)到⼩(到最⼩的整数1)的顺序求出第⼀个能同时整除两个整数的⾃然数,即为所求。
我们将对第⼆种思路进⾏详细说明。
两个数的最⼤公约数有可能是其中的⼩数,所以在按从⼤到⼩顺序找寻最⼤公约数时,循环变量i的初值从⼩数n开始依次递减,去寻找第⼀个能同时整除两整数的⾃然数,并将其输出。
需要注意的是,虽然判定条件是i>0,但在找到第⼀个满⾜条件的i值后,循环没必要继续下去;如,25和15,最⼤公约数是5,对于后⾯的4、3、2、1没必要再去执⾏,但此时判定条件仍然成⽴,要结束循环只能借助break语句。
程序流程图:下⾯是完整的代码:#include<stdio.h>int main(){int m, n, temp, i;printf("Input m & n:");scanf("%d%d", &m, &n);if(m<n) /*⽐较⼤⼩,使得m中存储⼤数,n中存储⼩数*/{ /*交换m和n的值*/temp=m;m=n;n=temp;}for(i=n; i>0; i--) /*按照从⼤到⼩的顺序寻找满⾜条件的⾃然数*/if(m%i==0 && n%i==0){/*输出满⾜条件的⾃然数并结束循环*/printf("The GCD of %d and %d is: %d\n", m, n, i);break;}return0;}运⾏结果:Input m & n:100 125The GCD of 125 and 100 is: 25不管你是转⾏也好,初学也罢,进阶也可,如果你想学编程,进阶程序员~【值得关注】我的!【点击进⼊】全栈程序员正在等你加⼊~。

最大公约数最小公倍数c语言程序最大公约数和最小公倍数是数学中常见的概念,也是计算机编程中常用的算法。
在C语言中,可以通过编写程序来计算最大公约数和最小公倍数。
最大公约数是指两个或多个整数共有约数中最大的一个。
最小公倍数是指两个或多个整数公有倍数中最小的一个。
在C语言中,可以使用辗转相除法来计算最大公约数,使用最大公约数和两个数的乘积来计算最小公倍数。
以下是一个计算最大公约数和最小公倍数的C语言程序:```#include <stdio.h>int gcd(int a, int b) {if (b == 0) {return a;} else {return gcd(b, a % b);}int lcm(int a, int b) {return a * b / gcd(a, b);}int main() {int a, b;printf("Enter two integers: ");scanf("%d %d", &a, &b);printf("GCD of %d and %d is %d\n", a, b, gcd(a, b));printf("LCM of %d and %d is %d\n", a, b, lcm(a, b));return 0;}```在这个程序中,我们定义了两个函数gcd和lcm来计算最大公约数和最小公倍数。
gcd函数使用辗转相除法来计算最大公约数,lcm函数使用最大公约数和两个数的乘积来计算最小公倍数。
在main函数中,我们通过输入两个整数来调用这两个函数,并输出计算结果。
这个程序可以在任何支持C语言的编译器中编译和运行。
它可以计算任意两个整数的最大公约数和最小公倍数,是一个非常实用的工具。
总之,计算最大公约数和最小公倍数是C语言编程中常见的任务。
通过编写程序来计算这些值,我们可以更方便地进行数学计算和问题解决。

c语言编程计算最大公约数,最下公倍数辗转相除法辗转相除法,又称欧几里德算法,是一种用于计算两个整数的最大公约数的算法。
它是由古希腊数学家欧几里德在其著作《几何原本》中首次描述的。
辗转相除法的原理很简单,它基于一个数学定理:两个整数的最大公约数等于其中较小的数和两数相除的余数的最大公约数。
即如果a 和b是两个整数,且a > b,则a和b的最大公约数等于b和a%b的最大公约数。
下面我们用C语言来实现辗转相除法:```c#include <stdio.h>int gcd(int a, int b) {while (b != 0) {int temp = a % b;a = b;b = temp;}return a;}int lcm(int a, int b) { return a * b / gcd(a, b); }int main() {int a, b;printf("请输入两个整数:"); scanf("%d %d", &a, &b);int gcdResult = gcd(a, b);int lcmResult = lcm(a, b);printf("最大公约数是:%d\n", gcdResult);printf("最小公倍数是:%d\n", lcmResult);return 0;}```在上面的代码中,首先定义了两个函数`gcd`和`lcm`分别用于计算最大公约数和最小公倍数。
在`gcd`函数中,我们使用`while`循环来不断更新`a`和`b`的值,直到`b`变为零。
在每次循环中,我们通过`temp`变量暂存`a`对`b`取模的值,并通过赋值语句更新`a`和`b`的值。
当`b`变为零时,循环结束,此时`a`的值就是最大公约数。
在`lcm`函数中,我们通过`a`和`b`的乘积除以最大公约数来计算最小公倍数。
C语⾔实现求最⼤公约数的三种⽅法⽬录题⽬描述问题分析代码实现⽅法⼀:穷举法⽅法⼆:辗转相除法⽅法三:更相减损法题⽬描述求任意两个正整数的最⼤公约数问题分析最⼤公因数,也称最⼤公约数、最⼤公因⼦,指两个或多个整数共有约数中最⼤的⼀个。
a,b的最⼤公约数记为(a,b),同样的,a,b,c的最⼤公约数记为(a,b,c),多个整数的最⼤公约数也有同样的记号。
求最⼤公约数有多种⽅法,常见的有质因数分解法、短除法、辗转相除法、更相减损法。
与最⼤公约数相对应的概念是最⼩公倍数,a,b的最⼩公倍数记为[a,b]。
——百度百科最⼤公因数的求法有不少,本⽂我将采⽤穷举法、辗转相除法、更相减损法三种⽅法,求两个正整数的最⼤公约数(最⼤公因数)。
代码实现⽅法⼀:穷举法穷举法(列举法),是最简单最直观的⼀种⽅法。
具体步骤为:先求出两个数的最⼩值min(最⼤公约数⼀定⼩于等于两个数的最⼩值),接着从最⼩值min递减遍历(循环结束条件为i > 0),如果遇到⼀个数同时为这两个整数的因数,则使⽤break退出遍历(退出循环),这时的遍历值i即为两个正整数的最⼤公约数。
123 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23#include <stdio.h>/*** @brief 获取两个正整数的最⼤公因数(穷举法) * @param num1 第⼀个正整数* @param num2 第⼆个正整数* @return 最⼤公因数*/int Get_Max_Comm_Divisor(int num1, int num2) {int i = 0;//获取两个整数的最⼩值int min = num1 < num2 ? num1 : num2;//从两个数的最⼩值开始递减遍历for(i = min; i > 0; i--){//i为num1和num2的公倍数if(num1 % i == 0 && num2 % i == 0)break;}return i;}2425262728293031int main(){int num1 = 0, num2 = 0;puts("请输⼊两个正整数.");scanf("%d%d", &num1, &num2); printf("最⼤公约数为%d.\n", Get_Max_Comm_Divisor(num1, num2)); return 0;}运⾏结果⽅法⼆:辗转相除法辗转相除法⼜称欧⼏⾥得算法,是指⽤于计算两个⾮负整数a ,b 的最⼤公约数。
C语言最大公约数与最小公倍数在C语言中,可以使用欧几里得算法(辗转相除法)来计算两个数的最大公约数(GCD),然后使用最大公约数和两数乘积的关系计算最小公倍数(LCM)。
#include <stdio.h>// 定义辗转相除法函数,计算最大公约数int gcd(int a, int b) {if (b == 0) {return a;} else {return gcd(b, a % b);}}// 计算最小公倍数,使用最大公约数和两数乘积的关系int lcm(int a, int b) {return (a * b) / gcd(a, b);}int main() {int num1, num2;printf("请输入两个整数:");scanf("%d %d", &num1, &num2);printf("最大公约数为:%d\n", gcd(num1, num2));printf("最小公倍数为:%d\n", lcm(num1, num2));return 0;}在上述示例中,我们首先定义了辗转相除法的函数gcd,用于计算最大公约数。
然后,我们使用最大公约数和两数乘积的关系,定义了计算最小公倍数的函数lcm最后,我们在main函数中从用户输入读取两个整数,并调用gcd和lcm函数计算最大公约数和最小公倍数,并将结果打印输出。
示例程序的输出如下:请输入两个整数:18 24最大公约数为:6最小公倍数为:72在这个例子中,我们输入了两个整数18和24。
程序计算出它们的最大公约数为6,最小公倍数为72。
迭代法求最大公约数和最小公倍数引言最大公约数和最小公倍数是数论中的重要概念,它们在实际应用中经常被用到。
本文将介绍一种用迭代法求解最大公约数和最小公倍数的方法。
最大公约数两个或多个整数的最大公约数(Greatest Common Divisor,简称GCD)是能够同时整除它们的最大整数。
算法思想两个整数的最大公约数可以通过辗转相除法(欧几里德算法)来求解。
迭代的过程是将两个数中较大的数除以较小的数,然后再将所得的余数与较小的数相除,直到余数为0为止,最后的除数就是最大公约数。
代码实现#include <stdio.h>int gcd(int a, int b) {int r;while (b != 0) {r = a % b;a = b;b = r;}return a;}int main() {int a, b;printf("请输入两个整数:");scanf("%d %d", &a, &b);int result = gcd(a, b);printf("最大公约数为:%d\n", result);return0;}最小公倍数两个或多个整数的最小公倍数(Least Common Multiple,简称LCM)是能够同时被它们整除的最小整数。
算法思想两个整数的最小公倍数可以通过求解它们的最大公约数来得到。
根据数学原理,两个整数的乘积等于它们的最大公约数与最小公倍数的积。
因此,我们可以通过最大公约数求得最小公倍数的公式:lcm(a, b) = |a * b| / gcd(a, b)代码实现#include <stdio.h>int gcd(int a, int b) {int r;while (b != 0) {r = a % b;a = b;b = r;}return a;}int lcm(int a, int b) {int result = (a * b) / gcd(a, b);return result;}int main() {int a, b;printf("请输入两个整数:");scanf("%d %d", &a, &b);int result = lcm(a, b);printf("最小公倍数为:%d\n", result);return0;}总结本文介绍了使用迭代法来求解最大公约数和最小公倍数的方法。
c语言计算两个数的最大公约数C语言计算两个数的最大公约数是一个很基础的问题,但对于初学者来说可能会有一定难度。
下面我们来介绍一下如何用C语言计算两个数的最大公约数。
首先,我们需要了解什么是最大公约数。
最大公约数是指两个或多个整数共有约数中最大的一个。
例如,12和18的最大公约数是6。
接下来,我们可以使用辗转相除法来计算两个数的最大公约数。
辗转相除法的基本思想是用较大的数除以较小的数,再用余数去除较小的数,如此反复,直到余数为0为止。
最后被除数就是两个数的最大公约数。
下面是用C语言实现辗转相除法计算最大公约数的代码:```#include <stdio.h>int main(){int num1, num2, remainder, gcd;printf("请输入两个整数:\n");scanf("%d %d", &num1, &num2);while (num2 != 0){remainder = num1 % num2;num1 = num2;num2 = remainder;}gcd = num1;printf("最大公约数为:%d\n", gcd);return 0;}```在这个代码中,我们首先定义了四个变量:num1、num2、remainder和gcd。
num1和num2分别用来存储用户输入的两个整数,remainder用来存储余数,gcd用来存储最大公约数。
接下来,我们使用scanf函数从用户输入中读取两个整数,并将它们存储在num1和num2中。
然后,我们使用while循环来实现辗转相除法。
在每次循环中,我们将num2赋值给remainder,将num1%num2的结果赋值给num1,将remainder的值赋值给num2。
这样反复执行,直到num2的值为0为止。
最后,我们将num1的值赋给gcd,并使用printf函数输出最大公约数的值。
最大公约数c语言编程
// 一般非递归解法
// 首先要求两个整数的最大公约数,需要找到这两个数的公共因子最大的因子,比如10 和 15的最大公约数为5,这里是 10 和 15的公共因子中最大的,因此5为它们的最公约数。
// 下面给出一个 c 语言实现的非递归版本的最大公约数函数:/*
int gcd(int x, int y)
{
int temp;
while(x%y) {
temp=x;
x=y;
y=temp%x;
}
return y;
}
*/
// 上面函数含义是对两个整数 x 和 y 求最大公约数,比如调用
gcd(12, 8),它们最大公约数就是4。
算法运行流程是:如果x除以y 余数不为0,就令temp等于x,x等于y,y等于temp除以x的余数,再进行下一轮循环。
重复刚才的过程,直到 x 除以 y 余数为0,这时的y值就是两个数的最大公约数。