组合逻辑电路设计之全加器、半加器

一、实验目的
1. 掌握组合逻辑电路的功能测试。

2. 验证半加器和全加器的逻辑功能。

3. 学会二进制数的运算规律。

二、实验原理及其实验元件
实验原理：参照指导书对应内容结合自己理解写
实验箱、芯片（74LS00、74LS10、74LS54、74LS86）、导线。

三、实验内容及其步骤
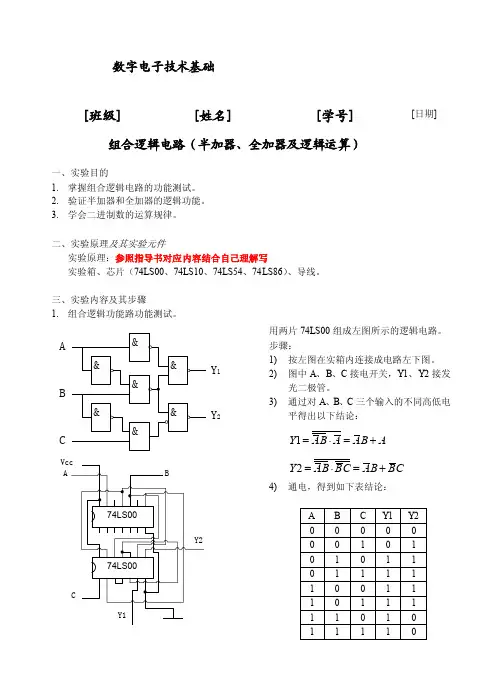
数字电子技术基础
组合逻辑电路（半加器、全加器及逻辑运算）
[班级] [姓名] [学号]
[日期]
2.测试用异或门（74LS86）和与非门组成的半加器的逻辑功能。

用一片（74LS86）和（74LS00）组成半加器。

3.测试用异或门、与或门和非门组成的全加
器的逻辑功能。

S
CO
设计性实验
设计一个“三个一至电路”。

电路有三个输入端，一个输出端。

当三个输入端变量A、B、C状态一致时，输出F为“1”；当三个变量状态不一致时，输出F为“0”。

（要求：用与非门组成电路。

）
步骤：
1)列真值表：
2)写出逻辑表达式:
()()
ABC
C
B
A
F⋅
=
3)画逻辑电路图：
A
B
C
F
4)验证：
所得实验结论与理论值相等，说明实验成功。

5)按下图连接实验电路。

A
B。

全加器与半加器原理及电路设计全加器是一种电子逻辑电路，用于执行二进制加法。

它由三个输入端(A, B, Cin)和两个输出端(S, Cout)组成。

其中，输入端A和B是要相加的二进制位，Cin是前一位的进位，输出端S是和的结果，Cout是是否有进位。

全加器可以通过组合多个半加器来构建。

半加器是全加器的组成部分，它只有两个输入端(A, B)和两个输出端(S, Cout)。

半加器只能够完成一位二进制加法，不考虑进位情况。

其中，输入端A和B是要相加的二进制位，输出端S是和的结果，Cout是是否有进位。

半加器的电路设计相对简单，可以通过逻辑门实现。

接下来，我将详细介绍全加器和半加器的原理和电路设计。

1.半加器原理及电路设计：半加器的真值表如下：A ，B ， S ， Cout0，0，0，00，1，1，01，0，1，01，1，0，1可以看出，输出端S等于两个输入端A和B的异或结果，输出端Cout等于两个输入端A和B的与运算结果。

半加器的电路设计可以使用两个逻辑门实现。

一个逻辑门用于计算和的结果S，另一个逻辑门用于计算进位Cout。

S = A xor BCout = A and B逻辑门可以采用与门、或门和异或门实现。

常用的逻辑门包括与非门(NAND)和异或门(XOR)。

所以，半加器的电路设计可以使用两个与非门和一个异或门实现。

2.全加器原理及电路设计：全加器的真值表如下：A ，B ， Cin ， S ， Cout0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1可以看出，输出端S等于三个输入端A、B和Cin的异或结果，输出端Cout等于输入端A、B和Cin的与运算结果和A和B的或运算结果的与运算结果。

全加器可以由两个半加器和一个或门组成。

其中，两个半加器用于计算S的低位和Cout的低位，而或门用于计算Cout的高位。

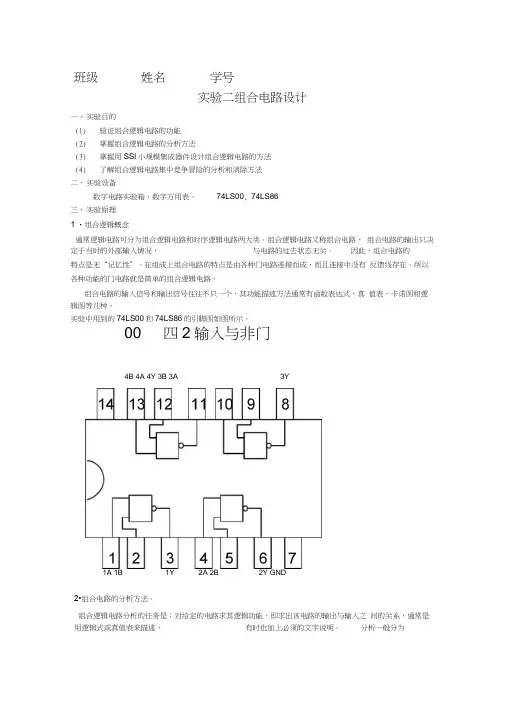
班级姓名学号实验二组合电路设计一、实验目的(1)验证组合逻辑电路的功能(2)掌握组合逻辑电路的分析方法(3)掌握用SSI小规模集成器件设计组合逻辑电路的方法(4)了解组合逻辑电路集中竞争冒险的分析和消除方法二、实验设备数字电路实验箱，数字万用表，74LS00, 74LS86三、实验原理1 •组合逻辑概念通常逻辑电路可分为组合逻辑电路和时序逻辑电路两大类。

组合逻辑电路又称组合电路，组合电路的输出只决定于当时的外部输入情况，与电路的过去状态无关。

因此，组合电路的特点是无“记忆性”。

在组成上组合电路的特点是由各种门电路连接而成，而且连接中没有反馈线存在。

所以各种功能的门电路就是简单的组合逻辑电路。

组合电路的输入信号和输出信号往往不只一个，其功能描述方法通常有函数表达式、真值表，卡诺图和逻辑图等几种。

实验中用到的74LS00和74LS86的引脚图如图所示。

00 四2输入与非门4B 4A 4Y 3B 3A 3Y1A 1B 1Y 2A 2B 2Y GND2•组合电路的分析方法。

组合逻辑电路分析的任务是：对给定的电路求其逻辑功能，即求出该电路的输出与输入之间的关系，通常是用逻辑式或真值表来描述，有时也加上必须的文字说明。

分析一般分为(1)由逻辑图写出输出端的逻辑表达式，简历输入和输出之间的关系。

(2)列出真值表。

(3)根据对真值表的分析，确定电路功能。

3•组合逻辑电路的设计方法。

组合逻辑电路设计的任务是：由给定的功能要求，设计出相应的逻辑电路。

一般设计的逻辑电路的过程如图(1)通过对给定问题的分心，获得真值表。

在分析中要特别注意实际问题如何抽象为几个输入变量和几个输出变量直接的逻辑关系问题，其输出变量之间是否存在约束关系，从而过得真值表或简化真值表。

(2)通过卡诺图化简或逻辑代数化简得出最简与或表达式，必要时进行逻辑式的变更，最后画出逻辑图。

(3)根据最简逻辑表达式得到逻辑电路图。

四•实验内容。

1•分析，测试半加器的逻辑功能。

组合逻辑电路是数字电路中的一种重要类型，主要用于实现逻辑运算和计算功能。

其中，半加器和全加器是组合逻辑电路的两种基本结构，通过它们可以实现数字加法运算。

本文将详细介绍组合逻辑电路的相关知识，包括半加器、全加器以及逻辑运算的原理和应用。

一、半加器半加器是一种简单的数字电路，用于对两个输入进行加法运算，并输出其和及进位。

其结构由两个输入端(A、B)、两个输出端(S、C)组成，其中S表示和，C表示进位。

半加器的真值表如下：A B S C0 0 0 00 1 1 01 0 1 01 1 0 1从真值表可以看出，半加器只能实现单位加法运算，并不能处理进位的问题。

当需要进行多位数的加法运算时，就需要使用全加器来实现。

二、全加器全加器是用于多位数加法运算的重要逻辑电路，它能够处理两个输入以及上一位的进位，并输出本位的和以及进位。

全加器由三个输入端(A、B、Cin)和两个输出端(S、Cout)组成，其中Cin表示上一位的进位，S表示和，Cout表示进位。

全加器的真值表如下：A B Cin S Cout0 0 0 0 00 0 1 1 00 1 0 1 00 1 1 0 11 0 0 1 01 0 1 0 11 1 0 0 11 1 1 1 1通过全加器的应用，可以实现多位数的加法运算，并能够处理进位的问题，是数字电路中的重要组成部分。

三、逻辑运算除了实现加法运算外，组合逻辑电路还可用于实现逻辑运算，包括与、或、非、异或等运算。

这些逻辑运算能够帮助数字电路实现复杂的逻辑功能，例如比较、判断、选择等。

逻辑运算的应用十分广泛，不仅在计算机系统中大量使用，而且在通信、控制、测量等领域也有着重要的作用。

四、组合逻辑电路的应用组合逻辑电路在数字电路中有着广泛的应用，其不仅可以实现加法运算和逻辑运算，还可以用于构建各种数字系统，包括计数器、时序逻辑电路、状态机、多媒体处理器等。

组合逻辑电路还在通信、控制、仪器仪表等领域得到了广泛的应用，为现代科技的发展提供了重要支持。

《数字电路与逻辑设计实验》实验报告实验名称：组合逻辑电路(半加器全加器及逻辑运算)实验器材（芯片类型及数量）7400 二输入端四与非门，7486 二输入端四异或门，7454 四组输入与或非门一、实验原理1、组合逻辑电路的分析方法：（1）从输入到输出，逐步获取逻辑表达式（2）简化逻辑表达式（3）填写真值表（4）通过真值表总结出该电路的功能（5）选择芯片型号，绘制电路图，测试并验证之前的分析是否正确2、组合逻辑电路的设计方法：（1）根据实际逻辑问题的因果关系，定义输入输出变量的逻辑状态（2）根据设计要求，按逻辑功能列出真值表，填写卡诺图（3）通过卡诺图或真值表得到逻辑表达式（4）根据逻辑方程式画出图表，进行功能试验二、实验内容及原理图1、完成与非门、异或门、与或非门逻辑功能测试。

2、测试由异或门和与非门组成的半加器的逻辑功能。

根据半加器的逻辑表达式可知，半加器和位Y是A、B的异或而进位Z是A、B相与，故半加器可用一个继承异或门和两个与非门构成如图2.1。

AYBZ图2.1 半加器电路结构图（1）按照图2.1完成电路连接。

（2）按照表2.1改变A 、B 状态，并填表。

3、 测试全加器的逻辑功能。

SiG9CiA iB iC i-1图2.2 全加器电路结构图（1）写出图2.2的逻辑功能表达式（Y S i C i ） Y = Ai ⊕ Bi Si = Ai ⊕ Bi ⊕ Ci -1 Ci = AiBi + (Ai ⊕ Bi) Ci -1 （2）根据逻辑功能表达式列出真值表（3）按原理图选择与非门并接线测试，将结果记入表2.2。

4、 用异或、与或非门和与非门实现全加器的逻辑功能。

全加器可以用两个半加器和两个与门一个或门组成，在实验中，常用一块双异或门、一个与或非门和一个与非门实现。

（1）画出用异或门、与或非门和非门实现全加器的逻辑电路图，写出逻辑表达式。

Y = Ai ⊕ Bi Si = Ai ⊕ Bi ⊕ Ci -1 Ci = AiBi + (Ai ⊕ Bi) Ci -1（2）找出异或门、与或非门和与非门器件按自己画的图接线。

组合逻辑电路实验（半加器全加器及逻辑运算）一、实验目的1、掌握组合逻辑电路的功能测试。

2、验证半加器和全加器的逻辑功能。

3、学会二进制数的运算规律。

二、实验原理数字电路分为组合逻辑电路和时序逻辑电路两类。

任意时刻电路的输出信号仅取决于该时刻的输入信号，而与信号输入前电路所处的状态无关，这种电路叫做组合逻辑电路。

分析一个组合电路，一般从输出开始，逐级写出逻辑表达式，然后利用公式或卡诺图等方法进行化简，得到仅含有输入信号的最简输出逻辑函数表达式，由此得到该电路的逻辑功能。

两个一位二进制数相加，叫做半加，实现半加操作的电路称为半加器。

两个一位二进制数相加的真值表见表5-1，表中Si表示半加和，Ci表示向高位的进位，Ai、Bi表示两个加数。

表5-1 半加器真值表从二进制数加法的角度看，表中只考虑了两个加数本身，没有考虑低位来的进位，这也就是半加一词的由来。

由表5-1可直接写出半加器的逻辑表达式： 、Ci=AiBi由逻辑表达式可知，半加器的半加和Si是Ai、Bi的异或，而进Si=AiBi AiBi位Ci 是Ai 、Bi 相与，故半加器可用一个集成异或门和一个与门组成。

两个同位的加数和来自低位的进位三者相加，这种加法运算就是全加，实现全加运算的电路叫做全加器。

如果用Ai 、Bi 分别表示A 、B 两个多位二进制数的第i 位，1i C -表示低位（第i-1位）来的进位，则根据全加运算的规则可列出真值表如表5-2。

表5-2 全加器的真值表利用卡诺图可求出Si 、Ci 的简化函数表达式：i i i i-1i i i i i i S =A B C C =(A B )C +A B ⊕⊕⊕可见，全加器可用两个异或门和一个与或门组成。

如果将数据表达式进行一些变换，半加器还可以用异或门、与非门等元器件组成多种形式的电路（见图5-2，图5-3）。

三、实验仪器及材料 器件：74LS00 二输入端四与非门 3片 74LA86 二输入端四异或门 1片 74LS54 四组输入与或非门 1片四、预习要求1、预习组合逻辑电路的分析方法。

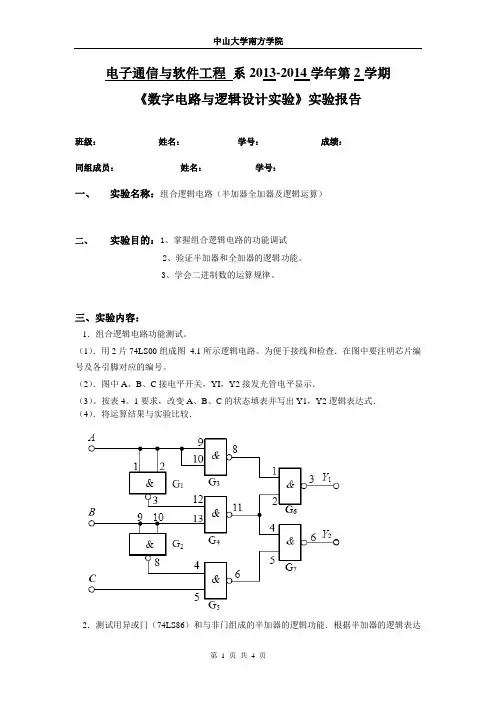
电子通信与软件工程系2013-2014学年第2学期《数字电路与逻辑设计实验》实验报告--------------------------------------------------------------------------------------------------------------------- 班级：姓名：学号：成绩：同组成员：姓名：学号：---------------------------------------------------------------------------------------------------------------------一、实验名称：组合逻辑电路（半加器全加器及逻辑运算）二、实验目的：1、掌握组合逻辑电路的功能调试2、验证半加器和全加器的逻辑功能。

3、学会二进制数的运算规律。

三、实验内容：1．组合逻辑电路功能测试。

（1）．用2片74LS00组成图4.1所示逻辑电路。

为便于接线和检查．在图中要注明芯片编号及各引脚对应的编号。

（2）．图中A、B、C接电平开关，YI，Y2接发光管电平显示．（3）。

按表4。

1要求，改变A、B、C的状态填表并写出Y1，Y2逻辑表达式．（4）．将运算结果与实验比较．2．测试用异或门（74LS86）和与非门组成的半加器的逻辑功能．根据半加器的逻辑表达式可知．半加器Y是A、B的异或，而进位Z是A、B相与，故半加器可用一个集成异或门和二个与非门组成如图4.2．（1）．在学习机上用异或门和与门接成以上电路．接电平开关S．Y、Z接电平显示．（2）．按表4．2要求改变A、B状态，填表．3．测试全加器的逻辑功能。

（1）．写出图4．3电路的逻辑表达式。

（2）．根据逻辑表达式列真值表．（3）．根据真值表画逻辑函数S i 、Ci的卡诺图．（4）．填写表4．3各点状态（5）．按原理图选择与非门并接线进行测试，将测试结果记入表4．4，并与上表进行比较看逻辑功能是否一致．实验结果：表4．1Y1=A+B Y2=（A’·B）+（B’·C）表4．2表4．3表4．4Y=A’B+AB’Z=CX1=A’B+C’+AB X2=A’B’+AB+C X3=A’B+AB’+C’Si=A’B’C+A’BC’+AB’C+ABC Ci=AC+AB+BC实验总结：此实验中因本就缺少一块74LS00的芯片导致线路不完整，原本打算用74LS20来代替74LS00，但电路还是出现了问题，原以为是电路接线的问题，也重新接线过，但是情况毫无变化。

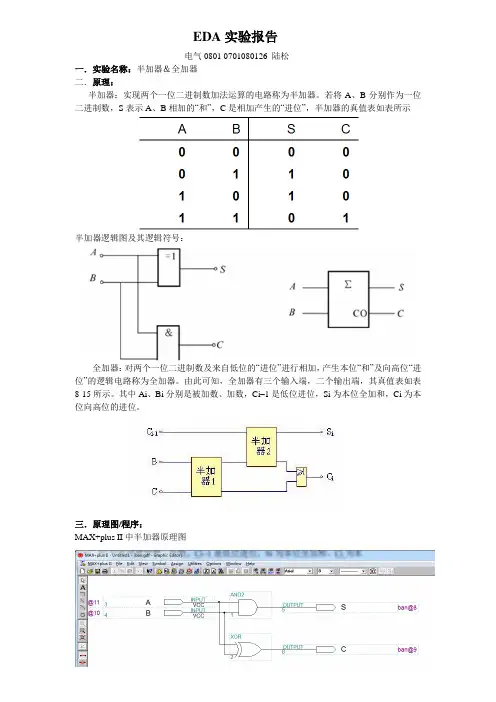
EDA实验报告电气0801 0701080126 陆松一．实验名称：半加器＆全加器二．原理：半加器：实现两个一位二进制数加法运算的电路称为半加器。

若将A、B分别作为一位二进制数，S表示A、B相加的“和”，C是相加产生的“进位”，半加器的真值表如表所示半加器逻辑图及其逻辑符号：全加器：对两个一位二进制数及来自低位的“进位”进行相加，产生本位“和”及向高位“进位”的逻辑电路称为全加器。

由此可知，全加器有三个输入端，二个输出端，其真值表如表8-15所示。

其中Ai、Bi分别是被加数、加数，Ci–1是低位进位，Si为本位全加和，Ci为本位向高位的进位。

三．原理图/程序：MAX+plus II中半加器原理图VHDL程序：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY HALF_ADDER ISPORT(A,B:IN STD_LOGIC;S,CO:OUT STD_LOGIC);END HALF_ADDER;ARCHITECTURE HALF_ADDER OF HALF_ADDER IS COMPONENT HALF_ADDERPORT(A,B:IN STD_LOGIC;S,CO:OUT STD_LOGIC);END COMPONENT;BEGINS<='0' WHEN A='0' AND B='0' ELSE'1'WHEN A='0' AND B='1' ELSE'1' WHEN A='1' AND B='0' ELSE'0' WHEN A='1' AND B='1';CO<='0' WHEN A='0' AND B='0' ELSE'0' WHEN A='0' AND B='1' ELSE'0' WHEN A='1' AND B='0' ELSE'1' WHEN A='1' AND B='1';END HALF_ADDER;MAX+plus II中全加器原理图VHDL程序：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY FULL_SUBER ISPORT(A,B,CIN:IN STD_LOGIC;CO,S:OUT STD_LOGIC);END FULL_SUBER;ARCHITECTURE FULL OF FULL_SUBER IS COMPONENT HALF_SUBERPORT(A,B:IN STD_LOGIC;S,CO:OUT STD_LOGIC);END COMPONENT;SIGNAL S1,S2,S3:STD_LOGIC;BEGINU0:HALF_SUBER PORT MAP(A,B,S2,S1);U1:HALF_SUBER PORT MAP(S2,CIN,S,S3);CO<=S1 OR S3;END FULL;四．实验步骤：步骤1：为本项工程设计建立文件夹，文件夹不能为中文名。

班级姓名学号实验二组合电路设计一、实验目的（1）验证组合逻辑电路的功能掌握组合逻辑电路的分析方法掌握用SSI小规模集成器件设计组合逻辑电路的方法了解组合逻辑电路集中竞争冒险的分析和消除方法实验设备数字电路实验箱，数字万用表，74LS00，74LS86三、实验原理1．组合逻辑概念通常逻辑电路可分为组合逻辑电路和时序逻辑电路两大类。

组合逻辑电路又称组合电路，组合电路的输出只决定于当时的外部输入情况，与电路的过去状态无关。

因此，组合电路的特点是无“记忆性”。

在组成上组合电路的特点是由各种门电路连接而成，而且连接中没有反馈线存在。

所以各种功能的门电路就是简单的组合逻辑电路。

组合电路的输入信号和输出信号往往不只一个，其功能描述方法通常有函数表达式、真值表，卡诺图和逻辑图等几种。

实验中用到的74LS00和74LS86的引脚图如图所示。

00 四2输入与非门Vcc4B4A4Y3B3A3Y Array 1A1B1Y2A2B2Y GND2.组合电路的分析方法。

组合逻辑电路分析的任务是：对给定的电路求其逻辑功能，即求出该电路的输出与输入之间的关系，通常是用逻辑式或真值表来描述，有时也加上必须的文字说明。

分析一般分为一下几个步骤：由逻辑图写出输出端的逻辑表达式，简历输入和输出之间的关系。

列出真值表。

根据对真值表的分析，确定电路功能。

3.组合逻辑电路的设计方法。

组合逻辑电路设计的任务是：由给定的功能要求，设计出相应的逻辑电路。

一般设计的逻辑电路的过程如图：通过对给定问题的分心，获得真值表。

在分析中要特别注意实际问题如何抽象为几个输入变量和几个输出变量直接的逻辑关系问题，其输出变量之间是否存在约束关系，从而过得真值表或简化真值表。

通过卡诺图化简或逻辑代数化简得出最简与或表达式，必要时进行逻辑式的变更，最后画出逻辑图。

根据最简逻辑表达式得到逻辑电路图。

四．实验内容。

1.分析，测试半加器的逻辑功能。

（1）用74LS00组成半加器电路如图所示。

组合逻辑电路设计之全加器半加器全加器和半加器是组合逻辑电路中常用的两种基本电路。

全加器和半加器可以用于实现二进制数的加法运算。

在本文中，将详细介绍全加器和半加器的设计原理和电路结构。

一、半加器半加器是一个用于实现两个一位二进制数相加求和的电路。

半加器的输入包括两个二进制数A和B，输出包括二进制求和信号S和进位信号C。

```A----，--?--SB----，，--CGND```半加器的输出S等于输入A和B的异或（XOR）结果，输出C等于输入A和B的与（AND）结果。

半加器的真值表如下所示：A，B，S，C---，---，---，---0，0，0，00，1，1，01，0，1，01，1，0，1二、全加器全加器是一个用于实现三个一位二进制数相加求和的电路。

全加器的输入包括两个二进制数A和B，以及一个进位信号Cin（来自上一位的进位或者是初始进位信号），输出包括二进制求和信号S和进位信号Cout （输出给下一位的进位信号）。

```A----，--?---SB ----，，--CoutCin --，--?-------CGND```全加器的输出S等于输入A、B和Cin的异或（XOR）结果，输出Cout等于输入A、B和Cin的任意两个的与（AND）结果和输入A、B和Cin的三个的或（OR）结果的与（AND）结果。

全加器的真值表如下所示：A ，B ， Cin ， S ， Cout---，---，-----，---，------0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1三、全加器的电路设计可以通过组合半加器的方式来设计一个全加器。

在全加器中，首先使用两个半加器实现输入A和B的求和结果（S1）和对应的进位（C1）；然后再使用一个半加器将输入A和B之间的进位信号（Cin）与求和结果（S1）相加，得到最终的求和结果（S）和进位信号（Cout）。

实验二组合逻辑电路设计（半加器、全加器）一、半加器.说明：其中A为加数，B为被加数，Y为A、B的和与它们同位的部分，Z为它们的和中向高位的进位部分。

真值表如图示：Array其逻辑函数式为：Y=A’B+AB’Z=AB如果用74ls138做半加器。

图为74LS138的真值表：由真值表得：由Y=A’B+AB’=m1+m2=(m1’.m2’)’Z=AB=(m3’)’二、 全加器说明：其中A 为加数，B 为被加数，C 为低位向高位的进位， Y 为A 、B 得和与他们同位部分，Z 为它们的和中向高位的进位部分。

真值表如图示： 由表得：Y=A ’BC ’+AB ’C ’+A ’B ’C+ABC =m 2+m 4+m 1+m 7= (m 2’·m 4’·m 1’·m 7’)’Z=ABC ’+A ’BC+AB ’C+ABC =m 6+m 3+m 5+m 7=(m 6’·m 3’·m 5’·m 7’)’1、若用与非门、反相器、异或门做，由卡洛图得Z 。

Z 有： Z=AB+BC+AC=((((AB)’(BC)’)’)’(AC)’)’Z 逻辑函数图为：若不用卡洛图化简： 则：Z= ABC ’+A ’BC+AB ’C+ABC=AB(C ’+C)+C(A ⊕B) =((AB)’·(C(A ⊕B))’)’ 逻辑函数图为：2、由于Y用卡洛图无法化简，即已为最简，但没有三输入与非门只有二输入的。

故Y化简为：Y=A’BC’+AB’C’+A’B’C+ABC=C’(A⊕B)+C(A⊙B)=(( C’(A⊕B))’·(C(A⊙B)’)’Y的逻辑图为：用与非门做若用74LS138做：Y的逻辑函数式及测试真值表为如图：Z的逻辑函数表达式及测试真值表如图示：。

组合逻辑电路的设计及半加器全加器组合逻辑电路的设计首先需要确定所需的逻辑功能。

常见的逻辑门包括与门、或门、非门、异或门等。

这些逻辑门可以通过晶体管、二极管等电子元件实现。

设计组合逻辑电路的目标是确定所需的逻辑门类型和电路连接方式，以实现预期的逻辑功能。

半加器是一种实现二进制加法运算的电路。

它有两个输入（被加数和加数）和两个输出（和与进位）。

半加器可以用两个异或门和一个与门实现。

两个输入通过两个异或门进行异或运算，得到和，再通过一个与门计算进位。

全加器是一种实现三个二进制数相加的电路，包括两个被加数和一个进位。

全加器有三个输入（两个被加数和进位）和两个输出（和与进位）。

全加器可以用两个半加器和一个或门实现。

首先，通过一个半加器计算两个被加数的和与进位，再通过另一个半加器计算前一步的和与进位与进位的和与进位。

在实际应用中，半加器和全加器经常被用于数字逻辑电路和计算机中。

它们在二进制加法运算中起着重要的作用。

例如，计算机中的加法器、减法器、乘法器和除法器等都需要使用半加器和全加器进行二进制数的运算。

此外，半加器和全加器还可以作为其他逻辑电路的构建模块，实现更复杂的逻辑功能。

总结起来，组合逻辑电路是由多个逻辑门组成的电路，用于实现特定的逻辑功能。

半加器和全加器是组合逻辑电路的重要组成部分，用于实现二进制加法运算。

它们在数字逻辑电路和计算机中起着重要的作用，并可以作为其他逻辑电路的构建模块。

组合逻辑电路的设计需要确定所需的逻辑功能，并确定适合的逻辑门类型和电路连接方式。

这些设计原理和应用为数字电路领域的进一步研究和应用提供了基础。

班级 姓名 学号实验二 组合电路设计一、实验目的（1） 验证组合逻辑电路的功能 （2） 掌握组合逻辑电路的分析方法（3） 掌握用SSI 小规模集成器件设计组合逻辑电路的方法 （4） 了解组合逻辑电路集中竞争冒险的分析和消除方法 二、实验设备数字电路实验箱，数字万用表，74LS00，74LS86 三、实验原理 1．组合逻辑概念通常逻辑电路可分为组合逻辑电路和时序逻辑电路两大类。

组合逻辑电路又称组合电路，组合电路的输出只决定于当时的外部输入情况，与电路的过去状态无关。

因此，组合电路的特点是无“记忆性”。

在组成上组合电路的特点是由各种门电路连接而成，而且连接中没有反馈线存在。

所以各种功能的门电路就是简单的组合逻辑电路。

组合电路的输入信号和输出信号往往不只一个，其功能描述方法通常有函数表达式、真值表，卡诺图和逻辑图等几种。

实验中用到的74LS00和74LS86的引脚图如图所示。

2.组合电路的分析方法。

组合逻辑电路分析的任务是：对给定的电路求其逻辑功能，即求出该电路的输出与输入之间的关系，通常是用逻辑式或真值表来描述，有时也加上必须的文字说明。

分析一般分为一Vcc4B 4A4Y3B3A3Y1A1B1Y2A2B2YGND00 四2输入与非门下几个步骤：（1）由逻辑图写出输出端的逻辑表达式，简历输入和输出之间的关系。

（2）列出真值表。

（3）根据对真值表的分析，确定电路功能。

3.组合逻辑电路的设计方法。

组合逻辑电路设计的任务是：由给定的功能要求，设计出相应的逻辑电路。

一般设计的逻辑电路的过程如图：（1）通过对给定问题的分心，获得真值表。

在分析中要特别注意实际问题如何抽象为几个输入变量和几个输出变量直接的逻辑关系问题，其输出变量之间是否存在约束关系，从而过得真值表或简化真值表。

（2）通过卡诺图化简或逻辑代数化简得出最简与或表达式，必要时进行逻辑式的变更，最后画出逻辑图。

（3）根据最简逻辑表达式得到逻辑电路图。

四．实验内容。

实验四组合逻辑电路的设计及半加器、全加器一、实验目的1.掌握组合逻辑电路的设计与测试方法2.掌握半加器、全加器的工作原理。

二、实验原理和电路1、组合逻辑电路的设计使用中、小规模集成电路来设计组合电路是最常见的逻辑电路。

设计组合电路的一般步骤如图图1.4.1 组合逻辑电路设计流程图根据设计任务的要求建立输入、输出变量，并列出真值表。

然后用逻辑代数或卡诺图化简法求出简化的逻辑表达式。

并按实际选用逻辑门的类型修改逻辑表达式。

根据简化后的逻辑表达式，画出逻辑图，用标准器件构成逻辑电路。

最后，用实验来验证设计的正确性。

1.半加器根据组合电路设计方法，首先列出半加器的真值表，见表写出半加器的逻辑表达式S=AB+AB=A⊕BC=AB若用“与非门”来实现，即为半加器的逻辑电路图如图在实验过程中，我们可以选异或门74LS86及与门74LS08实现半加器的逻辑功能；也可用全与非门如74LS00反相器74LS04组成半加器。

(a)用异或门组成的半加器 （b ）用与非门组成的半加器图1.4.2 半加器逻辑电路图2.全加器用上述两个半加器可组成全加器，原理如图图 表1.4.2 全加器逻辑功能表表1.4.1 半加器逻辑功能三、实验内容及步骤1.测试用异或门（74LS86）和与非门组成的半加器的逻辑功能。

根据半加器的逻辑表达式可知，相加的和Y 是A 、B 的异或，而进位Z 是A 、B 相与，故半加器可用一个集成异或门和二个与非门组成如图图1.4.4 用一个集成异或门和二个与非门组成半加器⑴ 在实验仪上用异或门和与门接成以上电路。

A 、B 接逻辑开关，Y 、Z 接发光二极管显示。

⑵ 按表，将相加的和Y 和进位Z 的状态填入下表中。

表1.4.3⑴写出图i C i = ⑵根据逻辑表达式列真值表，并完成表1.4.4，实验证之。

⑶根据真值表画逻辑函数SiCi 的卡诺图。

完成图1.4.6图 1.4.5图 1.4.6⑸试设计用异或门、与门、或门组成的全加器的逻辑功能并接线进行测试，将测试结果记入表，与上表进行比较看逻辑功能是否一致。