传热过程的计算
- 格式:doc
- 大小:2.33 MB
- 文档页数:17





第四节 传热过程计算化工原理中所涉及的传热过程计算主要有两类:一类是设计计算,即根据生产要求的热负荷,确定换热器的传热面积;另一类是校核计算,即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算的基础。
应用前述的热传导速率方程和对流传热速率方程时,需要知道壁面的温度。
而实际上壁温常常是未知的,为了避开壁温,故引出间壁两侧流体间的总传热速率方程。
4—4—1 能量衡算对间壁式换热器做能量衡算,以小时为基准,因系统中无外功加入,且一般位能和动能项均可忽略,故实质上为焓衡算。
假设换热器绝热良好,热损失可以忽略时,则在单位时间内换热器中热流体放出的热量等于冷流体吸收的热量,即 , .、)()(1221c c c h h h H H W H H W Q -=-= (4—30)式中 Q —换热器的热负荷,kj/h 或W ;W -流体的质量流量,kg /h ;H -单位质量流体的焓,kJ /kg 。
下标c 、h 分别表示冷流体和热流体,下标1和2表示换热器的进口和出口。
式4-30即为换热器的热量衡算式,它是传热计算的基本方程式,通常可由该式计算换热器的传热量(又称热负荷)。
.若换热器中两流体无相变化,且流体的比热容不随温度而变或可取平均温度下的比热容时,式4-30可表示为Q )()(1221t t c W T T c W pc c ph h -=-= (4-31)式中 c p -流体的平均比热容,kJ /(kg ·℃);t —冷流体的温度,℃;T -热流体的温度,℃。
若换热器中的热流体有相变化,例如饱和蒸气冷凝时,式4-30可表示为Q )(12t t c W r W pc c h -== (4-32)式中 W h —饱和蒸气(即热流体)的冷凝速率,k 2/h ;r —饱和蒸气的冷凝潜热,kJ /kg 。
式4-32的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时,则式4-32变为Q )()]([1221t t c W T T c r W pc c ph h -=-+= (4-33)式中 C ph -冷凝液的比热容,kJ /(kg ·℃);T s —冷凝液的饱和温度,℃。





6.6 传热过程的计算工业上大量存在传热过程(我们指间壁式传热过程),他包括了流体与固体表面间的给热和固体内部的导热。
前面我们已经学过了导热和各种情况下的给热所遵循的规律,本节讨论传热过程的计算问题。
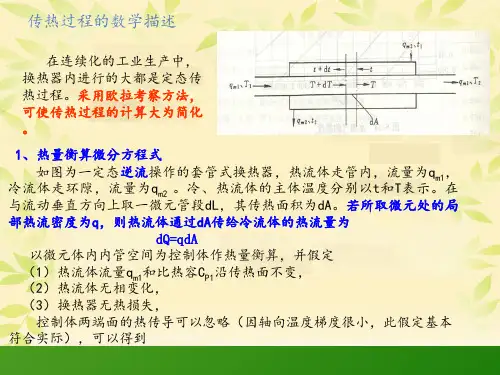
6.6.1 传热过程的数学描述在连续化的工业生产中,换热器内进行的大都是定态传热过程。
(1)热量衡算微分方程式如图为一套管式换热器,内管为传热管,传热管外径1d ,内径2d ,微元传热管外表面积d A 1,管外侧1α;内表面积d A 2,内侧2α,平均面积d A m ,壁面导热系数λ。
对微元体做热量衡算得 Q A q T c m p s d d d 11==-Q A q T c m p s d d d 22==-以上两式是在以下的假设前提下:① 热流体流量1s m 和比热1p c 沿传热面不变;② 热流体无相变化; ③ 换热器无热损失;④ 控制体两端面的热传导可以忽略。
(2)微元传热速率方程式如图所示套管换热器中,热量由热流体传给管壁内侧,再由管壁内侧传至外侧,最后由管壁外侧传给冷流体。
对上述微元,我们可以得到33211321d d d d d d d A q A q A q Q Q Q Q m =======阻力推动力=++-=-=-=-22m 1122w m w w 11w d 1d d 1d 1d d 1A A b A t T A t t A b t T A T T αλααλα 令 2211d 1d d 1d 1A A b A A K m αλα++= 则 )(d d 1d t T A K A K tT Q -=-=)(d d t T K AQ q -==式中 K ——总传热系数,W/m 2·K 。
因为沿着流体流动方向(套管换热器沿管长)流体的温度是变化的,所以α值也是变化的。
但若取一定性温度,则α与传热面无关,可以认为是一常数,这样K 也为一常数。
对上式进行积分,可以得到m t KA Q ∆= (3)传热系数和热阻 ① K 的计算由前面的分析可知,传热过程的总热阻1/K 由各串联环节的热阻叠加而成,原则上减小任何环节的热阻都可提高传热系数,增大传热过程的速率。
第三节 传热基本方程及传热计算从传热基本方程 m t kA Q ∆= (4-11)或传热热阻传热推动力=∆=kA t Q m 1 (4-11a)可知,要强化传热过程主要应着眼于增加推动力和减少热阻,也就是设法增大m t∆或者增大传热面积A和传热系数K。
在生产上,无论是选用或设计一个新的换热器还是对已有的换热器进行查定,都是建立在上述基本方程的基础上的,传热计算则主要解决基本方程中的m t K A Q ∆,,,及有关量的计算。
传热基本方程是传热章中最主要的方程式。
一、传热速率Q的计算冷、热流体进行热交换时,当热损失忽略,则根据能量守恒原理,热流体放出热量h Q ,必等于冷流体所吸收的热量c Q ,即c n Q Q =,称之热量衡算式。
1. 1. 无相变化时热负荷的计算 (1) (1) 比热法()()1221t t c m T T c m Q pc c ph h -=-=(4-12)式中 Q ——热负荷或传热速率,J.s -1或W ; c h m m ,——热、冷流体的质量流量,kg.s -1;ph pc cc ,——冷、热流体的定压比热,取进出口流体温度的算术平均值下的比热, k J.(kg.k )-1;21,T T ——热流体进、出口温度,K(°C ); 21,t t -冷流体的进出口温度,K(°C )。
(2)热焓法)(21I I m Q -= (4-13)式中 1I ——物料始态的焓,k J.kg -1; 2I ——物料终态的焓,k J.kg -1。
2.有相变化时热负荷计算Gr Q = (4-14)式中 G ——发生相变化流体的质量流量,kg.s -1;r ——液体汽化(或蒸汽冷凝)潜热,k J.kg -1。
注意:在热负荷计算时,必须分清有相变化还是无相变化,然后根据不同算式进行计算。
对蒸汽的冷凝、冷却过程的热负荷,要予以分别计算而后相加。
当要考虑热损失时,则有:损Q Q Q c h +=通常在保温良好的换热器中可取h Q Q )(损%5~2=三、平均温度差m t ∆的计算在间壁式换热器中,m t ∆的计算可分为以下几种类型:1. 1.两侧均为恒温下的传热两侧流体分别为蒸汽冷凝和液体沸腾时,温度不变,则:m t ∆=T-t =常数 2. 2.一侧恒温一侧变温下的传热 可推得计算式为:()()21212121ln ln t t t t t T t T t T t T t m ∆∆∆-∆=-----=∆ (4-15)式中m t ∆为进出口处传热温度差的对数平均值,温差大的一端为1t ∆,温差小的一端为2t ∆,从而使上式中分子分母均为正值。
1 总传热速率方程如图所示,以冷热两流体通过圆管的间壁进行换热为例,热流体走管内,温度为T,冷流体走管外温度为t,管壁两侧温度分别为TW和tw,壁厚为,b,其热导率为λ,内外两侧流体与固体壁面间的表面传热系数分别为αi和α0。
根据牛顿冷却定律及傅立叶定律分别列出对流传热及导热的速率方程:对于管内侧:对于管壁导热:对于管外侧:即故有令(4.6.1)则(4.1.1)该式称为总传热速率方程。
A为传热面积,可以是内外或平均面积,K与A是相对应的。
2 热流量衡算热流量衡算式反映两流体在换热过程中温度变化的相互关系,在换热器保温良好,无热损失的情况下,对于稳态传热过程,其热流量衡算关系为:(热流体放出的热流量)=(冷流体吸收的热流量)在进行热衡算时,对有、无相变化的传热过程其表达式又有所区别。
(1)无相变化传热过程式中Q----冷流体吸收或热流体放出的热流量,W;mh,mc-----热、冷流体的质量流量,kg/s;Cph,Cpc------热、冷流体的比定压热容,k J/(kg·K);T1,t1 ------热、冷流体的进口温度,K;T2,t2------热、冷流体的出口温度,K。
(2)有相变化传热过程两物流在换热过程中,其中一侧物流发生相变化,如蒸汽冷凝或液体沸腾,其热流量衡算式为:一侧有相变化两侧物流均发生相变化,如一侧冷凝另一侧沸腾的传热过程式中r,r1,r2--------物流相变热,J/kg;D,D1,D2--------相变物流量,kg/s。
对于过冷或过热物流发生相变时的热流量衡算,则应按以上方法分段进行加和计算。
3 传热系数和传热面积(1)传热系数K和传热面积A的计算传热系数K是表示换热设备性能的极为重要的参数,是进行传热计算的依据。
K的大小取决于流体的物性、传热过程的操作条件及换热器的类型等,K值通常可以由实验测定,或取生产实际的经验数据,也可以通过分析计算求得。
传热系数K可利用式(4.6.1)进行计算。
第五节 传热过程的计算化工生产中广泛采用间壁换热方法进行热量的传递。
间壁换热过程由固体壁的导热和壁两侧流体的对流传热组合而成,导热和对流传热的规律前面已讨论过,本节在此基础上进一步讨论传热的计算问题。
化工原理中所涉及的传热过程计算主要有两类:一类是设计计算,即根据生产要求的热负荷,确定换热器的传热面积;另一类是校核计算,即计算给定换热器的传热量、流体的流量或温度等。
两者都是以换热器的热量衡算和传热速率方程为计算基础。
4-5-1 热量衡算流体在间壁两侧进行稳定传热时,在不考虑热损失的情况下,单位时间热流体放出的热量应等于冷流体吸收的热量,即:Q=Q c =Q h (4-59) 式中 Q ——换热器的热负荷,即单位时间热流体向冷流体传递的热量,W ; Q h ——单位时间热流体放出热量,W ; Q c ——单位时间冷流体吸收热量,W 。
若换热器间壁两侧流体无相变化,且流体的比热容不随温度而变或可取平均温度下的比热容时,式(4-59)可表示为()()1221t t c W T T c W Q pc c ph h -=-= (4-60) 式中 c p ——流体的平均比热容,kJ/(kg ·℃); t ——冷流体的温度,℃; T ——热流体的温度,℃; W ——流体的质量流量,kg/h 。
若换热器中的热流体有相变化,例如饱和蒸气冷凝,则()12t t c W r W Q pc c h -== (4-61) 式中 W h ——饱和蒸气(即热流体)的冷凝速率,kg/h ; r ——饱和蒸气的冷凝潜热,kJ/kg 。
式(4-61)的应用条件是冷凝液在饱和温度下离开换热器。
若冷凝液的温度低于饱和温度时,则式(4-61)变为()[]()122t t c W T T c r W Q pc c s ph h -=-+= (4-62) 式中 c ph ——冷凝液的比热容,kJ/(kg ·℃); T s ——冷凝液的饱和温度,℃。
4-5-2 总传热速率微分方程图4-20为一逆流操作的套管换热器的微元管段d L ,该管段的内、外表面积及平均传热面积分别为d S i 、d S o 和d S m 。
热流依次经过热流体、管壁和冷流体这三个环节,在稳定传热的情况下,通过各环节的传热速率应相等,即oWm W W i W \S t t S b t T S T T Q d 1d d 1d 21αλα-=-=-=(4-63)式中 t W 、T W ——分别为冷热流体侧的壁温,℃; α1、α2——分别为传热管壁内、外侧流体的对 流传热系数,W/(m 2·℃); λ——管壁材料的导热系数,W/(m ·℃); b ——管壁厚度,m ;S i ,S o ,S m ——换热器管内表面积、外表面积和内、外表面平均面积,m 2。
图4-20 微元管段上的传热式(4-63)可改写为总阻力总推动力=++-=om i S S b S t T Q d 1d d 1d 21αλα (4-64)式中i S d 11α、m S d 1λ、oS d 12α——分别为各传热环节的热阻,℃/W 。
由上式我们再次看到,串联过程的推动力与阻力具有加和性。
令 o m i S S b S S K d 1d d 1d 121αλα++= (4-65)则式4-65化为d Q =K d S (T -t ) (4-66) 上式即为总传热速率方程的微分表达式。
式中 d S ——微元管段的传热面积,m 2;K ——定义在d S 上的总传热系数,W/(m 2·℃)。
式4-66表明总传热系数在数值上等于单位温度差下的总传热通量,它表示了冷、热流体进行传热的一种能力,总传热系数的倒数1/K 代表间壁两侧流体传热的总热阻。
4-5-3 总传热系数K一、总传热系数K 的计算表达式总传热系数必须和所选择的传热面积相对应,选择的传热面积不同,总传热系数的数值也不同。
1.传热面为平壁 此时d S o =d S i =d S m ,则由式4-65得到21111αλα++=b K (4-67)2.传热面为圆筒壁 此时,d S o 与d S i 及d S m 三者不相等,由式4-65得21d d d d d d 1S S S S b S S K m i αλα++= (4-68)显然,K 的大小与d S 取值有关,d S 值一般取外表面积d S o 值,则K 值称为以外表面积为基准的总传热系数。
式4-68化为211d d d d 1αλα++=m o i o o S S b S S K / (4-69)或 2111αλα++=m o i o o d bd d d K / (4-70)式中 d i ,d o ,d m ——管内径、管外径和管内、外径的平均直径,m 。
同理可得o i m i i d d d bd K 2111αλα++= (4-70a )o m i m m d d b d d K 211αλα++= (4-70b )式中 K i 、K m ——基于管内表面积和管平均表面积的总传热系数。
3.污垢热阻(又称污垢系数)换热器的实际操作中,传热表面上常有污垢积存,对传热产生附加热阻,使总传热系数降低。
由于污垢层的厚度及其导热系数难以测量,因此通常选用污垢热阻的经验值作为计算K 值的依据。
若管壁内、外侧表面上的污垢热阻分别用R si 及R so 表示,则式4-70变为 2111αλα++++=so m o i o si i o o R d bd d d R d d K (4-71)式中 R si ,R so ——分别为管内和管外的污垢热阻,又称污垢系数,m 2·℃/W 。
二、总传热系数K 的范围在设计换热器时,常需预知总传热系数K 值,此时往往先要作一估计。
总传热系数K 值主要受流体的性质、传热的操作条件及换热器类型的影响。
K 的变化范围也较大。
表4-5中列有几种常见换热情况下的总传热系数。
表4-5 常见列管换热器传热情况下的总传热系数K冷 流 体热 流 体K/(W ·m -2·℃-1)水 水 水 水 水 有机溶剂 水水 气体 有机溶剂 轻油 重油 有机溶剂 水蒸气冷凝850~1700 17~280 280~850 340~910 60~280 115~340 1420~4250气体 水 水沸腾 轻油沸腾水蒸气冷凝 低沸点烃类冷凝 水蒸气冷凝 水蒸气冷凝30~300 455~1140 2000~4250 455~1020三、提高总传热系数的途径传热过程的总热阻K 1是由各串联环节的热阻叠加而成,原则上减小任何环节的热阻都可提高传热系数。
但是,当各环节的热阻相差较大时,总热阻的数值将主要由其中的最大热阻所决定。
此时强化传热的关键在于提高该环节的传热系数。
例如,当管壁热阻和污垢热阻均可忽略时,式4-71可简化为 21111αα+=K若α1>>α2,则K 1≈21α,欲要提高K 值,关键在于提高对流传热系数较小一侧的α2。
若污垢热阻为控制因素,则必须设法减慢污垢形成速率或及时清除污垢。
【例4-7】 热空气在冷却管管外流过,α2=90W/(m 2·℃),冷却水在管内流过,α1=1000W/(m 2·℃)。
冷却管外径d o =16mm ,壁厚b =1.5mm ,管壁的λ=40W/(m ·℃)。
试求:①总传热系数K o ;②管外对流传热系数α2增加一倍,总传热系数有何变化? ③管内对流传热系数α1增加一倍,总传热系数有何变化? 解:①由式4-70可知 21111αλα++⋅=m o i o od d b d d K9015.1416400015.01316100011++=8.8001111.000004.000123.01=++=W/(m 2·℃)可见管壁热阻很小,通常可以忽略不计。
②()C m W/4147902100123012 ⋅=⨯+=..K o传热系数增加了82.4%。
③()C m W/385011110131610002112 ⋅=+⨯=..K o传热系数只增加了6%,说明要提高K 值,应提高较小的α2值。
4-5-4 传热推动力和总传热速率方程随着传热过程的进行,换热器各截面上冷热流体的温差(T -t )是不同的,因此若以Δt 表示整个传热面积的平均推动力,且K 为常量,则式4-66积分式为Q=KS Δt (4-72)上式称为总传热速率方程。
下面讨论不同情况下传热平均推动力的计算和总传热速率方程的表达式。
一、恒温传热换热器的间壁两侧流体均有相变化时,例如蒸发器中,饱和蒸气和沸腾液体间的传热就是恒温传热,此时,冷、热流体的温度均不沿管长变化,即Δt =T -t ,流体的流动方向对Δt 也无影响。
式4-72变为Q=KS (T -t )=KS Δt (4-73) 二、变温传热变温传热时,若两流体的相互流向不同,则对温度差的影响也不相同,故应予以分别讨论。
1.逆流和并流在换热器中,两流体若以相反的方向流动,称为逆流;若以相同的方向流动称为并流,如图4-21所示。
由图可见,温度差沿管长发生变化,故需求出平均温度差。
下面以逆流为例,推导计算平均温度差的通式。
由换热器的热量衡算微分式知d Q =-W h c ph d T =W c c pc d t (4-74)图4-21 变温传热时的温度差变化 图4-22 逆流时平均温度差的推导(a )逆流(b )并流在稳定连续传热情况下,W h 、W c 为常量,且认为c ph 、c pc 是常数,则 phh c W Q T d d =pcc c W Q td d =显然Q -T 和Q -t 都是直线关系,因此T -t =Δt 与Q 也呈直线关系,如图4-22所示。
由图4-22可以看出,Q -Δt 的直线斜率为 ()Qt t Qt 12d d ∆∆∆-=将式(4-66)代入上式可得 ()Q t t t S K t 12d d ∆∆∆∆-=式中K 为常量,积分上式,有()⎰⎰-=21012d d 1t t s S Q t t t t K ∆∆∆∆∆∆ 得 S Q t t t t K 1212ln 1∆∆∆∆-=mt KS t t t t KSQ ∆∆∆∆∆=-=1212ln (4-75)该式是传热计算的基本方程式。
Δt m 称为对数平均温度差,即1212ln t t t t t m ∆∆∆∆∆-=(4-76) 对并流情况,可导出同样公式。
在实际计算中一般取Δt 大者为Δt 2,小者为Δt 1。
当Δt 2/Δt 1<2时,可用算术平均温度差(Δt 2+Δt 1)/2代替Δt m 。
在换热器中,只有一种流体有温度变化时其并流和逆流时的平均温度差是相同的。