下载文档原格式
和差问题和差知两个数的和与两个数的差，求两个数各是多少的应用题。
为了解决这类应用题，首先要弄清两个数相差多少的不同叙述方式。
有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们把暗藏起来的差叫“暗差”。
和差问题的数量关系式是：（和—差）÷2=小数（和＋差）÷2=小数和—小数=大数小数+差=大数一、解法深度点拨解决和差问题常用的方法是假设法，即在解题的过程中，可以将其中的小数增加到与大数相同的大小，则可以先求出大数，再求出小数;也可以将其中的大数减少到与小数相同的大小，则可以先求出小数，再求出大数。
同时还可以结合线段图进行分析。
二、例题名师精解例1 两筐水果共重150千克，第二筐比第一筐多10千克，两筐水果各多少千克?题例赏析这是一道典型的有关和差问题的题，根据题意第二筐和第一筐的和是150千克，差是10千克，我们用线段图表示如下:根据上图可知，假设第一筐增加10千克，第一筐和第二筐的质量就一样了，即第一筐、第二筐质量之和加上差就是第二筐质量的2倍。
这样，我们就可以求出第二筐的质量。
思路点拨第二筐重多少千克? (150+10)÷2=80(千克)第一筐重多少千克? 150-80=70(千克)或80-10=70(千克) 同样假设第二筐减少10千克，第二筐就和第一筐的质量一样了，即第一筐、第二筐质量之和减去差就是第一筐质量的2倍。
这样我们就可以求出第一筐的质量。
第一筐重多少千克? (150-10)÷2=70(千克) 第二筐重多少千克? 150-70=80(千克)或70+10=80(千克) 视角延伸和差问题的解题关键在于使两个不相等的数进行变化，化为相等的两个数。
从本例中我们发现小数加上差等于大数，两倍的大数等于和加上差;大数减去差等于小数，两倍的小数等于和减差。
例2今年小强7岁，爸爸35岁，当两人年龄和是58岁时，两人年龄各多少岁?题例赏析题中没有给出小强和爸爸的年龄之差，但是已知两人今年的年龄，那么今年两人的年龄差是35-7=28(岁)。
专题2-和差问题小升初数学思维拓展典型应用题专项训练（知识梳理+典题精讲+专项训练）1、和差问题。
已知两个数量的和与差，求这两个数量各是多少，这类应用题叫和差问题。
2、计算公式。
（和+差）÷2=大数（和-差）÷2=小数．【典例一】甲、乙两数的平均数是18.4，甲比乙多4，则甲是（）A、20.4B、22.4C、16.4【分析】根据题意，甲、乙两数的平均数是18.4，那么它们的和是18.4×2=36.8，又甲比乙多4，也就是它们的差是4，然后再根据和差公式进一步解答．【解答】解：18.4×2=36.8；（36.8+4）÷2=20.4．答：甲是20.4．故选：A．【点评】根据题意，求出两个数的和与差，由和差公式进一步解答．【典例二】王宁和妈妈一起糊纸灯笼，共糊了80个。
如果妈妈给王宁12个纸灯笼后，两人糊灯笼的数量同样多。
妈妈和王宁各糊纸灯笼多少个？【分析】根据“妈妈给王宁12个纸灯笼后，两人糊灯笼的数量同样多”，可以推算出妈妈糊的灯笼比王宁多2个12，再根据和差问题的解题公式：（和-差）2÷=小数，求出王宁糊纸灯笼多少个，最后用两人糊的灯笼的总数减去王宁糊纸灯笼的个数，可以计算出妈妈糊纸灯笼的个数。
【解答】解：(80122)2-⨯÷=-÷(8024)2=÷562=（个)28-=（个)802852答：王宁糊纸灯笼28个，妈妈糊纸灯笼52个。
【点评】本题解题关键是找出题目中两种量的和与差各是多少，再根据和差问题的解题公式：（和-差）2÷=小数，列式计算。
【典例三】张星和王宁一共有邮票128张。
王宁给张星28张后，两人邮票张数同样多。
两人原来各有多少张邮票？（先画图表示题中的数量关系，再解答）【分析】根据题意画图即可，已知两人一共有邮票128张，王宁给张星28张后，两人邮票张数同样多，则现在每人有邮票128264+=（张)，张÷=（张)，则王宁原有邮票642892星原有邮票642836-=（张)【解答】解：128264÷=（张)王宁：642892+=（张)张星：642836-=（张)答：王宁原有邮票92张，张星原有邮票36张。
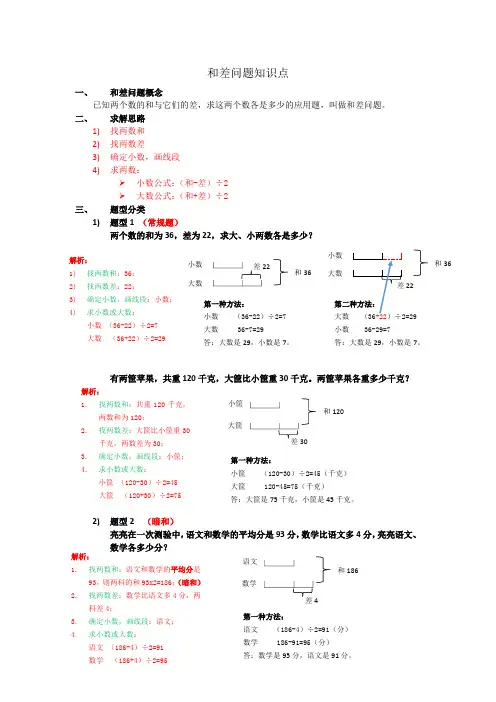
和差问题知识点一、 和差问题概念已知两个数的和与它们的差，求这两个数各是多少的应用题，叫做和差问题。
二、 求解思路1) 找两数和 2) 找两数差3) 确定小数，画线段 4) 求两数：➢ 小数公式：（和-差）÷2 ➢ 大数公式：（和+差）÷2三、 题型分类1) 题型1 （常规题）两个数的和为36，差为22，求大、小两数各是多少？有两筐苹果，共重120千克，大筐比小筐重30千克。
两筐苹果各重多少千克？2) 题型2 （暗和）亮亮在一次测验中，语文和数学的平均分是93分，数学比语文多4分，亮亮语文、数学各多少分？解析： 1) 找两数和：36； 2) 找两数差：22；3) 确定小数，画线段：小数； 4) 求小数或大数： 小数 （36-22）÷2=7 大数 （36+22）÷2=29小数 大数 和36 差22 第一种方法： 小数 （36-22）÷2=7 大数 36-7=29 答：大数是29，小数是7。
第二种方法： 大数 （36+22）÷2=29小数 36-29=7 答：大数是29，小数是7。
小数和36 大数 差22 解析： 1. 找两数和：共重120千克，两数和为120； 2. 找两数差：大筐比小筐重30千克，两数差为30； 3. 确定小数，画线段：小筐； 4. 求小数或大数： 小筐 （120-30）÷2=45 大筐 （120+30）÷2=75小筐 大筐差30 和120 第一种方法： 小筐 （120-30）÷2=45（千克）大筐 120-45=75（千克） 答：大筐是75千克，小筐是45千克。
解析：1. 找两数和：语文和数学的平均分是93，则两科的和93x2=186；（暗和）2. 找两数差：数学比语文多4分，两科差4；3. 确定小数，画线段：语文；4.求小数或大数： 语文 （186-4）÷2=91 数学 （186+4）÷2=95语文数学差4和186 第一种方法：语文 （186-4）÷2=91（分） 数学 186-91=95（分） 答：数学是95分，语文是91分。
和差问题重点讲解、难点突破与针对性训练已知两个数的和以及这两个数的差，求这两个数是多少的应用题，叫作和差问题．．．．.碰到这类问题，对小学生来说是有一定难度.特别是它的变型题，容易绕晕学生的头脑.在这里，我把和差问题模型化，总结出它们的解题思路，起到抛砖引玉的目的.并配备相应练习题进行针对性训练，提高解决和差问题的能力.基本题型例1两车皮水果共重180吨，一号车皮比二号车皮重20吨，两车皮水果分别有多少吨？解法一：一号车皮水果重是（180+20）÷2=100（吨）二号车皮水果重100-20=80（吨）解法二：二号车皮水果重（180-20）÷2=80（吨）一号车皮水果重是80+20=100（吨）答：两车皮水果重量分别有100、80吨.【解题总结】【针对性训练】1．王红家饲养了50鸡，母鸡比公鸡多12只.王红家养母鸡、公鸡分别多少只？2、某校学农基地种植桃树和梨树共有61棵，其中桃树比梨树多9棵，这个学农基地有桃树、梨树多少棵？3、植树节，红卫中学初一、初二年级学生共植树156棵，初二年级比初一年级多植树34棵，初一、初二年级分别植树多少棵？变型题Ⅰ例22020年小明13岁，爸爸43岁，当两人年龄和是68岁时，两人年龄各多少岁？解：2020年小强13岁，爸爸43岁，爸爸比小明大30岁（两人年龄差永远不变．．．．．．．．．），当两人年龄和是68岁时，爸爸年龄是（68+30）÷2=49（岁），而小明的年龄是49-30=19（岁）.答:爸爸年龄是49岁，小明的年龄是19岁.【解题总结】第一步：只明确给出两数之和，未明确给出两数之差，先求两数之差；第二步：套用两数和差模型解题思路计算.【针对性训练】4、王明今年有8岁，张帆今年14岁，当两人的年龄和是48岁时，两人的年龄各是几岁？5、张东今年12岁，妈妈39岁，当两人年龄和是63岁时，两人年龄各多少岁？6、小明期终考试，语文和数学的平均分数是97分，语文比数学少6分，语文和数学各得了几分？变型题Ⅱ例3红红一部书有上、中、下三册，上册比中册贵1元，中册比下册贵2元，这部书售价32元.上、中、下三册各多少元？解法一：上册比中册贵1元，中册比下册贵2元，所以上册比下册贵3元，而上、中、下三册32元，那么上册售价是（32+1+3）÷3=12（元），而中册售价12-1=11（元），而下册售价（12-3）元=9元.解法二：上册比中册贵1元，中册比下册贵2元，所以上册比下册贵3元，而上、中、下三册32元，那么下册售价是（32-2-3）÷3=9（元），而中册售价9+2=11（元），而下册售价（9+3）元=12元.答:上、中、下三册各是12、11、9元.【解题总结】【注意】“法一”中“（差1+差2）”就是“甲-丙=差1+差2”，如果设甲-丙=差3，那么甲=（和+差1+差3）÷3.【针对性训练】7、A、B、C三个数的和为300，已知A比B大50，B比C大20，甲数是多少？8、学校有合唱队、电脑绘画班、英语学习班共有学生130人，其中合唱队比电脑绘画班多20人，英语学习班比电脑绘画班少10人，他们分别是多少人？9、六年级三个班共植树420棵，一班比二班多植树10棵，二班比三班少植树17棵，三个班各植树多少棵？变型题Ⅲ例4甲、乙两筐香蕉共64千克，如果从甲筐里取5千克放到乙筐里去，结果甲筐的香蕉还比乙筐的香蕉多2千克.甲、乙两筐原有香蕉各多少千克？解：从甲筐里取5千克放到乙筐里去，结果甲筐的香蕉还比乙筐的香蕉多2千克，已知甲、乙两筐香蕉共64千克.那么现在甲框有香蕉（64+2）÷2=33（千克），而现在乙框有香蕉33-2=31（千克）.因此原来甲框有香蕉（33+5）=38（千克），乙框有香蕉（31-5）=26（千克）.答：甲、乙两筐原有香蕉各38、26千克.【解题总结】涉及物品移动、数字补偿问题，分现在和过去两个状态.先用两数和差模型计算现在，再计算原来，还原回去.【针对性训练】10、两筐苹果共重64千克，如果从第一筐中取出8千克放入第二筐后，那么，第一筐苹果比第二筐少2千克.两筐苹果原来各有多少千克？11、甲、乙两个工程队共有1980人，甲队为了支援乙队，抽出285人加入乙队，这时乙队人数还比甲队少24人，求甲、乙两队原有工人多少人？12、甲、乙两校共有学生864人，如果照顾学生就近入学，从甲校调入乙校32名同学，这样甲校学生还比乙校多48人，问甲、乙两校原来各有学生多少人？【针对性训练】答案解析基本题型1、解：母鸡是（50+12）÷2=31（只），而公鸡是31-12=19（只）.答:母鸡是31只，公鸡是19只.2、解：桃树是（61+9）÷2=35（颗），而梨树是35-9=26（颗）.答:桃树是35颗，梨树是26颗.3、解：初二年级植树（156+34）÷2=95（颗），而初一年级植树是95-34=61（颗）答:初二年级植树95颗，初一年级植树是61颗.变型题Ⅰ4、解：王明今年有8岁，张帆今年14岁，所以张帆比王明大6岁，当两人年龄和是48岁时，那么张帆年龄是（48+6）÷2=27（岁），而王明的年龄是27-6=21（岁）.答:张帆年龄是27岁，王明的年龄是21岁.5、解：张东今年12岁，妈妈39岁，所以妈妈比张东大27岁，当两人年龄和是63岁时，那么妈妈年龄是（63+27）÷2=45（岁），而张东的年龄是45-27=18（岁）.答:妈妈年龄是45岁，张东的年龄是18岁.6、解：数学比语文多6分，两科分数和是97×2=194，数学是（194+6）÷2=100（分），而语文的年龄是100-6=94（分）.答:语文94分，数学100分.变型题Ⅱ7、解：已知A比B大50，B比C大20，所以A数比C数大70，A、B、C三个数的和为300，那么A是（300+50+70）÷3=140，而B是140-50=90，而C是140-70=70.答:A、B、C三个数各是140、90、70.8、解：合唱队比电脑绘画班多20人，英语学习班比电脑绘画班少10人，所以合唱队比英语学习班30人.合唱队、电脑绘画班、英语学习班共有学生130人，那么合唱队有（130+20+30）÷3=60，而电脑绘画班是60-20=40（人），而英语学习班60-30=30.答：他们分别是60、40、30人.9、解：已知一班比二班多植树10棵，二班比三班少植树17棵，三个班共植树420棵，那么二班植树（420-10-17）÷3=131（棵），而一班植树131+10=141（棵），而三班植树131+17=148（棵）.答：一、二、三班分别植树141、131、148棵.变型题Ⅲ10、解：从第一筐里取8千克放到第二筐里去，结果第一筐的苹果比第二筐的苹果少2千克，两筐苹果共重64千克.那么现在第二框有苹果（64+2）÷2=33（千克），而现在第一框有苹果33-2=31（千克）.因此原来第一框有苹果（31+8）=39（千克），第二框有苹果（33-8）=25（千克）.答：第一、二筐原有苹果各39、25千克.11、解：从甲队抽调285人加入乙队，乙队人数还比甲队少24人，而甲、乙两个工程队共有1980人.那么现在甲队有（1980+24）÷2=1002（人），而现在乙队有1002-24=978（人）.因此原来甲队有（1002+285）=1287（人），乙队有（978-285）=693（人）.答：甲队、乙队原有苹果各1287、693人.12、解：从甲校调入乙校32名同学，甲校学生还比乙校多48人，而甲、乙两校共有学生864人.那么现在甲校有（864+48）÷2=456名学生，而乙校有（456-48）=408名学生，因此甲校原有456+32=488名学生，而乙校有（408-32）=376名学生.答：甲、乙两校原有学生是488、376名.。
典型应用题四和差问题————————————————————————————————作者：————————————————————————————————日期：23 / 5(四)和差问题概念及类型：已知大、小两个数的和，以及它们的差，求这两个数各是多少的应用题，叫做和差问题。
解题关键：解这类题的关键是把大、小两个数的和转化成两个大数的和(或两个小数的和)，然后再求另一个数。
解题规律：(和+差)÷2=大数大数-差=小数(和-差)÷2=小数和-小数=大数例1.一根线绳和一根麻绳总长为48米，已知线绳比麻绳长10米，求线绳和麻绳各长多少米？分析：如图3－4－1所示，两绳总长是48米，减去线绳比麻绳长的那一段(10米)，正好是麻绳长度的2倍。
(48-10=38)，除以2就得出麻绳长度。
然后，再去求线绳的长度。
(48-10)÷2=19(米)48-19=29(米)答：线绳长29米，麻绳长19米。
例2.甲、乙两仓库共存货物988吨，如果从甲仓库调22吨货物到乙仓库，那么，甲、乙两仓库货物同样多。
问原来两仓库各存货多少吨？分析：如图3－4－2所示，从甲仓库调出22吨货物放入乙仓库，这时两仓库货物相等，那么，在调动22吨货物之前，甲仓库比乙仓库多22×2=44吨，这样又可以按和差问题的规律去解题了。
4 / 5解：(988-22×2)÷2=472(吨)(988+22×2)÷2=516(吨)答：原来甲仓库存货物516吨，乙仓库存货物472吨。
例3.某农民种玉米、谷子和棉花共148公亩，种的玉米比谷子多21公亩，种的棉花比玉米少32公亩，三种作物各种了多少公亩？分析：如图3－4－3所示，玉米比谷子多21公亩，而比棉花多32公亩。
为了便于分析，可以把三种作物转化成同样多，也就是把玉米、谷子都转化成和棉花同样多的公亩数。
[148-32-(32-21)]这样就形成三个棉花的公亩数。
奥数精讲-和差问题1.和差问题的意义：已知大小两个数的和及它们的差，求这两个数各是多少的应用题，叫作和差应用题，简称和差问题。
2.和差问题的解题规律：解答和差问题通常用假设法，同时还可以结合线段图进行分析，解题时可以假设小数增加到与大数同样多，先求大数，再求小数；也可以假设大数减少到与小数同样多，先求小数，再求大数。
3.和差问题的解题方法：小数加上两数差就是大数，两数和加上两数差便是大数的2倍；大数减去两数差就是小数，两数和减去两数差是小数点的2倍。
因此，用两数和加上两数差，再除以2，就可以求出其中的大数；用两数和减去两数差，再除以2，就可求出小数。
4.和差数量关系公式：大数=（和+差）÷2；小数=（和-差）÷2冲关例题1：参加运动会的六年级学生共有326人，其中女生比男生多24人。
六年级男、女生各有多少人参加运动会？解: （326－24）÷2＝151（人）151＋24＝175（人）或（326＋24）÷2＝175（人）175－24＝151（人）答：六年级男生有151人，女生有175人参加运动会。
冲关例题2：兰兰和花花共有68元钱，如果兰兰给花花5元，则两人的钱数一样多。
原来两人各有多少钱？解：（68＋5×2）÷2＝39（元）（68－10）÷2＝29（元）或68－39＝29（元）或39－10＝29（元）答：原来兰兰有39元钱，花花有29元钱。
冲关例题3：一个三层的书架共放了100本书，第二层比第一层多放了16本，第三层比第一层少放了18本。
这三层书架各放了多少本书？解：（100－16＋18）÷3＝34（本）34＋16＝50（本）34－18＝16（本）答：第一层放了34本书，第二层放了50本书，第三层放了16本书。
和差问题一、复习旧知1、所谓和差问题，一般是指知道两个数的和与两个数的差，分别求出这两个数的应用题。
这两个数一个大些，称之为大数，一个小些，称之为小数。
例如：小玲期末考试语文、数学总成绩是194分，数学比语文高6分，小玲的语文、数学成绩各是多少分？这个应用题是已知两个数（语文、数学）的和（194分）与差（6分），求这两个数的问题。
大数=（和+差）÷2 小数=（和-差）÷2根据以上的关系式，我们可以正确解答这类应用题。
二、新课讲解例1、甲、乙两筐苹果共重90千克，从甲筐取出8千克放入乙筐，甲筐比乙筐还多4千克，甲、乙两筐原来各有苹果多少千克？例2、学校四、五、六年级共植树120棵，四年级比五年级少植8棵，六年级比五年级多植8棵，三个年级各植树多少棵？三、课堂练习1、某校二年级有学生106人，分成了两个班。
如果一班调2个学生到二班去，两个班学生人数就相等。
原来一班和二班各有学生多少人？2、小明期中考试语、数、英三门总分是270分，语文比数学少10分，英语比数学少5分，小明三门各考多少分？四、过关检测1、甲、乙两个数的和是70，甲比乙哦16，甲、乙各是多少？2、长方形的周长是84厘米，长比宽多8厘米，长方形的面积是多少平方厘米？3、学校进行体检活动，小明和小刚共重70千克，小刚和小海共重80千克，小海和小明共重66千克，小明、小刚、小海各重多少千克？4、兄弟两人共有人民币50元，哥哥给弟弟8元后，还比弟弟多2元，哥哥和弟弟原来各有多少钱？五、家庭作业1、小明期末考试时语文和数学的平均分是94分，数学比语文多8分，问语文和数学各得多少分？2、甲乙两校共有学生864人，为了照顾学生就近入学，从甲校调入乙校32名同学，这样甲校学生还比乙校多48人，问甲、乙两校原来各有多少人？3、有三块布料一共190米，第二块比第一块长20米第三块比第二块长30米，每块布料各长多少米？。
和差问题【专题简析】已知两数的和及它们的差，求求这两个数各是多少，这类问题我们称为“和差问题”。
掌握了和差问题的特征和规律，我们解答起来就很方便了。
解答和差问题通常用假设法，同时结合线段图进行分析。
可以假设较小数增加到与较大数同样多，先求较大数，再求较小数；也可以假设较大数减少到与较小数同样多，先求较小数，再求较大数。
用数量关系式表示：（和＋差）÷2=较大数（和－差）÷2=较小数【例题精讲】例1. 期末考试王平和李阳语文成绩总和为188分，李阳比王平少4分，两人各考了多少分？例2. 哥弟两共有邮票70张，如果哥哥给弟弟4张邮票后还比弟弟多2张，问哥哥和弟弟原来各有邮票多少张？例3. 三年前爸爸年龄是女儿的4倍，爸爸今年43岁，女儿今年多少岁？例4. 4年前，妈妈的年龄是女儿的3倍，4年后，母女年龄和是56岁，妈妈今年多少岁？例5. 爸爸今年45岁，他有三个儿子，大儿子15岁，二儿子11岁，三儿子7岁，要过多少年爸爸的岁数等于他三个儿子的岁数和？【当堂检测】1．两筐水果共重124千克，第一筐比第二筐多8千克，两筐水果各重多少千克？2．一只两层书架共放书72本，若从上层中拿出9本给下层，上层还比下层多4本，上、下层各放书多少本？3．4年前小林年龄是小丽的2倍，小林今年12岁，小丽今年多少岁？4．3年前，哥哥的年龄是弟弟的2倍，3年后，哥弟两的年龄和是30岁，哥哥今年多少岁？5．今年姐姐20岁，哥哥18岁，弟弟12岁，妹妹8岁，几年后，姐姐、哥哥年龄和的2倍等于弟弟、妹妹年龄和的3倍？【课后作业】1．小宁与小慧的身高总和是264厘米，又已知小宁比小慧矮8厘米，两人身高分别多少厘米？2．姐姐和妹妹共有糖果39块，如果姐姐给妹妹7块后就比妹妹少3块，那么姐姐和妹妹原来各有糖果多少块？3．5年前爷爷年龄是孙子的7倍，孙子今年14岁，爷爷今年多少岁？4．5年前，小明的年龄是小红的3倍，5年后，小明和小红年龄和是44岁，今年小明多少岁？5．爷爷今年80岁，他有三个孙子，大孙子30岁，二孙子25岁，小孙子17岁，要过几年爷爷的岁数等于他三个孙子岁数和？。
和差问题(经典)知识点1：和差问题公式和差应用题是指已知两个数的和与差，求出这两个数各是多少。
解答这类问题需要用到以下公式：①（和－差）÷2=小数②小数＋差=大数和－小数=大数或：①（和＋差）÷2=大数②大数－差=小数和－大数=小数解答和差应用题的关键是选择适当的数作为标准，设法把若干个不相等的数变为相等的数。
对于某些复杂的应用题，如果没有直接告诉我们两个数的和与差，可以通过转化求它们的和与差，再按照和差问题的解法来解答。
知识点2：题目类型1、已知和与差的具体数据。
2、已知和，未知差（暗差），需要求出差。
3、已知和，未知差（暗差），但是稍微复杂。
4、已知差，未知和。
需要求出和。
5、已知和，涉及三个量的问题。
例1：三、四年级同学共植树128棵，四年级比三年级多植树20棵，求三、四年级同学各植树多少棵？解答：根据公式①和②，可以列出以下方程组：①（x+y）÷2=y-20②x+y=128通过解方程，可以得到：三年级：（128-20）÷2=54（棵）四年级：（128+20）÷2=74（棵）因此，三年级同学植树54棵，四年级同学植树74棵。
例2：两筐梨子共有120个，如果从第一筐中拿10个放到第二筐中，那么两筐的梨子个数相等。
两筐原来各有多少个梨？解答：根据公式①和②，可以列出以下方程组：①（x+y）÷2=x-10②x+y=120通过解方程，可以得到：第一筐：（120+20）÷2=70（个）第二筐：（120-20）÷2=50（个）因此，第一筐有70个梨，第二筐有50个梨。
练1：XXX四（1）班和四（2）班共有学生108人，从四（1）班转3人到四（2）班，则两班人数同样多。
两个班原来各有学生多少人？练2：某汽车公司两个车队共有汽车80辆，如果从第一车队调10辆到第二车队，两个车队的汽车辆数就相等。
两个车队原来各有汽车多少辆？乙仓库有大米371袋，甲仓库有大米429袋。
和差问题含义：已知大小两个数的和，以及它们的差，求这两个数各是多少，这样的问题叫做和差问题。
数量关系：（和＋差）÷2=大数和－大数=小数（和－差）÷2=小数和－小数=大数和差问题类型一：基本型【例1】三、四年级同学共植树128棵，四年级比三年级多植树20棵，求三、四年级同学各植树多少棵？解题思路1：已知三、四年级的和是128，差是20，四年级植树棵树是大数，三年级植树棵树是小数，直接利用公式求解。
列式：四年级（128+20）÷2=74（棵）三年级（128-20）÷2=54（棵）或 128-74=54（棵）答：三年级植树54棵，四年级植树74棵。
解题思路2：画线段图分析由图可知，若四年级去掉20棵之后则会变得跟三年级一样多，此时总数也得去掉20棵，再除以2就得到三年级的棵树。
反之若三年级加上20棵之后就会变得跟三年级一样多，此时总数也得加上20棵，再除以2就得到四年级的棵树。
列式：三年级（128-20）÷2=54（棵）四年级 128-54=74（棵）或（128-20）÷2=54（棵）答：三年级植树54棵，四年级植树74棵。
【例2】学校有排球和足球共60个，排球比足球多4个。
学校有排球和足球各多少个？解题思路1：已知排球、足球的和是60，差是4，排球的个数是大数，足球的个数是小数，直接利用公式求解。
列式：排球（60+4）÷2=32（个）足球（60-4）÷2=28（个）或 60-32=28（个）答：排球有32个，足球有28个。
解题思路2：画线段图分析由图可知，若排球去掉4个之后则会变得跟足球一样多，此时总数也得去掉4个，再除以2就得到足球的个数。
反之若足球加上4个之后就会变得跟排球一样多，此时总数也得加上4个，再除以2就得到排球的个数。
列式：排球（60+4）÷2=32（个）足球（60-4）÷2=28（个）或 60-32=28（个）答：排球有32个，足球有28个。
