当前位置：文档之家 › 黄庆明-模式识别与机器学习-第三章-作业

黄庆明-模式识别与机器学习-第三章-作业

  • 格式：doc
  • 大小：225.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

模式识别(3-1)

模式识别(3-1)

§3.2 最大似然估计
最大似然估计量： －使似然函数达到最大值的参数向量。 －最符合已有的观测样本集的那一个参数向量。 ∵学习样本从总体样本集中独立抽取的
N ) p( X | ) p( X k | i ) k 1 N个学习样本出现概率的乘积
i
i
∴
p( X | i . i
i
§3.2 Bayes学习
假定： ①待估参数θ是随机的未知量 ②按类别把样本分成M类X1，X2，X3，… XM 其中第i类的样本共N个 Xi = {X1,X2,… XN} 并且是从总体中独立抽取的 ③ 类条件概率密度具有某种确定的函数形式，但其 参数向量未知。 ④ Xi 中的样本不包含待估计参数θj(i≠j)的信息，不 同类别的参数在函数上是独立的，所以可以对每一 类样本独立进行处理。


有时上式是多解的, 上图有5个解,只有一个解最大即 （对所有的可能解进行检查或计算二阶导数）
§3.2 最大似然估计
例：假设随机变量x服从均匀分布，但参数1， 2未知， 1 1 x 2 p ( x | ) 2 1 ， 0 其他 求1， 2的最大似然估计量。 解：设从总体中独立抽取N个样本x1 , x2 , , xN , 则其似然函数为： 1 p ( x1 , x2 , , xN | 1， 2 ) ( 2 1 ) N l ( ) p ( X | ) 0




§3.2 Bayes学习
p ~ N 0 , 0

2

其中 0和 0 是已知的
2
已知的信息还包括一组抽取出来的样本X i x1 , x2 ,, xN ，从而 可以得到关于 的后验概率密度：

模式识别作业题(2)

模式识别作业题(2)
得证。 3、使用最小最大损失判决规则的错分概率是最小吗？为什么？
答：不是最小的。首先要明确当我们谈到最小最大损失判决规则时，先验概率是未知的， 而先验概率的变化会导致错分概率变化， 故错分概率也是一个变量。 使用最小最大损 失判决规则的目的就是保证在先验概率任意变化导致错分概率变化时， 错分概率的最 坏（即最大）情况在所有判决规则中是最好的（即最小）。 4、 若 λ11 = λ22 =0， λ12 = λ21 ，证明此时最小最大决策面是来自两类的错误率相等。 证明：最小最大决策面满足 （ λ11 - λ22 ）+（ λ21 - λ11 ） 容易得到
λ11 P(ω1 | x) + λ12 P(ω2 | x) < λ21 P(ω1 | x) + λ22 P(ω2 | x) ( λ21 - λ11 ) P (ω1 | x) >( λ12 - λ22 ) P (ω2 | x) ( λ21 - λ11 ) P (ω1 ) P ( x | ω1 ) >( λ12 - λ22 ) P (ω2 ) P ( x | ω2 ) p( x | ω1 ) (λ 12 − λ 22) P(ω2 ) > 即 p( x | ω2 ) ( λ 21 − λ 11) P (ω1 )
6、设总体分布密度为 N( μ ，1)，-∞< μ <+∞,并设 X={ x1 ， x2 ，… xN }，分别用最大似然 估计和贝叶斯估计计算 μ 。已知 μ 的先验分布 p（ μ ）～N（0,1）。 解：似然函数为：
∧Байду номын сангаас
L（ μ ）=lnp(X|u)=
∑ ln p( xi | u) = −
i =1
N
模式识别第三章作业及其解答

模式识别与机器学习第一章

模式识别与机器学习第一章

结构模式识别
• 该方法通过考虑识别对象的各部分之间的联 系来达到识别分类的目的。
• 识别采用结构匹配的形式，通过计算一个匹 配程度值（matching score）来评估一个未知 的对象或未知对象某些部分与某种典型模式 的关系如何。
• 当成功地制定出了一组可以描述对象部分之 间关系的规则后，可以应用一种特殊的结构 模式识别方法 – 句法模式识别，来检查一个 模式基元的序列是否遵守某种规则，即句法 规则或语法。
• 图像处理 • 计算机视觉 • 人工智能 • 数据挖掘 • 控制论
……
教学方法
• 着重讲述模式识别与机器学习的基本概 念，基本理论和方法、关键算法原理以 及典型应用情况。
• 注重理论与实践紧密结合
–实例教学：通过实例讲述如何将所学知识 运用到实际应用之中
• 尽量避免引用过多的、繁琐的数学推导。
ቤተ መጻሕፍቲ ባይዱ
教学目标
Applications, Springer, New York, USA, 2002. • Christopher M. Bishop (2006)，Pattern Recognition and Machine
Learning，Springer. • Trevor Hastie, Robert Tibshirani, and Jerome Friedman (2001)，The
期。研究的是以40年代兴起的神经网络模型为理论基础的“没
有知识”的学习。模式识别发展的同时形成了机器学习的两种 重要方法：判别函数法和进化学习
• 第二阶段是在60年代中叶至70年代中叶，被称为机器 学习的冷静时期。研究的目标是模拟人类的概念学习阶段，
并采用逻辑结构或图结构作为机器内部描述。神经网络学习机 因理论缺陷转入低潮。

模式识别课后习题答案

模式识别课后习题答案

• 2.16 证明M ahalanobis距离r符合距离定义三定理，即 – (1) r(a, b) = r(b, a) – (2) 当且仅当a = b时，r(a, b) = 0 – (3) r(a, c) ≤ r(a, b) + r(b, c) 证明： (1) r(a, b) = (a − b)T Σ−1 (a − b) = (b − a)T Σ−1 (b − a) = r(b, a) (2) Σ为半正定矩阵所以r(a, b) = (a − b)T Σ−1 (a − b) ≥ 0，只有当a = b时，才有r(a, b) = 0。 (3) Σ−1 可对角化，Σ−1 = P ΛP T • 2.17 若将Σ−1 矩阵写为：Σ−1 h1d h2d ，证明M ahalanobis距离平方为 . . . hdd
• 2.13 把连续情况的最小错误率贝叶斯决策推广到离散情况，并写出其判别函数。 • 2.14 写出离散情况条件风险R(ai |x)的定义，并指出其决策规则。 解： R(ai |x) = = R(ak |x) = min
c ∑ j =1 c ∑ j =1
λij P (wj |x) λij pቤተ መጻሕፍቲ ባይዱx|wj )P (wj )////omit the same part p(x)
j =1,...,c j =1,...,c
考虑两类问题的分类决策面为：P (w1 |x) = P (w2 |x)，与p(x|w1 )P (w1 ) = p(x|w2 )P (w2 ) 是相同的。 • 2.9 写出两类和多类情况下最小风险贝叶斯决策判别函数和决策面方程。 • 2.10 随机变量l(x)定义为l(x) = p(x|w1 ) ，l(x)又称为似然比，试证明 p(x|w2 )
1

模式识别与机器学习 作业 中科院 国科大 来源网络 (3)

模式识别与机器学习 作业 中科院 国科大 来源网络 (3)

{ double sum=0.0; for(int j=0;j<T;j++) sum+=a[j]*C[j][i]; res[i]=sum; } } int main() { int T; int w1_num,w2_num; double w1[10][5],w2[10][5],m1[5]={0},m2[5]={0},C1[5][5]={0},C2[5][5]={0}; cin>>T>>w1_num>>w2_num; for(int i=0;i<w1_num;i++) { for(int j=0;j<T;j++) { cin>>w1[i][j]; m1[j]+=w1[i][j]; } } for(int i=0;i<w2_num;i++) { for(int j=0;j<T;j++) { cin>>w2[i][j]; m2[j]+=w2[i][j]; } } for(int i=0;i<w1_num;i++) m1[i]=m1[i]/w1_num; for(int i=0;i<w2_num;i++) m2[i]=m2[i]/w2_num; for(int i=0;i<w1_num;i++) { double res[5][5],a[5]; for(int j=0;j<T;j++) a[j]=w1[i][j]-m1[j]; get_matrix(T,res,a); for(int j=0;j<T;j++) { for(int k=0;k<T;k++) C1[j][k]+=res[j][k]; }

黄庆明 模式识别与机器学习 第三章 作业

黄庆明 模式识别与机器学习 第三章 作业
T d1(7)= w1 (7) x①=(-1 -1 -1)(-1 -1 1) =1
T
d2(7)= w2 (7) x①=(0 0 0)(-1 -1 1) =0
T
T
d3(7)= w3 (7) x①=(2 2 -2)(-1 -1 1) =-6
T
T
因 d1(7)>d2(7)，d1(7)>d3(7)，分类结果正确，故权向量不变。 由于第五、六、七次迭代中 x①、x②、x③均已正确分类，所以权向量的解为： T w1=(-1 -1 -1) T w2=(0 0 0) T w3=(2 2 -2) 三个判别函数： d1(x)=- x1 -x2-1 d2(x)=0 d3(x)=2x1+2x2-2
·采用梯度法和准则函数
J ( w, x, b)
1 8x
2
[( wT x b) wT x b ]2
式中实数 b>0，试导出两类模式的分类算法。
J 1 ( wT x b) | wT x b | * x - x * sign(wT x b) 2 w 4 ｜ | x ||
用二次埃尔米特多项式的势函数算法求解以下模式的分类问题 ω1: {(0 1)T, (0 -1)T} ω2: {(1 0)T, (-1 0)T} （1）
1 ( x) 1 ( x1 , x2 ) H 0 ( x1 ) H 0 ( x2 ) 1 2 ( x) 2 ( x1 , x2 ) H 0 ( x1 ) H1 ( x2 ) 2 x2 3 ( x) 3 ( x1 , x2 ) H 0 ( x1 ) H 2 ( x2 ) 4 x22 2 4 ( x) 4 ( x1 , x2 ) H1 ( x1 ) H 0 ( x2 ) 2 x1 5 ( x) 5 ( x1 , x2 ) H1 ( x1 ) H1 ( x2 ) 4 x1 x2 6 ( x) 6 ( x1 , x2 ) H1 ( x1 ) H 2 ( x2 ) 2 x1 (4 x22 2) 7 ( x) 7 ( x1 , x2 ) H 2 ( x1 ) H 0 ( x2 ) 4 x12 2 8 ( x) 8 ( x1 , x2 ) H 2 ( x1 ) H1 ( x2 ) 2 x2 (4 x12 2) 9 ( x) 9 ( x1 , x2 ) H 2 ( x1 ) H 2 ( x2 ) (4 x12 2)(4 x22 2)

模式识别第三章

模式识别第三章

3 回归的线性模型至此，本书都聚焦在无监督学习，包括的议题有密度估计和数据聚类。

我们现在转向监督学习，并从回归开始。

回归的目的是：对给定的输入变量的D 维向量x 值，预测一个或更多连续目标变量t 值。

我们在第一章考虑多项式曲线拟合时，已经遇到过一个回归问题的例子。

多项式是线性回归模型的一大类函数中一个具体的例子，它也有含可调参数的线性函数的性质，并将组成本章的焦点。

最简单的线性回归模型也是输入变量的线性函数。

但是，通过取输入变量的一组给定的非线性函数的线性组合，我们可以获得更有用的函数类，称为基函数。

这样的模型是参数的线性函数，它们有简单的解析性，并且关于输入变量仍是非线性的。

给定一个训练数据集合，它有N 个观察值{}n x ，其中n=1,…,N ，以及对应的目标值{}n t ，目的是给定一个新的x 预测t 的值。

最简单方法是直接构造一个适当的函数()y x ，对一个新输入x ，它的值组成对应的t 的预测值。

更一般地，从概率角度考虑，我们想建立一个预测分布()p t x ，因为它表示了对x 的每一个值，t 值的不确定性。

由这个条件分布，我们可以为任意的新x 值预测t ，这相当于最小化一个适当选择的损失函数的期望。

如在第1.5.5所讨论的，通常选择损失函数的平方作为实值变量的损失函数，因为它的最优解由t 的条件期望给出。

对模式识别来说，虽然线性模型作为实用的技术有显著的限制，特别是涉及到高维输入空间的问题，但是它们具有好的解析性质，并且是以后章节要讨论的更复杂模型的基础。

3.1 线性基函数模型最简单的线性回归模型是输入变量的线性组合：011(,)D D y w w x w x =+++x w L （3.1） 其中1(,,)T D x x =x L ，这就是通常简称的线性回归。

此模型的关键特征是：它是参数0,,D w w L 的一个线性函数。

但同时它也是输入变量i x 的一个线性函数，这对模型产生了很大的限制。

模式识别Chapter 3归纳.ppt

模式识别Chapter 3归纳.ppt

最新.课件
11
Discriminant functions
yk (x)
1 2
(x
k
)
t
k
1
(
x
k )
d 2
ln
2
1 2
ln
| k
| ln
p(ck )
Case 1 k 2I
yk
(x)
1
2
k t
x
kt k
ln
p(ck
)
yk (x) wkt x wk0
wk
1
2
k , wk 0
ktk
最新.课件
21
Introduction
we could design an optional classifier if we knew the priori probabilities and the class-conditional densities
Unfortunately, we rarely, if ever, have this kind of completely knowledge about the probabilistic structure
Feature space, feature point in space
Classification
-- Bayesian decision theory
-- Discriminant function
-- Decision region, Decision boundary
最新.课件
15
Example
Drawbacks -- the number of parameters grows with the size of the data -- slow

模式识别与机器学习思考题及参考答案

模式识别与机器学习思考题及参考答案

模式识别与机器学习期末考查思考题1:简述模式识别与机器学习研究的共同问题和各自的研究侧重点。

机器学习是研究让机器(计算机)从经验和数据获得知识或提高自身能力的科学。

机器学习和模式识别是分别从计算机科学和工程的角度发展起来的。

然而近年来,由于它们关心的很多共同问题(分类、聚类、特征选择、信息融合等),这两个领域的界限越来越模糊。

机器学习和模式识别的理论和方法可用来解决很多机器感知和信息处理的问题,其中包括图像/视频分析、(文本、语音、印刷、手写)文档分析、信息检索和网络搜索等。

近年来,机器学习和模式识别的研究吸引了越来越多的研究者,理论和方法的进步促进了工程应用中识别性能的明显提高。

机器学习:要使计算机具有知识一般有两种方法;一种是由知识工程师将有关的知识归纳、整理,并且表示为计算机可以接受、处理的方式输入计算机。

另一种是使计算机本身有获得知识的能力,它可以学习人类已有的知识,并且在实践过程中不总结、完善,这种方式称为机器学习。

机器学习的研究,主要在以下三个方面进行:一是研究人类学习的机理、人脑思维的过程;和机器学习的方法;以及建立针对具体任务的学习系统。

机器学习的研究是在信息科学、脑科学、神经心理学、逻辑学、模糊数学等多种学科基础上的。

依赖于这些学科而共同发展。

目前已经取得很大的进展,但还没有能完全解决问题。

模式识别:模式识别是研究如何使机器具有感知能力,主要研究视觉模式和听觉模式的识别。

如识别物体、地形、图像、字体(如签字)等。

在日常生活各方面以及军事上都有广大的用途。

近年来迅速发展起来应用模糊数学模式、人工神经网络模式的方法逐渐取代传统的用统计模式和结构模式的识别方法。

特别神经网络方法在模式识别中取得较大进展。

理解自然语言计算机如能“听懂”人的语言(如汉语、英语等),便可以直接用口语操作计算机,这将给人们带来极大的便利。

计算机理解自然语言的研究有以下三个目标:一是计算机能正确理解人类的自然语言输入的信息,并能正确答复(或响应)输入的信息。

《模式识别与机器学习》习题和参考答案

《模式识别与机器学习》习题和参考答案

性函数。上式可以看作对 x 的各分量进行线性组合，然后平移，所以 r (x) 服从一
维高斯分布。下面计算一维高斯分布 p(r (x) | w 1) 的期望 m1 和方差 1 ：
m1 [r (x) | w 1]
1
(μ 2 μ1 ) 1μ1 (μ1 1μ1 μ 2 1μ 2 )
190%
(2-13)
最小风险贝叶斯决策会选择条件风险最小的类别，即 h( x) 1 。
3.
给出在两类类别先验概率相等情况下，类条件概率分布是相等对角协方差
矩阵的高斯分布的贝叶斯决策规则，并进行错误率分析。
答：
（1）首先给出决策面的表达式。根据类条件概率分布的高斯假设，可以
得到
p(x | w i )
1/2
2 |
p(C, M ) p(C | M ) p(M ) 0.2 0.6 0.12
p( M | C )
p(C | M ) p( M )
0.12

0.25
p(C | M ) p( M ) p(C | F ) p( F ) 0.12 0.36
(2-1)
(2-2)
2. 举例说明最小风险贝叶斯决策与最小错误率贝叶斯决策的不同。
R(h( x) 1| x)
(h( x) 1| w 1) p( w 1| x) (h( x) 1| w 2) p( w 2 | x)
98.1%
(2-12)
R ( h( x ) 2 | x )
(h( x) 2 | w 1) p( w 1| x) (h( x) 2 | w 2) p( w 2 | x)
(2-16)

模式识别(山东联盟)知到章节答案智慧树2023年青岛大学

模式识别(山东联盟)知到章节答案智慧树2023年青岛大学

模式识别（山东联盟）知到章节测试答案智慧树2023年最新青岛大学第一章测试1.关于监督模式识别与非监督模式识别的描述正确的是参考答案:非监督模式识别对样本的分类结果是唯一的2.基于数据的方法适用于特征和类别关系不明确的情况参考答案:对3.下列关于模式识别的说法中,正确的是参考答案:模式可以看作对象的组成成分或影响因素间存在的规律性关系4.在模式识别中，样本的特征构成特征空间，特征数量越多越有利于分类参考答案:错5.在监督模式识别中，分类器的形式越复杂，对未知样本的分类精度就越高参考答案:错第二章测试1.下列关于最小风险的贝叶斯决策的说法中正确的有参考答案:最小风险的贝叶斯决策考虑到了不同的错误率所造成的不同损失;最小错误率的贝叶斯决策是最小风险的贝叶斯决策的特例;条件风险反映了对于一个样本x采用某种决策时所带来的损失2.我们在对某一模式x进行分类判别决策时，只需要算出它属于各类的条件风险就可以进行决策了。

参考答案:对3.下面关于贝叶斯分类器的说法中错误的是参考答案:贝叶斯分类器中的判别函数的形式是唯一的4.当各类的协方差矩阵相等时，分类面为超平面，并且与两类的中心连线垂直。

参考答案:错5.当各类的协方差矩阵不等时，决策面是超二次曲面。

参考答案:对第三章测试1.概率密度函数的估计的本质是根据训练数据来估计概率密度函数的形式和参数。

参考答案:对2.参数估计是已知概率密度的形式，而参数未知。

参考答案:对3.概率密度函数的参数估计需要一定数量的训练样本，样本越多，参数估计的结果越准确。

参考答案:对4.下面关于最大似然估计的说法中正确的是参考答案:最大似然估计是在已知概率密度函数的形式，但是参数未知的情况下，利用训练样本来估计未知参数。

;在最大似然估计中要求各个样本必须是独立抽取的。

;在最大似然函数估计中，要估计的参数是一个确定的量。

5.贝叶斯估计中是将未知的参数本身也看作一个随机变量，要做的是根据观测数据对参数的分布进行估计。

中科院_黄庆明_模式识别_考试试卷总结_国科大

中科院_黄庆明_模式识别_考试试卷总结_国科大

的

k j
来计算：
kh
w
hj
k j
j
因此，算出
kh
后，

k h
也就求出了。
如果前面还有隐蔽层，用

k h
再按上述方法计算
kl
和

k l
，以此类
推，一直将输出误差δ一层一层推算到第一隐蔽层为止。各层的δ
求得后，各层的加权调节量即可按上述公式求得。由于误差

k j
相当
于由输出向输入反向传播，所以这种训练算法成为误差反传算法
第四步：返回第二步，重复计算及合并，直到得到满意的分类结
果。（如：达到所需的聚类数目，或 D(n)中的最小分量超过给定阈值
D 等。）
聚类准则函数
（1）最短距离法：设 H 和 K 是两个聚类，则两类间的最短距离定义
为：
DH,K min{ d u,v}, u H, v K 其中，du,v 表示 H 类中的样本 xu 和 K 类中的样本 xv 之间的距离， DH,K 表示 H 类中的所有样本和 K 类中的所有样本之间的最小距 离。
k j

y
k j
)
2

1 2
{T
k j
k, j
F[
h
whj F (
i
wih xik )]}2
为了使误差函数最小，用梯度下降法求得最优的加权，权值先从
输出层开始修正，然后依次修正前层权值，因此含有反传的含义。
根据梯度下降法，由隐蔽层到输出层的连接的加权调节量为：
w
hj


E w hj
模式试卷总结
一、 模式
1.什么是模式：广义地说，存在于时间和空间中可观察的物体，如果我们可以区 别它们是否相同或是否相似，都可以称之为模式。 模式所指的不是事物本身，而是从事物获得的信息，因此，模式往往表现为具有 时间和空间分布的信息。 2.模式的直观特性：可观察性、可区分性、相似性 3.模式识别的分类：监督学习、概念驱动或归纳假说；非监督学习、数据驱动或 演绎假说。 4.模式分类的主要方法：数据聚类、统计分类、结构模式识别、神经网络。

模式识别与机器学习_作业_中科院_国科大_来源网络（4）

模式识别与机器学习_作业_中科院_国科大_来源网络（4）

模式识别与机器学习_作业_中科院_国科大_来源网络（4）第5章作业：作业一：设有如下三类模式样本集ω1，ω2和ω3，其先验概率相等，求S w 和S bω1：{(1 0)T , (2 0) T , (1 1) T } ω2：{(-1 0)T , (0 1) T , (-1 1) T } ω3：{(-1 -1)T , (0 -1) T , (0 -2) T }答案：由于三类样本集的先验概率相等，则概率均为1/3。

多类情况的类内散布矩阵，可写成各类的类内散布矩阵的先验概率的加权和，即：∑∑===--=cii i Ti i cii w C m x m x E P S 11}|))(({)(ωω 其中C i 是第i 类的协方差矩阵。

其中1m = 4313,2m =2323,3m =1343则=++=321S w w w w S S S 1/32/31/3?1/32/3 +1/3 2/31/31/32/3+ 1/3 2/3?1/3?1/32/3 = 2/3?1/9?1/92/3类间散布矩阵常写成：Ti i ci i b m m m m P S ))(()(001--=∑=ω其中，m 0为多类模式（如共有c 类）分布的总体均值向量，即：c i m P x E m i cii i ,,2,1,,)(}{10 =?==∑=ωω0m =1/3 13?13 = 19?19则Ti i cii b m m m m P S ))(()(001--=∑=ω=13 1.49380.54320.54320.1975 +13 0.6049?0.6049?0.60490.6049 +13 0.19750.54320.5432 1.4938 = 0.76540.16050.16050.7654作业二：设有如下两类样本集，其出现的概率相等：ω1：{(0 0 0)T , (1 0 0) T ,(1 0 1) T , (1 1 0) T }ω2：{(0 0 1)T , (0 1 0) T ,(0 1 1) T , (1 1 1) T }用K-L 变换，分别把特征空间维数降到二维和一维，并画出样本在该空间中的位置。

模式识别作业第三章2

模式识别作业第三章2

第三章作业已知两类训练样本为1:(0 0 0 )',(1 0 0)' ,(1 0 1)',(1 1 0)'ω2:(0 0 1)',(0 1 1)' ,(0 1 0)',(1 1 1)'ω设0)'(-1,-2,-2,)1(=W,用感知器算法求解判别函数，并绘出判别界面。

$解：matlab程序如下：clear%感知器算法求解判别函数x1=[0 0 0]';x2=[1 0 0]';x3=[1 0 1]';x4=[1 1 0]';x5=[0 0 1]';x6=[0 1 1]';x7=[0 1 0]';x8=[1 1 1]';%构成增广向量形式，并进行规范化处理[x=[0 1 1 1 0 0 0 -1;0 0 0 1 0 -1 -1 -1;0 0 1 0 -1 -1 0 -1;1 1 1 1 -1 -1 -1 -1];plot3(x1(1),x1(2),x1(3),'ro',x2(1),x2(2),x2(3),'ro',x3(1),x3(2),x3(3),'ro',x4(1),x4(2),x4(3),'ro');hold on; plot3(x5(1),x5(2),x5(3),'rx',x6(1),x6(2),x6(3),'rx',x7(1),x7(2),x7(3),'rx',x8(1),x8(2),x8(3),'rx');grid on; w=[-1,-2,-2,0]';c=1;N=2000;for k=1:N|t=[];for i=1:8d=w'*x(:,i);if d>0w=w;、t=[t 1];elsew=w+c*x(:,i);t=[t -1];end-endif i==8&t==ones(1,8)w=wsyms x yz=-w(1)/w(3)*x-w(2)/w(3)*y-1/w(3);《ezmesh(x,y,z,[ 1 2]);axis([,,,,,]);title('感知器算法')break;else{endend运行结果：w =3]-2-31判别界面如下图所示：!若有样本123[,,]'x x x x =;其增广]1,,,[321x x x X =;则判别函数可写成： 1323')(321+*-*-*=*=x x x X w X d若0)(>X d ,则1ω∈x ，否则2ω∈x已知三类问题的训练样本为123:(-1 -1)', (0 0)' , :(1 1)'ωωω<试用多类感知器算法求解判别函数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

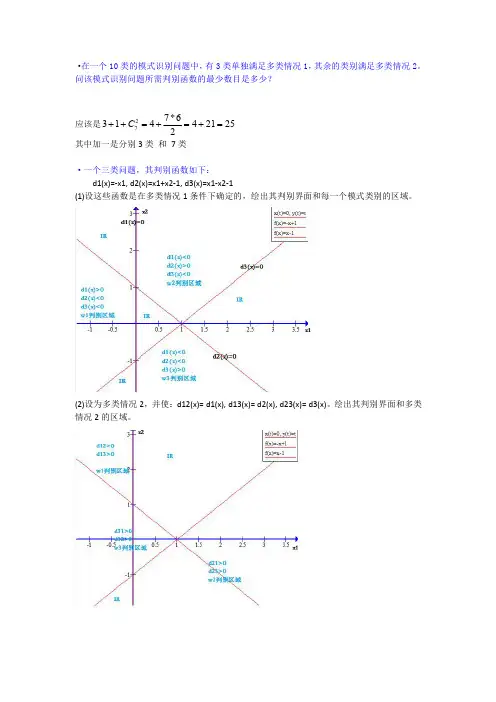
·在一个10类的模式识别问题中，有3类单独满足多类情况1，其余的类别满足多类情况2。

问该模式识别问题所需判别函数的最少数目是多少？应该是2521426*741327=+=+=++C 其中加一是分别3类 和 7类·一个三类问题，其判别函数如下： d1(x)=-x1, d2(x)=x1+x2-1, d3(x)=x1-x2-1(1)设这些函数是在多类情况1条件下确定的，绘出其判别界面和每一个模式类别的区域。

(2)设为多类情况2，并使：d12(x)= d1(x), d13(x)= d2(x), d23(x)= d3(x)。

绘出其判别界面和多类情况2的区域。

(3)设d1(x), d2(x)和d3(x)是在多类情况3的条件下确定的，绘出其判别界面和每类的区域。

·两类模式，每类包括5个3维不同的模式，且良好分布。

如果它们是线性可分的，问权向量至少需要几个系数分量？假如要建立二次的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变。

） 如果线性可分，则4个建立二次的多项式判别函数，则1025 C 个·(1)用感知器算法求下列模式分类的解向量w: ω1: {(0 0 0)T , (1 0 0)T , (1 0 1)T , (1 1 0)T } ω2: {(0 0 1)T , (0 1 1)T , (0 1 0)T , (1 1 1)T }将属于ω2的训练样本乘以（-1），并写成增广向量的形式。

x ①=(0 0 0 1)T , x ②=(1 0 0 1)T , x ③=(1 0 1 1)T , x ④=(1 1 0 1)Tx ⑤=(0 0 -1 -1)T , x ⑥=(0 -1 -1 -1)T , x ⑦=(0 -1 0 -1)T , x ⑧=(-1 -1 -1 -1)T第一轮迭代：取C=1，w(1)=(0 0 0 0) T因w T (1) x ① =(0 0 0 0)(0 0 0 1) T=0 ≯0，故w(2)=w(1)+ x ① =(0 0 0 1)因w T (2) x ② =(0 0 0 1)(1 0 0 1) T =1>0，故w(3)=w(2)=(0 0 0 1)T因w T (3)x ③=(0 0 0 1)(1 0 1 1)T =1>0，故w(4)=w(3) =(0 0 0 1)T因w T (4)x ④=(0 0 0 1)(1 1 0 1)T =1>0，故w(5)=w(4)=(0 0 0 1)T因w T (5)x ⑤=(0 0 0 1)(0 0 -1 -1)T =-1≯0，故w(6)=w(5)+ x ⑤=(0 0 -1 0)T因w T (6)x ⑥=(0 0 -1 0)(0 -1 -1 -1)T =1>0，故w(7)=w(6)=(0 0 -1 0)T因w T (7)x ⑦=(0 0 -1 0)(0 -1 0 -1)T =0≯0，故w(8)=w(7)+ x ⑦=(0 -1 -1 -1)T因w T (8)x ⑧=(0 -1 -1 -1)(-1 -1 -1 -1)T =3>0，故w(9)=w(8) =(0 -1 -1 -1)T因为只有对全部模式都能正确判别的权向量才是正确的解，因此需进行第二轮迭代。

第二轮迭代：因w T (9)x ①=(0 -1 -1 -1)(0 0 0 1)T =-1≯0，故w(10)=w(9)+ x ① =(0 -1 -1 0)T因w T (10)x ②=(0 -1 -1 0)( 1 0 0 1)T =0≯0，故w(11)=w(10)+ x ② =(1 -1 -1 1)T因w T (11)x ③=(1 -1 -1 1)( 1 0 1 1)T =1>0，故w(12)=w(11) =(1 -1 -1 1)T因w T (12)x ④=(1 -1 -1 1)( 1 1 0 1)T =1>0，故w(13)=w(12) =(1 -1 -1 1)T因w T (13)x ⑤=(1 -1 -1 1)(0 0 -1 -1)T =0≯0，故w(14)=w(13)+ x ⑤ =(1 -1 -2 0)T因w T (14)x ⑥=(1 -1 -2 0)( 0 -1 -1 -1)T =3>0，故w(15)=w(14) =(1 -1 -2 0)T因w T (15)x ⑧=(1 -1 -2 0)( 0 -1 0 -1)T =1>0，故w(16)=w(15) =(1 -1 -2 0)T因w T (16)x ⑦=(1 -1 -2 0)( -1 -1 -1 -1)T =2>0，故w(17)=w(16) =(1 -1 -2 0)T因为只有对全部模式都能正确判别的权向量才是正确的解，因此需进行第三轮迭代。

第三轮迭代：w(25)=(2 -2 -2 0);因为只有对全部模式都能正确判别的权向量才是正确的解，因此需进行第四轮迭代。

第四轮迭代：w(33)=(2 -2 -2 1)因为只有对全部模式都能正确判别的权向量才是正确的解，因此需进行第五轮迭代。

第五轮迭代：w(41)=(2 -2 -2 1)因为该轮迭代的权向量对全部模式都能正确判别。

所以权向量即为(2 -2 -2 1),相应的判别函数为123()2221d x x x x =--+(2)编写求解上述问题的感知器算法程序。

见附件·用多类感知器算法求下列模式的判别函数： ω1: (-1 -1)T ω2: (0 0)T ω3: (1 1)T 将模式样本写成增广形式：x ①=(-1 -1 1)T , x ②=(0 0 1)T , x ③=(1 1 1)T取初始值w 1(1)=w 2(1)=w 3(1)=(0 0 0)T，C=1。

第一轮迭代（k=1）：以x ①=(-1 -1 1)T作为训练样本。

d 1(1)=)1(1Tw x ①=(0 0 0)(-1 -1 1)T=0d 2(1)=)1(2Tw x ①=(0 0 0)(-1 -1 1)T=0d 3(1)=)1(3T w x ①=(0 0 0)(-1 -1 1)T=0因d 1(1)≯d 2(1)，d 1(1)≯d 3(1)，故w 1(2)=w 1(1)+x ①=(-1 -1 1)Tw 2(2)=w 2(1)-x ①=(1 1 -1)Tw 3(2)=w 3(1)-x ①=(1 1 -1)T第二轮迭代（k=2）：以x ②=(0 0 1)T作为训练样本d 1(2)=)2(1Tw x ②=(-1 -1 1)(0 0 1)T=12d 3(2)=)2(3Tw x ②=(1 1 -1)(0 0 1)T=-1因d 2(2)≯d 1(2)，d 2(2)≯d 3(2)，故w 1(3)=w 1(2)-x ②=(-1 -1 0)Tw 2(3)=w 2(2)+x ②=(1 1 0)Tw 3(3)=w 3(2)-x ②=(1 1 -2)T第三轮迭代（k=3）：以x ③=(1 1 1)T作为训练样本d 1(3)=)3(1Tw x ③=(-1 -1 0)(1 1 1)T=-2d 2(3)=)3(2Tw x ③=(1 1 0)(1 1 1)T=2d 3(3)=)3(3T w x ③=(1 1 -2)(1 1 1)T=0因d 3(3)≯d 2(3)，故w 1(4)=w 1(3) =(-1 -1 0)Tw 2(4)=w 2(3)-x ③=(0 0 -1)Tw 3(4)=w 3(3)+x ③=(2 2 -1)T第四轮迭代（k=4）：以x ①=(-1 -1 1)T作为训练样本d 1(4)=)4(1Tw x ①=(-1 -1 0)(-1 -1 1)T=2d 2(4)=)4(2Tw x ①=(0 0 -1)(-1 -1 1)T=-1d 3(4)=)4(3T w x ①=(2 2 -1)(-1 -1 1)T=-5因d 1(4)>d 2(4)，d 1(4)>d 3(4)，故w 1(5)=w 1(4) =(-1 -1 0)Tw 2(5)=w 2(4) =(0 0 -1)Tw 3(5)=w 3(4) =(2 2 -1)T第五轮迭代（k=5）：以x ②=(0 0 1)T作为训练样本d 1(5)=)5(1Tw x ②=(-1 -1 0)(0 0 1)T=0d 2(5)=)5(2Tw x ②=(0 0 -1)(0 0 1)T=-1d 3(5)=)5(3Tw x ②=(2 2 -1)(0 0 1)T=-1因d 2(5) ≯d 1(5)，d 2(5) ≯d 3(5)，故w 1(6)=w 1(5)-x ② =(-1 -1 -1)w 2(6)=w 2(5)+x ②=(0 0 0) w 3(6)=w 3(5)-x ②=(2 2 -2)第六轮迭代（k=6）：以x ③=(1 1 1)T作为训练样本d 1(6)=)6(1Tw x ③=(-1 -1 -1)(1 1 1)T=-32d 3(6)=)6(3Tw x ③=(2 2 -2)(1 1 1)T=2因d 3(6)>d 1(6)，d 3(6)>d 2(6)，故w 1(7)=w 1(6)w 2(7)=w 2(6) w 3(7)=w 3(6)第七轮迭代（k=7）：以x ①=(-1 -1 1)T作为训练样本d 1(7)=)7(1Tw x ①=(-1 -1 -1)(-1 -1 1)T=1d 2(7)=)7(2Tw x ①=(0 0 0)(-1 -1 1)T=0d 3(7)=)7(3Tw x ①=(2 2 -2)(-1 -1 1)T =-6因d 1(7)>d 2(7)，d 1(7)>d 3(7)，分类结果正确，故权向量不变。

由于第五、六、七次迭代中x ①、x ②、x ③均已正确分类，所以权向量的解为：w 1=(-1 -1 -1)Tw 2=(0 0 0)Tw 3=(2 2 -2)T三个判别函数：d 1(x)=- x 1 -x 2-1 d 2(x)=0d 3(x)=2x 1+2x 2-2·采用梯度法和准则函数22])[(81),,(b x w b x w xb x w J T T ---=式中实数b>0，试导出两类模式的分类算法。

[][])sign(*x -x *||)(|||412b x w b x w b x w x w J TT T ----=∂∂｜其中，⎩⎨⎧≤-->+=-010-1)(b x w if b x w if b x w sign TT T当0>-b x w T 时，则w(k+1) = w(k)，此时不对权向量进行修正；当0≤-b x w T 时，则)(|||)()1(2b x w x Cx k w k w k Tk k k -+=+｜，需对权向量进行校正，初始权向量w(1)的值可任选。