长方体和正方体整理复习

长方体和正方体整理与复习
请说说长方体和正方体的表面积、 体积、棱长和公式
棱长和=（长+宽+高）×4 表面积=(长×宽+长×高+宽×高) ×2 S =（ab+ah+bh）×2
体 积=长×宽×高
棱长和V ==棱ab长h×12 表面积=棱长×棱长×6
S=6a2 体 积=棱长×棱长×棱长
V=a3
6厘米
8厘米
的正方形，长2m，50根这样的方木一共是 多少立方米？合多少立方分米？ （6）王叔叔要粉刷一个长7.5m,7m,高3.6m 的教室的墙壁（天花板不刷），已知门窗 面积为5.5m2 ,求应粉刷的面积。
白云居课件
7、要把8盒果汁装一箱，果汁盒的长是8cm， 宽是5cm，高是20cm。请你设计 一个包装箱。怎样包装所用的包装纸最少？
）。
白云居课件
5、我能填得对
(1)6.2dm 3=( )cm 3 560cm =3( )dm 3
(2)3.9L=( )ML 0.6m=( )dm
(3)4cm=( )m
2.5dm2 =( 2)cm2
(4)960dm2 =( )m2 1.2m3 =( )dm3
白云居课件
6、解决问题
（1）将一个苹果放进一个长20cm、宽15cm 的长方体容器中，在向容器中注水，使苹 果完全浸没，然后把它取出，这时水面下 降了5cm。这个苹果的体积是多少？
锯成棱长1dm的小正方体，可以锯（ ）个。 ①18 ②180 ③90
（4）一个长方体的棱长的和是36cm，它的长、宽、 高的和是（ ）cm。 ①12 ②9 ③6
（5）至少需要（ ）个同样的小正方体，才可以 一个稍大的正方体。 ①1 ②4 ③8
（6）将一个正方体钢块锻造成长方体，正方体和长 方体（ ）。①体积相等，表面积不相等

解:设水深大约x厘米。
40升＝40000立方厘米
（50× 40）x＝40000
x＝40000÷ 2000
x＝20
答：水深大约20厘米。
把一个棱长0.8米的正方体钢坯，锻造成一 个横截面面积是0.16平方米的长方体方钢。 锻造成的这块方钢长多少米？
0.8×0.8×0.8÷0.16＝3.2（米）
用包装纸把两个长6厘米，宽5厘米，高4厘米的长方 体礼盒包在一起，有几种包法，哪种包装方法最节 省材料？
长方体和正方体 的整理与复习
形
相同点
体 面 棱 顶点
面的形状
不同点 面的面积
棱长
长 方 体
6 个 面
12 条 棱
8 个 顶 点
6个面都是长方形， 有时有两个相对的 相对面的面积相等
面是正方形
相对应的 棱的长度 相等
8
正 6 12 个 方个 条 顶 体面 棱 点
6个面的面积都想等
6个面都是完全相同 的正方形
6、相邻的面是正方形的长方体是正方体。 （ √ ）
一件雕塑的底座是用混凝土浇注成的棱长2.6米 的正方体。（只列式不计算 ）
1.这件雕塑占地多少平方米？ 2.6×2.6＝6.76(m2)
2. 浇注这件雕塑底座需要混凝土多少立方米？
2.6×2.6×2.6=17.576(m3）
3. 给这件雕塑的底座四周贴上花岗石，贴花岗 石的面积是多少平方米？2.6×2.6×4=243;bh)
面积×长 米
叫做它们 ×2 的表面积。
平方分 米
V=abh
立方 米
容器所能容纳物
正 方 体
正方体表面积＝ 棱长×棱长×6
平方米
体的体积，叫做 正方体体 这个容器的容积。积＝棱长

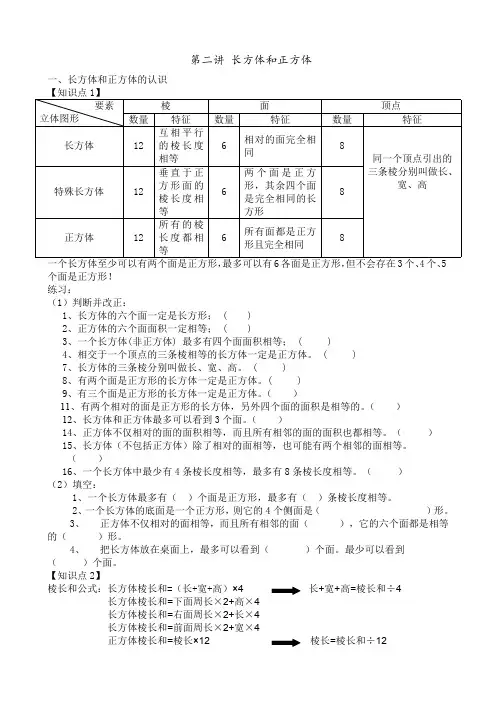
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形，其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形，最多可以有6各面是正方形，但不会存在3个、4个、5个面是正方形！练习：（1）判断并改正：1、长方体的六个面一定是长方形； ( )2、正方体的六个面面积一定相等； ( )3、一个长方体(非正方体) 最多有四个面面积相等； ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。

( )7、长方体的三条棱分别叫做长、宽、高。

( )8、有两个面是正方形的长方体一定是正方体。

( )9、有三个面是正方形的长方体一定是正方体。

（ ）11、有两个相对的面是正方形的长方体，另外四个面的面积是相等的。

（ ）12、长方体和正方体最多可以看到3个面。

（ ） 14、正方体不仅相对的面的面积相等，而且所有相邻的面的面积也都相等。

（ ） 15、长方体（不包括正方体）除了相对的面相等，也可能有两个相邻的面相等。

（ ）16、一个长方体中最少有4条棱长度相等，最多有8条棱长度相等。

（ ）（2）填空：1、一个长方体最多有（ ）个面是正方形，最多有（ ）条棱长度相等。

2、一个长方体的底面是一个正方形，则它的4个侧面是（ ）形。

3、正方体不仅相对的面相等，而且所有相邻的面（ ），它的六个面都是相等的（ ）形。

4、把长方体放在桌面上，最多可以看到（ ）个面。

最少可以看到（ ）个面。

【知识点2】棱长和公式：长方体棱长和=（长+宽+高）长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形：例如：有一个礼盒需要用彩带捆扎，捆扎效果如图，打结部分需要10厘米彩带，一共需要多长的彩带？分析：本题虽然并未直接提出求棱长和，但由于彩带的捆扎是和棱相互平行的， 因此，在解决问题时首先确定每部分彩带与那条棱平行，从而间接去求棱长和。

结论: 结论
只有容器才能有容积， 只有容器才能有容积，如 果是实心的木块等， 果是实心的木块等，是不会 有容积的。 有容积的。
3.计量容积，一般用体积单位。 计量容积，一般用体积单位。 计量容积 体积单位
若计量液体的体积，如药水、 若计量液体的体积，如药水、 汽油等，常用容积单位升 毫升。 汽油等，常用容积单位升和毫升。
填空： 填空：
3、正方体有（ 6 ）个面、（12） 、正方体有（ 个面、（ 条棱、（ 个顶点。 条棱、（ 8 ）个顶点。 4、长方体（ 相对的 ）面相等， 、长方体（ 面相等， 正方体（ 个 面相等。 正方体（ 6个 ）面相等。
平行的4条 平行的 条 棱长度相 5、长方体（ 、长方体（ ） 正方体（ 条 棱长度相等。 等，正方体（ 12条 ）棱长度相等。
1.根据图中的数据填空。（口答） 根据图中的数据填空。（口答） 根据图中的数据填空。（口答 （1）如图1，这是_______体，它的长 是_____厘米，宽是____厘米，高是 ____厘米。12条棱长的和是____厘米。 (10+4+7)×4=84（厘米） （2）图2是一个长方体，长、宽、高分 别是9厘米，3厘米，4.5厘米。它上面的 面长是_____厘米，宽____厘米，右面 的长____厘米，宽____厘米，相交于一 个顶点的三条棱长和是____厘米。 （3）如图3，这是______体，它的棱长是 ___厘米。12条棱长的和是___厘米。
图3 图1
10厘米
７厘米
图2 4厘米 4厘米
判断（对的在括号里打“ 判断（对的在括号里打“√”，错误的打“×” ） 错误的打“ 正方体和长方体都是6个面、12条棱 条棱、 个顶点。 ①正方体和长方体都是6个面、12条棱、8个顶点。 ( ) √ 正方体的6个面一定是正方形。 ②正方体的6个面一定是正方形。 √ ( ) 正方体是特殊的长方体。 ③正方体是特殊的长方体。 ( ) √ 个长方体中如果有2个面是正方形， ④1个长方体中如果有2个面是正方形，那么这个 长方体一定是正方体。 长方体一定是正方体。( × ) 个长方体中如果相邻的2个面都是正方形， ⑤1个长方体中如果相邻的2个面都是正方形，那 么这个长方体一定是正方体。 么这个长方体一定是正方体。 ( ) √

小学数学苏教版六年级上册《长方体和正方体整理与复习》教案一. 教材分析《长方体和正方体整理与复习》是人教版小学数学六年级上册的一章内容。

这一章节主要让学生复习和整理之前学过的长方体和正方体的知识，包括它们的特征、表面积和体积的计算方法等。

通过本章的学习，学生可以加深对长方体和正方体的理解，提高解决问题的能力。

二. 学情分析六年级的学生已经在前面的学习中接触过长方体和正方体的知识，对它们的基本特征和计算方法有一定的了解。

但是，由于时间的推移，学生可能对这些知识有所遗忘，需要通过复习和整理来巩固。

此外，学生的学习能力和数学思维能力各有差异，需要在教学过程中给予不同的关注和指导。

三. 教学目标1.让学生掌握长方体和正方体的特征，能够准确地识别它们。

2.让学生熟练掌握长方体和正方体的表面积和体积的计算方法，能够灵活运用这些方法解决实际问题。

3.培养学生的空间想象能力和逻辑思维能力，提高解决问题的能力。

四. 教学重难点1.重点：长方体和正方体的特征，表面积和体积的计算方法。

2.难点：灵活运用长方体和正方体的知识解决实际问题。

五. 教学方法采用问题驱动法、案例分析法、小组合作法等教学方法，引导学生主动探究、合作交流，通过实践操作和思考，巩固和提高长方体和正方体的知识。

六. 教学准备1.PPT课件：包括长方体和正方体的特征、表面积和体积的计算方法的示例和练习题。

2.练习题：包括选择题、填空题、解答题等不同类型的题目，用于巩固和拓展学生的知识。

3.教学工具：直尺、三角板、剪刀、胶水等，用于学生的实践操作。

七. 教学过程导入（5分钟）通过一个生活实例引入长方体和正方体的概念，例如：“请大家观察一下我们教室的桌子，它是一个什么形状的物体？”引导学生回答：“长方体。

”通过这样的问题，激发学生的兴趣，引出本节课的主题。

呈现（10分钟）1.利用PPT课件，呈现长方体和正方体的特征，包括它们的定义、性质和相互关系。

2.利用PPT课件，呈现长方体和正方体的表面积和体积的计算方法，包括公式和计算步骤。

-可编辑修改-长方体和正方体的知识整理、【概念】等，有12条棱，每条棱的长度都相等长方体的棱长总和=（长+宽+高）X 4【长方体和正方体的表面积】1、长方体或正方体6个面和总面积叫做它的表面积长方体的表面积=（长X 宽+长X 高+宽X 高）X 2S=2 （ab + ah + bh ） 正方体的表面积=棱长X 棱长X 6 S=a X a X6= 6a 22、表面积的常用单位有： 平方米、平方分米、平方厘米相邻两个面积单位 之间的进率是 100 1m 2 =100dm 2 1 dm 2 =100 cm 2 1m 2 =10000 cm 2三、【长方体和正方体的体积】1、体积：物体所占空间的大小叫做物体的体积姓名（ ） 1、长方体或正方体两个面相交的边叫做 棱。

三条棱相交的点叫做顶点。

相交于 一个顶点的三条棱的长度分别叫做长方体的 长、宽、高2、正方体是长、宽、高都相等的长方体，它是一种 特殊的长方体3、长方体有6个面，8个顶点，12条棱，相对的面的面积相等，相对的棱的 长度相等。

一个长方体 最多有6个面是长方形，最少有4个面是长方形，最多 有2个面是正方形。

正方体有 6个面 ，每个面都是 止力形 ，每个面的 面积都相正方体的棱长总和=棱长X 12 正方体的棱长=棱长总和* 12-可编辑修改-2、 常用的体积单位有： 立方米（m 3）、 立方分米（dm 3）、立方厘 米（cm 3 ）① 棱长是1 cm 的正方体，体积是1 cm 3② 棱长是1 dm 的正方体，体积是1 dm 3③ 棱长是1 m 的正方体，体积是1 m 3 相邻两个体积单位之间的进率是 1000 1 m 3 =1000 dm 3 1dm 3=1000 cm 31 m 3 =1000000cm 3 长方体的体积=长x 宽x 高 V=abh 长方体（正方体）的体积=底面积x 高V =S xh 正方体的体积=棱长x 棱长x 棱长 v=a x a x a =a 3（a 3读作“ a 的立方” 表示3个a 相乘，即a a a ）3、 容积：容器所能容纳物体的体积，叫做它的容积。

5、体积单位间的进率都是1000 。 （×） 6、把一个正方体的橡皮泥捏成一个长方体后 虽然它的形状变了，但是它所占的空间大小不 变。（√ ）
7、正方体的棱长扩大2倍，它的体积就扩大6 倍。（× ）
2、学以致用
①做这样一个饮料包装 盒至少需要多少平方厘 米硬纸板？(接头不计)
9×3×2+9×12×2+3×12×2
12厘米 =54+216+72
=342（平方厘米）
9厘米
3厘米
2、学以致用
②这盒酸酸乳的容 积是多少毫升？
12厘米
9×3×12 =324（立方厘米） =324毫升
9厘米
3厘米
小结合小 整设理计的师概念,说一说下列问题实际要求什么?
（1）做这个鱼缸要用多少分米的角钢？
6×4+3×4+4×4 =24+12+16 =52（分米）
4.6升 = ( 4600 ) 毫升
9.5立方分米= (9.5 ) 升
7.6平方米=（ 7 ）平方米（ 60 ）平方分米
7.6平方米 =（760 ）平方分米=（76000）平方厘米
仔细斟酌，我最拿手！
1一个木箱的体积就是它的容积 （ ×） 2、长方体是特殊的正方体。 （× ） 3、棱长6分米的正方体，它的表面积和体积相等。 （× ） 4、用4个棱长1厘米的小正方体可以拼成一个大 正方体。（ × ）
3、一根长方体木料长2米，横截面是周长8厘米的正方形， 这根木料的体积是多少?
2米=200厘米
8÷4=2（厘米）
2×2×200=800（立方厘米）
拓展题： 难度系数：
（1）把一根长30厘米的长方体木料锯成3段(如 图),表面积比本来增加了20平方厘米,这根木料本 来的体积是多少立方厘米?

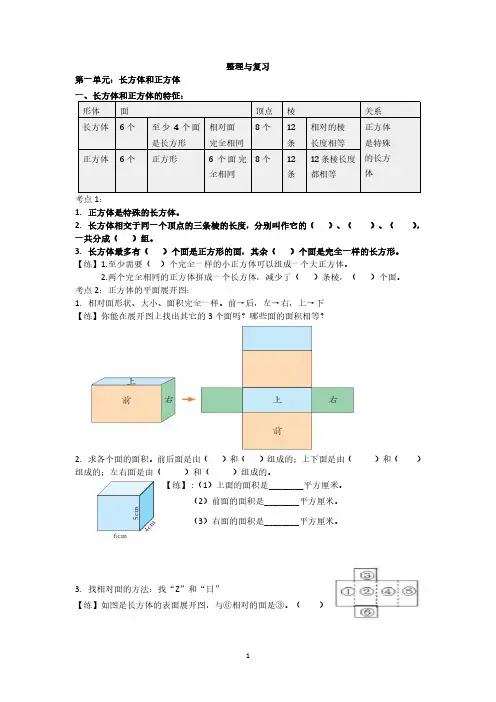
整理与复习第一单元：长方体和正方体一、长方体和正方体的特征：形体面顶点棱关系长方体6个至少4个面是长方形相对面完全相同8个12条相对的棱长度相等正方体是特殊的长方体正方体6个正方形6个面完全相同8个12条12条棱长度都相等考点1：1.正方体是特殊的长方体。

2.长方体相交于同一个顶点的三条棱的长度，分别叫作它的（）、（）、（），一共分成（）组。

3.长方体最多有（）个面是正方形的面，其余（）个面是完全一样的长方形。

【练】1.至少需要（）个完全一样的小正方体可以组成一个大正方体。

2.两个完全相同的正方体拼成一个长方体，减少了（）条棱，（）个面。

考点2：正方体的平面展开图：1.相对面形状、大小、面积完全一样。

前→后，左→右，上→下【练】你能在展开图上找出其它的3个面吗？哪些面的面积相等？2.求各个面的面积。

前后面是由（）和（）组成的；上下面是由（）和（）组成的；左右面是由（）和（）组成的。

【练】:（1）上面的面积是________平方厘米。

（2）前面的面积是________平方厘米。

（3）右面的面积是________平方厘米。

3.找相对面的方法：找“Z”和“日”【练】如图是长方体的表面展开图，与⑥相对的面是③。

（）如图是一个正方体的展开图，相对两个面上数字之和为0，则a+c=（）。

4.判断是否是正方体平面展开图的方法：无凸也无凹，没有大直角，没有田字格。

【练】：如图不是正方体的表面展开图。

（）5.哪几个面可以围成一个长方体？二、棱长总和公式：1.长方体棱长总和公式：2.正方体棱长总和公式：【练】1.一个长方体，长、宽、高分别是a、b、c厘米，长、宽、高的和是（）厘米，棱长的和是（）厘米。

2.一个正方体的棱长是a厘米，棱长的和是（）厘米。

如果a=6，那么它的棱长的和是（）厘米。

3.一种长方体的广告灯箱，框架由铝合金条制成，长70厘米，宽15厘米，高120厘米，制作一个这样的广告灯箱，至少需要铝合金条多少分米？4.一个长方体纸箱，长和宽都是0.4米，高是1.2米，做这个纸箱至少需要多少平方米的纸板。

V=
V=
a
3
sh
返回
难度
口答
3dm 4dm 2dm
1、这个牛奶箱的体积是多少 ?
2、不计算接头处与损耗材料，做 一个牛奶箱包装盒最少需要多少硬纸？
3、魔方的表面积和体积各是多少？
6cm
6cm
6cm
返回
难度
完成选择题
返回
1、用一条长60厘米的铁丝围成一个正方 体，这个正方体的棱长是（ ）厘米。
A 60÷10=6厘米 B 60÷4=15厘米 C 60÷12=5厘米
6.下面是长方体和正方体的表面积展开图，你能 先测量，再分别算出它们的表面积和体积吗？ 2cm 1.5cm 1cm 0.9cm
2×1.5×2＋2×1×2＋1.5×1×2 ＝6＋4＋3 0.9×0.9×6 ＝13（cm²） ＝4.86（cm²） 2×1.5×1 0.9×0.9×0.9 ＝3（cm³） ＝0.729（cm³）
● ●
12个底面积：
2.4×0.8×12＝1.92×12＝23.04(平方米 12根立柱的体积： 2.4×0.8×11.5×12 ＝23.04×11.5＝264.96(立方米)
●●
●●
四周：2.4×11.5×2＋0.8×11.5×2 ＝2.4×23＋0.8×23 ＝73.6（平方米） 上面：2.4×0.8＝1.92（平方米） 73.6＋1.92＝75.52（平方米）
11.用小棒和橡皮泥团，可以做出不同的长 方体和正方体框架。小组合作，先填写选 料单，再做一做。
12.调查几种长方体形状家用电器长、宽、 高的数据，算出它们的表面积和体积。
13.你能求出一张纸的体积吗？小组合作， 动手试一试。
4×4×4－（1＋4＋9） ＝64－14 ＝50（个） 7＋12＋15＋16 ＝50（个）

便选择合适的解题方法。
建立模型
对于复杂的问题，可以尝试建 立数学模型，以便更直观地理
解问题并找到解决方案。
多做练习
通过大量的练习，可以加深对 知识点的理解，提高解题的准
确性和效率。
06 复习策略与建议
系统回顾本单元知识点
长方体和正方体的定义与性质
理解长方体和正方体的基本概念，掌握它们的面、棱、 顶点等要素的数量关系和位置关系。
01 03
性质
02
正方体的所有面都是全等的 正方形。
长方体与正方体关系
正方体是长方体的特例，当长 方体的三组对边分别相等时， 即为正方体。
长方体和正方体都有6个面、 12条棱和8个顶点。
长方体和正方体的表面积和体 积计算公式不同，需要根据具 体形状进行区分和应用。
02 长方体和正方体表面积计 算
03 长方体和正方体体积计算
长方体体积公式推导
长方体体积公式为
$V = l times w times h$，其中 $l$ 是长度，$w$ 是宽度，$h$ 是高度。
公式推导
长方体可以看作是由 $l$ 个长度为 $w$， 高度为 $h$ 的小长方体组成，因此总 体积就是 $l times w times h$。
05 易错点与注意事项
常见易错点总结
概念混淆
学生容易混淆长方体和正方体的 概念，特别是在面对复杂图形时。
计算错误
在计算表面积或体积时，学生可能 会因为疏忽或计算不准确而导致错 误。
单位问题
在解决实际问题时，学生可能会忽 略单位换算，从而导致答案错误。
避免错误方法指导
01
02
03
明确概念
在解题前，首先要明确题 目中涉及的是长方体还是 正方体，以及它们的基本 性质。

典型例题解析
例题1
解析
一个长方体的长、宽、高分别为5cm、3cm、 2cm，求它的表面积。
根据长方体表面积公式S = 2(ab + bc + ac)， 将长、宽、高分别代入公式，得到S = 2(5×3 + 3×2 + 5×2) = 98cm^2。
例题2
解析
一个正方体的棱长为4cm，求它的表面积。
根据正方体表面积公式S = 6a^2，将棱长代 入公式，得到S = 6×4^2 = 96cm^2。
长方体和正方体整理 与复习ppt课件
目录
CONTENTS
• 长方体与正方体基本概念 • 长方体和正方体表面积计算 • 长方体和正方体体积计算 • 长方体和正方体在生活中的应用 • 拓展内容：不规则物体体积计算 • 课程总结与回顾
01 长方体与正方体基本概念
长方体定义及性质
长方体定义
长方体是由六个矩形围成的立体 图形，相对的两个面相等且平行 。
学习态度与习惯
我始终保持积极的学习态度和良 好的学习习惯，认真听讲、积极 思考、及时复习，这些都有助于
我取得更好的学习效果。
下一步学习计划建议
深入探究相关知识点
在掌握了长方体和正方体的基本知识点后， 我将进一步探究与之相关的知识点，如圆柱 体、圆锥体等立体图形的性质与计算。
拓展学习领域
除了本课程的知识点外，我还将积极拓展 学习领域，了解更多的数学知识和应用实 例，提高自己的数学素养和综合能力。
问题类型
不规则物体体积计算问题常常出现在各 种实际场景中，如工程测量、物体设计 等。
VS
解决方法
针对不同类型的问题，可以选择合适的间 接方法进行求解。例如，对于难以直接计 算的不规则物体，可以通过构建长方体或 球体等规则物体，利用它们的体积公式进 行间接计算。

总结词
长方体和正方体的边长关系是它们之 间转换的关键，正方体的边长等于长 方体的棱长。
详细描述
正方体是特殊的长方体，其三个边长 都相等。当长方体的三个边长相等时， 它就变成了正方体。反之，如果一个 长方体的三个边长不相等，它就不是 正方体。
表面积与体积的关系
总结词
长方体和正方体的表面积和体积计算公式是 它们之间的重要关系。
实例与应用
实例
一个长方体的长为4cm，宽为3cm， 高为2cm，求其表面积。
Байду номын сангаас应用
在实际生活中，长方体和正方体 的表面积计算可以应用于各种场 景，如制作纸盒、包装设计、建 筑材料等。
常见错误解析
01
02
03
错误1
计算长方体的表面积时忘 记乘以2。
错误2
计算正方体的表面积时忘 记乘以6。
错误3
混淆长方体和正方体的表 面积公式。
分类与区别
总结词
长方体和正方体的分类与区别是理解这两种几何体的关键。
详细描述
根据长宽高的不同，长方体可以分为三类：等宽等高、等宽不等高、等高不等宽。正方体是特殊的长方体，它的 长宽高都相等。长方体和正方体的区别在于它们的面和棱的数量、形状和大小。此外，它们的空间占据性和封闭 性也有所不同。
02
长方体和正方体的表面积计算
实例与应用
总结词
通过实例和应用来巩固长方体和正方体体积计算公式的理解和运用。
详细描述
可以通过生活中的实际例子来解释长方体和正方体体积计算公式的应用，如计算房间的容积、冰箱的 存储容量等。此外，在建筑、工程等领域中，长方体和正方体的体积计算也是非常重要的。
常见错误解析
总结词

《长方体正方体整理与复习》教学设计《长方体正方体整理与复习》教学设计（通用10篇）作为一位优秀的人民教师，时常需要准备好教学设计，借助教学设计可以让教学工作更加有效地进行。

我们应该怎么写教学设计呢？下面是小编收集整理的《长方体正方体整理与复习》教学设计，仅供参考，大家一起来看看吧。

《长方体正方体整理与复习》教学设计篇1教学目标：1、通过整理、复习，使学生进一步掌握长方体和正方体的特征，表面积、体积的概念以及相邻单位间的进率；能进一步认识长方体、正方体的表面积和体积及其计算方法，并能正确地计算。

理解它们的内在联系，能灵活运用。

2、在学生对这些形体认识和理解的基础上，进一步培养空间观念；让学生在解决实际问题的过程中，感受数学在生活中的作用，体会数学的价值，进一步培养学生的合作意识和创新精神。

教学重点、难点：学生对知识进行自我梳理，灵活运用知识解决实际问题教学准备：课件、题卡教学过程设计：一、创设情境导入新课1、同学们，这节课我们一起来整理复习长方体、正方体的相关知识。

（板书课题）2、我们一起回顾一下，通常我们是怎样整理复习学过的知识？学生回答：整理出所学知识的主要内容、梳理出知识之间的联系、灵活运用知识解决实际问题。

随机板书：知识点、联系、实际应用3、这节课我们就应用这种方法来整理这两种立体图形的相关知识。

二、自我梳理形成网络1、小组合作整理课前大家已经对这部分知识进行了整理，现在拿出你们的数学整理记录单，把你整理的内容先在小组内交流，并解决你在复习中的问题。

如果发现在整理中有遗漏的内容，就边交流边补充到整理记录单中。

一会在全班进行交流。

看哪个小组对这部分知识梳理得更完整、更全面。

在学生交流的过程中，教师巡视，把整理的有特色的教师要做到心中有数，便于稍后的交流[设计意图：这个环节体现了学生能有条理的独立整理复习所学知识具有良好的整理复习的能力和习惯，在小组交流中能主动与他人合作，遇到困难能主动请教他人，善于在学习中总结与反思，从而取长补短提高学习的效率和能力。

课题长方体和正方体教学目标1、认识长方体和正方体2、长方体和正方体的表面积3、长方体和正方体的体积重点、难点掌握长方体和正方体的表面积和体积的计算考点及考试要求1、长方体和正方体的表面积和体积的计算2、组合立体图形的表面积和体积的计算教学内容知识框架长方体和正方体的知识是学生进行表面积和体积计算的基础知识，是运用有关的计算公式可解决许多实际问题。

考点一：认识长方体和正方体典型例题例一：判断对错。

（1）棱长 5分米的正方体水箱，它的占地面积是（125）平方分米。

（）（2）长方体（不含正方体）最多有8条棱长度相等。

（）（3）正方体是特殊的立方体。

（）（4）有6个面，12条棱，8个顶点组成的图形都是长方体。

（）（5）相交于一个顶点的三条棱的长度相等的长方体一定是正方体。

（）（6）两个体积相等的立方体，表面积也一定相等。

（）例二：有30个棱长为1厘米的小正方体（1）怎样摆才能将它拼成一个最大的正方体？还剩几个小正方体？例三：一个正方体木块，六个面上分别写着1、 2 、 3 、 4 、 5 、6，从三个不同角度观察结果如下，请你猜一猜：1、2、3分别和谁相对？知识概括、方法总结与易错点分析长方体和正方体都有六个面，正方体六个面都相等；长方体对面相等，最多可有两个正方形。

考点二：长方体和正方体的表面积典型例题例一：1. 长方体和正方体都有（）面，（）条棱和（）顶点。

2.（1）一个长方体的长、宽、高分别是5、4、3厘米，这个长方体的棱长总和是（）。

（2）一个长方体相交一个顶点的三条棱的和是6厘米，这个长方体的棱长总和是（）。

（3）一个正方体的棱长是3分米，这个正方体的棱长总和是（）。

3. 一个正方体的棱长总和是96厘米，这个正方体的棱长是（）。

4. 一个长方体的棱长总和是24厘米，其中长是3厘米，宽是2厘米，高是长（）。

5. 一个长方体的长、宽、高分别是6厘米、5厘米、4厘米，它的最大面的面积是（）。

这个长方体的占地面积是（）。

(1)(30×20+30×15+20×15)×2=2700(平方厘米)
(2)(30÷5)×(20÷2)×(15÷3)=300(块)
4.一个长方体底面是一个边长为20厘米的正方 形，高为40厘米，如果把它的高增加5厘米，它 的表面积会增加多少？
6.至少要（8 ）个小正方体才能拼成一个大正方体，小正方体的 棱长是2cm，那么大正方体的表面积（96c）m，2 体积是（64c）m3
7.一根长20分米的长方体钢材，沿横截面截成两段后，表面积 增加0.8dm2,这段钢材的体积是（8dm）3。
8.一个长10厘米，宽8厘米，高12厘米的长方体木块放在桌面上， 占桌面的面积最大是（ ）平方厘米。
长方体和正方体 整理与复习
知识树
意义 计算
表面积
棱 面
顶点
特征
意义 单位、进率 计算
长
体积
方
体
和
正
方
体
长方体和正方体的特征
相同点
不同点
联系
形体
面 棱 顶点
面的 形状
面的 面积
棱长
长方体
6 12 个条
正方体
6个面都是长 相对的 方形，有时相 两个面
相对的棱
的长度相 等
正方体
对的两个面是 的面积 棱长和 是一种
2.用一段铁丝，正好可以做一个长7厘米、宽6 厘米、高5厘米的长方体框架。如果用这段铁丝 做一个正方体的框一根长52厘米的铁丝，恰好可以焊接成 一个长6厘米，宽4厘米，高多少厘米的长方 体？
4、用96厘米长的铁丝焊接成一个正方体的框 架，然后用纸给它的表面包裹起来，至少需 要多少平方厘米的纸？
＝71.4＋50.4 ＝121.8（米²） 粉刷面积＝51＋121.8―35.8＝137（米²）

正方体
正方体是特殊的长方体，每个面都是一个正方形，所有面的面积相等，并且所 有棱的长度都相等。
长方体和正方体的性质
长方体的对角线
正方体的对角线
长方体的对角线是连接两个相对顶点的线 段，其长度等于长、宽、高的平方和的平 方根。
长方体的内角
正方体的对角线是连接两个相对顶点的线 段，其长度等于正方体棱长的2倍。
长方体正方体单元整理和复习
2023-11-10
目录
• 长方体正方体的基本概念 • 长方体正方体的空间关系 • 长方体正方体的体积和面积 • 长方体正方体的应用 • 长方体正方体的复习题
01 长方体正方体的基本概念
长方体和正方体的定义
长方体
长方体是一种具有六个面的三维图形，由六个长方形构成，相对的两个面平行 且相等。
空间中的距离
点到直线的距离
在空间中，一个点到一条直线的距离可以通过投影或使用向量运算来计算。
点到平面的距离
在空间中，一个点到平面的距离可以通过点到平面的垂线段来计算。
03 长方体正方体的体积和面 积
体积的定义和计算方法
体积的定义
体积是指物体所占空间的大小。对于长 方体和正方体，我们可以将其看作是具 有一定长、宽、高的立方体。
作为基础几何形状，可以用于研究 数学问题
05 长方体正方体的复习题
基础题
总结长方体和正方体 的基本性质和特点。
理解长方体和正方体 的空间关系和相对位 置。
掌握长方体和正方体 的表面积和体积的计 算方法。
提高题
灵活运用长方体和正方体的性 质和特点解决实际问题。
掌握长方体和正方体的拼接、 分割、旋转等变换方法。
VS
体积的计算方法
长方体的体积可以通过长、宽、高的乘积 来计算，即体积 V = 长 × 宽 × 高。对于 正方体，由于其长、宽、高相等，所以体 积 V = 边长 × 边长 × 边长。

第三单元长方体和正方体整理与复习一、选择题1．用一根72厘米长的铁丝正好弯成一个长方体框架，那么这个长方体一组长、宽、高的和是（）厘米。

A．36B．24C．182．一个矿泉水瓶的容积大约为350（）。

A．毫升B．升C．立方分米D．立方米3．用棱长2厘米的正方体木块拼成一个较大的正方体，至少需要（）块。

A．4B．8C．9D．644．一个长方体水池，长20米，宽10米，深2米，占地（）平方米。

A．200B．400C．5205．下面的平面图中，（）个字母代表的平面图不能折成正方体。

A．B．C．D．6．一根长40分米的铁丝焊成一个长方体框架，还余4分米，这个长方体框架中相交于一点的三条棱的长度和是（）分米。

A．12B．9C．67．观察这是（）个小正方体，两面靠墙，露出（）个平面。

A．3、3B．2、3C．1、38．求做一个长方体油箱需要多少平方米铁皮，是求长方体的（）。

A．表面积B．体积C．容积D．不能确定9．如果一个长方体有四个面的面积相等，剩下的两个面一定是（）。

A．长方形B．正方形C．平行四边形10．如果把长方体的长、宽、高都分别扩大到原来的2倍，那么它的体积就扩大到原来的（）倍。

A．2B．4C．6D．811．如图是一个正方体的展开图，和2号面相对的面是（）。

A．3号B．4号C．6号12．一个长6dm、宽4dm、高5dm的盒子，最多能放（）个棱长为2dm的正方体木块。

A．10B．12C．14D．15二、填空题13．一个长方体长3m、宽1.5m、高2m，这个长方体的棱长之和是________m，表面积是________m2，体积是________m3。

14．两块同样大小的陶土，一块做了棱长是15厘米的正方体，另一块做了底面积是300平方厘米的长方体。

这个长方体的高是________厘米。

15．如图，两个正方体拼成一个长方体后，表面积减少12cm2。

现在这个长方体的表面积是________cm2。

16．一个正方体纸盒的棱长总和是60分米，它的占地面积是( )，表面积是( )，体积是( )。