蔡氏混沌电路简介——Chua's Circut

非线性电路混沌实验混沌是非线性系统中存在的一种普遍现象，它也是非线性系统所特有的一种复杂状态。

混沌研究最先起源于 1963年洛伦兹（E.Lorenz ）研究天气预报时用到的三个动力学方程 ,后来又从数学和实验上得到证实。

无论是复杂系统，如气象系统、太阳系，还是简单系统，如钟摆、滴水龙头等，皆因存在着内在随机性而出现类似无轨、 但实际是非周期有序运动，即混沌 现象。

由于电学量（如电压、电流）易于观察和显示，因此非线性电路逐渐成为混沌及混沌同 步应用的重要途径，其中最典型的电路是美国加州大学伯克利分校的蔡少棠教授 1985年提 出的著名的蔡氏电路（Chua ' s Circuit ）。

就实验而言，可用示波器观察到电路混沌产生的全 过程,并能得到双涡卷混沌吸引子。

本实验所建立的非线性电路包括有源非线性负阻、 LC 振荡器和RC 移相器三部分；采用 物理实验方法研究 LC 振荡器产生的正弦波与经过 RC 移相器移相的正弦波合成的相图（李萨如图），观测振动周期发生的分岔及混沌现象。

【实验目的】观测振动周期发生的分岔及混沌现象； 测量非线性单元电路的电流一电压特性；了解非线性电路混沌现象的本质； 学会自己制作和测量一个使用带铁磁材料介质的电感器以及测量非线性器件伏安特性的方法。

【实验原理】1. 非线性电路与非线性动力学实验电路如图1所示，图1中只有一个非线性元件 R ，它是一个有源非线性负阻器件。

电感器L 和电容C 2组成一个损耗可以忽略的谐振回路； 可变电阻R V 和电容器C 串联将振荡器产生的正弦信号移相输出。

本实验中所用的非线性元件 R 是一个三段分段线性元件。

图2所示的是该电阻的伏安特性曲线， 从特性曲线显示中加在此非线性元件上电压与通过它的电流极性是相反的。

由于加在此元件上的电压增加时，通过它的电流却减小， 因而将此元件称为非线性负阻元件。

图1电路的非线性动力学方程为:C 2dU C L二 G (U C 1 -U C 21)I L(1)dt121C 1du e ’ dt=G (U C 2 -Uq) _g UqLd L实际非线性混沌实验电路如图式中，导纳G =1/R/ , U c.和U c2分别为表示加在电容器C和C2上的电压，i L表示流过电感器L的电流，G表示非线性电阻的导纳。

四阶蔡氏电路的建模与仿真摘要：混沌现象是一种确定性的非线性运动，在非线性控制领域，混沌控制的研究受到人们越来越多的关注。

典型蔡氏电路结构简单，但有复杂的混沌动力学特征，因而在混沌控制领域中成为研究的重要对象。

本次设计简单介绍了混沌学基本理论，从理论分析和仿真实验两个角度分别研究Chua's Circuit 的混沌行为，用Multisim 软件对电路进行仿真实验，通过改变参数，得到了系统各周期的相轨图，并对实验中遇到的现象进行简单的讨论。

在三阶蔡氏电路的基础上添加一个电感，可以建立四阶蔡氏电路，在此四阶蔡氏电路的基础上，进行了简单的数值分析与仿真分析。

由于普通蔡氏电路在产生混沌现象时, 其元件参数可调围很小,且对初始条件极为敏感，不易于搭建实验电路。

所以引入了电感等效电路，在本文中将蔡氏电路中的电感用等效电路替代，从而实现了无感蔡氏电路。

关键词：混沌；蔡氏电路；Multisim ；等效电感Experimental Study of Chua's circuit chaoticAbstract ：Chaos is a deterministic non-linear movement, in the field of nonlinear control, chaotic control get more and more attention by people. Typical Chua's circuit is simple, but complex and chaotic dynamics characteristics, so become an important research object in the field of chaos control . The design simple introduced the basic theory of chaos, study the chaotic behavior of Chua'sCircuit from two angles of the theoretical analysis and experimental with Multisim circuit simulation software, by changing the parameters, get each cycle tracks phase diagram of the system, simple discuss the experimental phenomena encountered, couple the second-order Chua's circuit with a linear circuit ("oscillation absorber"), get even more chaotic behavior of the rich. As the general chaos in Chua's circuit in the production, its range of component parameters adjustable is very small, and extremely sensitive to initial conditions, hard to set up experimental circuit. Therefore introduce the inductor equivalent circuit, in this final, change the inductor of Chua's circuit with the equivalent circuit, thus achieving non- inductor of Chua's circuit.Key words ：chaos; Chua's circuit; Multisim; vibration absorber; equivalent inductance目录第一章混沌学基本理论. (5)1.1 混沌的简单介绍 (5)1.1.1 混沌的定义. (5)1.1.2 混沌的主要特征. (6)1.1.3 混沌的现实意义和应用. (7)1.1.4 混沌的前景展望. (8)1.2 蔡氏电路简介 (9)1.3 蔡氏电路的研究 (10)1.4 软件介绍 (10)1.4.1 数值仿真软件. (10)1.4.2 电路仿真软件. (11)第二章三阶蔡氏电路分析. (12)2.1 电路原理与数学建模 (12)2.2 数值仿真分析 (13)2.3 蔡氏二极管等效电路设计 (15)2.4 三阶蔡氏电路制作和电路仿真 (17)2.5 蔡氏电路的平衡点及稳定性 (19)第三章四阶蔡氏电路分析. (22)3.1 四阶蔡氏电路数学建模 (22)3.2 四阶蔡氏电路数值仿真分析 (24)3.3 四阶蔡氏电路电路仿真分析. (25)3.4 三阶蔡氏电路等效电感分析 (27)第四章总结与分析. (30)参考文献. (31)致. (32)附录Matlab 程序 (33)第一章混沌学基本理论1.1 混沌的简单介绍1.1.1 混沌的定义混沌是非线性动力学系统所特有的一种运动形式，是自然界及社会中的一种普遍现象，它是一种在确定性系统中所出现的类似随机而无规则运动的动力学行为。

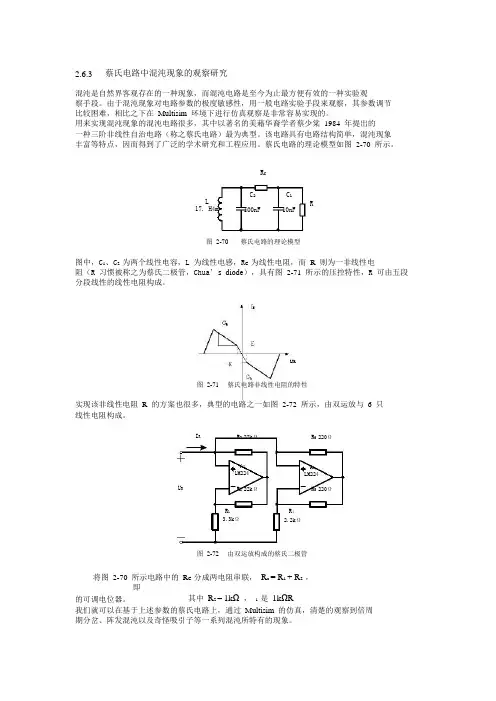
2.6.3蔡氏电路中混沌现象的观察研究混沌是自然界客观存在的一种现象，而混沌电路是至今为止最方便有效的一种实验观察手段。

由于混沌现象对电路参数的极度敏感性，用一般电路实验手段来观察，其参数调节比较困难，相比之下在Multisim 环境下进行仿真观察是非常容易实现的。

用来实现混沌现象的混沌电路很多，其中以著名的美藉华裔学者蔡少棠1984 年提出的一种三阶非线性自治电路（称之蔡氏电路）最为典型。

该电路具有电路结构简单，混沌现象丰富等特点，因而得到了广泛的学术研究和工程应用。

蔡氏电路的理论模型如图2-70 所示。

R CLC2100nFC1 10nF17. H4mR图2-70蔡氏电路的理论模型图中，C1、C2 为两个线性电容，L 为线性电感，R C 为线性电阻，而R 则为一非线性电阻（R 习惯被称之为蔡氏二极管，Chua’s diode），具有图2-71 所示的压控特性，R 可由五段分段线性的线性电阻构成。

U R图2-71蔡氏电路非线性电阻的特性实现该非线性电阻R 的方案也很多，典型的电路之一如图2-72 所示，由双运放与 6 只线性电阻构成。

I R R3 22kΩR6 220ΩA1 LM224A1 LM224U RR1R2 22kΩR42.2kΩR5 220Ω3.3kΩ图2-72由双运放构成的蔡氏二极管将图2-70 所示电路中的R C 分成两电阻串联，R c = R1 + R2 ，即其中R2 = 1kΩ， 1 是1kΩR的可调电位器。

我们就可以在基于上述参数的蔡氏电路上，通过Multisim 的仿真，清楚的观察到倍周期分岔、阵发混沌以及奇怪吸引子等一系列混沌所特有的现象。

1．编辑原理图首先编辑非线性电阻R 构成电路，如图2-73 (a)所示。

在这个图中取用两个输入接线端，是为了把该电路设置成如图2-73 (b)所示的R 子电路。

(a)图2-73(b) Multisim 中编辑出的非线性电阻R 及其子电路子电路的创建方法是在选中图中所有的部分（按住鼠标，拖一个把该电路部分全部包围进去的方框，如电路窗口中仅有这部分电路，也可选择Edit/Select All 命令），启动Place/Replace by Subcricuit 命令，即可得。

蔡氏对偶混沌电路分析与仿真硕0027班吴旋律 3110163015 一、引言混沌是非线性动力学系统所特有的一种运动形式，它是一种在确定型系统中所出现的类似随机而无规则的动力学行为。

由于其对初始值的极端敏感性和类噪声性，在保密通信技术和扩频通信技术中具有广阔的应用前景。

1983年，美国贝克莱（Berkeley）大学的蔡少堂教授（Leon.o.Chua）发明了蔡氏电路（Chua’s Circuit），蔡氏电路因其简洁性和代表性而成为研究非线性电路中混沌的典范。

本文讨论一个新颖的蔡氏对偶混沌电路，对其进行理论分析并且给出计算机仿真方法以及仿真结果。

二、蔡氏对偶混沌电路分析本文讨论的电路与著名的蔡氏电路形成完全对偶的电路结构，是一个三阶自治电路，其中含有一个流控型非线性电阻元件。

电路图和非线性电阻伏安特性如下图所示。

u r=r(i1)根据上图可以得到电路的状态方程组：L1di1dt=R0(i2−i1)−r(i1) (1)L2di2dt=R0(i1−i2)+u c (2)C du cdt=−i2 (3) 从以上三个方程可以得出：di1 dt =R0L1(i2−i1)−1L1r(i1) (4)di2 dt =R0L2(i1−i2)+1L2u c (5)du c dt =−1Ci2 (6)为了分析方便，我们对方称进行归一化处理。

令t=L2R0τ ,dτ=R0L2dtx=i1,y=i2,z=u c R0则上述方程变为：dx dτ=L2L1,y−x−r(x)-dydτ=x−y+zdzdτ=−L2CR02yy将上述方程中的τ仍然记做t，则上述方程就变换为（7）-（9）标准的蔡氏方程。

dxdt=α,y−f(x)- (7)dydt=x−y+z (8)dzdt=−βy (9) 其中α=L2L1,β=L2CR02,r(x)=f(x)=m1x+0.5(m0−m1)(|x+1|−|x−1|)可以看出，（7）-（9）式与描述蔡氏电路的动态方程完全一致。

蔡氏混沌非线性电路的研究摘要本文首先介绍非线性系统中的混沌现象，并从理论分析与仿真计算两个方面细致研究了非线性电路中典型混沌电路，即蔡氏电路反映出的非线性性质。

通过改变蔡氏电路中元件的参数，进而产生多种类型混沌现象。

最后利用软件对蔡氏电路的非线性微分方程组进行编程仿真，实现了双涡旋和单涡旋状态下的同步，并准确地观察到混沌吸引子的行为特征。

关键词：混沌；蔡氏电路；MATLAB仿真AbstractThis paper introduces the chaos phenomenon in nonlinear circuits. Chua’s circuit was a typical chaos circuit, thus theoretical analysis and simulation was made to research it. Many kinds of chaos phenomenon on would generate as long as one component parameter was altered in Chua’s circuit．On the platform of Matlab, mathematical model of Chua’s circuit was programmed and simulated to acquire the synchronization of dual and single cochlear volume. Meanwhile, behavioral characteristics of chaos attractor were observed.Key words：chaos phenomenon；Chua’s circuit；simulation一．引言：混沌是一种自然界普遍存在的非线性现象，随着计算机的快速发展，混沌现象及其应用已成为自然科学和社会科学领域的一个重点研究对象。

非线性电路混沌效应——湖南工程学院理学院 物理实验中心混沌理论（Chaos theory）是关于非线性系统在一定参数条件下展现分岔（bifurcation）、周期运动与非周期运动相互纠缠，以至于通向某种非周期有序运动的理论。

在耗散系统和保守系统中，混沌运动有不同表现，前者有吸引子，后者无（也称含混吸引子）。

从20世纪80年代中期到20世纪末，混沌理论迅速吸引了数学、物理、工程、生态学、经济学、气象学、情报学等诸多领域学者有关注，引发了全球混沌热。

混沌，也写作浑沌（比如《庄子》）。

自然科学中讲的混沌运动指确定性系统中展示的一种类似随机的行为或性态。

确定性（deterministic）是指方程不含随机项的系统，也称动力系统（dynamical system）。

典型的模型有单峰映象（logistic map）迭代系统，洛伦兹微分方程系统，若斯叻吸引子，杜芬方程，蔡氏电路，陈氏吸引子等。

为浑沌理论做出重要贡献的学者有庞加莱、洛伦兹、上田睆亮（Y. Ueda）、费根堡姆、约克、李天岩、斯美尔、芒德勃罗和郝柏林等。

混沌理论向前可追溯到19世纪庞加莱等人对天体力学的研究，他提出了同宿轨道、异宿轨道的概念，他也被称为浑沌学之父。

近半世纪以来，科学家发现许多自然现象即使可以化为单纯的数学公式，但是其行径却无法加以预测。

如气象学家爱德华·诺顿·劳仑次（Edward Lorenz）发现简单的热对流现象居然能引起令人无法想象的气象变化，产生所谓的“蝴蝶效应”。

60年代，美国数学家史蒂芬·斯梅尔（Stephen Smale）发现某些物体的行径经过某种规则性变化之后，随后的发展并无一定的轨迹可循，呈现失序的混沌状态。

在电路系统中最著名的非线性电路是蔡氏电路。

【基本理论】一、线性与非线性理论。

线性（linear）：指量与量之间按比例、成直线的关系，两个变量之间存在一次方函数关系。

非线性（non-linear）：则指不按比例、不成直线的关系，即 变量之间的数学关系，不是直线而是曲线、曲面、或不确定的属性。

文章编号:1008-0686(2002)05-0005-03蔡氏混沌非线性电路及其频率特性研究蒋国平,程艳云(南京邮电学院电子工程系,江苏南京　210003)α摘　要:混沌电路是一种非线性电路,具有宽频谱特性,但在实际通信应用中,通信信道的带宽有一定限制,如何调节混沌电路的频谱范围成为混沌电路实际应用的一个问题。

本文以蔡氏混沌电路为例,利用M A TLAB软件分析蔡氏混沌电路产生的混沌信号及其频率特性。

通过对蔡氏混沌电路中元器件R、L和C参数的调整,可以获得具有期望频谱范围的混沌信号。

关键词:混沌;蔡氏电路;频率特性Study on Chuaπs Non l i near Chaotic C ircu it and Its Frequency Character isticJ i ang Guo-p i ng,CHENG Yan-yun(E lectronic E ng ineering D ep art m ent,nanj ing U niversity of P osts&T eleco mm unications,N anj ing210003,Ch ina)Abstract:Chao tic signal has the characteristic of large frequency band2w idth.How ever,in the real comm u2 n icati on app licati on,there is a li m itati on to the band2w idth fo r the channel.T hu s,how to adju st the fre2 quency bandw idth fo r real app licati on is a p rob lem in con siderati on.In th is p ap er,w e analyze the frequen2 cy sp ectrum in Chuaπs circu it w ith M atlab softw are.W e can ob tain the chao tic signal w ith the desired fre2 quency band2w idth by adju sting the p aram eters of Chuaπs circu it.Keywords:chao s;Chuaπs circu it;frequency characteristic0　引言混沌电路与系统理论经过30多年的发展,在科学和工程中得到了广泛的应用。

蔡氏混沌电路分析研究蔡氏混沌电路分析研究摘要：众所周知，蔡氏电路是一种简单的非电子性电路设计，它可以表现出标准的混沌理论行为。

混沌是一种发生在确定系统中的不确定行为，表现为不同于平衡状态、周期状态和拟周期状态的这三种状态外的另一种状态，产生的混沌现象极为丰富。

随着社会的开展，混沌动力学以其内容丰富的特点，成为了一个被广泛研究应用的知识学科。

混沌现象是产生于确定性的状态方程中的一种相似随机的运动，在我们现实生活中较为广泛的存在。

在工程和电工电子学科上最近几年的开展前景也越来越开阔和活泼。

随着时代开展，在现实生活中，混沌应用取得了很大的成果，得到了广泛的成果研究。

尤其是混沌独电路这一局部，其中包括混沌压缩、混沌保密通信、混沌加密和混沌同步。

但是还有一些实际问题需要探讨和研究，作者通过文章来介绍蔡氏混沌电路的电路设计根底与存在的问题及其面临的挑战与机遇。

关键词：混沌电路；广泛；开展；问题文章着重介绍了蔡氏混沌电路的根本设计思路与混沌系统分析方法和混沌电路的根底设计，依据国内外对电路的研究，分析当前各种混沌系统，总结得出混沌电路的开展历史。

文章在理论根底的分析和参考文献研的前提下，对混沌电路的动力学行为的复杂性提出了一种具有多方向多漩涡吸引子的可扩展的蔡氏电路；对混沌振荡的频率那么提出了如MOS管的Colpitts振荡电路设计和同步的一种方法。

20年的时间，人们对蔡氏混沌电路的深入研究与探究，我们发现在蔡氏电路里呈现出来一种丰富的混沌力学行为。

且蔡氏混沌电路已经在保密通讯领域具备了一定的应用能力。

混沌学，是继量子论、相对论的20世纪第三次物理革命产物。

法国数学家在19世纪末期首次发现了动力学系统中的异归宿轨迹和同归宿轨迹，混沌现象作为存在在非线性动力学系统中的一种现象，虽没有复杂的运动形式，但具有普遍性的规律。

1 蔡氏混沌电路工作原理的介绍与研究意义蔡氏混沌电路由线性电感、线性电阻、非线性电阻各一个和线性电容两个组成的三阶段自治动态电路，非线性电阻的伏特安特性，是一个分段型函数，电路中电感L和电容LC振荡电路，有原型的电阻R和电容做成了一个源RC滤波电路。