指、对数函数与反函数

指数函数与对数函数的运算指数函数与对数函数的运算是高等数学中一种重要的数学运算方法。

指数函数是一种以底数为常数，指数为变量的函数，表示为f(x) = a^x，其中a为底数。

对数函数是指数函数的逆运算，表示为f(x) = log_a(x)，其中a为底数。

指数函数与对数函数之间存在一种特殊的运算关系，即指数函数和对数函数是互为反函数的。

这意味着，对于任意的底数a和指数x，有a^log_a(x) = x，以及log_a(a^x) = x。

这一性质使得指数函数和对数函数可以进行运算，并且能够相互抵消。

一、指数函数的运算性质指数函数的运算包括指数相加、指数相减、指数相乘以及指数的幂运算等。

下面将一一介绍这些运算性质。

1. 指数相加：对于相同底数a，两个指数相加的结果等于将底数相乘，指数相加的结果为b^x1*b^x2 = b^(x1+x2)。

例如，2^3 * 2^4 =2^(3+4) = 2^7。

2. 指数相减：对于相同底数a，两个指数相减的结果等于将底数相除，指数相减的结果为b^x1/b^x2 = b^(x1-x2)。

例如，5^8 / 5^3 = 5^(8-3) = 5^5。

3. 指数相乘：对于相同底数a，两个指数相乘等于底数为b，指数为(x1*x2)的指数函数，即(b^x1)^x2 = b^(x1*x2)。

例如，(6^3)^2 =6^(3*2) = 6^6。

4. 指数的幂运算：指数的幂运算即多次将相同的底数相乘，指数的幂运算的结果为(b^x)^n = b^(x*n)。

例如，(3^2)^4 = 3^(2*4) = 3^8。

二、对数函数的运算性质对数函数的运算包括对数相加、对数相减、对数相乘以及对数的幂运算等。

下面将一一介绍这些运算性质。

1. 对数相加：对于相同底数a，两个对数相加的结果等于将指数相加，对数相加的结果为log_a(x1) + log_a(x2) = log_a(x1*x2)。

例如，log_2(4) + log_2(8) = log_2(4*8) = log_2(32)。

指数函数对数函数大小比较的技巧介绍指数函数和对数函数是数学中常见的函数类型，它们在各种科学和工程应用中起着重要的作用。

本文将介绍一些比较指数函数和对数函数大小的技巧，帮助读者更好地理解和应用这两种函数。

指数函数的性质指数函数的一般形式为 y = a^x，其中 a>0 且a≠1。

指数函数的性质如下：1. 当 a>1 时，函数呈现递增趋势，即 x 增大时，y 也增大。

2. 当 0<a<1 时，函数呈现递减趋势，即 x 增大时，y 减小。

3. 当 x=0 时，指数函数的值为 1，无论 a 的取值如何。

对数函数的性质对数函数的一般形式为y = logₐx，其中 a>0 且a≠1。

对数函数的性质如下：1. 对数函数是指数函数的反函数，即a^logₐx = x。

2. 当 0<x<1 时，对数函数的值为负数。

3. 当 x=1 时，对数函数的值为 0。

4. 当 x>1 时，函数呈现递增趋势，即 x 增大时，y 也增大。

5. 当 0<x<1 时，函数呈现递减趋势，即 x 增大时，y 减小。

6. 当 x=0 时，对数函数的值为负无穷大，即logₐ0 = -∞。

比较指数函数和对数函数大小的技巧1. 当 a>1 时，指数函数的值始终大于对数函数的值。

2. 当 0<a<1 时，指数函数的值始终小于对数函数的值。

3. 当 a=1 时，指数函数和对数函数的值相等。

4. 当 x 相同时，指数函数的值通常大于对数函数的值，但有特殊情况，例如 x=0 时，指数函数和对数函数的值相等，都为 1 或 0。

总结通过比较指数函数和对数函数的性质，我们可以得出一些比较大小的技巧。

在应用中，我们可以利用这些技巧更好地理解和使用指数函数和对数函数，从而更好地解决相关问题。

以上是关于指数函数对数函数大小比较的技巧的介绍。

希望本文能对读者有所帮助，谢谢阅读！。

六种基本初等函数（elementary function）
一、常数函数（constant function）
因为f映射任意的值到4，因此函数f(x)是一个常数。

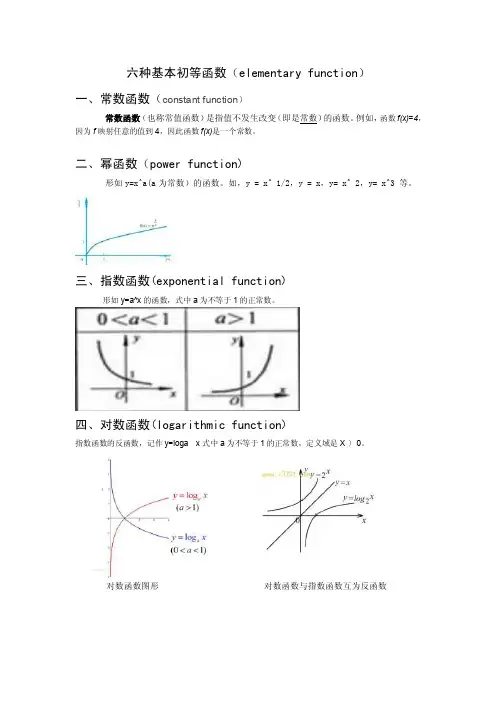
二、幂函数（power function)
形如y=x^a(a为常数）的函数。

如，y = x^ 1/2，y = x，y= x^ 2，y= x^3 等。

三、指数函数(exponential function)
形如y=a^x的函数，式中a为不等于1的正常数。

四、对数函数(logarithmic function)
指数函数的反函数，记作y=loga x式中a为不等于1的正常数，定义域是X〉0。

对数函数图形对数函数与指数函数互为反函数
五、三角函数(trigonometric function)
即正弦函数y=sinx ，余弦函数y=cosx ，正切函数y=tanx，余切函数y=cotx ，正割函数y=secx，余割函数y=cscx。

六、反三角函数(inverse trigonometic function)
反正弦函数y = arcsin x，为y=sin x的反函数反余弦函数y = arccos x，为y=cos x 的反函数
反正切函数y = arctan x，为y=tan x 的反函数反余切函数y = arccot x ，为y=cot x的反函数
反正割函数y = arcsec x ，为y=sec x的反函数反余割函数y = arccsc x ，为y=csc x的反函数七、定义域，值域和单调性。

指数函数、对数函数、幂函数的图像与性质（一）指数与指数函数1．根式（1）根式的概念（2）．两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ；②a a n n =)(（注意a 必须使n a 有意义）。

2．有理数指数幂 （1）幂的有关概念 ①正数的正分数指数幂:0,,1)m na a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)mnm naa m n N n a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注：分数指数幂与根式可以互化，通常利用分数指数幂进行根式的运算。

（2）有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 3．指数函数的图象与性质n 为奇数 n 为偶数注：如图所示，是指数函数（1）y=a x ,（2）y=b x,（3）,y=c x （4）,y=d x 的图象，如何确定底数a,b,c,d 与1之间的大小关系？提示：在图中作直线x=1，与它们图象交点的纵坐标即为它们各自底数的值，即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。

即无论在轴的左侧还是右侧，底数按逆时针方向变大。

（二）对数与对数函数 1、对数的概念 （1）对数的定义如果(01)x a N a a =>≠且，那么数x 叫做以a 为底，N 的对数，记作log N a x =，其中a 叫做对数的底数，N 叫做真数。

（2）几种常见对数2、对数的性质与运算法则（1）对数的性质（0,1a a >≠且）：①1log 0a =，②lo g 1aa =，③lo g Na a N =，④lo g N a aN =。

对数函数的概念与性质对数函数是数学中一种重要的函数类型，它在各个领域的应用中起到了至关重要的作用。

本文将对对数函数的概念及其性质进行探讨，并分析其在数学和实际问题中的应用。

一、对数函数的概念对数函数是指满足特定条件的指数方程的反函数。

具体来说，对于给定的底数a（a > 0, a ≠ 1），任意正实数x，对数函数y=logₐx的定义为y是满足a的y次方等于x的实数，即aᵧ=x。

对数函数的基本特征是“对数”的性质，即对数函数将乘法运算转化为加法运算。

对于任意的正实数x和y，对数函数具有以下性质：1. 对数函数的定义域为正实数集，值域为实数集；2. 对数函数的图象总是经过第一象限和y轴正半轴；3. 对数函数在底数大于1时单调递增，在0 < a < 1时单调递减；4. 对数函数的零点为底数a等于1时的情况，即x=1。

二、对数函数的性质除了上述基本性质外，对数函数还具有以下重要的性质：1. 对数的运算律：- 对于任意正实数x和y，有logₐ(xy) = logₐx + logₐy；- 对于任意正实数x和y，有logₐ(x/y) = logₐx - logₐy；- 对于任意正实数x和任意正有理数r，有logₐxⁿ = n * logₐx；- 特别地，当底数为10时，称为常用对数，表示为logx。

2. 对数函数与指数函数的反函数关系：- 对数函数y=logₐx与指数函数y=aˣ互为反函数；- 对数函数的图象为指数函数的反函数图象关于y=x的对称图象。

三、对数函数的应用对数函数的应用广泛，涵盖了多个领域。

下面简要介绍几个典型的应用：1. 密度和半衰期计算：在物理学和化学中，对数函数经常用于计算物质的密度和半衰期。

对数函数可以将复杂的指数变化转换为更直观的线性变化。

2. 统计学中的财富分布和人口分布：对数函数可以很好地描述财富分布和人口分布等呈现出长尾分布的现象。

通过对数函数的运用，可以更清晰地观察和分析财富和人口的分布规律。

反比例函数1、反比例函数图象：反比例函数的图像属于以原点为对称中心的中心对称的双曲线反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（K≠0）。

2、性质：1.当k>0时，图象分别位于第一、三象限，同一个象限内，y随x的增大而减小；当k<0时，图象分别位于二、四象限，同一个象限内,y随x的增大而增大。

2.k>0时，函数在x<0上同为减函数、在x>0上同为减函数；k<0时，函数在x<0上为增函数、在x>0上同为增函数。

定义域为x≠0；值域为y≠0。

3.因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与x轴相交，也不可能与y轴相交。

4. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2则S1＝S2=|K|5. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴y=x y=-x（即第一三，二四象限角平分线），对称中心是坐标原点。

6.若设正比例函数y=mx与反比例函数y=n/x交于A、B两点（m、n同号），那么A B两点关于原点对称。

7.设在平面内有反比例函数y=k/x和一次函数y=mx+n，要使它们有公共交点，则n^2+4k·m≥（不小于）0。

8.反比例函数y=k/x的渐近线：x轴与y轴。

9.反比例函数关于正比例函数y=x,y=-x轴对称,并且关于原点中心对称.10.反比例上一点m向x、y分别做垂线，交于q、w，则矩形mwqo（o为原点）的面积为|k|11.k值相等的反比例函数重合，k值不相等的反比例函数永不相交。

12.|k|越大，反比例函数的图象离坐标轴的距离越远。

13.反比例函数图象是中心对称图形，对称中心是原点指数函数概念：一般地，函数y=a^x（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R。

log函数的知识点和公式log函数，也叫对数函数，是解决指数运算中的问题的数学工具之一、在数学领域中，对数函数是指以一些正数为底的指数函数的反函数。

即，对于给定的正数a和正数x，我们可以通过求解方程a^y = x来定义对数函数。

1.对数函数的定义：设a是一个大于零且不等于1的正数，x是一个大于零的正数。

则可以定义a为底，x的对数为满足a^y = x的y值。

我们用符号log_a(x)表示y，即log_a(x) = y。

2.常见的对数函数：在数学中，常见的对数函数包括自然对数（以e为底的对数）和常用对数（以10为底的对数）。

- 常用对数：以10为底的对数，记作log(x)。

在常用对数中，对数的底数10通常省略不写，即log(x) = log_10(x)。

3.对数函数的性质：对数函数具有许多重要的性质，如下所示：-对于任意正数a和b，以及任意正整数n，有以下性质：- log_a(1) = 0- log_a(a) = 1- log_a(a^n) = n- log_a(b^n) = n * log_a(b)- log_a(1/b) = - log_a(b)- log_a(x * y) = log_a(x) + log_a(y)- log_a(x / y) = log_a(x) - log_a(y)-对数函数的图像特点：- 自然对数函数ln(x)的图像是一个递增的曲线，该曲线通过点(1, 0)。

- 常用对数函数log(x)的图像也是一个递增的曲线，通过点(1, 0)。

它的曲线特点是较为陡峭，随着x的增加逐渐变缓。

4.对数函数的应用：对数函数在许多科学和工程领域中都有广泛的应用，主要包括以下几个方面。

-数据缩放和规范化：对数函数在数据处理中常用于对具有不同数量级的数据进行比较和处理，有助于减小数据之间的差异。

-扩大显示范围：当需要在同一图表中显示数量级相差较大的数据时，对数函数可以使得数据更加清晰可见。

-解方程：当指数方程难以求解时，可以将其转化为对数方程，并通过求解对数方程来得到解。

指数与对数函数指数与对数函数是高中数学中常见的函数类型，它们在数学和科学领域中具有广泛的应用。

指数函数可以用来表示增长的速度，而对数函数则可以用来解决指数式的问题。

本文将介绍指数与对数函数的定义、性质以及实际应用。

一、指数函数指数函数是一种以常数为底数的幂函数，它的一般形式可以表示为f(x) = a^x，其中a是正实数且不等于1。

指数函数的定义域为整个实数集，值域为正实数集。

指数函数的图像呈现出一种特殊的形态，即当底数大于1时，随着自变量增大，函数值也随之增大，呈现出递增趋势；而当底数小于1且大于0时，随着自变量增大，函数值反而减小，呈现出递减趋势。

指数函数在现实生活中有着广泛的应用。

举例来说，经济增长模型中常常使用指数函数来描述经济的增长趋势。

此外，放射性衰变也可以用指数函数来表示，指数函数在核物理领域起着重要的作用。

二、对数函数对数函数是指以某个正实数为底数，将正实数x映射到满足a^y = x的实数y的函数。

对数函数的定义域为正实数集，值域为整个实数集。

对数函数的一般形式可以表示为f(x) = logₐ(x)，其中a是正实数且不等于1。

对数函数与指数函数是互为反函数关系，即指数函数和对数函数的图像关于y=x对称。

对数函数的主要特点是，当底数大于1时，对数值随着自变量的增大而增大；当底数小于1且大于0时，对数值随着自变量的增大而减小。

对数函数广泛应用于科学和技术领域。

例如，在计算机科学中，对数函数在对数复杂性和算法分析中具有重要作用。

同时，在经济学和金融学中，对数函数常用于计算复利和持续增长的情况。

三、指数与对数函数的性质指数函数和对数函数具有一些重要的性质。

1. 指数与对数的互为反函数关系：对于任意的a>0且a≠1，和任意的x>0，有logₐ(a^x) = x和a^(logₐ(x)) = x。

也就是说，指数函数和对数函数是互为反函数的。

2. 指数与对数的运算规律：指数和对数具有一些重要的运算规律，如指数的乘方法则、指数函数的加法法则和对数的乘法法则等。

高中数学必会十大函数高中数学中有很多函数，但是有些函数是必须掌握的。

今天我们来讲一讲高中数学必会的十大函数。

1. 常数函数常数函数也叫恒等函数，它的函数表达式为f(x)=c，其中c是一个常数。

这个函数的图像是一条横线，因为它的y值并不会随着x的变化而变化。

2. 一次函数一次函数也叫线性函数，它的函数表达式为f(x)=kx+b，其中k 和b都是常数。

这个函数的图像是一条直线，它的斜率k表示函数的变化速率，截距b表示函数的纵截距。

3. 二次函数二次函数也叫抛物线函数，它的函数表达式为f(x)=ax²+bx+c，其中a、b和c都是常数，a≠0。

这个函数的图像是一条开口向上或向下的抛物线。

4. 幂函数幂函数的函数表达式为f(x)=xⁿ，其中n是一个整数。

这个函数的图像呈现的是不同的增长速度，正负的n决定了函数的单调性。

5. 指数函数指数函数的函数表达式为f(x)=aⁿ，其中a>0且a≠1，n是实数。

这个函数的图像呈现指数型增长或指数型衰减的趋势。

6. 对数函数对数函数是指数函数的反函数，它的函数表达式为f(x)=logaⁿ，其中a>0，且a≠1。

这个函数的图像呈现的是指数型下降或上升的趋势。

7. 三角函数三角函数包括正弦函数、余弦函数和正切函数等。

它们的图像都是一条连续的波浪线，而且都有周期性的变化，常常涉及到角度的概念。

8. 反三角函数反三角函数是三角函数的反函数，包括正弦函数的反函数、余弦函数的反函数和正切函数的反函数等。

这三个函数的图像是一条不连续的分段线段。

9. 双曲函数双曲函数包括双曲正弦函数、双曲余弦函数和双曲正切函数等。

这些函数的图像呈现的是一条连续的反比例函数曲线。

10. 拉布拉斯函数拉布拉斯函数是用于描述物理、工程等领域中的振动、波动等现象的数学函数。

这个函数的图像是一条连续的波浪线，类似于三角函数。

这些就是高中数学必会的十大函数。

通过学习这些函数，我们可以更好地了解和分析各种数学问题，并且能够在日常生活和工作中更好地应用数学知识。