无约束优化方法 坐标轮换法

《机械优化设计》§4-8 鲍威尔(Powell)方法¾基本思想：把n维无约束优化问题转化为n个沿坐标轴方向e 1,e 2……e n 的一维优化问题来求解。

坐标轮换法坐标轮换法：1e s x¾特点：z 方法简单，思路简明z 收敛速度太慢，效率太低鲍威尔算法的流程图{n次搜索判定并确定下轮方向组{构造新方向并一维搜索{计算条件参数准备信息判断终止条件5. 鲍威尔法的特点：（1）收敛速度快，可靠性高；（2）对非正定函数，也很有效；（3）计算步骤较复杂。

6. 鲍威尔法与坐标轮换法的主要区别：（1）每轮的搜索次数；（2）每轮的搜索方向组的构造方式。

0.01ε=的最优解。

迭代精度。

z例题（书P85）：用改进的鲍威尔法求目标函数22121212(,)10(5)()f x x x x x x =+−+−解：（一）第1轮迭代计算1）从出发，沿e 1方向进行一维搜索：(1)1100/22 4.5455α==得：(1)1[4.54550]T=x 初始点(1)0[00]T=x 12[10];[01]T T ==e e (1)(1)1120(5)20f ααα′=−+=min :(1)1()f x (1)0x (1)(1)(1)1011α=+x x e (1)2(1)2(1)11110(5)()()f ααα=−+=选取基本搜索方向组：(1)(1)1101;000αα⎡⎤⎡⎤⎡⎤=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2）从出发，沿e 2方向进行一维搜索：(1)20.826α=得：(1)2[4.54550.826]T=x (1)(1)2220(0.455)2( 4.545)0f ααα′=−+−=min :(1)(1)2(1)2(1)2222()10(4.5455)(4.545)()f f ααα=+−+−=x (1)1x (1)(1)(1)(1)21222(1)24.5454.5450;01ααα⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦xx e (1)2()15.215f =x (1)(1)212()()22.72715.2157.512f f Δ=−=−=x x 3）计算函数值以及下降量(1)0()250f =x (1)1()22.727f =x (1)(1)101()()25022.727227.27f f Δ=−=−=x x (1)()if x i Δ4）求最大下降量121max{,}227.723m Δ=ΔΔ=Δ=mΔ5）计算映射点及其函数值(1)()f x (1)x (1)(1)(1)24.545509.09220.82640 1.653⎡⎤⎡⎤⎡⎤=−=−=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x x (1)00()250F f ==x (1)()385.239f =x 6）计算判别条件式(1)22()15.215F f ==x (1)3()385.239F f ==x 30?F F <故不满足鲍威尔条件，则下一轮仍用原方向组。

无约束优化方法——坐标轮换法一.基本原理坐标轮换法是每次允许一个变量变化，其余变量保持不变，即沿坐标方向轮流进行搜索的寻优方法。

它把多变量的优化问题轮流的转化成单变量的优化问题，因此又称变量轮换法。

在搜索的过程中可以不需要目标函数的导数，只需目标函数值信息。

它比利用目标函数导数建立搜索方向的方法简单的多。

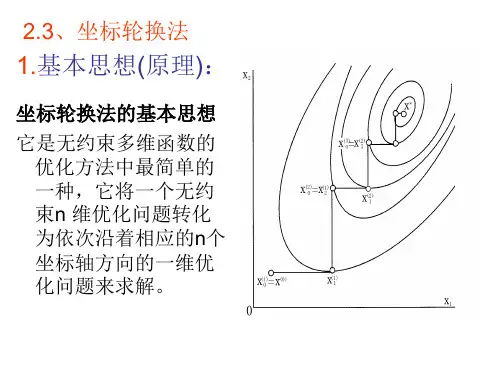
以二元函数飞f（x1,x2）为例说明坐标轮换法的寻优过程。

从初始点x00出发，沿第一个坐标方向搜索，即d10=e1得x10=x00+a01*d01按照一维搜索方法确定最佳步长因子a01满足minf(x00+a*d01),然后从x01出发沿d02=e2方向搜索得x02=x01+a02*d02,其中步长因子a02满足minf(x01+a*d02),x02为一轮（k=0）的终点。

检验始、终点之间的距离是否满足精度要求，即判断||x02-x00||<e的条件是否满足。

若满足则x*=x02,否则令x10=x02,重新一次沿坐标方向进行下一轮的搜索。

对于n个变量的函数，若在第k 轮沿第i个坐标方向dki进行搜索，其迭代公式为xki=xk(i-1)+aki+dki(k=0,1,2…,i=0,1,2…n)其中搜索方向取坐标方向，即dki=ei(i=1,…n)。

若||xkn-x00||<e,则x*=xkn,否则x(k+1)0=xkn,进行下一轮搜索，一直到满足精度为止。

注：上述xki中，其中k为上标，i为下标二．例题及程序1.用坐标轮换法求f(1x,2x)=10(1x+2x-5)^2+(1x-2x)^2极小值2.程序(1)function y=f(x)y=10*(x(1)+x(2)-5)^2+(x(1)-x(2))^2; ………………………..%定义f文件(2)d1=e1;syms a1;x1=x0+a1*d1;y1=f(x1);z1=diff(y1,a1);subs(z1);a1=solve(z1);%求沿e1方向最佳步长x1=x0+a1*d1;d2=e2;syms a2;x2=x1+a2*d2;y2=f(x2);z2=diff(y2,a2);subs(z2);a2=solve(z2);%求沿e2方向最佳步长x2=x1+a2*d2;m=x2-x0;m=double(m);t=norm(m); ……….%定义f2文件(3)x0=[0;0];e=0.001;e1=[1;0];e2=[0;1];f2; ………………%定义f3文件(4)f3;while (t>=e)x0=x2;f2;endx2=double(x2);xo=x2;xo…………………%定义f4文件三．程序框图四．计算结果及说明运用MATLAB运算结果如上所示，运算结果比较精确，跟课本上用鲍威尔方法计算结果比较相近。

第三章⽆约束最优化⽅法3第⼋节坐标轮换法把⼀个多维问题转化为⼀系列较少维数的问题称为降维。

降维⽅法有⼏种，坐标轮换法是⽤得较多的⼀种，这是⼀种不需要求函数导数的直接探索⽬标函数最优解的⽅法。

直接法、降维法⼀、坐标轮换法的基本思想其基本思想就是通过每次仅对多元函数的⼀个变量沿其坐标轴进⾏⼀维探索，其余各变量均固定不动，并依次轮换进⾏⼀维探索的坐标轴，完成第⼀轮探索后再重新进⾏第⼆轮探索，直到找到⽬标函数在全域上的最⼩点为⽌，以达到将⼀个多维的⽆约束最优化问题，转化为⼀系列的⼀维问题来求解的⽬的。

为简明起见，现以⼆元函数来说明基本步骤： 1.从初始点(0)(0)(0)(0)12(,,)n Xx x x =出发，依次沿各坐标轴⽅向搜索最优点，保持其余n-1个变量不变。

例：如果(0)(0)(0)(0)(0)123(,,,)(3,5,23,21)n Xx x x x ==，如果沿x 1轴⽅向搜索，则搜索过后改变的仅仅是x 1的值3，其余坐标的值均保持不变。

假设搜索到的值是8，则下⼀个点的值为(1)(1)(0)(0)(0)1123(,,,)(8,5,23,21)n X x x x x ==。

迭代点的序列为：(0)(1)(0)(0)(0)(0)0123(,,,)n X X x x x x →=(1)(1)(0)(0)(0)1123(,,,)n X x x x x = (1)(1)(1)(0)(0)2123(,,,)n X x x x x =(1)(1)(1)(1)(0)3123(,,,)n X x x x x =(1)(1)(1)(1)(1)(1)(2)1230(,,,)n n X x x x x X X =→→上标表⽰搜索的轮次，下标表⽰对应的坐标，亦即该轮次的第⼏次迭代。

经过⼀轮（n 次）迭代后，得到⼀个新点，然后进⾏下⼀轮迭代。

只到满⾜精度。

⼆、步长()k i α可以有以下⼏种取法1.随机选择()k iα值的⽅法2. 加速步长法为⽅向的初始试验了加快探索过程，可以采⽤加速步长法。

无约束优化上机指导一、实验目的利用无约束优化方法求目标函数的最优解。

无约束优化方法包括坐标轮换法、鲍威尔法、梯度法、牛顿法等。

二、方法及原理说明以二维无约束优化问题为例，说明坐标轮换法的原理：任意取一初始点(0)x 作为第一轮的起点(1)0x ，先沿第一坐标轴的方向1e ⎡⎤⎢⎥⎣⎦1=0作一维搜索，用一维优化方法确定其最优步长(1)1α，即可获得第一轮的第一个迭代点(1)(1)1011x x e α=+然后，以(1)1x 为新起点改沿第二坐标轴的方向201e ⎡⎤=⎢⎥⎣⎦作一维搜索，确定它的步长(1)2α，可得第一轮的第二个迭代点(1)(1)(1)2122x x e α=+这二维问题，经过两次一维搜索就完成了一轮迭代。

按终止准则进行检验()()0k k n x x e -≤满足精度则最优解取 *()k n x x =不满足则按同样的方法进行下一轮迭代。

流程图如下：三、实验内容用坐标轮换法求目标函数22121212()10460F x x x x x x x =+---+的无约束最优解。

给定初始点(0)00x ⎡⎤=⎢⎥⎣⎦，精度要求0.1e =解：该题为二维问题，单位坐标分别为1201e e ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦1=、0作第一轮迭代计算。

沿1e 方向进行一维搜索1(1)(1)1011101000x x e ααα⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦式中，(1)(0)0x x=为了求解1α，将(1)1x 点的值代入已知的目标函数，得1α的函数2111()1060F ααα=-+令11()0dF d αα=，即12100α-=，解得15α= 所以有，(1)(1)101150x x e α⎡⎤=+=⎢⎥⎣⎦以(1)1x 为新起点，沿2e 方向进行计算：(1)(1)21222255001xx e ααα⎡⎤⎡⎤⎡⎤=+=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦用求1α的方法同理求2α，得2 4.5α= 所以 (1)(1)212254.5xx e α⎡⎤=+=⎢⎥⎣⎦一轮计算中需要计算的点数与维数相等，故该轮计算中的两个点已计算完毕，对于第一轮按终止条件检验：(1)(1)20 6.70x x e -==>不满足精度要求，继续进行第二轮迭代计算。

无约束优化方法1.坐标轮换法2.鲍威尔法3.梯度法4.牛顿法5.变尺度法1.坐标轮换法坐标轮换发是一种不计算函数梯度,而是通过函数值本身,即可求出寻优方向,因而也称为直接寻优法.在以后提到的鲍威尔法(Powell)法也属于直接寻优法。

对于坐标轮换法，我们做个比喻：如果我们在北京的老城区找一个地方，我们可以沿着经纬线去找。

这个比喻为我们提供了一种思路，既可以取坐标的方向为寻优的方向，这就是坐标轮换法。

它在每次搜索中，只允许一个变量的变化，其余量保持不变，即沿着坐标方向轮流进行搜索的方法。

该方法把多变量的优化问题轮流转化成一系列单变量的优化问题。

对应于n 个变量的寻优函数，若在第轮沿第k 个坐标第i 个坐标方向ki i S e =进行搜索，则迭代公式为1(0,1,...,1,2,...,)k k k k i i i i X X S k i n α-=+==其中搜索方向取坐标方向，即k i i S e =（1,2,...,i n =）。

若0k k n X X -‖‖<ε，则*kn X X ←，否则10k kn X X +←，进行下一轮的搜索，一直到满足精度要求为止。

其搜索路径如图所示这种方法的收敛效果与目标函数等值线形有很大关系。

如果目标函数为二元二次函数，其等值线为圆或长轴平行于坐标轴的椭圆时，此方法很有效，经过两次搜索即可以达到最优点，如图所示。

如果等值线为长轴不平行于坐标轴的椭圆，则需多次迭代才能达到最优点，但因坐标轮换法是坐标方向搜索而不是沿脊线搜索，所以就终止到脊线上而不能找到最优解。

从上述分析可以看出，采用坐标轮换法只能轮流沿着坐标的方向搜索，尽管也能使函数值步步下降，但经过曲折迂回的路径才能达到极值点；尤其极值点附近步长很小，收敛很慢，所以坐标轮换法不是一种很好的搜索方法。

但是可以构造很好的搜索策略，下面讨论的鲍威尔法就是这种情况。

例题：已知22121212()10460f X x x x x x x =+---+，设初始点：(0)[0,0]T X=，精度0.1=ε，用最优步长法的坐标轮换法求目标函数的最优解。