中点模型的构造、等积模型

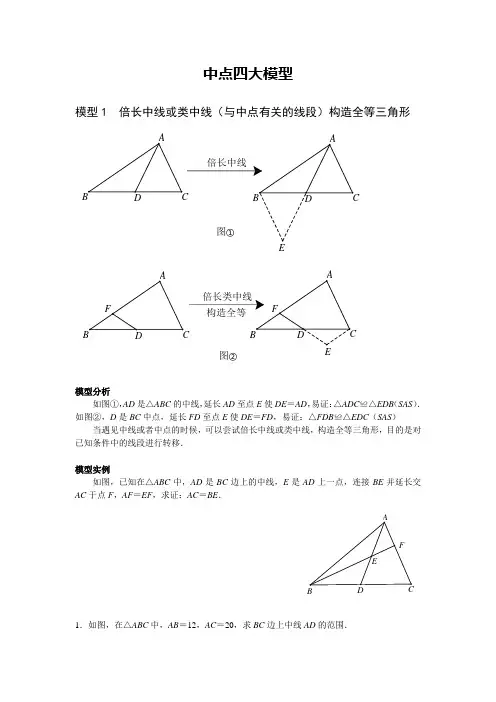
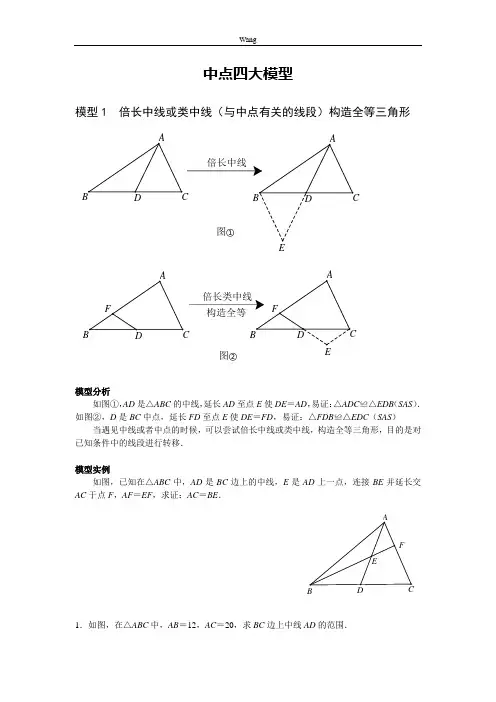
中点四大模型模型1 倍长中线或类中线（与中点有关的线段）构造全等三角形②图①图构造全等倍长类中线倍长中线DCBAFF ACABCDCA模型分析如图①，AD 是△ABC 的中线，延长AD 至点E 使DE ＝AD ，易证：△ADC ≌△EDB （SAS ）． 如图②，D 是BC 中点，延长FD 至点E 使DE ＝FD ，易证：△FDB ≌△EDC （SAS ）当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移．模型实例如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，连接BE 并延长交AC 于点F ，AF ＝EF ，求证：AC ＝BE ．FECA1．如图，在△ABC 中，AB ＝12，AC ＝20，求BC 边上中线AD 的范围．BA解：延长AD到E，使AD＝DE，连接BE，∵AD是△ABC的中线，∴BD＝CD，在△ADC与△EDB中，⎪⎩⎪⎨⎧=∠=∠=DEADBDEADCCDBD，∴△ADC≌△EDB（SAS），∴EB＝AC＝20，根据三角形的三边关系定理：20－12＜AE＜20＋12，∴4＜AD＜16，故AD的取值范围为4＜AD＜16．2．如图，在△ABC中，D是BC的中点，DM⊥DN，如果BM2＋CN2＝DM2＋DN2．求证：AD2＝41(AB2＋AC2)．NMD CA证明：如图，过点B作AC的平行线交ND的延长线于E，连ME．∵BD ＝DC ， ∴ED ＝DN ．在△BED 与△CND 中，∵⎪⎩⎪⎨⎧=∠=∠=DN ED CDN BDE DC BD ∴△BED ≌△CND （SAS ）． ∴BE ＝NC ． ∵∠MDN ＝90°，∴MD 为EN 的中垂线． ∴EM ＝MN ．∴BM 2＋BE 2＝BM 2＋NC 2＝MD 2＋DN 2＝MN 2＝EM 2， ∴△BEM 为直角三角形，∠MBE ＝90°． ∴∠ABC ＋∠ACB ＝∠ABC ＋∠EBC ＝90°． ∴∠BAC ＝90°． ∴AD 2＝(21BC )2＝41（AB 2＋AC 2）．模型2 已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．ABCDDCBA模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到： “边等、角等、三线合一”． 模型实例如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，M 为BC 的中点，MN ⊥AC 于点N ，求MN 的长度．NM CB A解答： 连接AM ．∵AB ＝AC ＝5，BC ＝6，点M 为BC 中点， ∴AM ⊥BC ，BM ＝CM ＝21BC ＝3． ∵AB ＝5， ∴AM ＝4352222=-=-BM AB ．∵MN ⊥AC ，∴S △ANC ＝21MC ·AM ＝21AC ·MN ． 即：21×3×4＝21×5×MN ．∴MN ＝512跟踪练习1．如图，在△ABC 中，AB ＝AC ，D 是BC 的中点，AE ⊥DE ，AF ⊥DF ，且AE ＝AF ，求证：∠EDB ＝∠FDC ．F证明：连结AD ，∵AB ＝AC ，D 是BC 的中点， ∴AD ⊥BC ，∠ADB ＝∠ADC ＝90° 在Rt △AED 与Rt △AFD 中，⎩⎨⎧==ADAD AFAB ， ∴Rt △AED ≌Rt △AFD ．（HL ） ∴∠ADE ＝∠ADF ， ∵∠ADB ＋∠ADC ＝90°， ∴∠EDB ＝∠FDC ．2．已知Rt △ABC 中，AC ＝BC ，∠C ＝90°，D 为AB 边的中点，∠EDF ＝90°，∠EDF 绕D 点旋转，它的两边分别交AC 、CB （或它们的延长线）于E 、F ．（1）当∠EDF 绕D 点旋转到DF ⊥AC 于E 时（如图①），求证：S △DEF ＋S △CEF ＝21S △ABC ； （2）当∠EDF 绕D 点旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立， S △DEF 、S △CEF 、S △ABC 又有怎样的数量关系？请写出你的猜想，不需要证明．③图②图①图ABDEFACDDCA解：（1）连接CD ；如图2所示： ∵AC ＝BC ，∠ACB ＝90°，D 为AB 中点， ∴∠B ＝45°，∠DCE ＝21∠ACB ＝45°，CD ⊥AB ，CD ＝21AB ＝BD ， ∴∠DCE ＝∠B ，∠CDB ＝90°，∵∠EDF ＝90°，∴∠1＝∠2，在△CDE 和△BDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠B DCB BD CD 21， ∴△CDE ≌△BDF （ASA ），∴S △DEF ＋S △CEF ＝S △ADE ＋S △BDF ＝21S △ABC ； （2）不成立；S △DEF −S △C EF ＝21S △ABC ；理由如下：连接CD ，如图3所示：同（1）得：△DEC ≌△DBF ，∠DCE ＝∠DBF ＝135° ∴S △DEF ＝S 五边形DBFEC ， ＝S △CFE ＋S △DBC ，＝S △CFE ＋21S △ABC ， ∴S △DEF －S △CFE ＝21S △ABC ．∴S △DEF 、S △CEF 、S △ABC 的关系是：S △DEF －S △CEF ＝21S △ABC ． 21ABCDE模型3 已知三角形一边的中点，可考虑中位线定理构造中位线取另一边中点EDDA模型分析在三角形中，如果有中点，可构造三角形的中位线，利用三角形中位线的性质定理：DE ∥BC ，且DE ＝21BC 来解题．中位线定理中既有线段之间的位置关系又有数量关系，该模型可以解决角问题，线段之间的倍半、相等及平行问题．模型实例如图，在四边形ABCD 中，AB ＝CD ，E 、F 分别是BC 、AD 的中点，连接EF 并延长，分别与BA 、CD 的延长线交于点M ，N ．求证：∠BME ＝∠CNE ．NM FEDCBA解答如图，连接BD ，取BD 的中点H ，连接HE 、HF ． ∵E 、F 分别是BC 、AD 的中点， ∴FH ＝21AB ，FH ∥AB ，HE ＝21DC ，HE ∥NC ． 又∵AB ＝CD ，∴HE ＝HF ．∴∠HFE ＝∠HEF ． ∵FH ∥MB ，HE ∥NC ，∴∠BME ＝∠HFE ，∠CNE ＝∠FEH ． ∴∠BME ＝∠CNE ．练习：1.（1）如图1，BD ，CE 分别是△ABC 的外角平分线，过点A 作AD ⊥BD ，AE ⊥CE ，垂足分别为D ，E ，连接DE ，求证：DE ∥BC ，DE =12（AB +BC +AC ）；（2）如图2，BD ，CE 分别是△ABC 的内角平分线，其他条件不变，上述结论是否成立？ （3）如图3，BD 是△ABC 的内角平分线，CE 是△ABC 的外角平分线，其他条件不变，DE 与BC 还平行吗？它与△ABC 三边又有怎样的数量关系？请写出你的猜想，并对其中一种情况进行证明.E D CBA图1G FEDCBA图2FED CBA图31.解答（1）如图①，分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌ △BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12HK .又∵HK =BK +BC +CH =AB +BC +AC . ∴DE =12（AB +AC +BC ）.（2）猜想结果：图②结论为DE =12（AB +AC -BC ） 证明：分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB同理可证，AE =HE ，AC =HC . ∴DE =12HK . 又∵HK =BK +CH -BC =AB +AC -BC∴DE =12（AB +AC -BC ）GABCDEKHF 图2（3）图③的结论为DE =12（BC +AC -AB ） 证明：分别延长AE ，AD 交BC 或延长线于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12KH . 又∵HK =BH -BK =BC +CH -BK =BC +AC -AB∴DE =12（BC +AC -AB ）.ABCD EKHF图32.问题一：如图①，在四边形ABCD 中，AB 与CD 相交于点O ，AB =CD ，E ，F 分别是BC ，AD 的中点，连接EF ，分别交DC ，AB 于点M ，N ，判断△OMN 的形状，请直接写出结论.问题二：如图②，在△ABC 中，AC >AB ，D 点在AC 上，AB =CD ，E ，F 分别是BC ，AD 的中点，连接EF 并延长，与BA 的延长线交于点G ，若∠EFC =60°，连接GD ，判断△AGD 的形状并证明.图1NMO F E DC BAE图2G ABCDF2.证明（1）等腰三角形（提示：取AC 中点H ，连接FH ，EH ，如图①）（2）△AGD 是直角三角形如图②，连接BD ，取BD 的中点H ，连接HF ，HE . ∵F 是AD 的中点， ∴HF ∥AB ，HF =12AB . ∴∠1=∠3.同理，HE ∥CD ，HE =12CD ， ∴∠2=∠EFC ， ∴AB =CD ， ∴HF =HE . ∴∠1=∠2.∵∠EFC =60°，∴∠3=∠EFC =∠AFG =60°. ∴△AGF 是等边三角形. ∴AF =FG . ∴GF =FD .∴∠FGD =∠FDG =30°.∴∠AGD =90°，即△AGD 是直角三角形.图2321G A BCDF H模型4 已知直角三角形斜边中点，可以考虑构造斜边中线DCBA模型分析在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半，即CD =12AB ，来证明线段间的数量关系，而且可以得到两个等腰三角形：△ACD 和△BCD ，该模型经常会与中位线定理一起综合应用. 模型实例如图，在△ABC 中，BE ，CF 分别为AC ，AB 上的高，D 为BC 的中点，DM ⊥ EF 于点M ，求证：FM =EM .M FEDCBA证明连接DE ，DF .BE ，CF 分别为边AC ，AB 上的高，D 为BC 的中点，DF =12BC ，DE =12BC .DF =DE ，即△DEF 是等腰三角形. DM ⊥EF ，点M 是EF 的中点，即FM =EM .ABCDEFM练习：1.如图，在△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB =10，求DM 的长度.1.解答取AB 中点N ，连接DN ，MN .在Rt △ADB 中，N 是斜边AB 上的中点， ∴DN =12AB =BN =5.∴∠NDB =∠B .在△ABC 中，M ，N 分别是BC ，AB 的中点， ∴MN ∥AC∴∠NMB =∠C ，又∵∠NDB 是△NDM 的外角， ∴∠NDB =∠NMD +∠DNM .即∠B =∠NMD +∠DNM =∠C +∠DNM . 又∵∠B =2∠C ，∴∠DNM =∠C =∠NMD . ∴DM =DN . ∴DM =5.N MD CBA2.已知，△ABD 和△ACE 都是直角三角形，且∠ABD =∠ACE =90°，连接DE ，M 为DE 的中点，连接MB ，MC ，求证：MB =MC .MEDCBA2.证明延长BM 交CE 于G ，∵△ABD 和△ACE 都是直角三角形， ∴CE ∥BD .∴∠BDM =∠GEM .又∵M 是DE 中点，即DM =EM ， 且∠BMD =∠GME ， ∴△BMD ≌△GME . ∴BM =MG .∴M 是BG 的中点，∴在Rt △CBG 中，BM =CM .3.问题1：如图①，三角形ABC 中，点D 是AB 边的中点，AE ⊥ BC ，BF ⊥AC ，垂足分别为点E ，F .AE 、BF 交于点M ，连接DE ，DF ，若DE =kDF ，则k 的值为 . 问题2：如图②，三角形ABC 中，CB =CA ，点D 是AB 边的中点，点M 在三角形ABC 内部，且∠MAC =∠MBC ，过点M 分别作ME ⊥BC ，MF ⊥ AC ，垂足分别为点E ，F ，连接DE ，DF ，求证：DE =DF .问题3：如图③，若将上面问题2中的条件“CB =CA ”变为“CB ≠CA ”，其他 条件不变，试探究DE 与DF 之间的数量关系，并证明你的结论.图1MF DCBA图2ABCDE FM图3ABCDF M3.解答∵（1）AE ⊥BC ，BF ⊥AC ，∴△AEB 和△AFB 都是直角三角形， ∵D 是AB 的中点， ∴DE =12AB ，DF =12AB .∴DE =DF . ∵DE =KDF ， ∴k =1. （2）∵CB =CA ， ∴∠CBA =∠CAB . ∵∠MAC =∠MBC ，∴∠CBA -∠MBC =∠CAB -∠MAC ，即∠ABM =∠BAM . ∴AM =BM .∵ME ⊥BC ，MF ⊥AC ， ∴∠MEB =∠MF A =90°. 又∵∠MBE =∠MAF ，∴△MEB ≌△MF A （AAS ） ∴BE =AF .∵D 是AB 的中点，即BD =AD ， 又∵∠DBE =∠DAF ，∴△DBE ≌△DAF （SAS ） ∴DE =DF .（3）DE =DF .图1M F E DCB A如图，作AM的中点G，BM的中点H，连DG，FG，DH，EH. ∵点D是边AB的中点，∴DG∥BM，DG=12 BM.同理可得：DH∥AM，DH=12AM.∵ME⊥BC于E，H是BM的中点.∴在Rt△BEM中，HE=12BM=BH.∴∠HBE=∠HEB.∴∠MHE=2∠HBE.又∵DG=12BM，HE=12BM，∴DG=HE.同理可得：DH=FG. ∠MGF=2∠MAC.∵DG∥BM，DH∥GM，∴四边形DHMG是平行四边形.∴∠DGM=∠DHM.∵∠MGF=2∠MAC，∠MHE=2∠MBC，∠MBC=∠MAC，∴∠MGF=∠MHE.∴∠DGM+∠MGF=∠DHM+∠MHE.∴∠DGF=∠DHE.在△DHE与△FGD中DG HEDGF DHEDH FG=⎧⎪∠=∠⎨⎪=⎩∴△DHE≌△FGD（SAS）∴DE=DF.图2AB CDEFM。

几何综合题型一：中点模型的构造中点模型 ①中线（点）：倍长（类）中线 ②两中点：中位线③等腰三角形底边中点：三线合一④直角三角形斜边中点：斜边中线=斜边一半⇒构造两等腰 ⑤中垂线：中垂线上的点连两端点有些题目的中点没有直接给出，此时需要挖掘题目中隐含的中点条件，并适时添加辅助线．典题精练【例1】 如图，在平行四边形ABCD 中，点M 为边AD 的中点，过点C 作AB 的垂线交AB 于点E ，若∠EMD = 3∠MEA ．求证：BC =2AB ．DCBA E M【解析】证法一：如右图（a ），延长EM 交CD 的长线于点E '，连结CM ∵AB ∥CD ，∴∠ME'D =∠MEA ．又AM = DM ，∠AME =∠DME' ∴△AFM ≌△DE M '． ∴EM =E M '∵AB ∥CD ，CE ⊥AB ， ∴EC ⊥CD ．∴CM 是Rt △ECE '斜边EE '的中线， ∴ME '=MC ．∴ME D E CM '='，∴∠EMC = 2ME D ∠'= 2∠AEM ． ∵∠EMD =3∠MEA ， ∴∠CMD =∠DCM ， ∴MD = CD ．∵AD = 2DM ，AB = CD ，AD = BC ， ∴BC = 2AB ．证法二：(a )E’ME A BCD如右图(b )，过点M 作MM AB '∥交BC 于M '，过点M '作M E ME ''∥交AB 的延长线于点E '，连接EM '．∴点M '是BC '的中点，EE AB '=，E BM EAM ∠''=∠，M E B M EA ''=∠，M MD EAM E BM '=∠=∠'' ∵点M '是Rt △EBC 斜边BC 的中点， ∴M E BM '='，∴BEM M BE ∠'=∠'．∴180E BM BEM ∠''=︒-∠'．∵∠EMD = 3∠MEA ，∴2M MD MEA ∠'=∠， ∴2E BM M E B ∠''=∠''∴1802BEM M E B ︒-∠'=∠''，1902M E B BEM ∠''=︒-∠'．∴E EM E ∠=∠''．∴EM EE '=',∴BM AB '=． ∴BC = 2AB ．【例2】 如图所示，分别以△ABC 的边AB 、AC 为边，向三角形的外侧作正方形ABDE 和正方形ACFG ，点M 为BC 中点，⑴ 求证：AM ⊥EG ；⑵ 求证：EG = 2AM ．GF E DCBAM【解析】⑴ 如图所示，延长AM 到N ，使MN = AM ,延长MA 交EG 于点P ，连接BN 、NC ．∵BM = CM ，∴四边形ABNC 是平行四边形． ∴BN = AC = AG ．∵∠EAG +∠BAC = 180︒， ∠ABN +∠BAC = 180︒， ∴∠EAG =∠ABN ． ∵AE = AB ，∴△EAG ≌△ABN ．∴∠AEG =∠BAN ． 又∵∠EAB = 90︒，∴∠EAP +∠BAN = 90︒． ∴∠AEP +∠EAP = 90︒． ∴MA ⊥EG ．⑵ 证明：∵△EAG ≌△ABN ，∴EG = AN = 2AM ．题型二：平移及等积变换典题精练(b )M’E’ME A B CDN P M A B C DE F G【例3】 已知：如图，正方形ABCD 中，E 是AB 上一点，FG ⊥DE 于点H ．⑴ 求证：FG = DE ．⑵ 求证：FD + BG．HG FE DC B APAB C DEFG H【解析】延长GC 到点P ，使得GP = DF ，连接EP ，DP ．⑴ ∵DF ∥GP ，GP = DF∴四边形DFGP 为平行四边形 ∴FG = DP ，FG ∥DP 又∵FG ⊥DE ，∴DP ⊥DE ∴∠ADE =∠CDP 在△ADE 和△CDP 中 DAE DCP DA DCADE CDP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CDP ∴DE = DP = FG⑵ 由⑴知道△DEP 为等腰直角三角形∴EP ==在△EGP 中，EG + DF = EG + GP ≥PE当EG ∥FD 时，取到等号【例4】 如下图，过平行四边形ABCD 内的一点P 作边的平行线EF 、GH ，若△PBD 的面积为8平方分米，求平行四边形PHCF 的面积比平行四边形PGAE 的面积大多少平方分米？D【解析】根据差不变原理，要求平行四边形PHCF 的面积与平行四边形PGAE 的面积差，相当于求平行四边形BCFE 的面积与平行四边形ABHG 的面积差． 如右图，连接CP 、AP ．可得：12BCP ADP S S ABCD +=△△12ABP BDP ADP ABCD S S S S ++=△△△所以BCD ABP BDP S S S -=△△△而12BCP BCFE S S =△，12ABP ABHG S S =△，所以()2216BCFE ABHG BCP ABP BDP S S S S S -=-==△△△(平方分米)．题型三：旋转典题精练【例5】 已知△ABC 和△ADE 都是等腰直角三角形,∠ABC =∠ADE =90°，点M 是CE 的中点，连接BM .⑴ 如图①，点D 在AB 上，连接DM ，并延长DM 交BC 于点N ，可探究得出BD 与BM 的数量关系为 ．⑵ 如图②，点D 不在AB 上，⑴中的结论还成立吗？如果成立，请证明；如果不成立，说明理由．图1NMED CBA图2M DCBE【解析】⑴ BD⑵ 结论成立，证明：连接DM ，过点C 作CF ∥ED ，与DM 的延长线交于点F ，连接BF ，可证得△MDE ≌△MFC ,∴DM = FM ，DE = FC ， ∴AD = ED = FC ， 作AN ⊥EC 于点N ，由已知∠ADE =90°，∠ABC =90°， 可证得∠1 =∠2，∠3 =∠4， ∵CF ∥ED ， ∴∠1 =∠FCM ，∴∠BCF =∠4 +∠FCM = ∠3 +∠1 =∠3 +∠2 =∠BAD . ∴△BCF ≌△BAD ,∴BF = BD ，∠5 =∠6，∴∠DBF =∠5 +∠ABF =∠6 +∠ABF =∠ABC = 90°， ∴△DBF 是等腰三角形， ∵点M 是DF 的中点， 则△BMD 是等腰三角形，∴BD【例6】 已知正方形ABCD ，在BC 边上取一点E ，作EF AE ⊥交BCD ∠的外角平分线于F ，求证：AE EF =．D F CE B AGDFCE BA 【解析】 法一：如图，连接AC ，过E 作EG BC ⊥，交AC 于G ．∵90AEG GEF ∠=︒-∠，90FEC GEF ∠=︒-∠， ∴AEG FEC ∠=∠．又∵GEC △为等腰直角三角形，∴GE CE =．又9045135ECF ∠=︒+︒=︒，18045135EGA ∠=︒-︒=︒， ∴ECF EGA ∠=∠，∴AEG FEC △≌△，故AE EF =． 法二：如图，过E 作EG BC ⊥，交FC 的延长线于G ，连接AC ， 则45ECG DCF ∠=∠=︒，∴45EGF ∠=︒，∴EG EC =．而45ACE ∠=︒，∴EGF ECA ∠=∠．又90FEG FEC ∠=︒+∠，90AEC FEC ∠=︒+∠，∴FEG AEC ∠=∠，有EFG EAC △≌△， ∴AE EF =．法三：在AB 上截取BN =BE ，证明ANE ECF △≌△即可；思维拓展训练(选讲)训练1. 如图所示 ，等腰梯形ABCD 中，AB ∥CD ，AD = BC ，AC 与BD 交于点O ，∠AOB =60︒，P 、Q 、R 分别是OA 、OB 、OC 的中点，求证：△PQR 是正三角形．DCB AR Q P O【解析】证明：如右图，连接BP 、CR ．∵四边形ABCD 是等腰梯形， ∴AD = BC ，OA = OB ，OC = OD ． ∵∠AOB = 60°，∴△AOB 、△COD 都是正三角形． ∵P 是OA 的中点，R 是OD 的中点， ∴BP ⊥OA ，CR ⊥OD ． ∵PR 是△ODA 的中位线，∴PR = 1122AD BC =．∴PR = PQ = QR ．GDFCE BAO P QR ABCD∴△PQR 是正三角形．训练2. 如图⑴，四边形EFGH 中，若12∠=∠，则3∠必然等于4∠．请运用结论证明下述问题：如图⑵，在平行四边形ABCD 中取一点P ，使得56∠=∠，求证：78∠=∠．4321HGE F (1)(2)A BCDP5678【分析】此题为信息题，难点在于如何理解已知条件，经观察我们．．．．．发现，若．．．．1∠和．2∠，位置为．．．．时可得出．．．．3∠和．4∠相等．．（．本质为．．．四点共圆．．．．）．．图⑵中，5∠与6∠关系并不像条件所示，因此，需要改变角位置，而这点可以通过构造平行四边形来解决．而构造平行四边形，恰可以达到改变角位置作用，为使5∠与6∠成形，我们可有如下四种方法．【解析】分别过点B 、P 作BK AP ∥，PK AB ∥，交于点K ，连接CK ．∵BK AP ∥，PK AB ∥∴BK AP =，PK AB =，5BKP ∠=∠，7BPK ∠=∠∵AB CD =，AB CD ∥ ∴PK CD ∥，PK CD =∴四边形PKCD 为平行四边形 ∴PD CK = ∵AD BC = ∴ADP △≌BCK △∴8BCK ∠=∠ 在四边形BKCP 中，56BKP ∠=∠=∠ ∴BPK BCK ∠=∠ ∴78∠=∠A BCDP 5678K(∠5,∠6不动移)A BCDP 5678K(∠5,∠6不动移)ABC D P5678K(∠5不动移∠6)（∠5不动移∠6） （∠5，∠6不移动） （∠5，∠6不移动）(∠6不动移∠5)K8765P DC B A训练3. 已知：在△ABC 中，BC = a ，AC = b ，以AB 为边作等边三角形ABD ．探究下列问题：⑴ 如图(a )，当点D 与点C 位于直线AB 的两侧时，a = b = 3，且∠ACB =60°，则CD = ________；⑵ 如图(b )，当点D 与点C 位于直线AB 的同侧时，a = b = 6，且∠ACB =90°，则CD = ________；⑶ 如图(c )，当∠ACB 变化，且点D 与点C 位于直线AB 的两侧时，求CD 的最大值及相应的∠ACB 的度数．(a )D C BA(b )DCBA(c )ABCD【解析】⑴⑵⑶ 如图（d ），以点D 为中心，将△DBC 逆时针旋转60°，则点B 落在点A ，点C 落在点E ，连接AE 、CE 、DE ． ∴CD = ED ，∠CDE = 60°． ∴△CDE 为等边三角形． ∴CE = CD ．当点E 、A 、C 不在一条直线上时，有CD = CE < AE + AC = a + b ；如图(e ),当点E 、A 、C 在一条直线上时，CD 有最大值，CD = CE = a + b ； 此时∠CED =∠BCD =∠ECD =60°，∴∠ACB =120°． 因此当∠ACB =120°时，CD 有最大值是a + b ．ED CBA(d )(e )ED CBA。

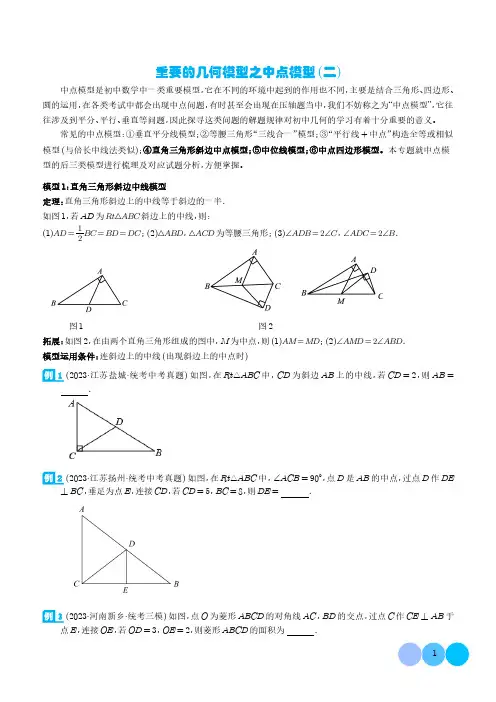
重要的几何模型之中点模型(二)中点模型是初中数学中一类重要模型，它在不同的环境中起到的作用也不同，主要是结合三角形、四边形、圆的运用，在各类考试中都会出现中点问题，有时甚至会出现在压轴题当中，我们不妨称之为“中点模型”，它往往涉及到平分、平行、垂直等问题，因此探寻这类问题的解题规律对初中几何的学习有着十分重要的意义。

常见的中点模型：①垂直平分线模型；②等腰三角形“三线合一”模型；③“平行线+中点”构造全等或相似模型(与倍长中线法类似)；④直角三角形斜边中点模型；⑤中位线模型；⑥中点四边形模型。

本专题就中点模型的后三类模型进行梳理及对应试题分析，方便掌握。

模型1：直角三角形斜边中线模型定理：直角三角形斜边上的中线等于斜边的一半．如图1，若AD为Rt△ABC斜边上的中线，则：(1)AD=1BC=BD=DC；(2)△ABD，△ACD为等腰三角形；(3)∠ADB=2∠C，∠ADC=2∠B．2图1图2拓展：如图2，在由两个直角三角形组成的图中，M为中点，则(1)AM=MD；(2)∠AMD=2∠ABD．模型运用条件：连斜边上的中线(出现斜边上的中点时)1(2023·江苏盐城·统考中考真题)如图，在Rt△ABC中，CD为斜边AB上的中线，若CD=2，则AB=．2(2023·江苏扬州·统考中考真题)如图，在Rt△ABC中，∠ACB=90°，点D是AB的中点，过点D作DE ⊥BC，垂足为点E，连接CD，若CD=5，BC=8，则DE=．3(2023·河南新乡·统考三模)如图，点O为菱形ABCD的对角线AC，BD的交点，过点C作CE⊥AB于点E，连接OE，若OD=3，OE=2，则菱形ABCD的面积为．4(2023上·四川成都·九年级校考期中)如图，四边形ABCD中，∠ABC=∠ADC=90°，∠BAD=45°，连接AC、BD．M是AC的中点，连接BM、DM．若AC=10，则△BMD的面积为．5(2023·江苏常州·中考真题)如图，AB是⊙O的弦，点C是优弧AB上的动点(C不与A、B重合)，CH⊥AB，垂足为H，点M是BC的中点．若⊙O的半径是3，则MH长的最大值是()A.3B.4C.5D.66(2023·辽宁鞍山·校考三模)如图，在Rt△ABC中，∠ABC=90°，∠ACB=30°，将△ABC绕点C顺时针旋转60°得到△DEC，点A，B的对应点分别是D，E，点F是边AC的中点，连接BF，BE，FD，则下列说法不正确的是()A.BE=BCB.∠DFC=90°C.DG=3GFD.四边形BFDE是平行四边形模型2：中位线模型三角形的中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。

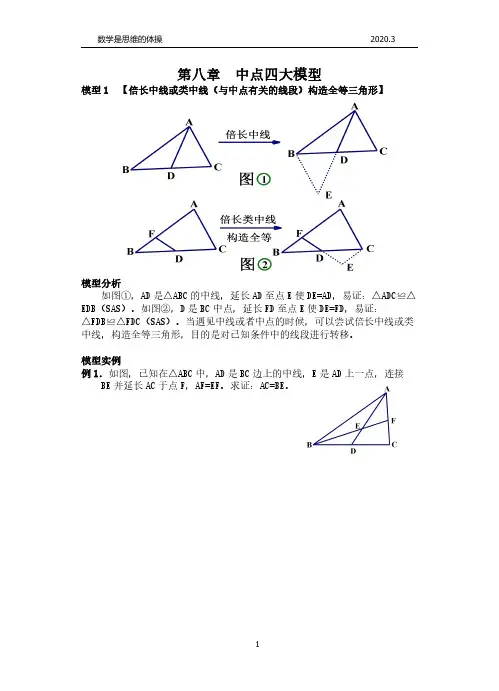
第八章中点四大模型模型1【倍长中线或类中线（与中点有关的线段）构造全等三角形】模型分析如图①，AD是△ABC的中线，延长AD至点E使DE=AD，易证：△ADC≌△EDB（SAS）。

如图②，D是BC中点，延长FD至点E使DE=FD，易证：△FDB≌△FDC（SAS）。

当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移。

模型实例例1．如图，已知在△ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长AC于点F，AF=EF。

求证：AC=BE。

热搜精练1．如图，在△ABC 中，AB=12，AC=20，求BC 边上中线AD 的范围。

2．如图，在△ABC 中，D 是BC 的中点，DM⊥DN，如果2222B M C N D M D N +=+。

求证：()22214A D AB AC =+。

模型2【已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”】模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等或边相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到：“边等、角等、三线合一”。

模型实例例1．如图，在△ABC中，AB=AC-5，BC=6，M为BC的中点，MN⊥AC于点N，求MN的长度。

热搜精练1．如图，在△ABC中，AB=AC，D是BC的中点，AE⊥DE，AF⊥DF，且AE=AF。

求证：∠EDB=∠FDC。

2．已知Rt△ABC 中，AC=BC，∠C=90°，D 为AB 边的中点，∠EDF=90°，∠EDF 绕点D 旋转，它的两边分别交AC、CB（或它们的延长线）于E、F。

（1）当∠EDF 绕点D 旋转到DE⊥AC 于E 时（如图①），求证：12DEF CEF ABC S S S += ；（2）当∠EDF 绕点D 旋转到DE 和AC 不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，DEF S 、CEF S 、ABC S 又有怎样的数量关系？请写出你的猜想，不需证明。

中点四大模型模型1 倍长中线或类中线（与中点有关的线段）构造全等三角形②图①图构造全等倍长类中线倍长中线DCBAFF ACABCDCA模型分析如图①，AD 是△ABC 的中线，延长AD 至点E 使DE ＝AD ，易证：△ADC ≌△EDB （SAS ）． 如图②，D 是BC 中点，延长FD 至点E 使DE ＝FD ，易证：△FDB ≌△EDC （SAS ）当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移．模型实例如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，连接BE 并延长交AC 于点F ，AF ＝EF ，求证：AC ＝BE ．FECA1．如图，在△ABC 中，AB ＝12，AC ＝20，求BC 边上中线AD 的范围．BA解：延长AD到E，使AD＝DE，连接BE，∵AD是△ABC的中线，∴BD＝CD，在△ADC与△EDB中，⎪⎩⎪⎨⎧=∠=∠=DEADBDEADCCDBD，∴△ADC≌△EDB（SAS），∴EB＝AC＝20，根据三角形的三边关系定理：20－12＜AE＜20＋12，∴4＜AD＜16，故AD的取值范围为4＜AD＜16．2．如图，在△ABC中，D是BC的中点，DM⊥DN，如果BM2＋CN2＝DM2＋DN2．求证：AD2＝41(AB2＋AC2)．NMD CA证明：如图，过点B作AC的平行线交ND的延长线于E，连ME．∵BD＝DC，∴ED＝DN．在△BED与△CND中，∵⎪⎩⎪⎨⎧=∠=∠=DNEDCDNBDEDCBD∴△BED≌△CND（SAS）．∴BE＝NC．∵∠MDN＝90°，∴MD为EN的中垂线．∴EM＝MN．∴BM2＋BE2＝BM2＋NC2＝MD2＋DN2＝MN2＝EM2，∴△BEM为直角三角形，∠MBE＝90°．∴∠ABC＋∠ACB＝∠ABC＋∠EBC＝90°．∴∠BAC＝90°．∴AD2＝(21BC)2＝41（AB2＋AC2）．模型2 已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”．AB CDD CBA模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到： “边等、角等、三线合一”． 模型实例如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，M 为BC 的中点，MN ⊥AC 于点N ，求MN 的长度．NM CB A解答： 连接AM ．∵AB ＝AC ＝5，BC ＝6，点M 为BC 中点， ∴AM ⊥BC ，BM ＝CM ＝21BC ＝3． ∵AB ＝5， ∴AM ＝4352222=-=-BM AB ．∵MN ⊥AC ，∴S △ANC ＝21MC ·AM ＝21AC ·MN ． 即：21×3×4＝21×5×MN ．∴MN ＝512跟踪练习1．如图，在△ABC 中，AB ＝AC ，D 是BC 的中点，AE ⊥DE ，AF ⊥DF ，且AE ＝AF ，求证：∠EDB ＝∠FDC ．F证明：连结AD ，∵AB＝AC，D是BC的中点，∴AD⊥BC，∠ADB＝∠ADC＝90°在Rt△AED与Rt△AFD中，⎩⎨⎧==ADADAFAB，∴Rt△AED≌Rt△AFD．（HL）∴∠ADE＝∠ADF，∵∠ADB＋∠ADC＝90°，∴∠EDB＝∠FDC．2．已知Rt△ABC中，AC＝BC，∠C＝90°，D为AB边的中点，∠EDF＝90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．（1）当∠EDF绕D点旋转到DF⊥AC于E时（如图①），求证：S△DEF＋S△CEF＝21S△ABC；（2）当∠EDF绕D点旋转到DE和AC不垂直时，在图②和图③这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需要证明．③图②图①图ABDEFACDDCA解：（1）连接CD；如图2所示：∵AC＝BC，∠ACB＝90°，D为AB中点，∴∠B＝45°，∠DCE＝21∠ACB＝45°，CD⊥AB，CD＝21AB＝BD，∴∠DCE＝∠B，∠CDB＝90°，∵∠EDF＝90°，∴∠1＝∠2，在△CDE 和△BDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠B DCB BD CD 21， ∴△CDE ≌△BDF （ASA ），∴S △DEF ＋S △CEF ＝S △ADE ＋S △BDF ＝21S △ABC ； （2）不成立；S △DEF −S △C EF ＝21S △ABC ；理由如下：连接CD ，如图3所示：同（1）得：△DEC ≌△DBF ，∠DCE ＝∠DBF ＝135° ∴S △DEF ＝S 五边形DBFEC ， ＝S △CFE ＋S △DBC ，＝S △CFE ＋21S △ABC ， ∴S △DEF －S △CFE ＝21S △ABC ．∴S △DEF 、S △CEF 、S △ABC 的关系是：S △DEF －S △CEF ＝21S △ABC ． 21ABCDE模型3 已知三角形一边的中点，可考虑中位线定理构造中位线取另一边中点EDDA模型分析在三角形中，如果有中点，可构造三角形的中位线，利用三角形中位线的性质定理：DE ∥BC ，且DE ＝21BC 来解题．中位线定理中既有线段之间的位置关系又有数量关系，该模型可以解决角问题，线段之间的倍半、相等及平行问题．模型实例如图，在四边形ABCD 中，AB ＝CD ，E 、F 分别是BC 、AD 的中点，连接EF 并延长，分别与BA 、CD 的延长线交于点M ，N ．求证：∠BME ＝∠CNE ．NM FEDCBA解答如图，连接BD ，取BD 的中点H ，连接HE 、HF ． ∵E 、F 分别是BC 、AD 的中点， ∴FH ＝21AB ，FH ∥AB ，HE ＝21DC ，HE ∥NC ． 又∵AB ＝CD ，∴HE ＝HF ．∴∠HFE ＝∠HEF ． ∵FH ∥MB ，HE ∥NC ，∴∠BME ＝∠HFE ，∠CNE ＝∠FEH ． ∴∠BME ＝∠CNE ．练习：1.（1）如图1，BD ，CE 分别是△ABC 的外角平分线，过点A 作AD ⊥BD ，AE ⊥CE ，垂足分别为D ，E ，连接DE ，求证：DE ∥BC ，DE =12（AB +BC +AC ）；（2）如图2，BD ，CE 分别是△ABC 的内角平分线，其他条件不变，上述结论是否成立？ （3）如图3，BD 是△ABC 的内角平分线，CE 是△ABC 的外角平分线，其他条件不变，DE 与BC 还平行吗？它与△ABC 三边又有怎样的数量关系？请写出你的猜想，并对其中一种情况进行证明.E D CBA图1G FEDCBA图2FED CBA图31.解答（1）如图①，分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌ △BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12HK .又∵HK =BK +BC +CH =AB +BC +AC . ∴DE =12（AB +AC +BC ）.（2）猜想结果：图②结论为DE =12（AB +AC -BC ） 证明：分别延长AE ，AD 交BC 于H ，K . 在△BAD 和△BKD 中ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB同理可证，AE =HE ，AC =HC . ∴DE =12HK . 又∵HK =BK +CH -BC =AB +AC -BC∴DE =12（AB +AC -BC ）GABCDEKHF 图2（3）图③的结论为DE =12（BC +AC -AB ） 证明：分别延长AE ，AD 交BC 或延长线于H ，K . 在△BAD 和△BKD 中，ABD DBK BD BDBDA BDK ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BAD ≌△BKD （ASA ） ∴AD =KD ，AB =KB .同理可证，AE =HE ，AC =HC . ∴DE =12KH . 又∵HK =BH -BK =BC +CH -BK =BC +AC -AB∴DE =12（BC +AC -AB ）.AB CDEK HF图32.问题一：如图①，在四边形ABCD中，AB与CD相交于点O，AB=CD，E，F分别是BC，AD的中点，连接EF，分别交DC，AB于点M，N，判断△OMN的形状，请直接写出结论.问题二：如图②，在△ABC中，AC>AB，D点在AC上，AB=CD，E，F分别是BC，AD的中点，连接EF并延长，与BA的延长线交于点G，若∠EFC=60°，连接GD，判断△AGD 的形状并证明.图1NMOFEDCBAE图2GAB CDF2.证明（1）等腰三角形（提示：取AC中点H，连接FH，EH，如图①）（2）△AGD是直角三角形如图②，连接BD，取BD的中点H，连接HF，HE.∵F是AD的中点，∴HF∥AB，HF=12AB.∴∠1=∠3.同理，HE∥CD，HE=12CD，∴∠2=∠EFC，∴AB=CD，∴HF=HE.∴∠1=∠2.∵∠EFC =60°，∴∠3=∠EFC =∠AFG =60°. ∴△AGF 是等边三角形. ∴AF =FG . ∴GF =FD .∴∠FGD =∠FDG =30°.∴∠AGD =90°，即△AGD 是直角三角形.图2321G A BCDF H模型4 已知直角三角形斜边中点，可以考虑构造斜边中线DCBA模型分析在直角三角形中，当遇见斜边中点时，经常会作斜边上的中线，利用直角三角形斜边上的中线等于斜边的一半，即CD =12AB ，来证明线段间的数量关系，而且可以得到两个等腰三角形：△ACD 和△BCD ，该模型经常会与中位线定理一起综合应用. 模型实例如图，在△ABC 中，BE ，CF 分别为AC ，AB 上的高，D 为BC 的中点，DM ⊥ EF 于点M ，求证：FM =EM .M FEDCBA证明连接DE ，DF .BE ，CF 分别为边AC ，AB 上的高，D 为BC 的中点，DF =12BC ，DE =12BC .DF =DE ，即△DEF 是等腰三角形. DM ⊥EF ，点M 是EF 的中点，即FM =EM .ABCDEFM练习：1.如图，在△ABC 中，∠B =2∠C ，AD ⊥BC 于D ，M 为BC 的中点，AB =10，求DM 的长度.1.解答取AB 中点N ，连接DN ，MN .在Rt △ADB 中，N 是斜边AB 上的中点， ∴DN =12AB =BN =5.∴∠NDB =∠B .在△ABC 中，M ，N 分别是BC ，AB 的中点， ∴MN ∥AC∴∠NMB =∠C ，又∵∠NDB 是△NDM 的外角， ∴∠NDB =∠NMD +∠DNM .即∠B =∠NMD +∠DNM =∠C +∠DNM . 又∵∠B =2∠C ，∴∠DNM =∠C =∠NMD . ∴DM =DN . ∴DM =5.N MD CBA2.已知，△ABD 和△ACE 都是直角三角形，且∠ABD =∠ACE =90°，连接DE ，M 为DE 的中点，连接MB ，MC ，求证：MB =MC .MEDCBA2.证明延长BM 交CE 于G ，∵△ABD 和△ACE 都是直角三角形， ∴CE ∥BD .∴∠BDM =∠GEM .又∵M 是DE 中点，即DM =EM ， 且∠BMD =∠GME ， ∴△BMD ≌△GME . ∴BM =MG .∴M 是BG 的中点，∴在Rt △CBG 中，BM =CM .3.问题1：如图①，三角形ABC 中，点D 是AB 边的中点，AE ⊥ BC ，BF ⊥AC ，垂足分别为点E ，F .AE 、BF 交于点M ，连接DE ，DF ，若DE =kDF ，则k 的值为 . 问题2：如图②，三角形ABC 中，CB =CA ，点D 是AB 边的中点，点M 在三角形ABC 内部，且∠MAC =∠MBC ，过点M 分别作ME ⊥BC ，MF ⊥ AC ，垂足分别为点E ，F ，连接DE ，DF ，求证：DE =DF .问题3：如图③，若将上面问题2中的条件“CB =CA ”变为“CB ≠CA ”，其他 条件不变，试探究DE 与DF 之间的数量关系，并证明你的结论.图1MF E DCBA图2ABCDFM图3ABCDF M3.解答∵（1）AE ⊥BC ，BF ⊥AC ，∴△AEB 和△AFB 都是直角三角形， ∵D 是AB 的中点， ∴DE =12AB ，DF =12AB .∴DE =DF . ∵DE =KDF ， ∴k =1. （2）∵CB =CA ， ∴∠CBA =∠CAB . ∵∠MAC =∠MBC ，∴∠CBA -∠MBC =∠CAB -∠MAC ，即∠ABM =∠BAM . ∴AM =BM .∵ME ⊥BC ，MF ⊥AC ， ∴∠MEB =∠MF A =90°. 又∵∠MBE =∠MAF ，∴△MEB ≌△MF A （AAS ） ∴BE =AF .∵D 是AB 的中点，即BD =AD ， 又∵∠DBE =∠DAF ，∴△DBE ≌△DAF （SAS ） ∴DE =DF .图1M F E DCB A（3）DE=DF.如图，作AM的中点G，BM的中点H，连DG，FG，DH，EH.∵点D是边AB的中点，∴DG∥BM，DG=12BM.同理可得：DH∥AM，DH=12AM.∵ME⊥BC于E，H是BM的中点.∴在Rt△BEM中，HE=12BM=BH.∴∠HBE=∠HEB.∴∠MHE=2∠HBE.又∵DG=12BM，HE=12BM，∴DG=HE.同理可得：DH=FG. ∠MGF=2∠MAC.∵DG∥BM，DH∥GM，∴四边形DHMG是平行四边形.∴∠DGM=∠DHM.∵∠MGF=2∠MAC，∠MHE=2∠MBC，∠MBC=∠MAC，∴∠MGF=∠MHE.∴∠DGM+∠MGF=∠DHM+∠MHE.∴∠DGF=∠DHE.在△DHE与△FGD中DG HEDGF DHEDH FG=⎧⎪∠=∠⎨⎪=⎩∴△DHE≌△FGD（SAS）∴DE=DF.图2AB CD FM高中数学知识点二次函数（1）一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ，且12x x ≤．令2()f x ax bx c =++，从以下四个方面来分析此类问题：①开口方向：a ②对称轴位置：2bx a=-③判别式：∆ ④端点函数值符号． ①k ＜x 1≤x 2 ⇔②x 1≤x 2＜k ⇔③x 1＜k ＜x 2 ⇔ af (k )＜0④k 1＜x 1≤x 2＜k 2 ⇔⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+． （Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q =②02b x a->，则()M f p = xxx(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．x>O-=f (p) f (q)()2bf a-g0x x>O-=f(p) f(q)()2b f a-0x gx<O-=f (p) f (q) ()2bf a-x<O-=f (p)f(q)()2b f a-x<O-=f (p)f(q)()2bf a-x gx<O-=f (p)f (q)()2b f a-x<O-=f (p)f (q)()2b f a-gx。

中点模型的构造及应用一、遇到以下情况考虑中点模型：任意三角形或四边形中点或与中点有关的线段出现两个或三个中点考虑三角形中线定理已知直角三角形斜边中点，可以考虑构造斜边中线已知等边、等腰三角形底边中点，可以考虑与顶角连接用“三线合一”有些题目不直接给出中点，我们可以挖掘其中隐含中点，比如等腰三角形、等边三角形、直角三角形、平行四边形、圆中圆心是直径中点等可以出现中点的图形通常考虑用中点模型三角形中线的交点称为重心，它把中线分的线段比为2:1二、中点模型辅助线构造方法分类（一）倍长中线法（构造全等三角形，八字全等）当已知条件中出现中线时，常常将此中线倍长构造全等三角形解决问题。

如图，在∆ABC中，D为BC中点，延长AD到E使AD=DE，连接BE，则有：∆ADC≌∆EDB。

作用：转移线段和角。

（二）倍长类中线法（与中点有关线段，构造全等三角形，八字全等）当已知条件中出现类中线时，常常将此类中线倍长构造全等三角形解决问题。

如图，在∆ABC中，D为BC中点，延长ED到F使ED=DF，连接CF，则有：∆BED≌∆CFD。

作用：转移线段和角。

（三）直角三角形斜边中线法当已知条件中同时出现直角三角形和中点时，常构造直角三角形斜边中线，然后再利用直角三角形斜边的中线性质解决问题。

如下图，在Rt ∆ABC 中，A C B 90∠=︒，D 为AB 中点，则有：12CD AD BD AB ===（四）等腰三角形三线合一当出现等腰三角形时，常隐含有底边中点，将其与顶角连接，可构成三线合一。

在∆中:（1）AC=；（2）CD 平分ACB ∠；（3）AD=，（4）CD AB ⊥ “知二得二”：比如由（2）（3）可得出（1）（4）.也就是说，以上四条语句，任意选择两个作为条件，就可以推出剩下两条。

（五）中位线法当已知条件中同时出现两个及以上中点时，常考虑构造中位线；或出现一个中点，要求证明平行线段或线段倍分关系时也常考虑构造中位线。

初中数学中点模型归纳总结中点模型是初中数学中一个重要的概念，常用于几何图形的证明和计算中。

通过对中点模型的归纳总结，可以更好地理解和运用这一概念。

本文将分别从数轴中点、线段中点和三角形中点三个方面进行归纳总结。

一、数轴中点数轴中点是指数轴上离两个点距离相等的点。

在数轴上，如果A、B两个点的坐标分别为a和b，那么它们的中点的坐标可以通过以下公式计算：中点坐标 = (a + b) / 2通过这个公式，我们可以很方便地求解两个点的中点坐标。

同时，我们还可以推广到三个点的情况：三点中点坐标 = (a + b + c) / 3这个公式也可以以类似的方式计算。

二、线段中点线段中点是指线段上距离两个端点相等的点。

在线段AB上，如果A、B两个点的坐标分别为（x1，y1）和（x2，y2），那么它们的中点的坐标可以通过以下公式计算：中点坐标 = ((x1 + x2) / 2, (y1 + y2) / 2)通过这个公式，我们可以计算出线段AB的中点坐标。

同样地，我们还可以推广到三维空间中的情况：三维空间中点坐标 = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3, (z1 + z2 +z3) / 3)这个公式在三维几何场景中也能帮助我们求解线段的中点坐标。

三、三角形中点三角形中点是指连接三角形三个顶点与对边中点的线段所构成的三个线段的交点。

三角形的三个中点分别是三边中点、三角形重心和三角形外心。

下面我们分别来介绍它们的特点和计算方法。

1. 三边中点：连接三角形三个顶点与对边中点的线段的交点，分别记为M1、M2、M3。

这三个点构成的线段M1M2、M2M3和M3M1分别平分三角形的三条边，且交于三角形的重心G。

2. 三角形重心：三角形重心是连接三角形三个顶点与对边中点的线段的交点，记为G。

三角形的重心是三条中线的交点，其中中线是连接三角形的一个顶点与对边中点的线段。

3. 三角形外心：三角形外心是三角形三边垂直平分线的交点，记为O。