下载文档原格式
计算机辅助几何造型技术主讲教师：秦开怀教授、博导qkh-dcs@所在单位：清华大学计算机科学与技术系 时间：2007年9月~2008年1月Textbooks/ReferencesJ. Hoschek& D. Lasser, Fundamentals of Computer Aided Geometric Design A K Peters Computer Aided Geometric Design, A K Peters, Ltd, Massachusetts, 1993.David F Rogers Introduction to NURBS Morgan David F Rogers,Introduction to NURBS, Morgan Kaufmann,2001.L Piegl&W Tiller The NURBS Book(2L. Piegl & W. Tiller, The NURBS Book (2nd Edition), Springer-Verlag Berlin Heidelberg, NewYork, 1997.York1997Carl deBoor, A Practical Guide to Splines, New York, Springer Verlag, 1978.York Springer-Verlag1978(Continued)M. E. Mortenson, Geometric Modeling , J h W l &S I 1985John Waley & Sons, Inc., 1985. G. Farin, Curves and Surfaces for ,Computer Aided Geometric Design (5th Edition), Elsevier Inc., 2002.(李双喜译，),,(CAGD 曲线曲面，科学出版社，2006）E J Stollnitz T DeRose &D H Salesin E. J. Stollnitz, T. DeRose & D. H. Salesin, Wavelets for Computer Graphics, Theory & Morgan Kaufmann PublishersApplications , Morgan Kaufmann Publishers, Inc., San Francisco, 1996.(Continued)Denis Zorin & Peter Schroder, Subdivision for M d li d A i ti SIGGRAPH 2000Modeling and Animation , SIGGRAPH 2000 Course Notes #23, 2000. R. Barzel, Physically-Based Modeling for Computer Graphics, A Structured Approach,Academic Press, Inc., San Diego, 1992.D. N. Metaxas, Physic-Based Deformable ,yModels, Applications to Computer Vision, Graphics & Medical Imaging , Kluwer Academicp g g ,Publishers, Massachusetts, 1997.(Continued)Donald Hearn & M.Pauline Baker, C t G hi ith O GL (Thi d Computer Graphics with OpenGL (Third Edition), Pearson Education, 2004 (中译本赫恩等著本：赫恩等著, 蔡士杰等译,《计算机图形学（第三版）》, 电子工业出版社, 200506)2005-06.) J. D. Foley, et al, Computer Graphics: y,,p pPrinciples & Practice (2nd Edition in C),Addison-Wesley, Reading, MA, 1996.y,g,,G di P li Grading PolicyThree assignments 30%Discussions/learning in classroom 5% One project substituting for the final p j g examination 65%R kRemarksThe three assignment is to be completed individually on yourself, but discussions among fellow students areyourself but discussions among fellow students areallowed.The project substitutes for the final examination Two The project substitutes for the final examination. Twostudents can work together as a group.Absolutely no sharing or copying of any code for both Absolutely no sharing or copying of any code for boththe assignments and the project! Offenders will be givena failure grade and the case will be reported to theg pdepartment.You are welcome to turn off your mobile phone before You are welcome to turn off your mobile phone beforeattending lectures.This course concentrates on seven main issues:i iNURBS curves and surfaces (including Bezier, B-spline curves and surfaces)gTriangular surfacesGordon-Coons surfacesSubdivision surfaces of arbitrary topologySubdivision surfaces of arbitrary topologyThe 2nd generation wavelets for multi-resolution modelingmodelingSolid modelingNew technology for geometric modelingContents of This Course1.Introduction2.∆Mathematic BasicsAffine mapsAffine mapsDivided differenceFunction spaceGeometric basics from curves and surfaces 3.∆Interpolatory Polynomial SplinesHermite interpolationHermite interpolationContents of This Course Contents of This Course (Continued)Quadric polynomial spline curvesCubic polynomial spline curvesSolving a linear system of equations with a g y q tridiagonal coefficient matrix Cubic parametric spline curves Cubic parametric spline curves4.*Bezier Curves and Surfaces Bezier curves defined by edge vectorsBernstein-Bezier curvesProperties of Bernstein-Bezier curves(Continued)De Casteljau algorithmDi t ti f B iDiscrete generation of Bezier curvesDegree elevation of Bezier curvesD d i f B iDegree reduction of Bezier curvesBezier spline curvesBezier interpolation curvesMatrix formula of Bezier curvesRational Bezier curvesProduct & inner product of Bezier curves Bezier surfaces(Continued)5.*B-spline Curves and SurfacesB-spline basis functions and their p ppropertiesB-spline curvesOpen curves and knot vectorsOpen curves and knot vectorsUniform B-spline curvesEndpoint interpolating B spline curves Endpoint interpolating B-spline curvesClosed B-spline curves(Continued)Chaikin algorithmDe Boor algorithmInserting knots in B-spline curves Inserting knots in B spline curvesBoehm algorithmOlso algorithmGeneral knot insertion for B-spline curvesDegree elevation of B-spline curves Degree elevation of B-spline curvesMarsden identity and recursive degree elevationPrautzsch algorithm(Continued)Arbitrarily high degree elevation for B-spline curvesDegree reduction of B-spline curvesB-spline surfacesInterpolating B-spline curves and p g p surfaces Matrix formulas of B-spline curves and Matrix formulas of B spline curves and surfaces(Continued)Matrix formula of uniform B_spline curvesMatrix formula of non-uniform B_splines Inner product of B-spline curvesGeneralized Marsden identityB-spline curve productInner product of B-spline basis functionsInner product of B-spline curves6.*NURBS Curves and SurfacesNURBS curvesNURBS curvesRepresenting conics using NURBS(Continued)Parameterization of curvesfNURBS surfacesRepresenting quadrics using NURBS surfacesfInterpolating NURBS curves and surfaces 7.Blossoming PrincipleLooking at de Casteljau algorithm from a Looking at de Casteljau algorithm from a blossoming point of viewKnot insertion from a blossoming point of Knot insertion from a blossoming point of view(Continued)Generating de Boor points based on the blossoming principleblossoming principleDegree raising of B-spline curves by blossoming8.* Triangular SurfacesBarycentric coordinatesgTriangular Bezier surfacesContinuity conditions for triangular Bezier ppatchesRational Triangular surfaces(Continued)9.*Gordon-Coons SurfacesCoons surfacesGordon-Coons surfaces on rectanglesGordon-Coons surfaces on triangles0Subd s o Su a s o b a y 10.*Subdivision Surfaces of ArbitraryTopologyCatmull-Clark surfacesCatmull-Clark surfacesDoo-Sabin surfacesContinuity of uniform subdivision surfaces Continuity of uniform subdivision surfacesNon-uniform subdivision surfaces(Continued)Convergence and continuity of non-uniform subdivision surfaces11.*The 2nd Generation Wavelets forMulti-resolution modelingMulti-resolution modelingB-spline wavelets for Multi-resolution modeling Endpoint interpolating B-spline wavelets Endpoint interpolating B-spline waveletsArbitrary Non-uniform B-spline waveletsB-spline wavelets with constraintsB spline wavelets with constraintsSubdivision-based Surface waveletsLoop Subdivision WaveletsCatmull-Clark Subdivision Wavelets√3-subdivision-based Bi-orthogonal Wavelets(Continued)12.∆Scattered Data Interpolation13.*Intersections of Curves and Surfaces14.Solid Modeling14*Solid Modeling15.Parameterization Modeling for ShapeDesign and Feature-based Modeling 16.New Technology for Geometric 16.*New Technology for GeometricModelingHierarchical B splinesHierarchical B-splinesPhysics-based modelingContents of This Course Contents of This Course (Continued)Modeling fractalized scenes (mountains,f lowers etc.)Particle system for modeling fires, clouds, water, forests etc.1.Introduction1. IntroductionSome Applications of CAGDRepresentation of large data setsVisualizing productsAutomatically producing sectionalAutomatically producing sectional drawingsModeling surfaces arising inModeling surfaces arising in construction of cars, ships & airplanesDesigning pipe systems, e.g. in chemical plants(continued)Drawing marine charts and city and relief i h maps in cartographyProduction and quality control, e.g. in q y ,g the sewing machine, textile and shoe industriesPlanning and controlling surgery Creating images in advertising television Creating images in advertising, television and film industries(continued)Constructing virtual environmentsDescribing robot paths and controlling their movementstheir movementsControlling milling machines used in manufacturingCurve modeling with constrained B-spline wavelets 保特征点的多分辨率曲线造型29曲线的多分辨率分段无缝表示30细分曲面带约束的样条曲面小波左图是采用经典B 样条曲面小波分片多分辨率表示的结果,右图是采用带约束B 的样条曲面小波分片多分辨率表示的结果,其中约束施加在接合线处。
计算机辅助几何设计专业介绍计算机辅助几何设计（Computer Aided Geometric Design,简写为CAGD）主要研究曲面造型的数学基础理论与方法。
1974年在美国的Utah大学举行了名为CAGD的学术会议，这次会议标志着CAGD作为计算数学的一个分支学科正式建立。
上世纪八十年代初，中国科学技术大学数学系的常庚哲教授和冯玉瑜教授分别在美国Utah大学、Brown大学和Wisconsin大学系统学习CAGD、样条函数和函数逼近论等最新进展。
随后两人相继回到中国科大，于1982年招收了第一批硕士研究生。
他们的归国与合作，标志着数学系CAGD研究小组的正式建立。
初期，CAGD研究小组在曲面的保形与逼近、三角域上的Bernstein-Bézier 曲面、样条函数等方面取得了一系列令国内外同行所关注的成果，曾获得中科院自然科技成果二等奖。
常庚哲教授于1984年到2000年一直担任国际刊物《Computer Aided Geometric Design》的编委，并于2007年在第三届全国几何设计与计算学术会议上获得由中国工业与应用数学学会几何设计与计算专业委员会颁发的首届“中国几何设计与计算贡献奖”。
研究小组与美国和欧洲等地的学者建立了广泛的国际联系。
近十年来，随着常庚哲教授和冯玉瑜教授相继退休，本研究小组队伍大大年轻化，形成了以陈发来、邓建松教授为主的年轻学术梯队，其中陈发来教授2002年获得国家杰出青年基金，并担任国际著名期刊《The Visual Computer》以及多个国内期刊的编委，多次担任国际会议的程序委员。
本小组继承了常庚哲、冯玉瑜教授开创的传统，在以计算代数几何为工具进行几何造型方面做了有特色的工作。
近几年来在以下几方面做了较为系统的研究：（1）分片代数曲面造型：通过系统学习计算代数几何的理论，提出了各种应用计算代数几何理论构造分片代数曲面的算法框架。
最近又基于优化的理论，提出了隐式曲面重构的新型算法，解决了以往方法中剖分难以构造等困难。
《计算机辅助技术》考试大纲一、考试内容《计算机辅助技术》是面向机械工程、工业工程和航空宇航制造工程专业的技术基础课。
根据本课程是计算机辅助技术普及性教学的特点，对考试范围作以下要求：1.设计制造过程中的计算机辅助技术：包括设计与制造过程的产品循环；计算机辅助技术在设计制造过程中的作用；计算机辅助技术的特点和应用发展历史。
2.计算机辅助技术应用系统软硬件构成：包括系统软硬件典型配置、输入输出设备以及软件系统的构成。
3.计算机图形学概述：包括2维、3维图形显示的算法和处理过程；真实感图形的显示和应用；用户界面设计。
4.计算机辅助几何造型设计概述：包括几何模型的作用、分类；线架、曲面和实体造型方法的基本特点。
5.计算机辅助工程（CAE）：包括有限元分析方法的原理与基本过程。
6.计算机辅助制造技术（CAM）：主要讲解数控机床与机器人的应用方法。
包括数控机床的组成、分类、与功能；手工数控编程、自动编程的基本过程；DNC与CNC技术的组成与特点；机器人的组成、编程与应用。
7.计算机辅助工艺过程设计（CAPP）：包括成组技术的原理及应用， CAPP的基本组成、分类；CAPP工艺决策的原理。
8.计算机辅助测试技术（CAT）：包括数控测量机构成，数控测量的常用方法。
9.计算机集成制造系统（CIMS）：CIMS的概念，CIMS的组成；柔性制造系统（FMS）、并行工程、敏捷制造等先进制造技术的基本概念。
二、参考书目1.何卫平主编，计算机辅助技术基础，西北工业大学出版社，1998CAD-computer aided design计算机辅助设计CAM- computer aided manufacturing计算机辅助制造CAPP- computer aided process plan计算机辅助工艺过程设计CAE- computer aided engineering计算机辅助工程CA T- computer aided test计算机辅助测试MIS-制造管理信息系统MRPII-物料资源规划ERP-企业资源规划PDM-产品数据管理CIMS-计算机集成制造系统MES-制造执行管理系统BPR-业务进程组构1.应用生产过程、生产环节中的辅助技术：2.硬件设备：3.图形计算和阴暗处理：LED：low emitting diode发光二极管，CRT：cathode-ray tube阴极射线管4.CAGD-computer aided geometry design的三种几何模型：①线架模型，是表面模型与实体模型的基础，它用空间线条构成物体，其表达形式是顶点与棱边，顶点与棱边确定，物体就被唯一确定；②表面模型，用一组表面表示物体的外形，将棱边有序地连接而构成实体的表面结构；③实体模型，用基本体素构造物体。
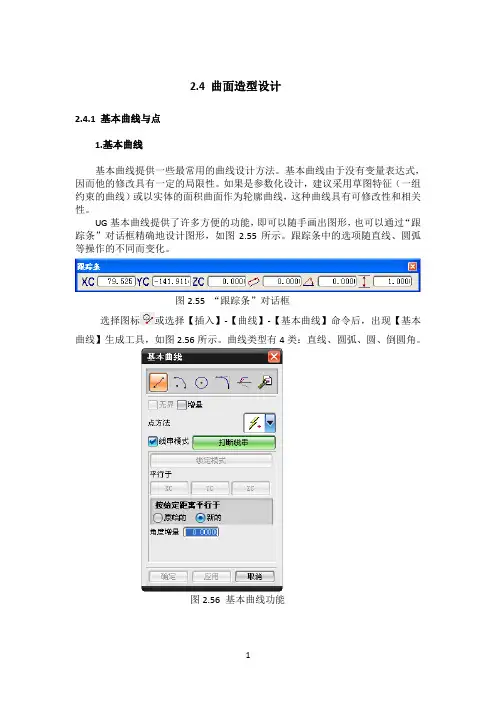
2.4 曲面造型设计2.4.1 基本曲线与点1.基本曲线基本曲线提供一些最常用的曲线设计方法。
基本曲线由于没有变量表达式，因而他的修改具有一定的局限性。
如果是参数化设计，建议采用草图特征（一组约束的曲线）或以实体的面积曲面作为轮廓曲线，这种曲线具有可修改性和相关性。
UG基本曲线提供了许多方便的功能，即可以随手画出图形，也可以通过“跟踪条”对话框精确地设计图形，如图2.55所示。
跟踪条中的选项随直线、圆弧等操作的不同而变化。
图2.55 “跟踪条”对话框选择图标或选择【插入】-【曲线】-【基本曲线】命令后，出现【基本曲线】生成工具，如图2.56所示。
曲线类型有4类：直线、圆弧、圆、倒圆角。
图2.56 基本曲线功能2. 点和点集1）点利用点构造器每次可生成一个点，并且作为一个独立的几何对象，以+标识。
2）点集点集一次可以生成一组点，这些点从已存在的曲线（或曲面）上获得。
图2.57所示为成成点集方法的对话框。
图2.57 点集生成方法对话框2.4.2 样条曲线曲线的表示分为两大类：计算类曲线和构造类曲线。
（1）计算类曲线：直接有数学表达式定义的曲线，如直线、二次曲线、求交曲线、投影曲线、偏置曲线，其中除了直线与二次曲线外，其他曲线都是在已有曲线的基础上计算得到的曲线。
（2）构造类曲线：由点或参数定义的曲线，如样条曲线、螺旋线、规律曲线，用户必须输入一系列点或参数，通过插值、逼近、拟合方法来构造这些曲线。
1. 样条曲线的基本概念样条曲线在工程设计中有着广泛的应用。
在飞机、汽车、船舶等具有大量曲面的工程设计中，基本的曲线构造方法已不能满足设计要求，需要一种能够表达非解析函数形式的曲线或曲面定义，这类曲线被称为自由曲线（自由曲线是一种由逼近、拟合或插值方法得到的曲线），用户对区县的相撞控制有非常大的灵活性。
而且，许多曲面也是利用曲线经过不同的操作生成的，例如放样面、直纹面、网格面、扫掠面等都是以自由曲线作为输入数据的。
《计算机辅助造型与自动编程应用》课程标准一、课程性质与作用课程的性质：《计算机辅助造型与自动编程应用》课程是数控技术专业的专业核心课程，重点是通过计算机辅助设计与计算机辅助制造实现产品快速设计与虚拟制造的基础。
通过本课的学习，要求学生熟练应用Pro/E软件实现机械产品的造型设计任务；能熟练应用CAXA数控车软件，掌握各种典型车削类零件的造型方法及自动编程技术；能熟练应用CAXA制造工程师软件，掌握各种铣削类典型零件的造型方法及自动编程方法等。
课程的作用：本课程在专业人才培养过程中起到核心作用。
学完本课程，能够达到“熟练应用常用的CAD/CAM软件进行计算机辅助造型和自动编程的能力，为后续的毕业设计和走向工作岗位奠定坚实的基础。
二、课程的教育目标通过本课程的学习，能够达到人才培养模式中的知识目标、素质目标、能力目标。
（一）知识目标（1）通过使用用三维CAD软件进行二维草图绘制和三维零件造型，掌握典型产品零件的三维模型造型及曲面造型的方法与技巧。
（2）通过使用三维CAD软件完成三维零件的装配，并掌握零件装配的方法与技巧。
（3）能按机械零部件的结构设计和绘制标准要求生成工程图。
（4）能过熟练使用CAM软件进行车削类零件造型和数控加工自动编程。
（5）能过熟练使用CAM软件进行铣削类零件三维造型和数控加工自动编程。
（二）素质目标（1）培养学生独立思考灵活运用所学知识解决实际问题的应用能力（2）培养学生勇于创新、敬业爱业的工作作风（3）培养学生的与人沟通能力及团队协作精神（4）培养学生的质量意识、安全意识、环保意识（5）培养学生踏实务实的工作习惯（6）培养学生的社会责任心（三）能力目标（1）具备正确分析零件结构，能根据图纸要求，运用所学知识快速完成零件造型的能力。
（2）具备正确分析部件中各零件的装配关系，能够按照要求，运用所学知识快速完成零部件装配的能力。
（3）具备能按够按照绘图标准和要求生成工程图的能力。
