下载文档原格式
实际问题与一元一次方程（一）基础【学习目标】1.熟练掌握分析解决实际问题的一般方法及步骤；2.熟悉行程，工程，配套及和差倍分问题的解题思路．【要点梳理】知识点一、用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题−−−→分析抽象方程−−−→求解检验解答．由此可得解决此类 题的一般步骤为：审、找、设、列、解、检、答．要点诠释：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系。
（2）“找”寻找等量关系；（3）“设”就是设未知数，一般求什么就设什么为x ，但有时也可以间接设未知数；（4）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一；（5）“解”就是解方程，求出未知数的值．（6）“检”就是指检验方程的解是否符合实际意义，当有不符合的解时，及时指出，舍去即可；（7）“答”就是写出答案，注意单位要写清楚． 知识点二、常见列方程解应用题的几种类型1．和、差、倍、分问题（1）基本量及关系：增长量＝原有量×增长率，现有量＝原有量+增长量，现有量＝原有量-降低量．（2）寻找相等关系：抓住关键词列方程，常见的关键词有：多、少、和、差、不足、剩余以及倍，增长率等．2．行程问题（1）三个基本量间的关系： 路程=速度×时间（2）基本类型有：①相遇问题（或相向问题）：Ⅰ．基本量及关系：相遇路程=速度和×相遇时间Ⅱ．寻找相等关系：甲走的路程+乙走的路程＝两地距离． ②追及问题：Ⅰ．基本量及关系：追及路程=速度差×追及时间Ⅱ．寻找相等关系：第一， 同地不同时出发：前者走的路程＝追者走的路程；第二， 同时不同地出发：前者走的路程+两者相距距离＝追者走的路程．③航行问题：Ⅰ．基本量及关系：顺流速度=静水速度+水流速度，逆流速度=静水速度－水流速度，顺水速度－逆水速度＝2×水流速度；Ⅱ．寻找相等关系：抓住两地之间距离不变、水流速度不变、船在静水中的速度不变来考虑．3．工程问题如果题目没有明确指明总工作量，一般把总工作量设为1．基本关系式：（1）总工作量=工作效率×工作时间；（2）总工作量=各单位工作量之和．4．调配问题寻找相等关系的方法：抓住调配后甲处的数量与乙处的数量间的关系去考虑．【典型例题】类型一、和差倍分问题1．2011年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米，其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米，问生产运营用水和居民家庭用水各多少亿立方米?【答案与解析】设生产运营用水x 亿立方米，则居民家庭用水(5.8-x )亿立方米．依题意，得5.8-x ＝3x+0.6解得x ＝1.35.8-x ＝5.8-1.3＝4.5（亿立方米）答：生产运营用水1.3亿立方米，居民家庭用水4.5亿立方米．【总结升华】本题要求两个未知数，不妨设其中一个未知数为x ，另外一个用含x 的式子表示．本题的相等关系是生产运营用水量+居民家庭用水总量＝5.8亿立方米．举一反三：【变式】(麻城期末考试)麻商集团三个季度共销售冰箱2800台，第一个季度销售量是第二个季度的2倍．第三个季度销售量是第一个季度的2倍，试问麻商集团第二个季度销售冰箱多少台?【答案】解：设第二个季度麻商集团销售冰箱x 台，则第一季度销售量为2x 台，第三季度销售量为4x 台，依题意可得：x+2x+4x ＝2800，解得：x ＝400答：麻商集团第二个季度销售冰箱400台．类型二、行程问题1.一般问题2．小山娃要到城里参加运动会，如果每小时走4千米，那么走完预订时间离县城还有0.5千米，如果他每小时走5千米，那么比预订时间早半小时就可到达县城．试问学校到县城的距离是多少千米?【答案与解析】解：设小山娃预订的时间为x 小时，由题意得：4x+0.5＝5(x -0.5)，解得x ＝3．所以4x+0.5＝4×3+0.5＝12.5(千米)．答：学校到县城的距离是12.5千米．【总结升华】当直接设未知数有困难时，可采用间接设的方法．即所设的不是最后所求的，而是通过求其它的数量间接地求最后的未知量．举一反三：【变式】某汽车在一段坡路上往返行驶，上坡的速度为10千米/时，下坡的速度为20千米/时，求汽车的平均速度．【答案】解：设这段坡路长为a 千米，汽车的平均速度为x 千米/时，则上坡行驶的时间为10a 小时，下坡行驶的时间为20a 小时．依题意，得：21020a a x a ⎛⎫+= ⎪⎝⎭， 化简得： 340ax a =．显然a ≠0，解得1133x =答：汽车的平均速度为1133千米/时． 2.相遇问题（相向问题）【高清课堂：实际问题与一元一次方程(一) 388410 相遇问题】3． A 、B 两地相距100km ，甲、乙两人骑自行车分别从A 、B 两地出发相向而行，甲的速度是23km/h ，乙的速度是21km/h ，甲骑了1h 后，乙从B 地出发，问甲经过多少时间与乙相遇？【答案与解析】解:设甲经过x 小时与乙相遇.由题意得：()2312321(1)100x ⨯++-= 解得，x=2.75答：甲经过2.75小时与乙相遇．【总结升华】等量关系：甲走的路程+乙走的路程=100km举一反三：【变式】甲、乙两人骑自行车，同时从相距45km 的两地相向而行，2小时相遇，每小时甲比乙多走2.5km ，求甲、乙每小时各行驶多少千米?【答案】解：设乙每小时行驶x 千米，则甲每小时行驶(x +2.5)千米，根据题意，得：2( 2.5)245x x ++=解得：10x =2.510 2.512.5x +=+=（千米）答：甲每小时行驶12.5千米，乙每小时行驶10千米3.追及问题（同向问题）4．一队学生去校外进行军事野营训练，他们以5千米/时的速度行进，走了18分钟时，学校要将一紧急通知传给队长，通讯员从学校出发，骑自行车以14千米/时的速度按原路追上去，通讯员用多少分钟可以追上学生队伍?【答案与解析】解：设通讯员x 小时可以追上学生队伍，则根据题意，得18145560x x =⨯+， 得：16x =， 16小时=10分钟． 答：通讯员用10分钟可以追上学生队伍．【总结升华】追及问题：路程差=速度差×时间，此外注意：方程中x 表示小时，18表示分钟，两边单位不一致，应先统一单位．4.航行问题（顺逆风问题）5．一艘船航行于A 、B 两个码头之间，轮船顺水航行需3小时，逆水航行需5小时，已知水流速度是4千米/时，求这两个码头之间的距离．【答案与解析】解法1：设船在静水中速度为x 千米/时，则船顺水航行的速度为(x+4)千米/时，逆水航行的速度为(x -4)千米/时，由两码头的距离不变得方程：3(x+4)＝5(x -4)，解得：x=16，（16+4）×3=60（千米）答：两码头之间的距离为60千米．解法2：设A 、B 两码头之间的距离为x 千米，则船顺水航行时速度为3x 千米/时，逆水航行时速度为5x 千米/时，由船在静水中的速度不变得方程：4435x x -=+，解得：60x = 答：两码头之间的距离为60千米．【总结升华】顺流速度=静水速度+水流速度；逆流速度=静水速度-水流速度，根据两个码头的距离不变或船在静水中的速度不变列方程．类型三、工程问题6．一个水池有两个注水管，两个水管同时注水，10小时可以注满水池；甲管单独开15小时可以注满水池，现两管同时注水7小时，关掉甲管，单独开乙管注水，还需要几小时能注满水池? 【思路点拨】视水池的蓄水量为“1”，设乙管还需x 小时可以注满水池；那么甲乙合注1小时注水池的110，甲管单独注水每小时注水池的115，合注7小时注水池的710，乙管每小时注水池的111015⎛⎫- ⎪⎝⎭． 【答案与解析】解：设乙管还需x 小时才能注满水池．由题意得方程：1171101510x ⎛⎫-=- ⎪⎝⎭解此方程得：x ＝9答：单独开乙管，还需9小时可以注满水池．【总结升华】工作效率×工作时间=工作量，如果没有具体的工作量，一般视总的工作量为“1” ． 举一反三：【变式】修建某处住宅区的自来水管道，甲单独完成需14天，乙单独完成需18天，丙单独完成需12天，前7天由甲、乙两人合作，但乙中途离开了一段时间，后两天由乙、丙合作完成问乙中途离开了几天?【答案】解：设乙中途离开x 天，由题意得1117(72)21141812x ⨯+-++⨯= 解得：3x =答：乙中途离开了3天类型四、调配问题（比例问题、劳动力调配问题）7．星光服装厂接受生产某种型号的学生服的任务，已知每3m 长的某种布料可做上衣2件或裤子3条，一件上衣和一条裤子为一套，计划用750m 长的这种布料生产学生服，应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?【思路点拨】每3米布料可做上衣2件或裤子3条，意思是每1米布料可做上衣32 件，或做裤子1条，此外恰好配套说明裤子的数量应该等于上衣的数量．【答案与解析】解：设做上衣需要xm ，则做裤子为(750-x )m ，做上衣的件数为23x ⨯件，做裤子的件数为75033x -⨯，则有：23(750)33x x -= 解得：x ＝450， 750-x ＝750-450＝300(m )，45023003⨯=（套） 答：用450m 做上衣，300m 做裤子恰好配套，共能生产300套．【总结升华】用参数表示上衣总件数与裤子的总件数，等量关系：上衣总件数＝裤子的总件数． 举一反三：【高清课堂：实际问题与一元一次方程(一) 调配问题】【变式】甲队有72人，乙队有68人，需要从甲队调出多少人到乙队，才能使甲队恰好是乙队人数的34. 解：设从甲队调出x 人到乙队.由题意得， ()372684x x -=+ 解得，x=12. 答：需要从甲队调出 12人到乙队，才能使甲队恰好是乙队人数的34 .实际问题与一元一次方程（二）（提高）【学习目标】1.熟练掌握分析解决实际问题的一般方法及步骤；2.熟悉行程，工程，配套及和差倍分问题的解题思路．【要点梳理】要点一、用一元一次方程解决实际问题的一般步骤要点二、常见列方程解应用题的几种类型（待续）1．和、差、倍、分问题（1）基本量及关系：增长量＝原有量×增长率，现有量＝原有量+增长量，现有量＝原有量-降低量．（2）寻找相等关系：抓住关键词列方程，常见的关键词有：多、少、和、差、不足、剩余以及倍，增长率等．2．行程问题（1）三个基本量间的关系： 路程=速度×时间（2）基本类型有：①相遇问题（或相向问题）：Ⅰ．基本量及关系：相遇路程=速度和×相遇时间Ⅱ．寻找相等关系：甲走的路程+乙走的路程＝两地距离．②追及问题：Ⅰ．基本量及关系：追及路程=速度差×追及时间Ⅱ．寻找相等关系：第一，同地不同时出发：前者走的路程＝追者走的路程；第二，同时不同地出发：前者走的路程+两者相距距离＝追者走的路程．③航行问题：Ⅰ．基本量及关系：顺流速度=静水速度+水流速度，逆流速度=静水速度－水流速度，顺水速度－逆水速度＝2×水速；Ⅱ．寻找相等关系：抓住两地之间距离不变、水流速度不变、船在静水中的速度不变来考虑．3．工程问题如果题目没有明确指明总工作量，一般把总工作量设为1．基本关系式：（1）总工作量=工作效率×工作时间；（2）总工作量=各单位工作量之和．4．调配问题寻找相等关系的方法：抓住调配后甲处的数量与乙处的数量间的关系去考虑．【典型例题】类型一、和差倍分问题1．旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%，第二次旅程中用去剩余汽油的40%，这样油箱中剩的汽油比两次所用的汽油少1公斤，求油箱里原有汽油多少公斤？【答案与解析】解：设油箱里原有汽油x 公斤，由题意得：x(1-25%)(1-40%)+1=25%x+(1-25%)x×40%解得：x=10答：油箱里原有汽油10公斤.【点评】等量关系为：油箱中剩余汽油+1=用去的汽油.举一反三：【变式】某班举办了一次集邮展览，展出的邮票若平均每人3张则多24张，若平均每人4张则少26张，这个班有多少学生?一共展出了多少张邮票?【答案】解：设这个班有x 名学生，根据题意得：3x+24＝4x -26解得：x ＝50所以3x+24＝3×50+24＝174答：这个班有50名学生，一共展出了174张邮票．类型二、行程问题1.车过桥问题2. 某桥长1200m ，现有一列匀速行驶的火车从桥上通过，测得火车从上桥到完全过桥共用了50s ，而整个火车在桥上的时间是30s ，求火车的长度和速度．【思路点拨】正确理解火车“完全过桥”和“完全在桥上”的不同含义．【答案与解析】解：设火车车身长为xm ，根据题意，得： 120012005030x x +-=， 解得：x ＝300，所以12001200300305050x ++==． 答：火车的长度是300m ，车速是30m/s ．【点评】火车“完全过桥”和“完全在桥上”是两种不同的情况，借助线段图分析如下(注：A 点表示火车头)：(1)火车从上桥到完全过桥如图(1)所示，此时火车走的路程是桥长+车长．(2)火车完全在桥上如图(2)所示，此时火车走的路程是桥长－车长．由于火车是匀速行驶的，所以等量关系是火车从上桥到完全过桥的速度＝整个火车在桥上的速度．举一反三：【变式】某要塞有步兵692人，每4人一横排，各排相距1米向前行走，每分钟走86米，通过长86米的桥，从第一排上桥到排尾离桥需要几分钟？【答案】解：设从第一排上桥到排尾离桥需要x 分钟，列方程得： 6928611864x ⎛⎫=-⨯+ ⎪⎝⎭， 解得：x ＝3答：从第一排上桥到排尾离桥需要3分钟．2.相遇问题（相向问题）3．小李骑自行车从A 地到B 地，小明骑自行车从B 地到A 地，两人都匀速前进.已知两人在上午8时同时出发，到上午10时，两人还相距36千米，到中午12点，两人又相距36千米.求A 、B 两地间的路程.【答案与解析】解：设A 、B 两地间的路程为x 千米，由题意得：363624x x -+= 解得：x =108．答：A 、B 两地间的路程为108千米.【点评】根据“匀速前进”可知A 、B 的速度不变，进而A 、B 的速度和不变.利用速度和=小李和小明前进的路程和／时间可得方程．举一反三：【高清课堂：实际问题与一元一次方程(一)388410二次相遇问题】【变式】甲、乙两辆汽车分别从A 、B 两站同时开出，相向而行，途中相遇后继续沿原路线行驶，在分别到达对方车站后立即返回，两车第二次相遇时距A 站34km ，已知甲车的速度是70km/h ，乙车的速度是52km/h ，求A 、B 两站间的距离.【答案】解：设A 、B 两站间的距离为x km ，由题意得：234347052x x -+= 解得：x=122答： A 、B 两站间的距离为122km. 3.追及问题（同向问题）4．一辆卡车从甲地匀速开往乙地，出发2小时后，一辆轿车从甲地去追这辆卡车，轿车的速度比卡车的速度每小时快30千米，但轿车行驶一小时后突遇故障，修理15分钟后，又上路追这辆卡车，但速度减小了13，结果又用两小时才追上这辆卡车，求卡车的速度． 【答案与解析】 解：设卡车的速度为x 千米/时，由题意得：1122(30)(1)(30)243x x x x x x +++=++-⨯+⨯ 解得：x=24答：卡车的速度为24千米/时．【点评】采用“线示”分析法，画出示意图．利用轿车行驶的总路程等于卡车行驶的总路程来列方程，理清两车行驶的速度与时间．4.航行问题（顺逆风问题）5．盛夏，某校组织长江夜游，在流速为2.5千米/时的航段，从A 地上船，沿江而下至B 地，然后溯江而上到C 地下船，共乘船4小时．已知A 、C 两地相距10千米，船在静水中的速度为7.5千米/时，求A 、B 两地间的距离．【思路点拨】由于C 的位置不确定，要分类讨论：（1）C 地在A 、B 之间；（2）C 地在A 地上游．【答案与解析】解：设A 、B 两地间的距离为x 千米．(1)当C 地在A 、B 两地之间时，依题意得．1047.5 2.57.5 2.5x x -+=+- 解这个方程得：x ＝20(千米)(2)当C 地在A 地上游时，依题意得：1047.5 2.57.5 2.5x x ++=+- 解这个方程得：203x = 答：A 、B 两地间的距离为20千米或203千米． 【点评】这是航行问题，本题需分类讨论，采用“线示”分析法画出示意图(如下图所示)，然后利用“共乘”4小时构建方程求解．5.环形问题6．环城自行车赛，最快的人在开始48分钟后遇到最慢的人，已知最快的人的速度是最慢的人速度的3倍，环城一周是20千米，求两个人的速度.【答案与解析】解；设最慢的人速度为x 千米/时，则最快的人的速度为x 千米/时， 由题意得:x×-x×=20 解得：x=10答：最快的人的速度为35千米/时，最慢的人的速度为10千米/时.【点评】这是环形路上的追及问题，距离差为环城一周20千米.相等关系为：最快的人骑的路程 - 最慢人骑的路程=20千米.举一反三：【变式】两人沿着边长为90m 的正方形行走，按A →B →C →D →A …方向，甲从A 以65m/min 的速度，乙从B 以72m/min 的速度行走，如图所示，当乙第一次追上甲时，在正方形的哪一条边上?【答案】解：设乙追上甲用了x 分钟，则有：72x -65x ＝3×90 2707x =（分） 答：乙第一次追上甲时走了2707227777⨯≈(m ) 此时乙在AD 边上 类型三、工程问题7．一个蓄水池有甲、乙两个进水管和一个丙排水管，单独开甲管6小时可注满水池；单独开乙管8小时可注满水池，单独开丙管9小时可将满池水排空，若先将甲、乙管同时开放2小时，然后打开丙管，问打开丙管后几小时可注满水池?【答案与解析】解：设再过x 小时可把水注满．由题意得：11111()2()168689x +⨯++-= 解得：30421313x ==． 答：打开丙管后4213小时可把水放满． 【点评】相等关系：甲、乙开2h 的工作量+甲、乙、丙水管的工作量=1．举一反三： 【变式】收割一块水稻田，若每小时收割4亩，预计若干小时完成，收割23后，改用新式农机，工作效率提高到原来的112倍，因此比预计时间提早1小时完成，求这块水稻田的面积．【答案】解：设这块水稻田的面积为x 亩，由题意得： 21331144142x x x =++⨯ 解得：36x =．答：这块水稻田的面积为36亩．类型四、配套问题（比例问题、劳动力调配问题）8．某工程队每天安排120个工人修建水库，平均每天每个工人能挖土5 m 3或运土3 m 3，为了使挖出的土及时被运走，问：应如何安排挖土和运土的工人?【答案与解析】解：设安排x 人挖土，则运土的有(120-x )人，依题意得：5x ＝3(120-x )，解得x ＝45．120-45＝75(人)．答：应安排45人挖土，75人运土．【点评】用参数表示挖土数与运土数，等量关系：挖土与运土的总立方米数应相等．举一反三：【高清课堂：实际问题与一元一次方程(一) 配制问题】【变式】某商店选用A 、B 两种价格分别是每千克28元和每千克20元的糖果混合成杂拌糖果后出售，为使这种杂拌糖果的售价是每千克25元，要配制这种杂拌糖果100千克，问要用这两种糖果各多少千克？【答案】解：设要用A 种糖果x 千克，则B 种糖果用(100-x)千克.依题意，得：28x+20(100-x)=25×100解得：x=62.5.当x=62.5时，100-x=37.5.答：要用A 、B 两种糖果分别为62.5千克和37.5千克.实际问题与一元一次方程（三）（基础）【学习目标】(1)进一步提高分析实际问题中数量关系的能力，能熟练找出相等关系并列出方程；(2)熟悉利润，存贷款，数字及方案设计问题的解题思路．【要点梳理】要点一、用一元一次方程解决实际问题的一般步骤要点三、常见列方程解应用题的几种类型（续）1．利润问题（1）=100% 利润利润率进价(2) 标价＝成本(或进价)×(1＋利润率)(3) 实际售价＝标价×打折率(4) 利润＝售价－成本(或进价)＝成本×利润率注意：“商品利润＝售价－成本”中的右边为正时，是盈利；当右边为负时，就是亏损.打几折就是按标价的十分之几或百分之几十销售．2．存贷款问题（1）利息=本金×利率×期数（2）本息和（本利和）＝本金＋利息＝本金＋本金×利率×期数＝本金×(1＋利率×期数)（3）实得利息=利息-利息税（4）利息税=利息×利息税率（5）年利率＝月利率×12（6）月利率＝年利率×121 3.数字问题已知各数位上的数字，写出两位数，三位数等这类问题一般设间接未知数，例如：若一个两位数的个位数字为a ，十位数字为b ，则这个两位数可以表示为10b+a ． 4．方案问题选择设计方案的一般步骤：（1）运用一元一次方程解应用题的方法求解两种方案值相等的情况．（2）用特殊值试探法选择方案，取小于（或大于）一元一次方程解的值，比较两种方案的优劣性后下结论． 【典型例题】类型一、利润问题【高清课堂：实际问题与一元一次方程(二) 利润问题例2】1．以现价销售一件商品的利润率为30%，如果商家在现有的价格基础上先提价40%，后降价50%的方法进行销售，商家还能有利润吗？为什么？ 【答案与解析】解：设该商品的成本为a 元，则商品的现价为(1+30%)a 元，依题意其后来折扣的售价为(1+30%)a ·(1+40%)(1-50%)=0.91a .∵0.91a -a =-0.09a ,∴0.09aa-·100%=-9%. 答：商家不仅没有利润，而且亏损的利润率为9%.【总结升华】解答此类问题时，一定要弄清题意．分清售价、进价、数量、利润之间的关系很重要． 举一反三：【高清课堂：实际问题与一元一次方程(二)388413利润问题例3】【变式1】某个商品的进价是500元，把它提价40%后作为标价.如果商家要想保住12%的利润率搞促销活动，请你计算一下广告上可写出打几折？ 【答案】解：设该商品打x 折，依题意，则： 500(1+40%)·10x=500（1+12%）. x=10 1.121.4⨯=8. 答：该商品的广告上可写上打八折.【变式2】张新和李明相约到图书大厦去买书，请你根据他们的对话内容(如图所示)，求出李明上次所买书籍的原价．【答案】解：设李明上次购买书籍的原价为x元，由题意得：0.8x+20＝x-12，解这个方程得：x＝160．答：李明上次所买书籍的原价是160元．类型二、存贷款问题2．爸爸为小强存了一个五年期的教育储蓄，年利率为2.7％，五年后取出本息和为17025元，爸爸开始存入多少元.【答案与解析】解：设爸爸开始存入x元.根据题意，得x＋x×2.7％×5＝17025.解之，得x＝15000答：爸爸开始存入15000元.【总结升华】本息和＝本金＋利息，利息＝本金×利率×期数．类型三、数字问题3．一个三位数，十位上的数是百位上的数的2倍，百位、个位上的数的和比十位上的数大2，又个位、十位、百位上的数的和是14，求这个三位数.【答案与解析】解：设百位上的数为x，则十位上的数为2x，个位上的数为14-2x-x由题意得：x+14-2x-x=2x+2解得：x=3∴ x=3， 2x=6，14-2x-x=5答：这个三位数为365【总结升华】在数字问题中应注意：（1）求的是一个三位数，而不是三个数；（2）这类应用题，一般设间接未知数，切勿求出x就答；(3) 三位数字的表示方法是百位上的数字乘以100，10位上的数字乘以10，然后把所得的结果和个位数字相加．举一反三：【变式】一个两位数，个位上的数字比十位上的数字大4，这个两位数又是这两个数字的和的4倍，求这个两位数.【答案】x+），由题意得：解：设十位上的数字为x，则个位上的数字为（4++=++⨯x x x x10(4)[(4)]4x=解得：4∴⨯++=410(44)48答：这两位数是48.类型四、方案设计问题4．为鼓励学生参加体育锻炼．学校计划拿出不超过1600元的资金再购买一批篮球和排球．已知篮球和排球的单价比为3:2，单价和为80元．(1)篮球和排球的单价分别是多少元?(2)若要求购买的篮球和排球的总数量是36个，且购买的篮球数量不少于26个．请探究有哪几种购买方案?【答案与解析】解：(1)设篮球和排球的单价分别为3x元和2x元．依题意3x+2x＝80，解得x＝16即 3x＝48，2x＝32答：篮球和排球的单价分别为48元和32元．(由列表可知，共有三种购买方案：方案一：购买篮球26个，排球10个；方案二：购买篮球27个，排球9个；方案三：购买篮球28个，排球8个．【总结升华】本例设未知数的方法很独特，值得借鉴．采用列表的方法探索方案，值得学习．举一反三：【变式】(武昌区期末调考)某校组织10位教师和部分学生外出考察，全程票价为25元，对集体购票，客运公司有两种优惠方案可供选择：方案一：所有师生按票价的88%购票；方案二：前20人购全票，从第21人开始，每人按票价的80%购票．(1)若有30位学生参加考察，问选择哪种方案更省钱?(2)参加考察的学生人数是多少时，两种方案车费一样多?【答案】解：设有x位学生参加考察．按方案一购票费用为：25×88%(10+x)＝22x+220按方案二购票费用为：20×25+25×80%(x+10-20)＝20x+300(1)当x＝30时：22x+220＝660+220＝880(元)20x+300＝600+300＝900(元)答：当有30位学生参加考察，选择方案一更省钱．(2)设22x+220＝20x+300，解得：x＝40答：参加考察的学生人数为40人时，两种方案车费一样多．实际问题与一元一次方程（四）（提高）【学习目标】(1)进一步提高分析实际问题中数量关系的能力，能熟练找出相等关系并列出方程； (2)熟悉利润，存贷款，数字及方案设计问题的解题思路． 【要点梳理】要点一、用一元一次方程解决实际问题的一般步骤 要点三、常见列方程解应用题的几种类型（续） 1．利润问题 （1）=100% 利润利润率进价(2) 售价＝ (1＋利润率). 成本 (3) 售价＝标价×打折率(4) 利润＝售价－成本(或进价) 利润＝ 成本×利润率注意：“商品利润＝售价－成本”中的商品利润为正时，是盈利；当为商品利润负时，就是亏损.打几折就是按标价的十分之几或百分之几十销售． 2．存贷款问题（1）利息=本金×利率×期数（2）本息和（本利和）＝本金＋利息＝本金＋本金×利率×期数＝本金×(1＋利率×期数) （3）实得利息=利息-利息税 （4）利息税=利息×利息税率 （5）年利率＝月利率×12 （6）月利率＝年利率×1213.数字问题已知各数位上的数字，写出两位数，三位数等这类问题一般设间接未知数，例如：若一个两位数的个位数字为a ，十位数字为b ，则这个两位数可以表示为10b+a ． 4．方案问题选择设计方案的一般步骤：（1）运用一元一次方程解应用题的方法求解两种方案值相等的情况．（2）用特殊值试探法选择方案，取小于（或大于）一元一次方程解的值，比较两种方案的优劣性后下结论． 【典型例题】类型一、利润问题1．文星商店以每支4元的价格进100支钢笔，卖出时每支的标价6元，当卖出一部分钢笔后，剩余的打9折出售，卖完时商店赢利188元，其中打9折的钢笔有几支? 【答案与解析】解：设打折的钢笔有x 支，则有： 6(100-x )+6×90%x ＝100×4+188 解得x ＝20答：打9折的钢笔有20支．。
一元一次方程与实际问题(1) ——和差倍分问题教学目
标
一、知识与技能：
1. 掌握一元一次方程的基本解法，理解方程的根的概念。
2. 学会解决和差倍分问题，理解这类问题的基本结构和解题思路。
3. 培养分析和解决问题的能力，提高数学应用意识。
二、过程与方法：
1. 通过实际问题的解决，体验数学建模的思想，掌握运用一元一次方程解决实际问题的基本方法。
2. 培养学生的观察、归纳和概括能力，以及从特例到一般的归纳推理方法。
3. 在解题过程中，学会与他人合作交流，养成独立思考与合作学习的习惯。
三、情感态度与价值观：
1. 感受数学与生活的紧密联系，激发学习数学的兴趣和探究欲望。
2. 培养学生积极向上的情感和态度，形成正确的价值观。
3. 通过解题过程，培养学生的团队合作精神和沟通表达能力。
四、教学重点与难点：
重点：一元一次方程的解法，和差倍分问题的建模与解决。
难点：如何根据实际问题建立一元一次方程模型，如何理解并运用和差倍分问题的关系式。
五、教学评价：
1. 通过课堂观察、作业检查和测试等方式评价学生的学习效果。
2. 重视过程评价，关注学生在学习过程中的表现和进步。
3. 运用多种评价方式，以鼓励和激励为主，帮助学生树立信心，提高学习积极性。
5.4一元一次方程的应用——和差倍分问题教学实录石家庄市第四十九中学薛晓丽一、教学目标：（一）知识目标：根据实际问题中数量关系列方程解决问题。
掌握列方程解决实际问题的一般步骤．（二）能力目标：培养学生数学建模能力，发现和提出问题、分析和解决问题的能力．（三）情感目标：增强数学的应用意识和学习数学的兴趣，积累数学活动经验.二、教学重点和难点重点：寻找实际问题中的等量关系，建立数学模型；培养学生发现、解决问题的能力。
难点：根据实际问题分析数量关系列出方程.三、教学方法：自主学习与小组合作相结合四、教学过程：教学环节教学设计设计意图创设情境提出问题师：前面学习了那些用代数式表示的实际问题？生：增长率、工作量、行程问题……师:展示图片，生活很多问题都可以用方程来解决，今天我们一起来学习一元一次方程的应用。
（板书课题）激发学生的学习兴趣。
教学过程自主探究活动1：学生植树的图片引出问题某校七年级同学参加这一次公益活动，其中15%的同学去作保护环境的宣传，剩下的170名同学去植树、种草。
七年级共有多少名同学参加这次公益活动？师：4、5、6组同学板演，分工如下：1．探究：8号：①七年级同学参加公益活动做了件事：分别是，15%的同学去作，170名同学作，7号：②设七年级共有名同学参加公益活动。
x6号：③请用文字叙述等量关系并列出方程：5号：④写出本题的规范过程：作环保宣传的同学/名植树种草的同学/名参加公益活动的同学/名x让学生充分发挥主体作用，自己去观察、探究，解决问题。
师：1、2号组长纠错后，5组5-8号同学讲解。
（边讲解边说明注意的问题）解得： 6x =2113x +=答：小拖拉机一天耕地6公顷，大拖拉机一天耕地13公顷。
解法二：设大拖拉机一天耕地公顷，x 解得： 2(19)1x x =-+13x =196x -=答：小拖拉机一天耕地6公顷，大拖拉机一天耕地13公顷。
解法三：设小拖拉机一天耕地公顷，大拖拉机一天耕地公顷，x x 1921x y y x +=⎧⎨=+⎩613x y =⎧⎨=⎩答：小拖拉机一天耕地6公顷，大拖拉机一天耕地13公顷。
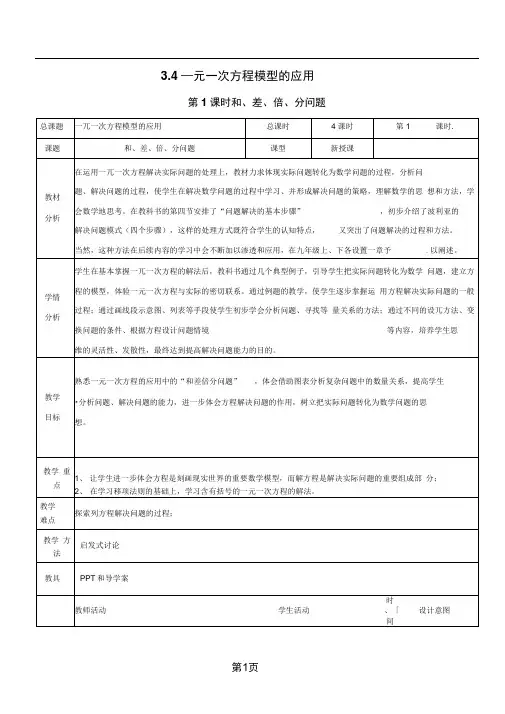
第三章一元一次方程3.4 实际问题与一元一次方程第1课时产品配套问题和工程问题学习目标：1. 理解配套问题、工程问题的背景.2. 分清有关数量关系，能正确找出作为列方程依据的主要等量关系.3. 掌握用一元一次方程解决实际问题的基本过程.重点：掌握用一元一次方程解决实际问题的基本过程.难点：能够准确找出实际问题中的等量关系，并建立模型解决问题.一、要点探究探究点1：产品配套问题填一填：1.某厂欲制作一些方桌和椅子，1张方桌与4把椅子刚好配成一套，为了使桌椅刚好配套，商家应制作椅子的数量是桌子数量的___ 倍. 方桌与椅子的数量之比是.2.一个油桶由两个圆形铁片和一个长方形铁片相配套．某车间有工人42人，每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片．设安排x名工人生产圆形铁片，可使圆形铁片和长方形铁片刚好配套，请填写下表：等量关系：（1）每小时生产的圆形铁片=_____×每小时生产的长方形铁片.（2）生产的套数相等.方法总结：生产调配问题通常从调配后各量之间的倍、分关系寻找相等关系，建立方程.解决配套问题的思路：1.利用配套问题中物品之间具有的数量关系作为列方程的依据；2.利用配套问题中的套数不变作为列方程的依据.例1 如图，足球是由32块黑白相间的牛皮缝制而成的，黑皮可看作正五边形，白皮可看作正六边形，求白皮、黑皮各多少块？（提示：一块白皮（六边形）中，有三边与黑皮（五边形）相连，因此白皮边数是黑皮边数的2倍）针对训练部分工人生产螺栓，其他部分工人生产螺母，恰好每天生产的螺栓螺母：按1：3配套．若2.一套仪器由一个A部件和三个B部件构成. 用1立方米钢材可做40个A部件或240个B 部件. 现要用6立方米钢材制作这种仪器，应用多少钢材做A部件，多少钢材做B部件，才能恰好配成这种仪器？共配成多少套？探究点2：工程问题填一填一件工作，甲独做需要6天完成，乙独做需要5天完成.(1)若把工作总量设为1，则甲的工作效率（甲一天完成的工作量）是，乙的工作效率是.(2）甲做x天完成的工作量是，乙做x天完成的工作量是，甲乙合做x天完成的工作量是 .议一议工程问题中，涉及哪些量？它们之间有什么数量关系？（1）工程问题中，涉及的量有工作量、_________________________________________;（2）请写出这些量之间存在的数量关系：_____________________________________________________________________________.例2加工某种工件，甲单独作要20天完成，乙只要10天就能完成任务，现在要求二人在12天内完成任务．问乙需工作几天后甲再继续加工才可正好按期完成任务？【提示：可运用表格列出题中存在的各种量.】想一想：若要求二人在8天内完成任务，乙先加工几天后，甲加入合作加工，恰好能如期完成任务？要点归纳：解决工程问题的基本思路：1. 三个基本量：工作量、工作效率、工作时间. 它们之间的关系是：工作量 = 工作效率×工作时间；合作的工作效率 =工作效率之和. 2. 相等关系：工作总量=各部分工作量之和=合作的工作效率×工作时间. 3. 通常在没有具体数值的情况下，把工作总量看作“1”. 针对训练一条地下管线由甲工程队单独铺设需要12天，由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工，要多少天可以铺好这条管线？二、课堂小结用一元一次方程解决实际问题的基本过程如下：实际问题一元一次方程的解(x =a )设未知数，列方程检验1. 某人一天能加工甲种零件50个或加工乙种零件20个，1个甲种零件与2个乙种零件配成一套，30天制作最多的成套产品，若设x天制作甲种零件，则可列方程为.2.一项工作，甲独做需18天，乙独做需24天，如果两人合做8天后，余下的工作再由甲独做x天完成，那么所列方程为.3.某家具厂生产一种方桌，1立方米的木材可做50个桌面或300条桌腿，现有10立方米的木材，怎样分配生产桌面和桌腿使用的木材，才能使桌面、桌腿刚好配套，共可生产多少张方桌？(一张方桌有1个桌面，4条桌腿)4.一项工作，甲单独做20小时完成，乙单独做12小时完成，现在先由甲单独做4小时，剩下的部分由甲、乙合做. 剩下的部分需要几小时完成？5. 一个道路工程，甲队单独施工9天完成，乙队单独做24天完成．现在甲、乙两队共同施工3天，因甲另有任务，剩下的工程由乙队完成，问乙队还需几天才能完成？参考答案课堂探究一、要点探究解：设足球上黑皮有x块，则白皮为(32-x)块，五边形的边数共有5x条，六边形边数有6(32-x)条．依题意,得2×5x=6（32-x）,解得x=12，则32-x=20.答：白皮20块，黑皮12块.【针对训练】1. 12x×3＝18×(30−x)2.解：设应用 x 立方米钢材做 A 部件，则应用(6－x)立方米做 B 部件.根据题意，列方程：3×40x = (6－x)×240.解得x = 4.则6－x = 2.共配成仪器：4×40=160 (套). 答：应用 4 立方米钢材做 A 部件， 2 立方米钢材做 B 部件，共配成仪器 160 套.填一填（1议一议（1）工作效率、工作时间（2）工作量=工作效率×工作时间例2 解：解：设乙需工作x天后甲再继续加工才可正好按期完成任务，则甲做了（12-x）天.依题意，得11(12) 1.2010x x-+=解得x=8. 答：乙需工作8天后甲再继续加工才可正好按期完成任务.想一想：解：设甲加工y天，两人如期完成任务，则在甲加入之前，乙先工作了(8-y)天.依题意，得18 1.2010y +=解得y =4. 答：乙需加工4天后,甲加入合作加工才可正好按期完任务.【针对训练】解：设要 x 天可以铺好这条管线，由题意得：11 1.1224x x +=解方程，得x = 8. 答：要8天可以铺好这条管线. 当堂检测1. 2×50x = 20(30－x)2.88++1182418x= 3. 解：设用 x 立方米的木材做桌面，则用 (10－x) 立方米的木材做桌腿.根据题意，得 4×50x = 300(10－x)，解得x =6，所以 10－x = 4，可做方桌为50×6=300(张). 答：用6立方米的木材做桌面，4立方米的木材做桌腿，才能使桌面、桌腿刚好配套，可做)+ 1.12xx =13+(3+) 1.24x =解得x = 13. 答：乙队还需13天才能完成．第三章 一元一次方程3.4 实际问题与一元一次方程第2课时 销售中的盈亏学习目标：1. 理解商品销售中的相关概念及数量关系.2. 根据商品销售中的数量关系列一元一次方程解决与打折销售有关的实际 问题，并掌握解此类问题的一般思路. 重点：掌握商品销售中成本（进价）、售价（卖价）、标价（原价）、利润、利润率、折扣等量之间的数量关系，知道销售中的盈亏取决于售价与成本之差.难点：能够通过自主分析，建立一元一次方程模型解决同类型问题，并掌握解此类问题 的一般思路.一、要点探究探究点：销售中的盈亏 合作探究：连一连：正确理解销售问题中的几个重要概念进价 也称成交价，是商店销售商品时的销售价格.标价 商店销售商品时所赚的钱. 售价 商店购进商品时的价格.利润 商店销售商品时标出的价格，也称定价. 填一填1. 商品原价200元，九折出售，卖价是 元.2. 商品进价是150元，售价是180元，则利润是 元，利润率是_____.3. 某商品原来每件零售价是a 元，现在每件降价10%，降价后每件零售价是 元.4. 某种品牌的彩电降价20%以后，每台售价为a 元，则该品牌彩电每台原价应为 元.5. 某商品按定价的八折出售，售价是12.8元，则原定售价是 元. 想一想：以上问题中有哪些量?你能说出它们之间的关系吗？要点归纳：销售问题中的常用数量关系：●售价、进价、利润的关系：商品利润= 商品售价－商品进价； ●进价、利润、利润率的关系：利润率=％商品进价商品利润100 ；●标价、折扣数、商品售价的关系：商品售价=标价×10折扣数； ●商品售价、进价、利润率的关系：商品售价=商品进价×（1+利润率）. 议一议：销售中存在盈亏，说一说销售盈亏中存在哪几种可能情况,并分别说明在该种情况下，售价与进价的大小.（1）盈利：售价 进价（填“＞”、“＜”或“=”），此时，利润 0（填“＞”“＜”或“=”）；（2）亏损：售价 进价（填“＞”、“＜”或“=”），此时，利润 0（填“＞”“＜”或“=”）；（3）不盈不亏：售价 进价（填“＞”、“＜”或“=”），此时，利润 0（填“＞”、 “＜”或“=”）.例1 一商店在某一时间以每件60元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，卖这两件衣服总的是盈利还是亏损，或是不盈不亏?要点归纳：销售的盈亏取决于总售价与总成本之间的关系：总售价 ＞ 总成本时，盈利；总售价＜总成本时，亏损；总售价＝总成本时，不盈不亏.针对训练1.某琴行同时卖出两台钢琴，每台售价为960元. 其中一台盈利20%，另一台亏损20%.这次琴行是盈利还是亏损，或是不盈不亏？2.某文具店有两个进价不同的计算器都卖64元，其中一个盈利60%，另一个亏本20%.请通过计算说明这次交易中的盈亏情况.例2某商品的零售价是900元，为适应竞争，商店按零售价打9折（即原价的90%），并再让利40元销售，仍可获利10%，求该商品的进价．方法归纳：利用一元一次方程解决销售问题时，熟练、准确地运用销售问题中常用的等量关系是解题的关键.针对训练1.某商场把进价为1980元的商品按标价的八折出售，仍获利10%，则该商品的标价为元.2.我国政府为解决老百姓看病难的问题，决定下调药品的价格，某种药品在2005年涨价30%后，2007降价70%至a元，则这种药品在2005年涨价前价格为元.二、课堂小结●售价、进价、利润的关系：商品利润= 商品售价－商品进价●进价、利润、利润率的关系：利润率=％商品进价商品利润100 ●标价、折扣数、商品售价的关系：商品售价=标价×10折扣数●商品售价、进价、利润率的关系：商品售价=商品进价×（1+利润率）1.某种商品的进价为每件a 元，零售价为每件90元，若商品按八五折出售，仍可获利10%，则下列方程正确的是（ ）A ．85%a=10%×90B ．90×85%×10%=aC ．85%(90-a)=10%D ．(1+10%)a=90×85%2.两件商品都卖120元，其中一件赢利25%，另一件亏本20%，则两件商品卖出后（ ） A ．赢利16元 B ．亏本16元 C ．赢利6元 D ．亏本6元3.某种商品因换季准备打折出售，如果按原定价的七五折出售，将赔25元，而按原定价的九折出售，将赚20元，则这种商品的原价是（ ） A ．500元 B ．400元 C ．300元 D ．200元4.某商品的进价是1000元，售价是1500元，由于销售情况不好，商店决定降价出售， 但又要保证利润率不低于5%，那么商店最多可打几折出售此商品？5.据了解个体商店销售中售价只要高出进价的20% 便可盈利，但老板们常以高出进价50%~100% 标价，假若你准备买一双标价为600元的运动鞋，应在什么范围内还价？参考答案课堂探究一、要点探究连一连：进价也称成交价，是商店销售商品时的销售价格.标价商店销售商品时所赚的钱.售价商店购进商品时的价格.利润商店销售商品时标出的价格，也称定价.填一填：1.1802. 30 20%3.0.9a4.1.25a5.16议一议：(1)＞＞（2）＜＜（3）= =解：设盈利25%的那件衣服的进价是x元，根据进价与得润的和等于售价列得方程：x+0.25x=60，解得x=48，类似地，设另一件亏损衣服的进价为y元，它的商品利润是-25%y元，列方程y+（-25%y）=60，解得y=80．那么这两件衣服的进价是x+y=128元，而两件衣服的售价为120元，120-128=-8元，所以这两件衣服亏损8元．【针对训练】1.解：设盈利20%的钢琴的成本为x元，x（1+20%）=960，解得x=800.设亏本20%的钢琴的成本为y元，y（1-20%）=960，解得y=1200.所以960×2-（800+1200）=-80，所以亏损80元．这次琴行亏本80元.2. 解：根据题意得：64-64÷（1+60%）+64-64÷（1-20%）=64-40+64-80=8（元）．所以这次交易盈利8元.设盈利60%的计算器的成本为x 元，x （1+60%）=64，解得x=40.设亏本20%的计算器的成本为y 元，y （1-20%）=64，解得y=80.所以64×2-（40+80）=8（元），所以这次交易盈利8元．解：设该商品的进价为每件 x 元，依题意，得 900×0.9－40＝10% x ＋x ， 解得x ＝700.答：该商品的进价为700元．【针对训练】1.2722.5 2.10039a 当堂检测1. D2.D3.C4.解：设商店最多可以打x 折出售此商品，根据题意，得15001000(15).10x ⨯=+％ 解得x = 7. 答:商店最多可以打7折出售此商品.5. 解：答：应在360元~480元内还价.。
可编辑修改精选全文完整版实际问题与一元一次方程【学习目标】1.熟练掌握分析解决实际问题的一般方法及步骤；2.熟悉行程，工程，配套及和差倍分问题的解题思路．【要点梳理】要点一、用一元一次方程解决实际问题的一般步骤列方程解应用题的基本思路为：问题−−−→分析抽象方程−−−→求解检验解答．由此可得解决此类题的一般步骤为：审、设、列、解、检验、答．要点诠释：（1）“审”是指读懂题目，弄清题意，明确哪些是已知量，哪些是未知量，以及它们之间的关系，寻找等量关系；（2）“设”就是设未知数，一般求什么就设什么为x ，但有时也可以间接设未知数；（3）“列”就是列方程，即列代数式表示相等关系中的各个量，列出方程，同时注意方程两边是同一类量，单位要统一；（4）“解”就是解方程，求出未知数的值；（5）“检验”就是指检验方程的解是否符合实际意义，当有不符合的解时，及时指出，舍去即可；（6）“答”就是写出答案，注意单位要写清楚．要点二、常见列方程解应用题的几种类型1．和、差、倍、分问题（1）基本量及关系：增长量＝原有量×增长率，现有量＝原有量+增长量，现有量＝原有量-降低量．（2）寻找相等关系：抓住关键词列方程，常见的关键词有：多、少、和、差、不足、剩余以及倍，增长率等．2．行程问题（1）三个基本量间的关系： 路程=速度×时间（2）基本类型有：①相遇问题（或相向问题）：Ⅰ．基本量及关系：相遇路程=速度和×相遇时间Ⅱ．寻找相等关系：甲走的路程+乙走的路程＝两地距离．②追及问题：Ⅰ．基本量及关系：追及路程=速度差×追及时间Ⅱ．寻找相等关系：第一，同地不同时出发：前者走的路程＝追者走的路程； 第二，同时不同地出发：前者走的路程+两者相距距离＝追者走的路程． ③航行问题：Ⅰ．基本量及关系：顺流速度=静水速度+水流速度，逆流速度=静水速度－水流速度， 顺水速度－逆水速度＝2×水速；Ⅱ．寻找相等关系：抓住两地之间距离不变、水流速度不变、船在静水中的速度不变来考虑．（3）解此类题的关键是抓住甲、乙两物体的时间关系或所走的路程关系，并且还常常借助画草图来分析．3．工程问题如果题目没有明确指明总工作量，一般把总工作量设为1．基本关系式：（1）总工作量=工作效率×工作时间；（2）总工作量=各单位工作量之和．4．调配问题寻找相等关系的方法：抓住调配后甲处的数量与乙处的数量间的关系去考虑．5．利润问题 (1) =100% 利润利润率进价(2) 标价＝成本(或进价)×(1＋利润率)(3) 实际售价＝标价×打折率(4) 利润＝售价－成本(或进价)＝成本×利润率注意：“商品利润＝售价－成本”中的右边为正时，是盈利；当右边为负时，就是亏损.打几折就是按标价的十分之几或百分之几十销售．6．存贷款问题（1）利息=本金×利率×期数（2）本息和（本利和）＝本金＋利息＝本金＋本金×利率×期数＝本金×(1＋利率×期数)（3）实得利息=利息-利息税（4）利息税=利息×利息税率（5）年利率＝月利率×12（6）月利率＝年利率×121 7.数字问题已知各数位上的数字，写出两位数，三位数等这类问题一般设间接未知数，例如：若一个两位数的个位数字为a ，十位数字为b ，则这个两位数可以表示为10b+a ．选择设计方案的一般步骤：（1）运用一元一次方程解应用题的方法求解两种方案值相等的情况．（2）用特殊值试探法选择方案，取小于（或大于）一元一次方程解的值，比较两种方案的优劣性后下结论．【典型例题】类型一、和差倍分问题例1．旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%，第二次旅程中用去剩余汽油的40%，这样油箱中剩的汽油比两次所用的汽油少1公斤，求油箱里原有汽油多少公斤？等量关系为：油箱中剩余汽油+1=用去的汽油.【变式】某班举办了一次集邮展览，展出的邮票若平均每人3张则多24张，若平均每人4张则少26张，这个班有多少学生?一共展出了多少张邮票?类型二、行程问题1.车过桥问题例2.某桥长1200m，现有一列匀速行驶的火车从桥上通过，测得火车从上桥到完全过桥共用了50s，而整个火车在桥上的时间是30s，求火车的长度和速度．注：火车“完全过桥”和“完全在桥上”是两种不同的情况，借助线段图分析如下(注：A点表示火车头)：(2)火车完全在桥上如图(2)所示，此时火车走的路程是桥长－车长．由于火车是匀速行驶的，所以等量关系是火车从上桥到完全过桥的速度＝整个火车在桥上的速度．【变式】某要塞有步兵692人，每4人一横排，各排相距1米向前行走，每分钟走86米，通过长86米的桥，从第一排上桥到排尾离桥需要几分钟？2.相遇问题（相向问题）例3．小李骑自行车从A地到B地，小明骑自行车从B地到A地，两人都匀速前进.已知两人在上午8时同时出发，到上午10时，两人还相距36千米，到中午12点，两人又相距36千米.求A、B两地间的路程.【变式】甲、乙两辆汽车分别从A、B两站同时开出，相向而行，途中相遇后继续沿原路线行驶，在分别到达对方车站后立即返回，两车第二次相遇时距A站34km，已知甲车的速度是70km/h，乙车的速度是52km/h，求A、B两站间的距离.3.追及问题（同向问题）例4．一辆卡车从甲地匀速开往乙地，出发2小时后，一辆轿车从甲地去追这辆卡车，轿车的速度比卡车的速度每小时快30千米，但轿车行驶一小时后突遇故障，修理15分钟后，又上路追这辆卡车，但速度减小了13，结果又用两小时才追上这辆卡车，求卡车的速度．4.航行问题（顺逆风问题）例5．盛夏，某校组织长江夜游，在流速为2.5千米/时的航段，从A地上船，沿江而下至B地，然后溯江而上到C地下船，共乘船4小时．已知A、C两地相距10千米，船在静水中的速度为7.5千米/时，求A、B 两地间的距离．【点评】这是航行问题，本题需分类讨论，采用“线示”分析法画出示意图(如下图所示)，然后利用“共乘”4小时构建方程求解．5.环形问题例6．环城自行车赛，最快的人在开始48分钟后遇到最慢的人，已知最快的人的速度是最慢的人速度的72倍，环城一周是20千米，求两个人的速度.相等关系为：最快的人骑的路程-最慢人骑的路程=20千米.【变式】两人沿着边长为90m的正方形行走，按A→B→C→D→A…方向，甲从A以65m/min的速度，乙从B 以72m/min的速度行走，如图所示，当乙第一次追上甲时，在正方形的哪一条边上?类型三、工程问题例7．一个蓄水池有甲、乙两个进水管和一个丙排水管，单独开甲管6小时可注满水池；单独开乙管8小时可注满水池，单独开丙管9小时可将满池水排空，若先将甲、乙管同时开放2小时，然后打开丙管，问打开丙管后几小时可注满水池?相等关系：甲、乙开2h的工作量+甲、乙、丙水管的工作量=1．【变式】收割一块水稻田，若每小时收割4亩，预计若干小时完成，收割23后，改用新式农机，工作效率提高到原来的112倍，因此比预计时间提早1小时完成，求这块水稻田的面积．类型四、配套问题（比例问题、劳动力调配问题）例8．某工程队每天安排120个工人修建水库，平均每天每个工人能挖土5 m3或运土3 m3，为了使挖出的土及时被运走，问：应如何安排挖土和运土的工人?【变式】某商店选用A、B两种价格分别是每千克28元和每千克20元的糖果混合成杂拌糖果后出售，为使这种杂拌糖果的售价是每千克25元，要配制这种杂拌糖果100千克，问要用这两种糖果各多少千克？类型五、利润问题例9．以现价销售一件商品的利润率为30%，如果商家在现有的价格基础上先提价40%，后降价50%的方法进行销售，商家还能有利润吗？为什么？【变式1】某个商品的进价是500元，把它提价40%后作为标价.如果商家要想保住12%的利润率搞促销活动，请你计算一下广告上可写出打几折？【变式2】张新和李明相约到图书大厦去买书，请你根据他们的对话内容(如图所示)，求出李明上次所买书籍的原价．类型六、存贷款问题例10．爸爸为小强存了一个五年期的教育储蓄，年利率为2.7％，五年后取出本息和为17025元，爸爸开始存入多少元.类型七、数字问题例11．一个三位数，十位上的数是百位上的数的2倍，百位、个位上的数的和比十位上的数大2，又个位、十位、百位上的数的和是14，求这个三位数.【变式】一个两位数，个位上的数字比十位上的数字大4，这个两位数又是这两个数字的和的4倍，求这个两位数.类型八、方案设计问题例12．为鼓励学生参加体育锻炼．学校计划拿出不超过1600元的资金再购买一批篮球和排球．已知篮球和排球的单价比为3:2，单价和为80元．(1)篮球和排球的单价分别是多少元?(2)若要求购买的篮球和排球的总数量是36个，且购买的篮球数量不少于26个．请探究有哪几种购买方案?【变式】某校组织10位教师和部分学生外出考察，全程票价为25元，对集体购票，客运公司有两种优惠方案可供选择：方案一：所有师生按票价的88%购票；方案二：前20人购全票，从第21人开始，每人按票价的80%购票．(1)若有30位学生参加考察，问选择哪种方案更省钱?(2)参加考察的学生人数是多少时，两种方案车费一样多?【课堂练习】1．某校用56m长的篱笆围成一个长方形的生物园，要使长为16 m，则宽为________m．2．小明和他父亲的年龄之和为54，又知父亲年龄是小明年龄的3倍少2岁，则他父亲的年龄为____岁．3. 甲、乙二人在长为400米的圆形跑道上跑步，已知甲每秒钟跑9米，乙每秒钟跑7米．（1）当两人同时同地背向而行时，经过________秒钟两人首次相遇；（2）两人同时同地同向而行时，经过________秒钟两人首次相遇．4．某项工作甲单独做4天完成，乙单独做6天完成，若甲先干一天，然后，甲、乙合作完成此项工作，若设甲一共做了x天，乙工作的天数为________，由此可列出方程________________．5. A、B两地相距216千米，甲、乙分别在A、B两地，若甲骑车的速度为15千米/时，乙骑车的速度为12千米/时。
