下载文档原格式
可编辑修改精选全文完整版课题:一元一次方程的应用——和差倍分问题 含答案问题情境：由各部分之间的和差倍分关系，求全体 问题模型：已知各段路与全路之间的和差倍分关系，求全路的长度求解模型：1.设全路的长为x 千米；2.根据各段路与全路之间的和差倍分关系，用含x 的代数式表示各个路段；3.根据关系式“第一工程队筑路数＋第二工程队筑路数＋第三工程队筑路数=全路的总长”，列出方程；4.求出方程的解，并代入验证。
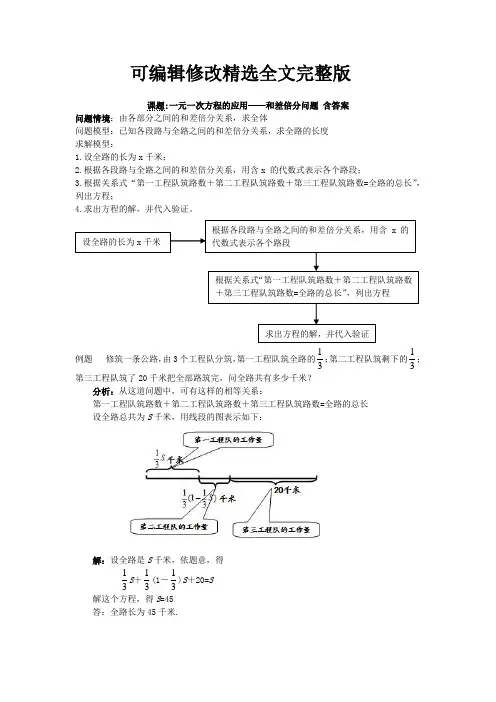
例题 修筑一条公路，由3个工程队分筑，第一工程队筑全路的13；第二工程队筑剩下的13；第三工程队筑了20千米把全部路筑完，问全路共有多少千米？分析：从这道问题中，可有这样的相等关系：第一工程队筑路数＋第二工程队筑路数＋第三工程队筑路数=全路的总长设全路总共为S 千米，用线段的图表示如下：解：设全路是S 千米，依题意，得13S ＋13(1－13)S ＋20=S 解这个方程，得S =45答：全路长为45千米.设全路的长为x 千米 根据各段路与全路之间的和差倍分关系，用含x 的代数式表示各个路段 根据关系式“第一工程队筑路数＋第二工程队筑路数＋第三工程队筑路数=全路的总长”，列出方程 求出方程的解，并代入验证变式练习:1.（2012云南省）某企业为严重缺水的甲、乙两所学校捐赠矿泉水共2000件.已知捐给甲校的矿泉水件数比捐给乙校件数的2倍少400件.求该企业分别捐给甲、乙两所学校的矿泉水各多少件？【答案】解：设该企业分别捐给乙所学校的矿泉水x 件，则甲所学校的矿泉水是(2400)x -；根据题意得：24002000x x -+=解得x =800则甲所学校的矿泉水是(2400)28004001200x -=⨯-=答：该企业分别捐给甲、乙两所学校的矿泉水各1200件、800件。
2. （2012广西柳州）列方程解应用题：今年“六·一”儿童节，张红用8.8元钱购买了甲、乙两种礼物，甲礼物每件1.2元，乙礼物每件0.8 元，其中甲礼物比乙礼物少1件，问甲、乙两种礼物各买了多少件？ 解：设张红购买甲礼物x 件，则购买乙礼物1x +件，依题意，得：【答案】 1.20.8(1)8.8x x ++=解得：4x =则：甲为4件，乙为5件3. （2012湖南邵阳） 2012年，某地开始实施农村义务教育学校营养计划——“蛋奶工程”. 该地农村小学每份营养餐的标准是质量为300克，蛋白质含量为8%，包括一盒牛奶、一包饼干和一个鸡蛋.已知牛奶的蛋白质含量为5%，饼干的蛋白质含量为12.5%，鸡蛋的蛋白质含量为15%，一个鸡蛋的质量为60克。
一元一次方程应用题——和、差、倍、分问题一、学习重点：这类问题主要应搞清各量之间的关系，注意关键词语。
仔细读题，找出表示和、差、倍、分关系的关键字，例如：“大，小，多，少，增加，减少……”，并据题意设出未知数，利用这些关键字表示出含有未知数的量，最后利用题目中的量与量之间的关系列出方程。
1、倍数关系：通过关键词语“是几倍，增加几倍，增加到几倍，增加百分之几……”来体现。
2、多少关系：通过关键词语“多、少、和、差……”来体现。
增长量＝原有量×增长率现在量＝原有量＋增长量一般设未知数要找跟所有关系联系最紧密的那个量。
二、基础练习题：1、a比b多5，则a=______；a比b少3，则a=______；a是b的2倍，则a=____；a增加3倍，则a=_____；a增加到3倍，则a=_____；将a增加b，则a=_____；将a增加到b，则a=_____。
2、已知甲数比乙数小12，甲乙两数的和为50，甲数为_____；乙数为_____。
3、已知甲数比乙数的3倍多12，甲乙两数的和是60，甲数为_____；乙数为_____。
4、已知甲数是10，增加40%后甲数为______；在此基础上减少50%后甲数为_______。
5、已知甲数的3倍是乙数与-2的和的2倍，甲数与乙数的差为5，甲数为_____；乙数为_____。
6、三个连续偶数的和是360，中间的偶数为_____。
7、三个连续奇数的和为361，中间的奇数为_____。
8、甲班有a人，乙班的人数是甲班人数的2倍少b人，则乙班的人数为_________。
9、某校共有学生1049人，女生占男生的40%，则男生的人数为__________。
例题1:禽养场养鸡和鸭共4600只，养的鸡比鸭的4倍还多100只，禽养场的鸡鸭各多少只？练习:足球的表面是由一些呈多边形的黑白皮块缝合而成的，共计有32块，已知黑色皮块数比白色皮块数的一半多2，问两种皮块各有多少？做题：10、11例题2：一根电线长240米，把它截成三段，使第一段比第二段长20米，第三段长是第一段的2倍。
一元一次方程的应用一、和、差、倍、分问题：1.某校初三年级甲、乙两班学生人数相等，甲班男女人数之比为4：5，乙班男生人数占全班人数的60%，假设把甲乙两班合成一个新团队，那么新团队男生人数比女生人数多4人，求新团队总人数．2.一群学生前往位于青田县境内的滩坑电站建立工地进展社会实践活动，男生戴白色平安帽，女生戴红色平安帽.休息时，他们坐在一起，大家发现了一个有趣的现象，每位男生看到白色的平安帽和红色的一样多，而每位女同学看到白色的平安帽是红色的平安帽的2倍.求这群学生的总人数.3.目前XX市小学和初中在任校生共有约128万人，其中小学生在校人数比初中生在校人数的2倍多14万人(数据来源：2005学年度XX市教育统计手册)．(1)求目前XX市在校的小学生人数和初中生人数；(2)假设今年小学生每人需交杂费500元，初中生每人需交杂费1000元，而这些费用全部由XX市政府拨款解决，那么XX市政府要为此拨款多少?4.某城市现有42万人口,方案一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,求这个城市现有的城镇人口数和农村人口数.二、劳力调配问题：12多28人,因有紧急任务,需从乙队抽调21 某公司有两个工程队,甲工程队人数比乙工程队人数的2到甲队,这时甲队人数刚好是乙队人数的3,问该公司两个工程队共有多少人?三、配套问题：1.箭鹿服装厂要生产某种型号学生服一批,每3米长的某种布料可以做上衣2件或裤子3条,一件上衣和一条裤子为一套,方案用600米长的这种布料生产学生服,应分别用多少布料生产上衣和裤子,才能恰好配套?共能生产多少套?2.某车间有技术工人85人，平均每人每天可加工甲种部件16个或乙种部件10个，两个甲种部件和三个乙种部件配成一套，问加工甲、乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套？四、等积变形问题：在一只底面直径为30厘米，高为8厘米的圆锥形容器中倒满水，然后将水倒入一只底面直径为10厘米的圆柱形空容器里，圆柱形容器中的水有多高？五、行程问题：1.某人从家里骑自行车到学校。
