初中数学_课本知识点图集
- 格式:pptx
- 大小:12.04 MB
- 文档页数:58

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
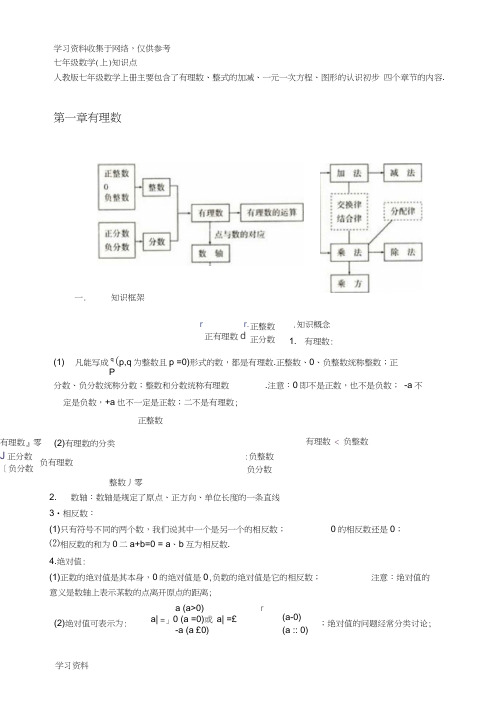
第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数。
正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数。
注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线。
3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6。
互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数。
7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数。
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步 四个章节的内容.第一章有理数一.知识框架.知识概念1. 有理数:(1) 凡能写成q (p,q 为整数且p =0)形式的数,都是有理数.正整数、0、负整数统称整数;正P分数、负分数统称分数;整数和分数统称有理数 .注意:0即不是正数,也不是负数; -a 不定是负数,+a 也不一定是正数;二不是有理数;正整数整数丿零2. 数轴:数轴是规定了原点、正方向、单位长度的一条直线3•相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;⑵相反数的和为0二a+b=0 = a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;rr. 正有理数d 正整数正分数(2)有理数的分类有理数』零 负有理数有理数 < 负整数:负整数 负分数J 正分数[负分数(2)绝对值可表示为:a (a>0)ra| =」0 (a =0)或 a| =£-a (a £0)(a-0)(a :: 0);绝对值的问题经常分类讨论;5•有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数V 0.1 6•互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若0,那么a的倒数是,a 若ab=1二a、b互为倒数;若ab=-1:= a、b互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3 )一个数与0相加,仍得这个数.8. 有理数加法的运算律:(1 )加法的交换律:a+b=b+a ; ( 2)加法的结合律:(a+b) +c=a+ (b+c).9. 有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+ (-b).10有理数乘法法则:(1 )两数相乘,同号为正,异号为负,并把绝对值相乘;(2) 任何数同零相乘都得零;(3) 几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11有理数乘法的运算律:(1 )乘法的交换律:ab=ba; (2)乘法的结合律:(ab) c=a (bc);(3 )乘法的分配律: a (b+c) =ab+ac .12 •有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,即a无意义.13. 有理数乘方的法则:(1)正数的任何次幕都是正数;(2)负数的奇次幕是负数;负数的偶次幕是正数;注意:当n为正奇数时:(-a)n=-a n或(a-b)n=-(b-a)n ,当n 为正偶数时:(-a)n =a n或(a-b)n=(b-a)n .14. 乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幕;15 •科学记数法:把一个大于10的数记成a x 10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16. 近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17. 有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18. 混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。

初中知识点总结图集一、数学1. 整数整数是由零、正整数和负整数组成的,表示数轴上的位置。
整数有加法、减法、乘法、除法等运算。
2. 分数分数是指一个整数除以另一个整数所得到的结果,通常以分数线分开分子和分母。
分数有加法、减法、乘法、除法等运算。
3. 代数代数是运用字母表示数或数量的一种数学分支。
代数包括多项式、方程、不等式等内容,是数学学习的重要部分。
4. 几何几何是研究空间与图形的数学分支,主要包括平面几何和立体几何。
几何学可以帮助我们认识周围的世界,并且有着广泛的应用价值。
5. 数据数据处理包括统计和概率两大内容。
统计是研究数据的收集、整理、分析和解释,概率是研究随机事件发生的可能性。
6. 函数函数是代数学中的一个概念,用来描述自变量和因变量之间的关系。
函数包括线性函数、二次函数、指数函数等多种形式。
7. 等式与不等式等式是两个数或代数式相等的关系,不等式是两个数或代数式不等的关系。
解等式和不等式是数学学习的重要内容。
8. 图形与变换图形是平面上的点和线组成的形象,变换是指图形经过平移、旋转、翻折等操作后的新图形。
图形与变换是初中数学的难点内容。
9. 比例与百分数比例是两个量之间的相对大小关系,百分数是将整数表示为百分之几。
比例与百分数是实际生活中经常用到的数学概念。
二、物理1. 力和压强力是物体相对于其他物体的作用,压强是单位面积上受到的力的大小。
力与压强是物理学中的基本概念。
2. 运动和力的关系牛顿三定律是运动和力的基本定律,包括惯性定律、加速度定律和作用-反作用定律。
了解牛顿三定律对理解物体的运动很重要。
3. 动能和势能动能是由物体的运动产生的能量,势能是由物体的位置产生的能量。
动能和势能是物理学中的两种重要能量形式。
4. 声音和光学声音是一种机械波,光学是研究光和其它电磁波的性质和行为。
声音和光学是物理学中的两个重要分支。
5. 电学电学是研究电荷、电流、电场、电路等内容的物理学分支,包括电荷守恒定律、欧姆定律、电路的串联和并联等内容。


初中数学知识结构图193 数与代数17•有理数27、整式的加减广6•有理数的概念16.有理数的运算-21.代数式列代数式代数式的值32、一兀一次方程39、二兀一次方程组45、一元一次不等式和一元一次不等式组56、整式的乘除J63、因式分解22、23、20、24、25、26、28、29、30、31、『35、36、37、.38、-43、-1•有理数(正数与负数)2•数轴< 3•相反数4•绝对值-5•有理数从大到小比较-7•有理数的加法、加法运算律8•有理数的减法9•有理数的加减混和运算10.有理数的乘法、乘法运算I11.有理数的除法、倒数12.有理数的乘方13. 有理数的混和运算14. 科学记数法、近似数与有效数字I 15.用计算器进行简单的数的运算-18.单项式'■ 19、多项式整式的概念合并同类项去括号与添括号整式的加减法等式及其基本性质方程和方程的解、解方程一元一次方程及其解法一次方程的应用元一次方程组的解法相关概念及性质三元一次方程组及其解法举例一次方程组的应用元一次不等式兀一- --- 、44、一元一次不等式组51、整式的乘法&-61、方法62、意义47、4&49、—50、52、53、54、55、整式的除法40、一元一次不等式及其解法41、不等式的解集42、不等式和它的基本性质46、同底数幕的乘法、单项式的乘法幕的乘法、积的乘方单项式与多项式相乘多项式的乘法平方差与完全平方根多项式乘以单项式单项式除以单项式同底数幕的除法-57、提取58、运用公式法y59、分组分解法I 60、其他分解法『65、分式的乘除法一一64、分式的乘除运算J 69、可化为一元一次方程的分式方程及其应用72、分式70、分式的意义和性质J 71、分式的加减法「73、平方根与立方根75、数的开方74、实数广66、含字母系数的一元一次方程67、分式方程解法、阵根68分式方程的应用广86、二次根式的意义79、二次根式的乘除法76、193数与代数198初中数学87、102、113、二次根式V 82、二次根式的加减法I 85、二次根式的混合运算兀二次方程77、78、80、81、最简二次根式二次根式的除法二次根式的加减法二次根式的加减法同类二次根式.83、二次根式的混合运算-84、有理化因式一二次方程的解法98、一元二次方程的意义100、二元二次方程组99、*一元二次方程组的根与系数的关系94、95、93、—兀194 空间与图形126、相交、平行138、三角形<151、四边形分式方程的解法*无理方程的意义、解法分式方程、无理方程的应用97、可化为一元二次方程的分式方程式和无理方程一元二次方程的应用< 103、一次函数与一元一次不等式一次函数t104、一次函数图像的图像和性质I 105、正比例函数的图像和性质二次函数一一107二次函数的有关概念平面直角坐标系函数函数的图像反比例函数101、-106、108函数及其图像•109、110、111、112、「114、线段116、线段、角3 115、角<120、相交线96、123、117、相交线、对顶角、邻角、补角垂线、点到直线的距离同位角、内错角、同旁内角平行线概念及性质平行线的判定118、119、平行线彳121、I 122、空间直线、平面的位置关系命题、公理、定理f129、与三角形有关的边134、全等三角形135、等腰三角形133、直角三角形一一132、勾股定理131、与三角形有关的角136、轴对称137、基本作图平行四边形多边形中心对称124、125、广144、149、150、'148、梯形139、140、\ 141、142、<143、130、三角形的内角平行四边形的概念及其性质平行四边形的判定矩形的概念、性质和判定菱形的概念、性质和判定正方形的概念、性质和判定-145、梯形的相关概念-146、等腰梯形的概念、性质和判定I 147、三角形、梯形的中位线156、比例线段158、相似图形• 157、相似多边形〔155、相似三角形「159、解直角三角形厂161、解直角三角形1160、解直角三角形的应163、解直角三角形]162、锐角三角形『164、圆的有关概念及对称性165、点和圆的位置关系166、过不在同一直线上三点的圆厂172、圆的有关性质丿167、三角形的外接圆5 168、垂径定理及其逆定理169、圆心角、弧、弦、弦心距170、圆周角定理I 171、圆内接四边形及其性质「173.直线和圆的位置关系185、圆丿174.切线的判定和性质\ 177.直线和圆的位置关系Y 175.三角形的内切圆〔176. *切线长定理179.正多边形和圆一一178.正多边形的有关计算「180.圆周长、弧长183. 弧长和扇形的面积*81.圆、扇形、弓形的面积M82.圆柱和圆锥的侧面展开图、侧面积184. 圆和圆的位置关系186. 几何体、几何图形191.统计初步195.统计与概率192.概率初步Q87.平均数188. 众数和中位数189. 级差、方差、标准差^190濒数、频率、频率分布直方图概率计算196.中考复习197 .总复习「152、相似三角形的相关概念V 153、三角形相似的判定-154、相似三角形的性质198.初中数学。

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数。
正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;—a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线。
3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数。
4。
绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5。
有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6。
互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=—1⇔ a 、b 互为负倒数。
7。
有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数。
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一.知识框架二.知识概念1.有理数:(1)凡能写成)0pq,p(pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;π不是有理数;(2)有理数的分类: ①⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数②⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a、b互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a(a)0a()0a(aa或⎩⎨⎧<-≥=)0a(a)0a(aa;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0. 6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律: (1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a. 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n . 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂; 15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位. 17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
1 -七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).2 -10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
第一章、有理数第二章、整式的加减第三章、一元一次方程第四章、图形的认识初步)(无限不循环小数负无理数正无理数无理数⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧--⎩⎨⎧---)()32,21()32,21()()3,2,1()3,2,1,0(无限循环小数有限小数整数负分数正分数小数分数负整数自然数整数有理数、、 ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧实数第五章、相交线与平行线第六章、实数第七章:平面直角坐标系第八章、二元一次方程组第九章、不等式与不等式组第十章、数据的收集、整理与描述八年级数学(上)知识点第十一章:三角形全面调查抽样调查收集数据描述数据整理数据分析数据得出结论第十二章、全等三角形第十三章、轴对称第十四章、整式的乘除与分解因式 1.同底数幂的乘法法则: nm nmaa a +=⋅(m,n 都是正数)2.. 幂的乘方法则:mn n m a a =)((m,n 都是正数)⎩⎨⎧-=-).(),()(,为奇数时当为偶数时当一般地n a n a a nn n3. 整式的乘法 (1) 单项式乘法法则:单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,连同它的指数作为积的一个因式。
(2)单项式与多项式相乘:单项式乘以多项式,是通过乘法对加法的分配律,把它转化为单项式乘以单项式,即单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。
(3).多项式与多项式相乘多项式与多项式相乘,先用一个多项式中的每一项乘以另一个多项式的每一项,再把所得的积相加。
4.平方差公式: 22))((b a b a b a -=-+5.完全平方公式: 2222)(b ab a b a +±=±6. 同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即nm n m aa a -=÷ (a ≠0,m 、n 都是正数,且m>n).7.整式的除法单项式除法单项式:单项式相除,把系数、同底数幂分别相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式;多项式除以单项式: 多项式除以单项式,先把这个多项式的每一项除以单项式,再把所得的商相加. 8.分解因式:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式. 分解因式的一般方法:1. 提公共因式法2. 运用公式法3.十字相乘法 分解因式的步骤:(1)先看各项有没有公因式,若有,则先提取公因式; (2)再看能否使用公式法;(3)用分组分解法,即通过分组后提取各组公因式或运用公式法来达到分解的目的; (4)因式分解的最后结果必须是几个整式的乘积,否则不是因式分解;(5)因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.整式的乘除与分解因式这章内容知识点较多,表面看来零碎的概念和性质也较多,但实际上是密不可分的整体。