直线与圆的方程公式资料

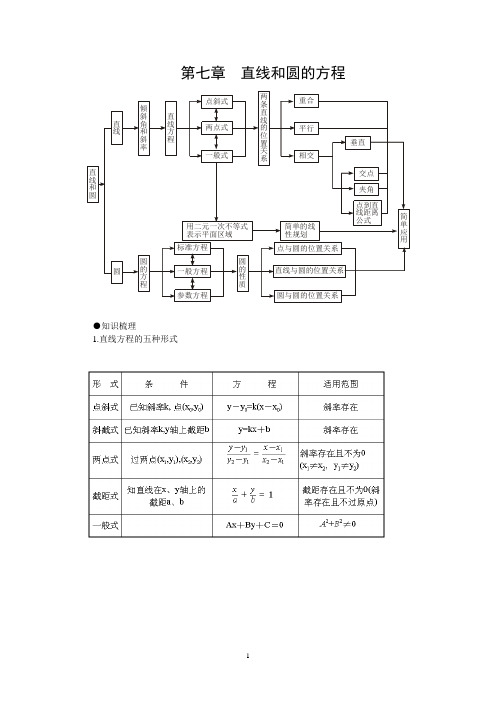
第七章直线和圆的方程●知识梳理1.直线方程的五种形式2.直线的倾斜角、斜率及直线的方向向量及位置关系:（1）直线的倾斜角在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角.直线和x 轴平行或重合时，直线的倾斜角为0°,直线倾斜角取值范围0°≤α＜180°. （2）直线的斜率倾斜角α不是90°的直线，它的倾斜角的正切叫做这条直线的斜率，常用k 表示，即k =tan α（α≠90°）.倾斜角是90°的直线没有斜率；倾斜角不是90°的直线都有斜率，其取值范围是（－∞，+∞）.（4）求直线斜率的方法①定义法：已知直线的倾斜角为α，且α≠90°，则斜率k =tan α.②公式法：已知直线过两点P 1（x 1，y 1）、P 2（x 2，y 2），且x 1≠x 2，则斜率k =1212x x y y --.平面直角坐标系内，每一条直线都有倾斜角，但不是每一条直线都有斜率. 对于直线上任意两点P 1（x 1，y 1）、P 2（x 2，y 2），当x 1=x 2时，直线斜率k 不存在，倾斜角α=90°；当x 1≠x 2时，直线斜率存在，是一实数，并且k ≥0时，α=arctan k ，k ＜0时，α=π+arctan k .（5）到角与夹角：若直线l 1, l 2的斜率分别为k 1, k 2，将l 1绕它们的交点逆时针旋转到与l 2重合所转过的最小正角叫l 1到l 2的角；l 1与l 2所成的角中不超过900的正角叫两者的夹角。

若记到角为θ，夹角为α，则tan θ=21121k k k k +-,tan α=21121k k k k +-.（6）平行与垂直：若直线l 1与l 2的斜率分别为k 1, k 2。

且两者不重合，则l 1//l 2的充要条件是k 1=k 2；l 1⊥l 2的充要条件是k 1k 2=-1。

直线与圆的公式大全总结1. 直线的一般方程直线的一般方程可以表示为：Ax+By+C=0，其中A、B和C都是常数，并且A和B不同时为零。

2. 直线的斜截式方程直线的斜截式方程可以表示为：y=mx+b，其中m是直线的斜率，b是直线与y轴的交点。

3. 直线的点斜式方程直线的点斜式方程可以表示为：y−y1=m(x−x1)，其中(x1,y1)是直线上的已知点，m是直线的斜率。

4. 直线的两点式方程直线的两点式方程可以表示为：$\\frac{x-x_1}{x_2-x_1} = \\frac{y-y_1}{y_2-y_1}$，其中(x1,y1)和(x2,y2)是直线上的两个已知点。

5. 圆的标准方程圆的标准方程可以表示为：(x−ℎ)2+(y−k)2=r2，其中(ℎ,k)是圆心的坐标，r是圆的半径。

6. 圆的一般方程圆的一般方程可以表示为：x2+y2+Dx+Ey+F=0，其中D、E和F都是常数。

7. 圆的参数方程圆的参数方程可以表示为：$x = h + r\\cos(t)$ 和 $y = k + r\\sin(t)$，其中(ℎ,k)是圆心的坐标，r是圆的半径，t是参数。

8. 直线与圆的相交关系直线与圆的相交关系根据直线和圆的方程可以进行判断。

•若直线与圆有两个交点，则直线与圆相交。

•若直线与圆相切于一个交点，则直线与圆相切。

•若直线不与圆相交且不相切，则直线与圆相离。

9. 直线与圆的求交点要求直线和圆的交点，可以将直线的方程代入圆的方程，从而得到一个关于x的二次方程。

解这个二次方程可以得到交点的x坐标，然后再代入直线的方程可以得到交点的y坐标。

10. 圆的切线方程若直线与圆相切于一个点，该直线称为圆的切线。

圆的切线方程可以通过求解直线与圆的交点，然后利用该点的斜率和切点的坐标，使用直线的点斜式方程求得。

以上是直线与圆的公式大全总结，通过不同的方程可以描述直线和圆之间的关系、位置和属性。

对于解题和几何推导有重要的作用。

直线与圆的方程公式大全在数学中，直线和圆是两个基本的几何图形。

直线由无数个点构成，而圆则由一个中心点和半径确定。

为了描述和分析直线和圆的性质，我们需要一些方程公式。

本文将为您介绍直线和圆的方程公式大全，以帮助您更好地理解它们的特性和计算方法。

直线的方程公式1. 点斜式方程直线的点斜式方程由直线上一点的坐标和直线的斜率确定。

若直线上一点为P(x1,y1)，斜率为k，则直线的点斜式方程为：y−y1=k(x−x1)2. 截距式方程直线的截距式方程由直线在x轴和y轴上的截距确定。

直线与x轴的截距为a，与y轴的截距为b，则直线的截距式方程为：$$\\frac{x}{a} + \\frac{y}{b} = 1$$3. 一般式方程直线的一般式方程表示为Ax+By+C=0，其中A、B、C为常数，且A和B不同时为零。

4. 法线斜截式方程与直线的点斜式方程对应的法线斜截式方程为：$$y-y_1=-\\frac{1}{k}(x-x_1)$$圆的方程公式1. 标准方程圆的标准方程由圆心(ℎ,k)和半径r确定。

圆的标准方程为：(x−ℎ)2+(y−k)2=r22. 一般方程圆的一般方程表示为x2+y2+Dx+Ey+F=0，其中D、E、F为常数。

3. 截距方程如果圆与x轴和y轴分别有截距a和b，则圆的截距方程为：$$\\frac{x^2}{a^2} + \\frac{y^2}{b^2} = 1$$4. 参数方程圆的参数方程方程由圆心(ℎ,k)和半径r确定。

设角度 $\\theta$ 是圆心与某点(x,y)所在的连接线与x轴正半轴的夹角，则点(x,y)的参数方程为：$$x = h + r \\cos \\theta$$$$y = k + r \\sin \\theta$$5. 圆的直径方程若圆的两个端点分别为A(x1,y1)和B(x2,y2)，则圆的直径方程为：(x−x1)(x−x2)+(y−y1)(y−y2)=0结论本文介绍了直线与圆的方程公式大全，包括直线的点斜式方程、截距式方程、一般式方程和法线斜截式方程，以及圆的标准方程、一般方程、截距方程、参数方程和直径方程。

与圆相交直线弦长公式
与圆相交的直线弦长公式可以通过以下步骤推导：
1.设圆的方程为x2+y2=r2，其中r是圆的半径。

2.设直线的方程为y=kx+b，其中k是直线的斜率，b是直线的截
距。

3.联立圆的方程和直线的方程，得到关于x的二次方
程(k2+1)x2+2kbx+b2−r2=0。

4.由于直线与圆相交，所以二次方程有两个实根，分别对应直线
与圆的两个交点的x坐标。

设这两个实根为x1和x2，则根据韦达定理，有x1+x2=−k2+12kb和x1×x2=k2+1b2−r2。

5.弦长公式可以通过计算两个交点之间的距离得到。

由于交点在
直线上，所以弦长L可以表示为L=1+k2×∣x1−x2∣。

6.将x1+x2和x1×x2代入弦长公式，得到L=1+k2×(x1+x2)2−4x1×x2。

7.进一步化简，得到L=1+k2×(−k2+12kb)2−4×k2+1b2−r2。

8.最终化简得到L=∣k2+1∣2r1+k2r2−b2。

这就是与圆相交的直线弦长公式。

其中，r是圆的半径，k是直线的斜率，b是直线的截距。

需要注意的是，这个公式只适用于直线与圆相交的情况，如果直线与圆相切或完全在圆内，则需要使用其他方法计算弦长。

直线与圆的极坐标方程公式在数学中，直线和圆是非常常见的几何图形。

通过极坐标系，我们可以更加简洁地表示直线和圆的方程，使得问题的解析更加方便和直观。

本文将介绍直线和圆在极坐标系下的方程公式。

直线的极坐标方程在极坐标系下，直线的方程通常被表示为极坐标参数等于常数的形式。

一个通用的直线方程为：r = p·cos(θ − α)其中，r 表示极坐标径向距离，p 表示直线到原点的距离，θ 表示角度，α 表示直线的偏转角度。

具体地，当直线与极坐标系的x 轴的交点不在原点时，直线的方程可以表示为：r = p·cos(θ − α) + d·sin(θ − α)·cot(α)其中，d 表示直线与极坐标系的 x 轴的交点到原点的距离。

圆的极坐标方程在极坐标系下，圆的方程可以表示为极坐标径向距离等于常数的形式。

一个通用的圆方程为：r = a + b·sin(θ − α)其中，r 表示极坐标径向距离，a 表示圆心到极坐标系的 x 轴的交点的距离，b表示圆的半径，θ 表示角度，α 表示圆的旋转角度。

需要注意的是，当圆心位于极坐标系的 x 轴上时，圆的方程可以简化为：r = a + b·sin(θ)应用示例现在我们来看一些直线和圆的极坐标方程的应用示例。

直线的极坐标方程应用示例：假设我们现在有一条直线，该直线与极坐标系的x 轴的交点到原点的距离为4，直线的方向与极坐标系的 x 轴的正方向呈45度角。

那么，直线的极坐标方程可以表示为：r = 4·cos(θ − 45°) + 4·sin(θ − 45°)·cot(45°)圆的极坐标方程应用示例：假设我们现在有一个圆，该圆的圆心到极坐标系的 x 轴的交点的距离为3，圆的半径为2，圆的旋转角度为30度。

那么，圆的极坐标方程可以表示为：r = 3 + 2·sin(θ − 30°)通过这些示例，我们可以更好地理解直线和圆在极坐标系下的方程公式的应用。

高中数学之直线与圆的方程一、概念理解：1、倾斜角：①找α：直线向上方向、x 轴正方向； ②平行：α=0°；③范围：0°≤α＜180° 。

2、斜率：①找k ：k=tan α （α≠90°）； ②垂直：斜率k 不存在； ③范围： 斜率 k ∈ R 。

3、斜率与坐标：12122121tan x x y y x x y y k --=--==α①构造直角三角形（数形结合）； ②斜率k 值于两点先后顺序无关； ③注意下标的位置对应。

4、直线与直线的位置关系：222111:,:b x k y l b x k y l +=+= ①相交：斜率21k k ≠（前提是斜率都存在）特例----垂直时：<1> 0211=⊥k k x l 不存在，则轴，即； <2> 斜率都存在时：121-=•k k 。

②平行：<1> 斜率都存在时：2121,b b k k ≠=； <2> 斜率都不存在时：两直线都与x 轴垂直。

③重合： 斜率都存在时：2121,b b k k ==； 二、方程与公式： 1、直线的五个方程：①点斜式：)(00x x k y y -=- 将已知点k y x 与斜率),(00直接带入即可； ②斜截式：b kx y += 将已知截距k b 与斜率),0(直接带入即可；③两点式：),(2121121121y y x x x x x x y y y y ≠≠--=--其中， 将已知两点),(),,(2211y x y x 直接带入即可；④截距式：1=+bya x 将已知截距坐标),0(),0,(b a 直接带入即可； ⑤一般式：0=++C By Ax ，其中A 、B 不同时为0 用得比较多的是点斜式、斜截式与一般式。

2、求两条直线的交点坐标：直接将两直线方程联立，解方程组即可3、距离公式：①两点间距离：22122121)()(y y x x P P -+-= ②点到直线距离：2200BA C By Ax d +++=③平行直线间距离：2221BA C C d +-=4、中点、三分点坐标公式：已知两点),(),,(2211y x B y x A①AB 中点),(00y x ：)2,2(2121y y x x ++ ②AB 三分点),(),,(2211t s t s ：)32,32(2121y y x x ++ 靠近A 的三分点坐标 )32,32(2121y y x x ++ 靠近B 的三分点坐标 中点坐标公式，在求对称点、第四章圆与方程中，经常用到。

一、必备公高考必备公式、结论、方法、细节五：直线方程与圆的方程式1．斜率公式(1)若直线l 的倾斜角α≠90°，则斜率k ＝tan α.(2)P 1(x 1，y 1)，P 2(x 2，y 2)在直线l 上，且x 1≠x 2，则l 的斜率k ＝y 2－y 1x 2－x 1.2．直线方程的五种形式名称方程适用范围点斜式y －y 0＝k (x －x 0)不含直线x ＝x 0斜截式y ＝kx ＋b 不含垂直于x 轴的直线两点式y －y 1y 2－y 1＝x －x 1x 2－x 1不含直线x ＝x 1(x 1≠x 2)和直线y ＝y 1(y 1≠y 2)截距式x a ＋y b ＝1不含垂直于坐标轴和过原点的直线一般式Ax ＋By ＋C ＝0(A 2＋B 2≠0)平面直角坐标系内的直线都适用3．几种距离公式(1)两点P 1(x 1，y 1)，P 2(x 2，y 2)之间的距离：|P 1P 2|＝(x 2－x 1)2＋(y 2－y 1)2.(2)点P 0(x 0，y 0)到直线l ：Ax ＋By ＋C ＝0的距离：d ＝|Ax 0＋By 0＋C |A 2＋B 2.(3)两条平行线Ax ＋By ＋C 1＝0与Ax ＋By ＋C 2＝0(其中C 1≠C 2)间的距离：d ＝|C 1－C 2|A 2＋B 2.4．圆的标准方程：(x －a )2＋(y －b )2＝r 2(r >0)，其中(a ，b )为圆心，r 为半径．5．圆的一般方程：x 2＋y 2＋Dx ＋Ey ＋F ＝0该方程表示圆的充要条件是D 2＋E 2－4F >0，其中圆心为－D 2，－r ＝D 2＋E 2－4F 2.6．判断直线与圆的位置关系常用的两种方法(1)几何法：利用圆心到直线的距离d 和圆半径r 的大小关系：d <r ⇔相交；d ＝r ⇔相切；d >r ⇔相离．(2)代数法：利用判别式Δ＝b 2－4ac 进行判断：Δ>0⇔相交；Δ＝0⇔相切；Δ<0⇔相离．7．圆与圆的位置关系：设圆O 1：(x －a 1)2＋(y －b 1)2＝r 21(r 1>0)，圆O 2：(x －a 2)2＋(y －b 2)2＝r 22(r 2>0).则：d >r 1＋r 2⇔外离；d ＝r 1＋r 2⇔外切；|r 1－r 2|<d <r 1＋r 2⇔相交；d ＝|r 1－r 2|⇔内切；0≤d <|r 1－r 2|⇔内含二、必备结论1．斜率与倾斜角的关系：由正切图象可以看出：①当α∈0k ∈[0，＋∞)且随着α增大而增大；②当α＝π2时，斜率不存在，但直线存在；③当αk ∈(－∞，0)且随着α增大而增大．2．两条直线的位置关系(1)斜截式判断法：①两条直线平行：对于两条不重合的直线l 1、l 2：(ⅰ)若其斜率分别为k 1、k 2，则有l 1∥l 2⇔k 1＝k 2.(ⅱ)当直线l 1、l 2不重合且斜率都不存在时，l 1∥l 2.②两条直线垂直：(ⅰ)如果两条直线l 1、l 2的斜率存在，设为k 1、k 2，则有l 1⊥l 2⇔k 1·k 2＝－1.(ⅱ)当其中一条直线的斜率不存在，而另一条的斜率为0时，l 1⊥l 2.(2)一般式判断法：设两直线A 1x ＋B 1y ＋C 1＝0与A 2x ＋B 2y ＋C 2＝0，则有：①l 1∥l 2⇔A 1B 2＝A 2B 1且A 1C 2≠A 2C 1；②l 1⊥l 2⇔A 1A 2＋B 1B 2＝0.3．直线系方程：(1)平行线系：与直线Ax ＋By ＋C ＝0平行的直线方程可设为：Ax ＋By ＋m ＝0(m ≠C )；(2)垂直线系：与直线Ax ＋By ＋C ＝0垂直的直线方程可设为：Bx －Ay ＋n ＝0；(3)交点线系：过A 1x ＋B 1y ＋C 1＝0与A 2x ＋B 2y ＋C 2＝0的交点的直线可设：A 1x ＋B 1y ＋C 1＋λ(A 2x ＋B 2y ＋C 2)＝0.4．点与圆的位置关系圆的标准方程(x －a )2＋(y －b )2＝r 2，一般方程x 2＋y 2＋Dx ＋Ey ＋F ＝0，点M (x 0，y 0)，则有：(1)点在圆上：(x 0－a )2＋(y 0－b )2＝r 2，x 02＋y 02＋Dx 0＋E y 0＋F ＝0；(2)点在圆外：(x 0－a )2＋(y 0－b )2>r 2，x 02＋y 02＋Dx 0＋E y 0＋F ＞0；(3)点在圆内：(x 0－a )2＋(y 0－b )2<r 2，x 02＋y 02＋Dx 0＋E y 0＋F ＜0.5．圆的切线方程常用结论(1)过圆x 2＋y 2＝r 2上一点P (x 0，y 0)的圆的切线方程为：x 0x ＋y 0y ＝r 2.(2)过圆(x －a )2＋(y －b )2＝r 2上一点P (x 0，y 0)的圆的切线方程为：(x 0－a )(x －a )＋(y 0－b )(y －b )＝r 2.(3)过圆C ：x 2＋y 2＋Dx ＋Ey ＋F ＝0外一点M (x 0，y 0)作圆的两条切线，则两切点所在直线方程的求法：①以M 为圆心，切线长为半径求圆M 的方程；②用圆M 的方程减去圆C 的方程即得；6．圆与圆的位置关系的常用结论(1)两圆的位置与公切线的条数：①内含：0条；②内切：1条；③相交：2条；④外切：3条；⑤外离：4条．(2)公共弦直线：当两圆相交时，两圆方程(x 2，y 2项系数相同)相减便可得公共弦所在直线的方程．7．常用口诀：①直线带参，必过定点；②弦长问题，用勾股.三、必备方法1．直线的对称问题：(1)点关于线对称：方程组法，设对称后点的坐标为(x，y)，根据中点坐标及垂直斜率列方程组；(2)线关于线对称：①求交点；②已知直线上取一个特殊点，并求其关于直线的对称点；③两点定线即可.(3)圆关于线对称：圆心对称，半径不变.2．直线与圆的相关问题：(1)切线问题：一般设直线点斜式(讨论斜率存在)，然后依据d＝r列方程求解；(2)弦长问题：用勾股，即圆的半径为r，弦心距为d，弦长为l，则根据勾股得＝r2－d2；3．轨迹求法：①直译法：直接根据题目提供的动点条件，直接列出方程，化简可得；②几何法：根据动点满足的几何特征，判断其轨迹类型，然后根据轨迹定义直接写出方程．③代入法：找到要求点与已知点的关系，代入已知点满足的关系式等．四、必备细节1．任何直线都存在倾斜角，但并不是任意直线都存在斜率．2．与直线方程的适用条件、截距、斜率有关问题的注意点：(1)运用点斜式、斜截式方程时：要注意讨论斜率存在性；(2)运用截距式方程时：要注意讨论是否经过原点(过原点的直线x，y轴截距均为0)．注意：截距不是距离，距离是非负值，而截距可正可负，可为零．3．点到直线与两平行线间的距离的使用条件：(1)求点到直线的距离时，应：先化直线方程为一般式．(2)求两平行线之间的距离时，应：先将方程化为一般式且x，y的系数对应相等．4．过一点求圆切线要注意：(1)过圆上一点作圆的切线有且只有一条；(2)过圆外一点作圆的切线有且只有两条，若仅求得一条，除了考虑运算过程是否正确外，还要考虑斜率不存在的情况，以防漏解．。

直线与圆的方程公式职高在职高数学课程中，直线与圆的方程公式是一项重要的内容，掌握了这些公式，可以帮助我们解决与直线和圆相关的各种问题。

本文将介绍直线与圆的方程公式，帮助大家加深对这些知识的理解。

直线的方程公式直线是几何中最基本的图形之一，描述直线的方程公式有多种形式。

其中，我们常用的有斜截式、点斜式和截距式等。

1. 斜截式方程公式斜截式方程公式描述了一条直线的斜率和截距之间的关系。

假设直线的斜率为k，截距为b，则斜截式方程公式可以表示为：y = kx + b斜截式方程公式方便我们根据直线的斜率和截距画出直线，并且可以轻松计算出直线与坐标轴的交点等重要信息。

2. 点斜式方程公式点斜式方程公式描述了一条直线上的已知点和斜率之间的关系。

假设直线上一点的坐标为(x₁, y₁)，直线的斜率为k，则点斜式方程公式可以表示为：y - y₁ = k(x - x₁)点斜式方程公式对于已知一点和斜率的情况下，可以方便地求出直线的方程。

3. 截距式方程公式截距式方程公式描述了一条直线与x轴和y轴的截距之间的关系。

假设直线与x轴的截距为a，与y轴的截距为b，则截距式方程公式可以表示为：x/a + y/b = 1截距式方程公式适用于已知直线与x轴和y轴的截距的情况下，可以方便地求出直线的方程。

圆的方程公式圆是一个几何图形，由一组到圆心的等距离点组成。

描述圆的方程公式同样有多种形式，在职高数学中，我们常用的有标准方程和一般方程。

1. 标准方程公式标准方程公式描述了圆的圆心和半径之间的关系。

假设圆的圆心坐标为(h, k)，半径为r，则标准方程公式可以表示为：(x - h)² + (y - k)² = r²标准方程公式方便我们根据圆心和半径画出圆，并且可以轻松计算出圆的周长、面积等重要信息。

2. 一般方程公式一般方程公式描述了圆的一般性质，不直接给出圆的圆心和半径。

假设圆的一般方程为：x² + y² + Dx + Ey + F = 0一般方程公式适用于已知圆的一些性质，例如与已知直线的关系或与其他几何图形的关系等。

直线与圆的方程知识点总结
直线与圆的方程是解析几何中的基本知识点，下面是关于直线与圆的方程的一些重要知识点总结：
直线方程知识点总结：
1. 直线的点斜式方程：y-y0=k(x-x0)，其中 (x0, y0) 为直线上的一点，k 为直线的斜率。

2. 直线的斜截式方程：y=kx+b，其中 k 为直线的斜率，b 为 y 轴上的截距。

3. 直线的两点式方程：(y-y1)/(y2-y1)=(x-x1)/(x2-x1)，其中 (x1, y1) 和
(x2, y2) 为直线上的两点。

4. 直线的截距式方程：x/a + y/b = 1，其中 a 和 b 分别为直线在 x 轴和 y 轴上的截距。

5. 直线的一般式方程：Ax + By + C = 0，其中 A、B、C 为常数，且 A 和
B 不为 0。

圆的方程知识点总结：
1. 圆的标准式方程：(x-h)^2 + (y-k)^2 = r^2，其中 (h, k) 为圆心坐标，r 为半径。

2. 圆的参数式方程：x=h+rcosθ, y=k+rsinθ，其中 (h, k) 为圆心坐标，r 为半径，θ 为参数。

3. 圆的极坐标式方程：ρ=r，其中 r 为半径，θ 为极角。

4. 圆的直径式方程：x^2 + y^2 + Dx + Ey + F = 0，其中 D、E、F 为常数。

5. 圆的一般式方程：x^2 + y^2 + Ax + By + C = 0，其中 A、B、C 为常数。

在直线与圆的方程中，还有一些重要的知识点和概念，如直线的法线式和参数式，圆的切线和割线等。

理解和掌握这些概念和公式对于解决几何问题非常重要。