人工智能 约束满足问题 6-3 回溯搜索CSP

约束满足问题及其求解方法研究随着现代科技的快速发展，人们对各种求解问题的需求日益增长，其中，约束满足问题是一个相对独特却又十分重要的问题类型。

在此，我们将从定义、特点、应用以及求解方法几个方面谈一谈约束满足问题及其求解方法的相关内容。

一、定义约束满足问题（Constraint Satisfaction Problem，CSP）是指在一定约束条件下，满足对变量的限制（约束条件）的数学问题。

因此，CSP可以被定义为一个元组（X,D,C）：X 表示所有的变量集合，D 表示每个变量 x ∈ X 的定义域，C 表示x∈X 的约束集合。

二、特点CSP问题通常具有以下几个特点：1、通用性强：CSP问题可以用于描述各种类型的问题，如图着色和行程问题等。

2、规模大：CSP问题通常涉及到大量的变量和约束，其求解过程相对复杂，因此，系统的设计和求解方法是至关重要的。

3、复杂度高：大多数CSP问题属于NP完全问题，无法在多项式时间内精确地解决，同时，这些问题的求解方法也比较困难。

三、应用CSP的应用非常广泛，以下是其中几个代表性的应用领域。

1、人工智能：CSP可以用于优化问题、机器学习、计算机视觉等人工智能任务。

2、排程问题：CSP可以用于作业坊调度、员工排班等任务中。

3、生产问题：CSP可以用于零件生产、工厂排布等任务中。

4、电子设计自动化：CSP可以用于电路自动布局、芯片设计等任务中。

四、求解方法针对CSP问题的复杂性，目前有多种求解方法，这里简要介绍几种主流的方法。

1、基于启发式算法的方法：启发式算法通常针对CSP问题中的子问题进行求解，能够得到比较好的求解结果，但是求解时间可能较长。

2、基于局部搜索的方法：局部搜索算法的优点在于其求解速度较快，但其无法得到全局最优解，可能只能得到局部最优解。

3、基于约束传播的方法：约束传播算法利用限制传播的策略进行求解，能够得到可行解或确定无解，但是在求解大规模问题方面表现相对不足。

csp约束的表达方式约束满足问题（ConstraintSatisfactionProblem，CSP）是一种表示限制和解决的方法，它被广泛用于智能系统中。

那么，CSP有哪些不同的表达方式呢？第一种CSP表达方式就是采用数学公式表示，它是由一些变量和约束条件组成的。

比如，x+y=z是一个约束条件，该约束条件表明变量x、y、z之间存在某种关系。

它可以用于布尔表达式中，比如可以用来表示x>y且z< w的关系。

第二种CSP表达方式就是采用属性-值表示法，这种表达方式在实现上更加方便。

其中，属性代表变量的多个特征，而值列表则代表变量可能的取值范围。

比如变量age的属性有年龄，其值则可以是1到100；变量sex的属性有性别，其值则可以是男或女两种。

这种表达方式可以用来表示变量之间的关系，比如age>50，sex=“男”。

第三种CSP表达方式便是采用搜索树表示，它可以用来表示复杂的约束关系，比如一个搜索树可以表示age>50且sex=“男”的约束关系。

搜索树可以分解为若干个细小的步骤，每一步均可以采用不同的策略来进行搜索。

第四种CSP表达方式是采用“约束网”，也可以称之为“约束图”。

约束网是一种广泛使用的CSP模型，可以用来表达复杂的约束关系，它由一系列结点和边组成，结点表示变量，而边表示约束条件。

约束网可以用来表示变量之间的关系，比如a=b且b≤c且c>d的约束关系。

最后，CSP还有另一种表达方式，即采用“规则”的方式表达。

规则的形式可以是if-then结构，也可以是case-based结构。

规则通常包括变量和其可能取值，以及变量之间的约束关系。

比如if age>50 then sex=“男”，if sex=“男” then age>50，case age: 1-10-->“少年”，11-20-->“青年”，21-50-->“中年”，51-99-->“老年”。

第五章约束满足问题教学内容：本章我们将看到不把状态仅仅当作小黑盒子，如何能引导设计出更强有力的新搜索方法，以及对问题的结构和复杂性有更深的理解教学重点：1•约束满足问题的定义。

2•搜索算法求解大型问题。

3•问题分解的办法。

教学难点：1 •约束满足问题2. CSP的回溯搜索和局部搜索5.1约束满足问题约束满足问题，简称CSP。

由一个变量集合Xi和一个约束集合Ci定义的, 每个约束Ci包括一些变量的子集，这些子集的值之间允许合并。

CSP问题中的状态表示是符合一个标准模式的，后继函数和目标测试能够以适用于所有CSP的普遍方式写出。

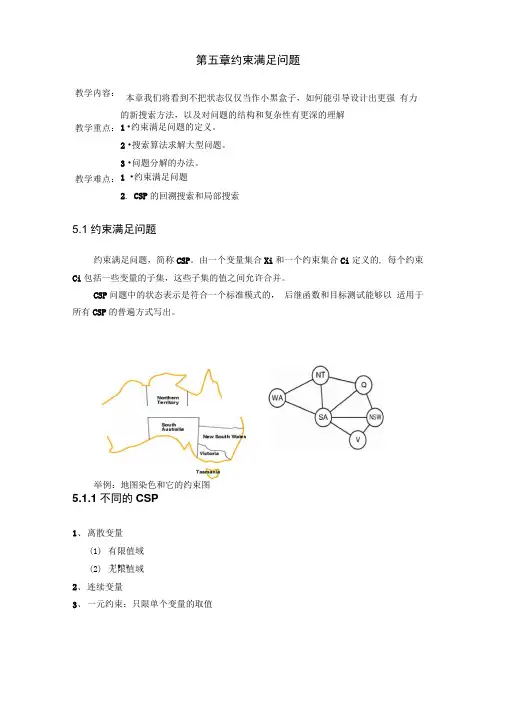
举例：地图染色和它的约束图5.1.1不同的CSP1、离散变量(1)有限值域AT曲1也(2)无限值域2、连续变量3、一元约束：只限单个变量的取值4、二元约束：与两个变量有关5、高阶约束：涉及三个或更多的变量举例：一个密码算术游戏T W 0 -h T WQ FOUR5.1.2现实世界的CSP（1）分配问题（2）时间表问题（3）交通调度（4）工厂调度5.1.3标准搜索表述CSP问题可以向标准搜索问题一样给出如下的增量形式化:（1）初始状态：空的赋值（2）后继函数：给任何未赋值的变量赋一个值（3）目标测试：检查当前的赋值是否完全5.2 CSP的回溯搜索CSP搜索算法生成后继时，在搜索树的每个节点上只考虑单个变量的可能赋值。

提出问题：（1）下一个该给哪个变量赋值？（2）当前变量赋值对其他未赋值的变量意味着什么？（3）可否避免重复失败？最少约束值：优先选择的值是在约束图中排除邻居变量的可选知最少的5.2.1 前向检验概念：（1）记录那些未赋值的变量的变量值（2）当任何的变量没有合法取值的时候停止搜索举例：用前向检验方法解决地图染色搜索的进程。

5.2.2约束传播虽然前向检验能检验出许多矛盾，它还是不能检验出所有的矛盾。

约束传播一一将一个变量的约束内容传播到其他变量上的一般术语。

弧相容：（1）该思想提供了一个实际比前向检查更强的约束传播的快速方法。

人工智能原理_北京大学中国大学mooc课后章节答案期末考试题库2023年1.Turing Test is designed to provide what kind of satisfactory operationaldefinition?图灵测试旨在给予哪一种令人满意的操作定义？答案:machine intelligence 机器智能2.Thinking the differences between agent functions and agent programs, selectcorrect statements from following ones.考虑智能体函数与智能体程序的差异，从下列陈述中选择正确的答案。

答案:An agent program implements an agent function.一个智能体程序实现一个智能体函数。

3.There are two main kinds of formulation for 8-queens problem. Which of thefollowing one is the formulation that starts with all 8 queens on the boardand moves them around?有两种8皇后问题的形式化方式。

“初始时8个皇后都放在棋盘上，然后再进行移动”属于哪一种形式化方式？答案:Complete-state formulation 全态形式化4.What kind of knowledge will be used to describe how a problem is solved?哪种知识可用于描述如何求解问题？答案:Procedural knowledge 过程性知识5.Which of the following is used to discover general facts from trainingexamples?下列中哪个用于训练样本中发现一般的事实？答案:Inductive learning 归纳学习6.Which statement best describes the task of “classification” in machinelearning?哪一个是机器学习中“分类”任务的正确描述？答案:To assign a category to each item. 为每个项目分配一个类别。

csp问题的约束传播方法约束传播（Constraint Propagation）是一种以计算机技术解决问题和解决约束满足问题的方法，是强制约束满足问题的重要工具之一。

约束传播技术的目的是通过分析与它所围绕的约束组有关的信息，以减少可能的候选项，使得可用的解决方案变得显而易见。

在 CSP 问题中，它可以根据各种特定的约束条件，对所有可能的解决方案作出估计、删减和调整，直至求出最优解。

约束传播方法主要实现了三种机制：约束网络检查（Consistency Checking），测试和修复（Search & Repair）以及变换（Transformation）。

约束网络检查是一种从值域约束网络中检索符合约束条件的变量值的方法。

它将从抽象语言描述的约束网络中获取约束信息，并通过对约束网络上在每个变量上的值的检查，确定它们是否满足所有的约束条件。

约束网络检查也是一种实现贪心搜索的方法，它会将符合约束条件的值保留以便随后利用。

测试和修复是在约束网络检查过程中引入一种新的方法，即从满足约束条件的候选变量值中确定最优解的方法，它既可以在约束网络检查的基础上进行，也可以单独使用。

在测试和修复的过程中，CSP的求解者枚举变量值的所有可能组合，然后检查这些组合是否满足所有的约束条件。

如果不满足，就尝试修改其中的一个变量，以使其满足约束条件，通过进行变量的枚举和检验，来寻找满足约束条件的最优解。

最后，变换可以被用来删减或变换原始的约束网络，以获得更加有效的求解过程。

变换过程中可以将原始约束网络中的一些变量值替换成舍入（Roundoff）值或其他值，从而减少原有的候选变量值，使求解过程变得更加有效，从而降低求解的时间和资源消耗。

总的来说，约束传播在 CSP 问题中的应用可以使得求解效率更高，从而更快地得出最优解。

机器智能-⾼频问题：CSP搜索CSP搜索的作⽤就是在应⽤约束传播缩⼩值域范围后开始使⽤搜索算法来得到最终结果。

⾸先来看⼀下通⽤搜索模式：输⼊是⼀个CSP问题，输出是⼀个解决⽅案。

a、转态是由赋值的变量决定的b、初始状态设为空{}c、步骤：给⼀个没有赋值的变量赋值，该赋值不与当前已赋值的变量相冲突d、⽬标测试：如果所有的赋值完成且满⾜终⽌状态，则搜搜结束e、CSP适⽤于通⽤的搜索模式，并采⽤深度搜索⽅法f、缺点：重复计算，每⼀层对所有节点赋值进⾏枚举g、变量的赋值顺序是可以交换的h、改进：每⼀层只需要考虑⼀个变量的赋值①、算法之前固定赋值顺序②、可减少到d^ni、对CSP采⽤深度优先的单个变量赋值，当检测到（某个分⽀）不相容时，返回上⼀层赋值（这条路⾛不通，⾛另⼀个）实际上就是就优化过的值域范围中遍历所有的可能性，然后找到满⾜条件的结果。

以上⼀次的问题为例：上次我们得到了，ABC三个变量的值域分别为：{1,2,3}；{0,1,2}；{0,2,4}那么，我们就可以⽤通⽤搜索模式，获得这个问题的CSP搜索树：最初的是这样的：这个并没有画完，还有很多。

可以看出来，很明显有很多的重复的分⽀，⽐⽅说A=1B=0C=0和B=0A=1C=0这样的，所以，很⾃然的就有了改进，即每层只考虑⼀个变量，如第⼀层就考虑A，第⼆层就考虑B，以此类推，得到了下⾯的CSP搜索树：可以看到，⼜改进了很多，减少了很多的分⽀。

但这种⽅法还是有很多的问题，⽐⽅说我为什么第⼀层不能是变量B？，所以就有了提⾼回溯搜索算法的效率的⽅法：①、选择变量赋值的顺序：先A还是先B·最受约束的变量：优先选择最少剩余值的变量进⾏赋值（即当前值域最⼩的变量）；减少回溯的次数。

但这个题⽬中A、B、C的值域都只有三个，所以只能任选⼀个了。

·约束最多的变量：优先选择最能约束其他变量的变量进⾏赋值（即约束条件中提到最多的变量）；减少回溯的次数。

约束满足问题（CSP）的算法探索约束满足问题（Constraint Satisfaction Problem，CSP）是人工智能领域中的一个重要问题类型，涉及到在一组变量上的取值，同时满足一系列约束条件。

CSP在实际生活中有着广泛的应用，比如在排课、时间表安排、资源分配等领域都可以看到CSP的身影。

为了解决CSP问题，人们提出了各种不同的算法，本文将对CSP问题及其相关算法进行探索和介绍。

### 什么是约束满足问题（CSP）？约束满足问题是指一组变量，每个变量有一定的取值范围，同时还有一系列约束条件限制这些变量的取值。

CSP的目标是找到一组取值，使得所有约束条件都得到满足。

通常来说，CSP可以用一个三元组表示：CSP = (X, D, C)，其中：- X = {X1, X2, ..., Xn} 表示一组变量；- D = {D1, D2, ..., Dn} 表示每个变量对应的取值范围；- C = {C1, C2, ..., Cm} 表示约束条件的集合。

### CSP的经典问题CSP问题有许多经典的应用场景，下面介绍几个常见的CSP问题：1. **地图着色问题**：给定一张地图和一定数量的颜色，要求每个地区用一种颜色着色，相邻的地区不能使用相同的颜色。

2. **八皇后问题**：在8×8的国际象棋棋盘上放置8个皇后，使得它们互相不能攻击到对方。

3. **数独问题**：填充一个9×9的网格，使得每一行、每一列和每个3×3的子网格中的数字都是1到9且不重复。

### CSP的求解算法为了解决CSP问题，人们提出了多种求解算法，常见的包括回溯算法、约束传播算法和启发式搜索算法等。

下面分别介绍这几种算法： #### 1. 回溯算法回溯算法是解决CSP问题最常用的方法之一。

其基本思想是逐步尝试每个变量的取值，并检查是否满足约束条件，如果不满足则回溯到上一步重新选择取值。

回溯算法的优点是简单易懂，但在处理大规模问题时效率较低。

The Structure of ProblemsContents☐6.5.1 Decomposing Problem☐6.5.2Independent Sub-problems☐6.5.3 Tree-structured Problems☐6.5.4 Reduce Constraint Graphs to Tree StructuresDecomposing Problem 问题分解☐The structure of problem as represented by constraint graph can be used to find solutions.由约束图所表征的问题结构，可以用于寻找解。

☐The complexity of solving a CSP is strongly related to the structure of its constraint graph.求解一个CSP问题的复杂性，与约束图的结构密切相关。

☐The problem in the real world can be decomposedinto many sub-problems.现实世界的问题可以被分解为许多子问题。

Example:Coloring Tasmania and coloring themainland are independent sub-problems.Divide and Conquer!对塔斯曼尼亚着色与澳洲大陆着色是相互独立的子问题。

Independent Sub-problems独立子问题☐They are identifiable as connected components of constraint graph.独立子问题可被标识为约束图的联接组件。

☐Suppose a graph of n variables can be broken into sub-problems of only c variables:each worst-case solution cost is O((n/c)·d c), linear in n.设n个变量的图可分解为仅有c个变量的子问题：每个最坏解的代价是O((n/c)·d c), n的线性关系。

Constraint Propagation: Inference in CSPsContents☐6.2.1 Overview of Constraint Propagation ☐6.2.2Node Consistency☐6.2.3 Arc Consistency☐6.2.4 Path Consistency☐6.2.5 k-Consistency☐Regular state-space search: 常规的状态空间搜索⏹can do only one thing, search.只能做一件事，搜索。

☐CSPs: 约束满足问题⏹can do search, choose a new variable assignment from several possibilities,能做搜索，从若干可能性中选择一个新的变量赋值，⏹can also do a specific type of inference, called constraint propagation.还能做一种特殊类型的推理，称为约束传播。

☐Constraint Propagation: 约束传播⏹uses the constraints to reduce the number of legal values for a variable, which inturn can reduce the legal values for another variable, and so on.采用约束来减少一个变量的合法值的数量，相应地可以减少其它变量的合法值，以此类推。

☐Those techniques are used to modify a constraint satisfaction problem.这些技术被用于改变一个约束满足问题。

☐More precisely, they enforce a form of local consistency, which are conditions related to the consistency of a group of variables and/or constraints.更精确地说，它们严格实施局部一致性，这种形式是一组变量和约束一致性相关的条件。

基于CSP算法的数独游戏求解技术在当今时代，数独作为一种智力游戏已经越来越受欢迎。

数独游戏的规则非常简单，把1-9这9个数字填入一个9*9的格子里，使得每行、每列和每个3*3的九宫格内都没有重复的数字。

然而，对于初学者来说，解决数独游戏似乎并不是件轻松的事情。

因此，这就需要一种更加科学、高效的方法来解决这个问题。

本文将介绍一种基于CSP算法的数独游戏求解技术。

什么是CSP算法？CSP算法，即约束满足问题算法，是解决一类复杂的计算问题的有效方法。

CSP算法的核心思想是对问题进行明确的建模，并将解决问题的计算过程转化为一种带有约束的搜索过程。

它能够很好地解决排列、组合和最优化问题等。

并且，由于此算法能够有效地简化问题所需的计算量，因此具有广泛的应用前景。

数独游戏的建模在数独游戏中，我们需要填数到每一个格子，并且保证每行、每列和每个3*3的九宫格内都没有重复的数字。

因为每个格子只有一些特定的数字可以被填入，所以我们可以将这个问题转化为一个经典的约束满足问题。

首先，我们定义一个变量用来表示每个格子的状态，该变量可以取1~9这9个数字中的一个。

然后，对于数独游戏中的每一行、每一列和每个3*3九宫格，我们定义一个约束函数，该函数用于保证该行、该列或该九宫格中的数字不重复。

接下来，我们需要将整个问题建模为CSP问题。

具体来说，我们需要满足以下三个条件：1.定义变量和变量的取值范围对于每个格子，我们定义一个变量，该变量取值范围为1~9。

2.定义约束函数对于数独游戏中每一行、每一列和每个3*3九宫格，我们定义一个约束函数。

该约束函数用于保证该行、该列或该九宫格中数字不重复。

3.定义约束满足问题对于整个数独游戏，我们将变量和约束函数结合起来，构成一个约束满足问题。

我们需要寻找满足所有约束条件的解。

基于CSP算法的数独游戏求解技术有了上面的建模，我们就可以使用CSP算法来求解数独游戏了。

基于CSP算法的数独游戏求解技术具有如下优点：1.高效性该算法能够有效地简化问题所需的计算量，从而大大提高计算效率。