压水反应堆的热功率

小型核电反应堆的现状及未来发展1 核电反应堆堆型现状核能发电始于20世纪50年代，出于追求核电运行规模经济性的需要，核电机组的设计趋向于大型化，在70年代，核电机组的平均容量达到大约1000 MWe，发电用核反应堆的容量从60 MWe发展到超过1300 MWe。

目前，美国拥有104台现役核电反应堆，总容量约99210 MWe，平均每台容量为953 MWe；法国共有59台运行反应堆机组，总容量63363 MWe，平均每台容量为1074 MWe；日本拥有54台核电机组，总容量约为45468 MWe，平均每台容量为842 MWe。

这些国家拥有庞大而相对完善的电网，能承受单次1000 MWe或1300 MWe负荷的变化。

第3代核电站采用的堆型除了AP600以外也是大型机组，如1300 MW级的System 80+和ABWR，1000 MW级的AP1000 和VVER-1000，1500 MW级的EPR等。

近年来，韩国、中国等国家的核电得到了很大发展，这些国家引进或自主开发、建设的核电站基本上也是大型机组。

21世纪80～90年代，工业化国家的发电容量日趋饱和，电网开始出现容量过剩的问题，电网对大容量机组的并入显得越来越不适应，电力公司也不允许一台大型机组长时间地做低功率调峰运行， 因为这样会给经济性带来严重影响。

因此，近年来人们对中、小型反应堆(SMR)又产生了兴趣，希望这些中小型反应堆能更好地适应工业国家的电力负荷需求，以及满足那些电网不能承受大容量机组并入的发展中国家的电力需求。

1.1 小型核电反应堆的状况国际原子能机构(IAEA)将“小型”机组定义为300MWe以下的机组，而电功率在300MWe以上、600MWe以下的为中型反应堆机组。

中、小型反应堆所涉及的技术是多样化的，反应堆类型有：轻水堆、高温气冷堆、液态金属反应堆和熔盐堆，而当前最主要的2种技术均利用高温氦气直接驱动涡(气)轮机。

目前开发程度较为先进的中、小型反应堆有如下一些：美国国会现在正在筹集资金研究小型模块式核电厂和先进气冷堆设计(也是模块化，10个或更多模块机组逐步建成一个大电厂)。

压水堆核电站出力提升常规岛汽水系统可靠性分析报告摘要：核电站设计额定负荷通常是一个较为保守的定值，本文主要根据常规岛汽水回路的主要系统关键参数论证百万级压水堆核电站最大出力提升至1180MWe的可行性。

主要从常规岛汽水回路的主要系统关键参数进行分析。

主要分析了凝结水系统，主给水系统，蒸汽旁路排放系统，汽水分离再热系统等参数变化前后是否仍然在设计范围内。

最后论证提升至1180MW是可行的。

关键字：出力提升常规岛承载能力可靠性1.概述1.1目的提示核电站的额定功率，在核电站系统可接受的情况下有利于提示核电站的年度发电量，有较一定的经济效应。

2.定义/缩写T-MCR工况：最大连续运行工况SCR工况：夏季出力工况VWO工况：汽机进汽调阀全开工况3.机组运行数据分析3.1T-MCR工况下机组实际参数根据某核电机组（A机组）商运至今实际运行参数及设计参数进行分析，选取（A机组）T-MCR工况下机组运行参数与设计值对比相关参数如表1：表1：某核电机组T-MCR工况下机组运行参数与设计值对比表通过对上述数据分析，发现该机组在冬季由于海水气温减低，机组背压相对低于设计值，反应堆功率热功率在此情况下仍有25.27-37.27MWe 的预量，因此提升机组出力具有一定的可行性。

3.2机组出力提升至边界值预测参数根据前期研究可知，核电机组由停机工况升功率到最大出力工况时，主蒸汽流量、主给水流量、凝结水流量等二回路汽水参数变化趋势均随电功率、核功率增加而线性增加，电功率、核功率稳定于某一点时，蒸汽流量、主给水流量、凝结水流量均稳定在一点波动运行，依据该现象可根据电动率、核功率边界限值预测出机组处力提升值目标值时主蒸汽流量、主给水流量、凝结水流量对应的参数。

1）核功率线性变化预测参数根据某核电机组（A机组）2月机组启动参数拟合生成曲线图：A机组核功率与电功率、主蒸汽流量、主给水流量、凝结水流量的曲线走势图。

通过生成曲线趋势分析，预测A机组核功率提升至边界值3060 MWe时，相对应的主蒸汽流量、主给水流量、凝结水流量分别为1710.971kg/s、1731.691kg/s、1093.16 kg/s。

6.2 AP-600，西屋西屋公司先进的非能动压水堆AP-600是一种电功率为600MW的压水反应堆，它具有先进的非能动的安全特性，并且通过广泛采用简化设计从而显著提高了电站的建造，运行和维护性能。

电站设计充分利用了经过30多年压水堆运行经验验证的成熟技术。

在世界范围内，压水堆的比重占所有轻水反应堆的76%，而67%的压水堆是建立在西屋压水堆技术基础之上的。

AP-600的设计目标是达到很高的安全和性能记录。

它的设计虽然基于保守的已被验证的压水堆技术，但是在安全特性方面强调依赖自然力。

安全系统尽可能使用自然驱动力比如压缩气体，重力流和自然循环流动。

安全系统不使用能动部件（比如泵，风机或柴油发电机）并且设计为功能实现不需要安全级的支持系统（比如交流电源，部件冷却水，生活服务水，采暖通风）。

控制安全系统所需的运行人员的操作在数量上和复杂度上都尽可能小；其宗旨就是用自动实现取代运行人员的操作。

最终结果就是形成的设计显著降低了复杂度并提高的可操作性。

AP-600的标准设计符合所有适用的美国核管会标准。

大量的安全分析工作已经完成，相关内容写入了提交核管会的标准安全分析报告（SSAR）和概率风险评价（PRA）。

广泛的实验计划也已经完成，从而验证了电站的创新性设计在运行中将与预期的设计和分析一致。

概率风险评价（PRA）的结果表明了其具有满足先进反应堆设计目标的非常低的堆芯损坏几率，并且由于改善了安全壳的隔离与冷却能力，其也具有很低的放射性泄漏几率。

AP-600的设计理念中非常重要的一个方面是关注电站的可操作性和可维护性。

这些因素已经融入了其整个的设计过程。

AP-600的设计具有许多独到之处，比如通过简化设计在提高可操作性的同时也减少了部件及其配套设施的数量。

特别是，简化的安全系统显著地简化了技术规格，从而降低了监督的要求。

通过强调已验证的部件的应用，从而确保达到高水平的可靠性同时具有很低的维护要求。

部件的标准化降低了备件的数量，减小了维护的培训要求，并且使维护周期进一步缩短。

第一章核反应堆是一个能维持和控制核裂变链式反应，从而实现核能到热能转换的装置。

传热机理—热传导、热对流、热辐射世界上第一座反应堆是1942 年美国芝加哥大学建成的。

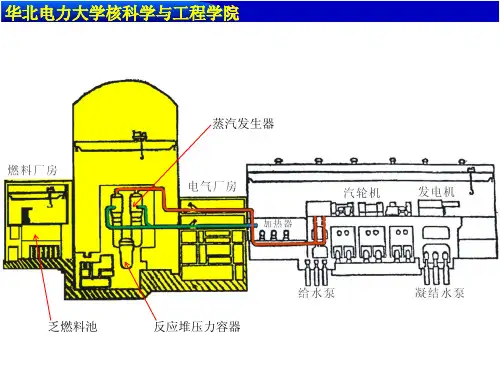
核反应堆按照冷却剂类型分为轻水堆、重水堆、气冷堆、钠冷堆按照用途分为实验堆、生产堆、动力堆按中子能量分类：热中子堆、中能中子堆、快中子堆以压水堆为热源的核电站称为压水堆核电站主要有核岛和常规岛核岛的四大部件为蒸汽发生器、稳压器、主泵、堆芯五种重要堆型压水堆沸水堆重水堆高温气冷堆钠冷快中子增值堆水作为冷却剂慢化剂的优缺点：轻水作为冷却剂缺点是沸点低，优点具有优良热传输性能，且价格便宜。

描述反应堆性能的参数反应堆热功率[MWh]：反应堆堆芯内生产的总热量电厂功率输出[MWe]：电厂生产的净电功率电厂净效率[%]：电厂电功率输出/反应堆热功率容量因子[%]：某时间间隔内生产的总能量/[(电厂额定功率)×该时间间隔]功率密度[MW/m3]：单位体积堆芯所产生的热功率线功率密度[kW/m]：单位长度燃料元件内产生的热功率比功率[kW/kg]：反应堆热功率/可裂变物质初始总装量燃料总装量[kg]：堆芯内燃料总质量燃料富集度[%]：易裂变物质总质量/易裂变物质和可转换物质总质量比燃耗[MWd/t]：堆芯工作期间生产的总能量/可裂变物质总质量本章主要内容1.压水堆的主要特征2 沸水堆和重水堆的主要特征3 热工水力学分析的目的与任务（这个可以忽略）第二章（本章可以覆盖部分计算题）热力学第一定律：热力系内物质的能量可以传递，其形式可以转换，在转换和传递过程中总能量保持不变。

热力学第二定律（永动机不可能制成）：不可能将热从低温物体传至高温物体而不引起其它变化；不可能从单一热源取热，并使之完全转变为有用功而不产生其它影响；不可逆热力过程中的熵的微增量总是大于零。

最基本的状态参数：压力（压强Pa，atm，bar，at）比体积（m3/kg）温度内能：系统内部一切微观粒子的一切运动形式所具有的能量总和，U焓：热力学中表示物质系统一个状态参数–H，数值上等于系统内能加上压强与体积的乘积。

课程设计报告名称：核反应堆热工分析课程设计题目：利用单通道模型进行反应堆稳态热工设计院系：--------------------班级：----------学号：---------学生姓名：-----------指导教师：--------设计周数：--------成绩：日期：2014年6 月25日一、课程设计的目的与要求反应堆热工设计的任务就是要设计一个既安全可靠又经济的堆芯输热系统。

对于反应堆热工设计，尤其是对动力堆，最基本的要求是安全。

要求在整个寿期内能够长期稳定运行，并能适应启动、功率调节和停堆等功率变化，要保证在一般事故工况下堆芯不会遭到破坏，甚至在最严重的工况下，也要保证堆芯的放射性物质不扩散到周围环境中去。

在进行反应堆热工设计之前，首先要了解并确定的前提为：（1）根据所设计堆的用途和特殊要求（如尺寸、重量等的限制）选定堆型，确定所用的核燃料、冷却剂、慢化剂和结构材料等的种类；（2）反应堆的热功率、堆芯功率分布不均匀系数和水铀比允许的变化范围；（3）燃料元件的形状、它在堆芯内的分布方式以及栅距允许变化的范围；（4）二回路对一回路冷却剂热工参数的要求；（5）冷却剂流过堆芯的流程以及堆芯进口处冷却剂流量的分配情况。

在设计反应堆冷却系统时，为了保证反应堆运行安全可靠，针对不同的堆型，预先规定了热工设计必须遵守的要求，这些要求通常就称为堆的热工设计准则。

目前压水动力堆设计中所规定的稳态热工设计准则，一般有以下几点：（1）燃料元件芯块内最高应低于其他相应燃耗下的熔化温度；（2）燃料元件外表面不允许发生沸腾临界；（3）必须保证正常运行工况下燃料元件和堆内构件得到充分冷却；在事故工况下能提供足够的冷却剂以排除堆芯余热；（4）在稳态额定工况和可预计的瞬态运行工况中，不发生流动不稳定性。

在热工设计中，通常是通过平均通道（平均管）可以估算堆芯的总功率，而热通道（热管）则是堆芯中轴向功率最高的通道，通过它确定堆芯功率的上限，热点是堆芯中温度最高的点，代表堆芯热量密度最大的点，通过这个点来确定DNBR。

压水堆燃料棒热力计算与(火用)分析张钧波;张功伟;张敏【摘要】To investigate the exergy loss of fuel rod during converting nuclear energy into thermal energy, the partial differential equations of steady heat transfer of pressurized water reactor fuel rods and the first and second laws of thermodynamics were used. The exergy analysis method was innovatively combined with the numerical calculation of temperature field. The numerical calculation program was compiled to simulate the fuel rods and heat transfer channels and analyze the temperature distribution,the exergy loss distribution and the energy utilization efficiency during converting nuclear energy into heat energy and during coolant heat transfer. The results show that the fuel rod exergy loss is increased with latter decreasing in the axial direction and increased in the radial direction with the maximum exergy loss coefficient of 0.207 at the edge of fuel core. The exergy loss in the convective heat transfer process is mainly related to the heat transfer temperature difference and increased with latter decreasing along the thermal channel with the total exergy loss coefficient of 0.304.%为了研究燃料棒核能转化为热能过程中的(火用)损,采用压水堆燃料棒稳态传热偏微分方程和热力学第一、第二定律,创新性地将(火用)分析方法与燃料棒温度场数值计算相结合,编制数值计算程序对燃料棒及传热通道进行模拟计算,并分析了核能转换为热能以及与冷却剂换热过程中温度分布、(火用)损的分布和能量的利用效率.结果表明:燃料棒(火用)损沿轴向先增大后减小,沿径向不断变大,在燃料芯块边缘处达到最大,(火用)损系数约为0.207;而对流换热过程中(火用)损主要与传热温差有关,(火用)损沿热通道先增大后减小,该过程累积(火用)损系数约为0.304.【期刊名称】《江苏大学学报（自然科学版）》【年(卷),期】2018(039)003【总页数】6页(P273-278)【关键词】压水堆;燃料棒;温度场;数值计算;(火用)分析;(火用)损【作者】张钧波;张功伟;张敏【作者单位】南京师范大学泰州学院,江苏泰州225300;南京理工大学能源与动力工程学院,江苏南京210094;南京理工大学能源与动力工程学院,江苏南京210094【正文语种】中文【中图分类】TL331核反应堆的安全运行是近代核科学研究的重要课题,在保证堆芯释热有效输出的前提下,尽可能提高核能利用率,也是核动力装置热工设计的主要研究方向[1-3].堆芯内燃料棒传热主要包括芯块导热、包壳传热以及包壳外壁面与冷却剂对流换热3部分,目前研究方法大多以热力学第一定律为基础[4-6],通过数值计算方法对燃料组件传热通道进行模拟计算,从而获得燃料棒及外围冷却剂的温度分布或者包壳表面的热流密度[7-10].但对于燃料棒内能量在数量和质量上综合性研究较少,因此不能准确全面地反映用能过程中存在的薄弱环节.文中结合热力学第一、第二定律,在系统能量平衡的基础上,先采用数值法和解析法获得燃料棒温度场,验证模型的准确性,然后通过(火用)分析法计算正常工况下燃料棒传热过程中(火用)损的分布情况,为节能降耗、提高能量利用率提供参考.1 模型验证在压水堆中燃料棒长度L一般为3～4 m,外径为9.5 mm左右,按设计要求将一定数量燃料芯块装入包壳内,燃料棒外围为热通道,冷却剂自下而上流动,进行对流换热.燃料棒轴向截面如图1所示,Ru为芯块半径,Rci为包壳内径,Rcs为包壳外径.图1 燃料棒轴向截面图1.1 控制方程和离散方程对于通用物理变量φ,一般的稳态扩散方程为(1)式中:f(xi)为几何形状因子；Γφ为对应变量φ的扩散系数;Sφ为单位体积中的净源项.根据方程(1),在圆柱坐标系中,燃料棒的稳态导热微分方程为0≤r≤Rcs,-L/2≤z≤L/2,(2)式中:r为圆柱坐标系半径;k为导热系数;∂T/∂r为r方向的温度变化率;∂T/∂z为z方向的温度变化率;qv为热源项.在导热方程中,扩散系数Γ即为热传导系数k,反应堆正常运行工况下的热源项近似为0≤r≤Ru,(3)式中J0为第一类贝赛尔函数.计算时采用非结构化网格,对方程(1)进行离散.在一个控制体P中,有(4)式中:n为控制体P与其他控制体的交界面数;VP为控制体P体积;SP为控制体P的净源项;Di为扩散项,可表示为交界面i上的法向扩散项Dpi和切向扩散项Dsi之和. Di=Γi(φ)ave,i·Ai=Dpi+Dsi,(5)式中:Γi为交界面i上的热扩散系数;Ai为控制体交界面的面积矢量;(φ)ave,i为相邻控制体中心处φ值的平均矢量,其具体求解方法可参考文献[11].(6)式中:φE和φP分别为控制体E和控制体P的通用物理变量;dsi为两控制体的中心距;esi为其中心连线的单位矢量.=(φ)ave,i·esi.(7)将式(7)代入式(6),然后根据式(5),有Dpi=Γi((8)(9)于是完整的离散方程可写成:(10)(11)该离散方程是基于方程(1)推导的,与坐标无关,适用于任何几何形状,具体过程可参阅文献[11].1.2 边界条件由于燃料棒的长径比很大,在数值求解时可简化计算模型,以秦山核电二期工程堆芯燃料棒为研究对象,取燃料棒长度L=30 mm,芯块半径Ru=4.1 mm,包壳内径Rci=4.20 mm,包壳外径Rcs=4.75 mm,芯块导热系数ku=3.1 W·(m·K)-1,气隙导热系数kg=0.33 W·(m·K)-1,包壳导热系数kc=17 W·(m·K)-1,冷却剂定压比热容cp=5 800 J·(kg·K)-1,平均线功率密度ql=16.1 kW·m-1,对流换热系数h=40 kJ·(m2·K)-1,热管因子F=2.35,冷却剂入口温度Tin=565 K,冷却剂出口温度Tout=601 K[12].考虑到燃料棒的周向对称性和轴向延续性,计算时取1/2燃料棒为计算模型,令其上下壁面为定温边界条件,轴向截面为对称边界,包壳壁面为对流换热,数学表达式为(12)式中:T1(z)为热通道冷却剂的温度;Tcs为包壳外壁面的温度.1.3 温度场传热计算在求解压水堆燃料棒温度场解析解时,做如下假设: ① 轴向释热率呈余弦分布,径向通量展平,即内热源只沿轴向变化; ② 忽略在轴线方向的导热,认为只沿半径方向导热; ③忽略冷却剂、燃料或包壳的所有物理变化,即其各物性参数为常数; ④ 冷却剂始终保持为液相,没有相变换热; ⑤ 忽略外推高度的影响[13].根据上述假设和基本导热微分方程,可求得热通道冷却剂的温度为(13)式中: T1为初始温度为该热通道内冷却剂的质量流量;cp为冷却剂定压比热容;ql(0)为最大线功率密度.包壳外壁面的温度为(14)由于包壳很薄,可以看成无内热源的圆筒壁,则包壳内壁面的温度为(15)在包壳与燃料芯块之间有充满氦气的间隙,尽管气隙厚度很小,但由于其导热率很低,会产生相当大的温降,所以必须考虑气隙导热问题.与包壳类似,把气隙看成均匀的圆筒,则芯块表面的温度为(16)根据有内热源圆柱体导热问题的求解,芯块中心温度为(17)通过式(14)-(17),可以求得燃料棒各点的温度为Rci<r≤Rcs,(18)Ru<r≤Rci,(19)0≤r≤Ru.(20)图2为燃料棒温度分布图,其中实线表示解析解,云图表示数值解,可以看出解析解与数值解得到的温度场吻合良好.图2 燃料棒温度分布图图3为不同半径处沿轴向的温度曲线图,从图3可以更清晰看出:在燃料棒包壳区域解析解与数值解基本吻合,越靠近中心误差越大.这是因为解析计算时由外向内,误差逐步叠加,最大达到4.62%,但仍在合理范围内.同时发现,数值模拟时燃料棒是存在轴向传热的,即很小部分热量会向两端传递,也符合实际情况,因此大多数情况下数值解略小于解析解.图3 不同半径处沿轴向温度曲线图2 燃料棒的(火用)计算与分析前面通过求解数值解和解析解得到了燃料棒的温度场分布,并进行对比验证模型的准确性.在此基础上,从能量与质量相结合的角度,通过(火用)分析方法进一步分析燃料棒传热规律以及能量利用率[14].2.1 核能转化为热能过程从热力学观点来看,核能都是(火用),若忽略裂变过程中能量的损失,核能(火用)从数值上应等于反应堆热功率Q.对于燃料棒上任一微元体积Vu,其平均温度为Tm,释热量为dqv,假设其处于温度为T0=298.15 K的环境中,理论上其最大热量(火用)为(21)根据式(20),燃料芯块任一横截面上0～r范围内平均温度为(22)对于整根燃料棒,核能转化为热能过程中(火用)损为(23)将式(22)代入式(23),得到燃料棒内核能转化为热能过程中(火用)损为(24)2.2 对流换热过程冷却剂流经燃料棒吸热所得(火用)值为(25)式中线热流密度对流换热过程的(火用)损为Exl,c(z)=Ex,u-Ex,c=(26)将式(13)和式(23)代入式(26),即可得冷却剂沿热通道方向的(火用)损分布.2.3 结果分析根据式(23),数值求解得到如图4所示燃料棒(火用)损分布图,燃料棒沿轴向两端(火用)损最小,中心处达到最大,整体分布趋势与功率大小相对应.在中心一定区域内,(火用)损增长速率最小,说明此时释热量和温度变化速率基本相等,但随后随着半径增大迅速增加,最大值出现在芯块边缘附近.图4 燃料棒(火用)损分布图不同半径和不同横截面处的(火用)损和温度曲线分别如图5，6所示，,核能转换过程的(火用)损主要取决于燃料芯块内温度分布,温度越高,能量形式转换所造成的(火用)损越小.同时可以发现:随着半径的增大,沿轴向(火用)损变化速率随着半径的增大而逐渐增大,在z=0的横截面附近达到最大,而越靠近燃料棒两端,(火用)损变化速率越小.这是由于功率越高,温度波动越剧烈,另一方面,燃料棒由内而外传热热阻不断增大,也将导致系统能量品质下降,做功能力降低,(火用)损变大.根据式(24),可以得到核能转换为热能过程中总(火用)损分布情况,如图7所示.不同半径处对应的总(火用)损分布曲线如图8所示,总(火用)损从燃料棒底端向上平稳增加,近似呈线性变化,当燃料芯块r=4.10 mm,z=L/2时,该过程总(火用)损约为150 W,(火用)损系数((火用)损与燃料棒总释热量之比)为0.207,而工程实际中由于各种偏差,该系数必然会有所偏大,因此在热工设计时针对性减小(火用)损系数有着重要意义.图5 沿轴向的(火用)损和温度变化曲线图6 沿径向的(火用)损和温度变化曲线图7 燃料棒总(火用)损分布图图8 不同半径处总(火用)损变化曲线根据式(26),可得冷却剂沿热通道方向(火用)损分布,冷却剂沿热通道的(火用)损分布和温度变化曲线如图9所示,(火用)损先增大后减小,而不是与温度一样逐渐增大,这是因为对流换热过程中(火用)损主要取决于燃料芯块与冷却剂之间的传热温差,传热温差越大,(火用)损越大.冷却剂沿热通道的累积(火用)损变化曲线如图10所示,累积(火用)损的变化趋势与温度相似,在热通道中部增长速率较快,在热通道两端增长较慢,该过程累积(火用)损为219 W,相应的(火用)损系数为0.304,两图可相互印证. 图9 冷却剂沿热通道的(火用)损分布和温度变化曲线图10 冷却剂沿热通道的累积(火用)损变化曲线3 结论1) 提高能量利用率的本质就是减小(火用)损,燃料棒核能转换为热能过程的(火用)损主要取决于燃料芯块的温度,沿轴向先增大后减小,沿径向不断变大;在燃料芯块边缘处达到最大值,该过程(火用)损系数为0.207.2) 影响燃料棒与冷却剂对流换热过程(火用)损的主要因素是燃料芯块与冷却剂之间的传热温差,温差越大,(火用)损越大,该过程总(火用)损系数为0.304.3) 通过温度场和(火用)损分析方法的结合,可以对压水堆堆芯传热过程的优劣程度进行可靠性评估,也能够为优化堆芯稳态热工设计、核燃料装载和冷却剂流量分配方面提供有益参考.参考文献(References)[ 1 ] 张蕊,干富军,左巧林,等.压水堆燃料棒束通道内过冷沸腾分析[J].原子能科学技术,2015,49(9):1579-1585.ZHANG R, GAN F J, ZUO Q L, et al. Analysis of subcooled boiling in PWR rod bundle channel[J].Atomic Energy Science andTechnology,2015,49(9):1579-1585.(in Chinese)[ 2 ] 宋磊,郭赟,曾和义.板状燃料组件入口堵流事故下流场和温度场的瞬态数值计算[J].核动力工程,2014,35(3):6-10.SONG L, GUO Y, ZENG H Y. Numerical analysis on transient flow and temperature field during inlet flow blockage accidents of plate-type fuel assembly[J]. Nuclear Power Engineering,2014, 35(3):6-10. (in Chinese) [ 3 ] 卢川,严明宇,毕树茂,等. 基于CFD方法的行波堆19燃料棒束流固耦合传热特性研究[J].原子能科学技术,2015,49(12):2170-2175.LU C, YAN M Y, BI S M, et al. Study on fluid-solid coupling heat transfer characteristics of TWR assembly with 19 fuel pins based on CFD method[J]. Atomic Energy Science and Technology, 2015, 49(12):2170-2175. (in Chinese)[ 4 ] 罗磊,陈文振,陈志云,等.单个燃料元件热工水力三维数值模拟[J].海军工程大学学报,2011,23(1):63-66.LUO L, CHEN W Z, CHEN Z Y, et al. Numerical simulation of thermal hydrodynamic of single reactor fuel rod[J].Journal of Naval University of Engineering,2011,23(1):63-66. (in Chinese)[ 5 ] SALAMA A, EL-DIN EL-MORSHEDY S. CFD simulation of flow blockage through a coolant channel of atypical material testing reactor core[J]. Annals of Nuclear Energy, 2012, 41: 26-39.[ 6 ] LI X C, GAO Y. Methods of simulating large scale rod bundle and application to a 17×17 fuel assembly with mixing vane spacer grid[J]. Nuclear Engineering and Design, 2014, 267: 10-22.[ 7 ] FRICANO J W, BAGLIETTO E. A quantitative CFD benchmark for solidium fast reactor fuel assembly mode-ling[J]. Annals of Nuclear Energy, 2014, 64: 32-42.[ 8 ] PIRO M H A, LEITCH B W. Conjugate heat transfer simulations of advanced research reactor fuel[J]. Nuclear Engineering and Design, 2014, 274: 30-43.[ 9 ] RASU N G, VELUSAMY K, SUNDARARAJAN T, et al. Simultaneous development of flow and temperature fields in wire-wrapped fuel pin bundles of sodium cooled fast reactor[J]. Nuclear Engineering and Design, 2014, 267: 44-60.[10] LIU C C, FERNG Y M, SHIH C K. CFD evaluation of turbulence models for flow simulation of the fuel rod bundle with a spacer assembly[J]. Applied Thermal Engineering, 2012, 40: 389-396.[11] ZHANG M. Modeling of radiative heat transfer and diffusion processes using unstructured grid[D]. Cookeville: Tennessee Technological University, 2000.[12] 闵元佑,黄云.秦山核电二期工程反应堆及反应堆冷却剂系统设计[J].核动力工程, 2003,24(2):1-7.MIN Y Y, HUANG Y. Design of the reactor and reactor coolant system for qingshan phase II NPP project[J]. Nuclear Power Engineering, 2003,24(2):1-7. (in Chinese)[13] 陈文振,于雷,郝建立.核动力装置热工水力[M].北京:中国原子能出版社,2013.[14] 彭敏俊,田兆斐.核动力装置热力分析[M]. 哈尔滨:哈尔滨工程大学出版社,2012.。