生物力学物质的粘弹性全解
- 格式:ppt
- 大小:1.21 MB
- 文档页数:64




第七章、粘弹性7.1 基本概念弹性:外力 外力撤除 粘弹性 弹性+粘性 →形变 →应力 →储存能量→能量释放 →形变恢复 粘性:外力 外力撤除 →形变 →应力 →应力松弛 →永久形变→能量耗散理想弹性:服从虎克定律σ=E·ε应力与应变成正比,即应力只取决于应变。
εtσ/Et t 0dt d εησ⋅=εtσ/ηt 0 理想粘性:服从牛顿流体定律 应力与应变速率成正比,即应力只取决于应变速率 dt d εησ⋅=牛顿流体定律的比例常数为粘度ηdtd εησ⋅=dtdx y y x dt d dt d ⋅==1)(εyx应变速率为速度梯度∴粘度η等于单位速度梯度时的剪切应力,反映了分子间由于相互作用而产生的流动阻力,即内摩擦力的大小,单位为Pa·S弹性(1)储能:能量储为应变能(2)可逆:记忆形状,(3)瞬时:不依赖时间E=E(σ, ε, T)虎克固体(1)耗能:能量耗为热能(2)不可逆:无形状记忆(3)依时:应变随时间发展E=E(σ, ε ,T, t)牛顿流体粘性熵弹性聚合物是典型的粘弹体聚合物是典型的粘弹体粘性:分子链滑移,应力松弛拉伸应力松弛聚合物的应力松弛:t7.2 静态粘弹性受恒定应力或应变的作用E=E(σ, ε ,T, t)7.2.1 静态粘弹性现象(1)蠕变:在一定的温度和恒定应力的作用下,观察试样的应变随时间增加而增大的现象。
理想弹性体:σ=E·εεtσ/E应力恒定,故应变恒定εtσ/η理想粘性体 dtd εησ⋅=应力恒定,故应变速率为常数,应变以恒定速率增加聚合物:粘弹体①理想弹性,即瞬时响应: 由键长、键角提供②推迟弹性形变,即滞弹部分:③粘性流动:链段运动整链滑移 εt①③ ②εt εt线形聚合物 交联聚合物(2)应力松弛:在一定的温度和恒定应变的作用下,观察试样的应力随时间增加而衰减的现象。
σtE·ε理想弹性体:σ=E·ε 应变恒定,故应力恒定σt理想粘性体 dtd εησ⋅=应变恒定,应变速率为0,故应力为0聚合物:粘弹体σ tσ0交联聚合物线形聚合物由于交联聚合物分子链的质心不能位移,应力只能松驰到平衡值7.2.2. 线性粘弹性模型线性粘弹性:可由服从虎克定律的线性弹性行为和服从牛顿定律的线性粘性行为的组合来描述的粘弹性。





生物粘弹性力学研究及其应用生物是自然界中最为神奇的存在之一。
生物体内的分子、细胞、组织和器官之间存在着复杂的物理和化学相互作用,并且这些相互作用是在生物材料的粘弹性力学特性的基础上发生的。
近年来,生物粘弹性力学研究成为了研究生物组织结构、机能和疾病发展机制的重要手段,具有广泛的应用前景。
一、什么是生物粘弹性力学?生物粘弹性力学是研究生物材料的粘性和弹性力学特性的一种学科,它关注材料应变随时间变化的行为和其形状变化的响应。
生物材料不同于普通材料,其会在应变阈值之后表现出所谓的“粘液”特性,在剪切应力加载之后会表现出流变作用。
生物材料中的许多功能基于这种特性,包括细胞的运动和伸展、组织的生长和自愈性等。
粘弹性力学相关的测量技术可以准确地测量生物材料的粘性和弹性特性,并进一步用于诊断和治疗。
二、生物粘弹性力学的应用领域1. 细胞生物力学研究生物粘弹性力学研究可以帮助人们更好地了解细胞中组成分子之间的相互作用,有助于发现疾病早期变化的迹象。
因为不同类型和不同健康状态的细胞具有不同的弹性和粘性特性,因此研究生物材料的粘弹性力学特性可以帮助人们更好地理解健康和疾病之间的关系。
2. 生物材料的医学应用生物材料在医学领域中得到了广泛的应用,如人工骨、假肢、软组织治疗和组织再生等。
研究生物材料的粘弹性力学特性可以帮助人们更好地设计和制造这些器械,以更好地适应人体的需要。
3. 疾病早期诊断在不同疾病的发病过程中,细胞和组织的粘弹性力学特性会发生变化。
比如,在某些情况下,肿瘤细胞比正常细胞更加柔软。
测量这种变化可以帮助人们发现疾病的早期变化,以便及早采取治疗。
三、生物粘弹性力学测量技术1. 微管道微管道是一种功能强大的工具,它可以用于精确测量生物材料的粘弹性力学特性。
不仅可以测量细胞和组织的流变学行为,还可以测量单个生物分子的弹性和粘性特性。
2. 原子力显微镜原子力显微镜可以用于测量材料的微米和纳米尺度的形变,可以在原子尺度下研究材料的弹性和粘性特性。

第七章 聚合物的粘弹性viscoelasticity§7-1概述7.1.1 对粘性和弹性的认识过程1 起初的认识16世纪左右,在欧洲,自然科学开始萌芽。
那时候,人们对物质形态有了初步认识,但还是比较初级的认识。
那时候科学家认为,要么是纯粘性液体,要么是纯弹性固体。
(1) 理想粘性液体理想粘性液体(牛顿流体),其应力-应变行为服从牛顿流动定律d dt εση= 式中:σ——应力;d dt ε——应变速度;η——本体粘度。
积分上式并令:t =0,ε=0,得 t σεη= 例如大多数小分子液体可近似地看作理想粘性液体。
理想粘性液体的特点是:应变速率与应力成正比;形变随时间的延长而发展;当除去外力之后形变不可回复。
(2) 理想弹性固体对于理想弹性体,其应力-应变关系服从胡克定律,即E σε=式中:σ——应力;E ——弹性模量;ε——应变。
例如金属、玻璃、玻璃态的高聚物都可近似看作理想弹性固体。
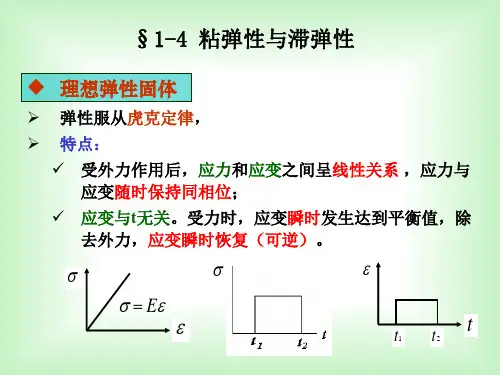
理想弹性固体的特点是:应变与应力成正比,应变在加力的瞬时达到平衡值;除去应力时,应变瞬时回复。
2 认识的发展后来,人们逐渐认识到,粘性和弹性都不是绝对的,而是相对性的。
在某些条件下主要表现弹性;而在另一些条件下主要表现粘性。
比如硬物快速地撞击水面,会被弹起来。
这就是说,即使所谓的纯粘性液体在某些条件下也会表现固体的弹性。
再譬如,古老的教堂里的窗玻璃,现在发现上面变薄了,下面变厚了。
这就是说,即使像玻璃这样“非常固体”的固体,经过很长时间之后也表现出液体的流动。
为了定量地说明弹性和粘性的相对性,可用下面的公式:材料内部分子运动的松弛时间………(物质的本性)———————————————实验观察时间(或外力作用速度)……(外部条件)如果<<1,则表现出液体粘性;如果>>1,则表现固体的弹性。
如果≈1,既表现固体的弹性也表现液体的粘性,即粘弹性。
比如,液体水分子的松弛时间大约是10-12秒;而玻璃态高聚物的链段运动的松弛时间达到小时、天、月的数量级。