上海交通大学自控考研试卷

同学，你好！如果你打算考上海交大，那么请你花几分钟看下这份文档，这将改变你的一生！本人为交大在校学生，以下资料都是自己历年来在交大收集的第一手资料，全都出自于历届学长学姐，本人花高价收购而来！虽然市面上还有很多人可提供这些科目资料，但他们很多人本身就不是来自交大，对交考研根本不了解。

当然其中也有一些来自交大，但他们大都离开交大好几年了，交大自07年开始考研就已经改革，而他们提供的一些资料早已不适合现今交大的考研。

考研不同于高考，高考科目全部都是统编，但考研专业课的考试确实一门很大的学问，我这的资料很多都来自官方版权威的资料（网上很多电子其实都是照片，而且真题答案都是请人做的，不少答案都是错的，而我这边的材料都来自往年交大自己办考研班的时候发的资料，绝对权威），还有一部分是从历届学长学姐那收购而来，如果有必要我可以帮你找学长和你交流，最主要的是可以为你提供交大考研专业课的信息，这样就可以使你和交大的学生站在同一起跑线上，不会输在专业课的起跑线上，相对于别的同学外校考研，那你就更有优势了！考研也是一种投资，投资好了，你就会得到相当大的回报，可能你会觉花钱就会觉得不值，但当你以一两分的优势就力压群雄的话，那时你就会发现发这份钱很值了，考研每一分都对你很重要，而我所希望做的就是让你专业课的起点至少和交大本部学生一样高，绝不让考研输在专业课上！现在我已经可以提供以下科目资料，如果这下面有你要报考的专业的话，无疑这对你来说是一个最大的喜讯！如果你需要这些资料，请联系yangweitu@或QQ1449791880或上海交大考研淘宝店/!资料还是实时更新中，如果这里没有你想要的资料，也可来邮询问是否已经收集到你想要的资料！●上海交通大学<经济学>考研专业课资料（代码841）●上海交通大学/上海交大<金融学844>历年考研真题和辅导资料最近和一些同学接触后，让我感觉我很有必要写出如下这段话，如果大家有时间的话，就看看吧！大家都是怀揣梦想的有志者，都希望都过各种渠道获得最多最好的专业课资料，但这个市场鱼龙混杂，资料质量参差不齐，一份好的资料可以助你一臂之力，但一份差的资料也有可能影响你的一生。

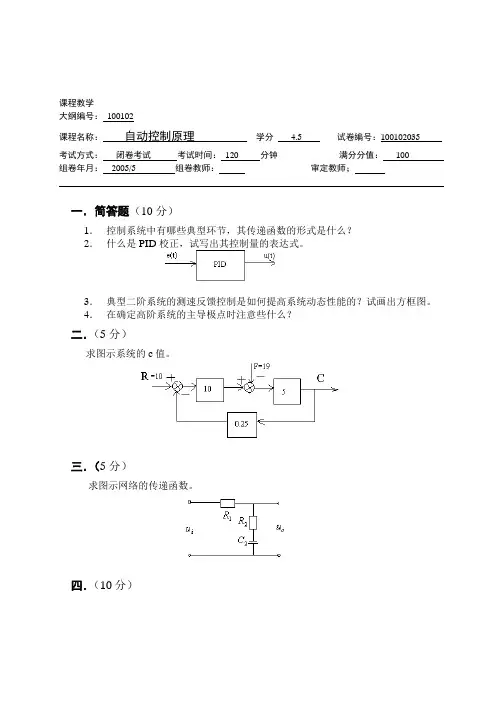
课程教学大纲编号：100102课程名称：自动控制原理学分 4.5 试卷编号：100102035考试方式：闭卷考试考试时间：120 分钟满分分值：100组卷年月：2005/5 组卷教师：审定教师；一．简答题（10分）1．控制系统中有哪些典型环节，其传递函数的形式是什么？2．什么是PID校正，试写出其控制量的表达式。

3．典型二阶系统的测速反馈控制是如何提高系统动态性能的？试画出方框图。

4．在确定高阶系统的主导极点时注意些什么？二．（5分）求图示系统的c值。

三．（5分）求图示网络的传递函数。

四．（10分）有一位置随动系统，其结构如图所示，其中1040.,k ==τ，当输入量)t (r 为单位阶跃函数时，求系统的自然振荡角频率n ω，阻尼比ξ和系统的暂态指标)05.0?(%,=∆σs t 。

五．（12分）设某系统的方框图如图示，若系统以2=ω弧度/秒的频率作等幅振荡，试确定振荡时参数k 与a 之值。

六．（13分）设系统结构如图所示，试确定闭环系统的稳定性。

七．（15分）系统的特征方程为04423=+++a s s s ，求以a 为参数的根轨迹，并求使系统阻尼比为0.5的a 的值。

八.(5分)根据图示最小相位系统的对数幅频特性,写出该系统的开环传递函数,并画出相频特性大致图形。

九.(10分)试分析图示系统在正弦控制信号t sin A )t (r ω=作用下的稳态误差，图中时间常数T 及开环增益k 均为常数。

十.(15分)设控制系统的开环传递函数为)2.01)(4.01(20)()(s s s s H s G ++=, 1. 分析系统的稳定性及稳定裕度；2. 采用传递函数s .s .)s (G c 0201201++=的校正装置，问该校正是何种校正,分析校正后系统的稳定性及稳定预备.3. 绘制校正前后系统的伯德图。

目　录2014年上海交通大学816自动控制理论考研真题（回忆版）2013年上海交通大学自动控制理论考研真题（回忆版）2012年上海交通大学自动控制理论考研真题（回忆版）2011年上海交通大学自动控制理论考研真题（回忆版）2007年上海交通大学405自动控制理论考研真题
2003年上海交通大学405自动控制理论考研真题
2002年上海交通大学460自动控制理论考研真题
2001年上海交通大学460自动控制理论考研真题
2014年上海交通大学816自动控制理论考研真题（回忆版）
2013年上海交通大学自动控制理论考研真题（回忆版）
2012年上海交通大学自动控制理论考研真题（回忆版）
2011年上海交通大学自动控制理论考研真题（回忆版）
2007年上海交通大学405自动控制理论考研真题
2003年上海交通大学405自动控制理论考研真题
2002年上海交通大学460自动控制理论考研真题
2001年上海交通大学460自动控制理论考研真题。

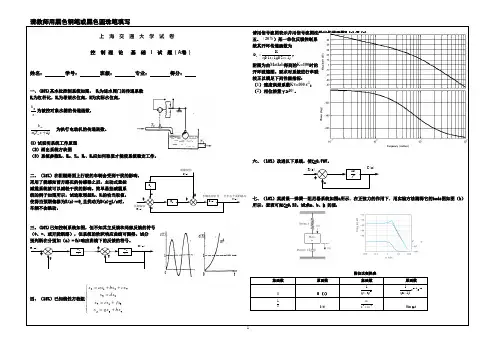
2018年上海交通大学 816自动控制理论真题回忆版 回忆人：Joshua Lee （2018年研究生入学考试考生）试题总分150分，共8个大题.第一题（15分）：图1-24为水温控制系统原理示意图。

冷水在热交换器中由通入的蒸汽加热，从而得到一定温度的热水。

冷水流量变化用流量计测量。

1. 为保持水温为给定值，请解释系统是如何工作的.2. 指出系统的被控对象和控制器。

3. 画出系统的方框图。

（本题是胡寿松主编的《自动控制原理》（第六版）第一章课后习题1-4，属于热身题，基础题，送分题！）第二题（20分）：给了你两个系统方框图，二者很类似，仅有细微差别。

每一个系统方框图都有输入()R s 和扰动()N s ，输出为()Y s ,让你求()()Y s R s 和()().Y s N s（实质为考查方框图的化简和叠加原理，基础题，送分题）第三题（15分）：一系统如图所示，里面含有一个参数K ，让你求系统在超调量0.2p M =和峰值时间为0.8秒时参数K 的值，并求此时系统的上升时间和调整时间。

允许误差为2%∆=（实质为考查二阶系统的性能指标，简单题，直接套公式，送分）第四题（15分）：考查根轨迹法。

第五题（20分）：给你一个系统的对数幅相曲线，让你确定参数的值使得系统稳定。

第六题（25分）：告诉你一个单位反馈系统的开环传递函数()K G s ，让你设计串联超前校正装置使系统的相角裕度o 50γ≥，截止频率大于5/.rad s第七题（20分）：一个非线性系统由线性部分和非线性部分组成，其中非线性环节的描述函数为()4,N N πω=。

让你绘制线性部分的奈奎斯特曲线和非线性部分的1N -曲线，并说明系统必存在稳定的自振荡点.第八题（20分）：给你一个系统结构图，试用状态反馈方法，将系统闭环极点配置在－3，-1，4处，并求解系统的状态空间模型和传递函数。

评价：总体而言，今年专业课816考题中规中矩，没有偏题、怪题，好好复习应该可以取得一个不错的分数。

2017上海交通大学考研816自动控制原理考研真题
一、用冷却水在热交换器中冷却热物料到要求的温度，要求画出满足要求的闭环系统框图，并指出控制对象，控制变量，操纵变量
二、根据信号流图求传递函数。

三、根轨迹。

不难，不过需要先求出等效开环传递函数。

四、超前矫正，给出了矫正后的Kv和相角裕度
五、二阶动态性能指标。

告知超调量和峰值时间，求传递函数，上升时间，调节时间
六、奈奎斯特稳定判据。

四个小题。

由图像特点，开环极点数，系统类型，判稳定。

七、非线性，给出了-1/N和G(jw)图像，分析两曲线交点处的系统稳定性。

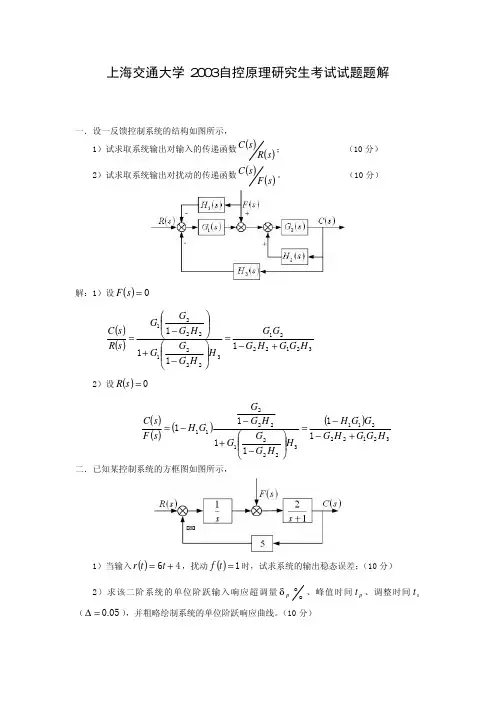
上海交通大学2007年硕士研究生入学考试试题试题序号：805试题名称： 控制理论基础（答案必须写在答题纸上，写在试题纸上的一律不给分）一、（10分）什么事非线性系统的极限环振荡它与临界稳定的线性系统的等幅振荡主要有哪些区别二、（15分）一个简单的水位调节系统有水箱、浮球、杠杆机构、及进出水阀门等组成，如图（a ）所示。

显然，如果阀门2的开度不断地发生变化，改变出水流量，会引起水箱水位发生波动；而水箱水位的变化会通过浮球和杠杆带动阀门1，从而使进水流量发生变化，假定进水流量与液位（分别设为1Q 和h ）的关系如图（b ）所示。

试问：当阀门2的开度保持不变时，系统是否可能有平衡状态如有的话，请说明1） 应该如何确定平衡状态下的水位和流量2） 实际水位偏离平衡水位时，系统如何工作，最后实际水位是否能回到平衡水位三、（20分）已知电路如图，设1R =9k Ω，2R =1k Ω，2C =10μF 。

试求出其传递函数，并通过其波德图说明该电路有何种相应调节作用，最大相位调节量是多大更多资源：四、（20分）以下两个系统方块图中，大写字母均表示传递函数，小写字母均表示输入或输出信号。

试将图（a ）所示的系统等价变换为图（b ）所示的系统，求出相应的传递函数)(s P 、)(s Q ；另外，请以d 为输入e 为输出，求系统的传递函数)(/)(s D s E 。

五、（30分）设单位反馈系统开环波德图的渐进折线如下，已知这是一个最小相位系统，其闭环增益稳定裕量为20dB ，其他条件如图所示1） 试求系统开环传递函数，并请计算（或估算）其相应的相位稳定裕量 2） 若要求系统的相位稳定裕量为45，应如何调整开环增益（用符号K 表示）3） 为保持系统闭环稳定，K 应在什么范围内取值六、（20分）假定有一复合控制系统如图所示，其输入信号为t t r )(，且被控制对象的参数0K 和0T 为已知。

1） 为使系统的稳态误差严格为零，前馈控制环节的参数f K 应如何设定2） 这个方法在实际实现时可能会有什么问题吗如有的话，还应该怎么办七、（20分）一阶单位反馈系统如图（a ）所示，现欲通过实验确定参数T 。

上 海 交 通 大 学二〇一三年攻读硕士学位研究生入学考试试题考试科目: 自动控制原理注意:答案必须写在答题纸上,写在试卷或草稿纸上均无效。

1.（10分）系统结构如下图所示，求系统的超调量%σ和调节时间s t 。

2.（10分）求图1所示无源网络的运动方程和传递函数，图中电压1()u t 和2()u t 分别为输入量和输出量。

2()t 3.（15分）已知系统的结构如图所示，其中(0.51)()(1)(21)k s G s s s s+=++，输入信号为单位斜坡函数，求系统的稳态误差。

分析能否通过调节增益 k4.(15分)设负反馈系统如图2 ，前向通道传递函数为10()(2)G s s s =+，若采用测速负反馈()1s H s k s =+，试画出以s k 为参变量的根轨迹(10分)，并讨论s k 大小对系统性能的影响(6分)。

5.（20分）已知一控制系统的结构图如下，1）确定该系统在输入信号()1()r t t =下的时域性能指标：超调量%σ，调节时间s t 和峰值时间p t ；2）当()21(),()4sin 3r t t n t t =⋅=时，求系统的稳态误差。

6.(20分)某火炮指挥系统结构如下图所示，()(0.21)(0.51)K G s s s s =++系统最大输出速度为2 r/min，输出位置的容许误差小于2o ，求：1）确定满足上述指标的最小K 值，计算该K 值下的相位裕量和幅值裕量；2）前向通路中串联超前校正网络0.41()0.081c s G s s +=+，试计算相位裕量。

7.(20分)设单位负反馈控制系统的开环传递函数为2()(2)(1)o K G s s s s s =+++，试确定使系统稳定的K 的取值范围。

如果想让闭环极点位于1s =-之左，K 应取何值。

8. (20分) 设单位负反馈系统开环传递函数如下，试概略绘出相应的闭环根轨迹图，并确定分离点坐标d 和临界增益K c 。