运筹学 第11章-决策分析
- 格式:ppt
- 大小:403.00 KB
- 文档页数:26

运筹学知识点运筹学是一门综合运用数学、逻辑、计算机科学等方法与技巧来解决现实世界中最优化问题的学科。
它涉及决策分析、优化模型、算法设计等多个方面的知识点。
在本文中,我将介绍一些运筹学的重要知识点,并探讨其在实际生活和工作中的应用。
首先,决策分析是运筹学的核心方向之一。
决策分析旨在帮助决策者做出理性和最佳的决策。
它涉及问题定义、信息收集、模型构建、方案评估等多个步骤。
决策分析的一个重要工具是决策树,它通过图形化地表示决策的各个阶段和可能的结果,帮助决策者清晰地分析决策过程中的风险和潜在回报。
举个例子,假设我们要决定是乘坐公共交通还是开车去上班。
我们可以构建一个决策树,考虑到可能的交通状况、费用、时间等因素,帮助我们做出最佳的选择。
其次,优化模型是运筹学的另一个重要知识点。
优化模型通过数学公式和约束条件来描述一个问题,并寻找满足目标的最优解。
常见的优化模型包括线性规划、整数规划、非线性规划等。
线性规划是一种最常用的优化模型,它适用于一些具有线性关系的问题。
整数规划则适用于需要整数解的问题。
非线性规划则考虑了更为复杂的问题情况,可以通过各种算法进行求解。
优化模型在很多领域有着广泛的应用,如生产调度、物流运输、资源分配等。
举个例子,假设我们是一家制造商,我们希望通过优化生产调度来最大化利润。
我们可以使用线性规划模型来考虑各个产品的生产时间、产能、销售量、成本等因素,并寻找到一个最优的生产计划。
此外,算法设计也是运筹学的重要内容之一。
算法是为解决特定问题而设计的一系列步骤和操作。
在运筹学中,算法设计通常与优化模型紧密相关。
例如,针对某个优化模型,我们可以设计一种有效的求解算法,以找到最优解。
常见的算法包括贪心算法、动态规划、启发式算法等。
这些算法都有各自的特点和适用范围。
举个例子,假设我们需要在一个迷宫中找到一条最短的路径。
我们可以使用动态规划算法来计算每个位置到终点的最短距离,并依次进行路径选择,直到找到一条最短路径。

运筹学中的决策分析与风险管理运筹学是一门综合应用数学的学科,通过运用数学模型和方法来解决实际问题。
在这个领域中,决策分析和风险管理是非常重要的内容。
本文将介绍运筹学中的决策分析和风险管理,并探讨它们在实际中的应用和重要性。
一、决策分析决策分析是一种科学的方法,旨在帮助决策者在面对复杂问题时做出最佳决策。
在决策分析中,决策者需要收集和分析相关数据,应用数学模型和技术来评估各种不同决策方案的风险和回报。
通过这种方法,决策者可以更好地理解决策问题的各种潜在结果,并选择最优的决策方案。
决策分析通常包括以下几个步骤:1. 问题定义:明确问题的目标和约束条件,并确定决策的范围。
2. 数据收集与分析:收集相关数据,并利用数学模型和统计方法对数据进行分析。
3. 模型建立:根据问题的特点和决策者的需求,选择合适的数学模型,并将问题转化为数学模型。
4. 解决方案评估:评估各种决策方案的风险和回报,并对它们进行比较和优化。
5. 决策实施:根据评估结果选择最佳决策方案,并付诸实施。
在实际应用中,决策分析可以帮助企业管理者制定营销策略、生产计划和供应链管理方案等,从而提高业绩和效益。
二、风险管理风险管理是指通过识别、分析和评估风险,并采取相应的措施来降低和控制风险,并在必要时应对可能出现的风险事件。
在运筹学中,风险管理可以帮助决策者更好地处理不确定性,并最大程度地保护企业的利益。
风险管理通常包括以下几个方面:1. 风险识别:根据问题的特点和环境的变化,识别可能出现的各种风险。
2. 风险分析和评估:对已识别的风险进行定量或定性的分析和评估,确定其发生的概率和影响程度。
3. 风险应对:根据分析和评估的结果,制定相应的风险应对策略,并制定相应的预案和措施。
4. 风险监控与控制:建立有效的监控和控制体系,及时发现和处理风险,并防止风险事件的扩散和蔓延。
通过风险管理,企业可以更好地预测和应对不确定性,减少潜在的损失,并提高业务的可持续发展能力。

运筹学优化问题和决策分析的方法运筹学是一门应用数学学科,旨在通过建立数学模型来解决决策问题,并运用优化算法寻找最优解。
在现代社会中,运筹学的应用已经渗透到各个领域,包括供应链管理、物流规划、生产调度等。
本文将介绍运筹学中的优化问题和决策分析的方法。
一、优化问题的基本概念在运筹学中,优化问题是指在一定的约束条件下,寻找某个指标的最优解。
优化问题可以分为线性优化问题和非线性优化问题。
线性优化问题的目标函数和约束条件都是线性的,而非线性优化问题的目标函数和约束条件涉及非线性关系。
在解决优化问题时,通常会使用数学建模的方法。
首先,将实际问题抽象为数学模型,然后建立数学模型的目标函数和约束条件。
接下来,运用优化算法求解模型,得到最优解。
二、常用的优化算法1. 线性规划线性规划是指优化问题的目标函数和约束条件都是线性的情况。
线性规划常常可以用单纯形法来求解,该方法通过迭代计算,逐步逼近最优解。
2. 非线性规划非线性规划是指优化问题的目标函数和约束条件涉及非线性关系的情况。
在求解非线性规划问题时,可以使用梯度下降法、牛顿法等方法。
3. 整数规划整数规划是指优化问题的变量需要取整数值的情况。
整数规划问题通常更加复杂,可以使用分支定界法、割平面法等算法求解。
三、决策分析的方法决策分析是指运用数学建模和分析方法来帮助决策者做出最佳决策。
决策分析的方法包括多属性决策分析、决策树分析、动态规划等。
1. 多属性决策分析多属性决策分析是指在考虑多个决策指标的情况下,综合分析各个指标的权重和价值,从而做出最佳决策。
常用的多属性决策分析方法包括层次分析法、模糊综合评判法等。
2. 决策树分析决策树分析是一种通过构建决策树来辅助决策的方法。
决策树是一种具有树状结构的决策模型,通过分析各个决策路径上的概率和收益来进行决策。
3. 动态规划动态规划是一种递推和状态转移的方法,常用于求解多阶段决策问题。
动态规划将决策问题分解为一系列子问题,并通过逐步求解子问题来求解原问题的最优解。


运筹学教程胡运权第5版1. 简介《运筹学教程》是一本经典的运筹学教材,由胡运权教授编写,已经出版了第5版。
本教程旨在介绍运筹学的基本概念、方法和应用,帮助读者掌握运筹学的基本原理和技巧。
2. 内容概述本教程分为十个章节,涵盖了运筹学的主要内容。
第一章:运筹学概述本章介绍了运筹学的基本概念和发展历程,阐述了运筹学在现代管理决策中的重要作用。
第二章:线性规划本章介绍线性规划的基本概念、模型和求解方法,包括单纯形法和对偶理论等内容。
第三章:整数规划本章介绍整数规划的基本概念和求解方法,包括分枝定界法和割平面法等内容。
第四章:非线性规划本章介绍非线性规划的基本概念和求解方法,包括梯度法和牛顿法等内容。
第五章:动态规划本章介绍动态规划的基本概念和求解方法,包括最优子结构和状态转移方程等内容。
第六章:网络优化本章介绍网络优化的基本概念和求解方法,包括最小生成树和最短路问题等内容。
第七章:多目标规划本章介绍多目标规划的基本概念和求解方法,包括帕累托最优解和权衡法等内容。
第八章:排队论本章介绍排队论的基本概念和模型,包括利用泊松分布和指数分布建模等内容。
第九章:库存管理本章介绍库存管理的基本概念和模型,包括经济订货量和安全库存等内容。
第十章:决策分析本章介绍决策分析的基本概念和方法,包括决策树和期望值法等内容。
3. 学习目标通过学习本教程,读者可以掌握以下技能:•理解运筹学的基本概念和方法;•掌握线性规划、整数规划、非线性规划等方法的应用;•学会运用动态规划、网络优化、多目标规划等方法解决实际问题;•掌握排队论、库存管理、决策分析等方法的应用。
4. 使用说明读者可以将本教程作为自学资料,按照章节顺序逐步学习。
每个章节都包括基本概念的讲解、求解方法的介绍和案例分析。
在阅读本教程时,读者可以使用Markdown文本格式进行标注和整理笔记。
Markdown具有简单易学、格式清晰的特点,适合用于文档编写和批注。
5. 结语《运筹学教程》是一本经典的运筹学教材,适合作为运筹学的入门教材或者参考资料。


运筹学与决策分析在交通运输中的应用随着交通运输行业的不断发展,越来越多的人们选择了旅行或使用交通工具来进行海陆空物流。
我们所知道的交通运输已经成为了建设现代化社会和促进经济发展的重要因素。
如何优化交通运输的效率和品质已成为各国政府和企业所关注的一个问题。
运筹学与决策分析技术应用于交通运输行业,将会对该行业的管理和发展起到积极的推动作用。
1、运筹学的定义及其应用运筹学是一种研究如何通过制定规定来优化决策的学科。
这个过程通常涉及多种不同类型的变量,如业务参数、资源限制、质量措施和风险因素等。
在交通运输中,运筹学主要解决如何利用数据、建模、预测和优化这一复杂的运输体系,从而使交通运输所需的时间、成本和质量到达最优状态。
例如,优化配送路线、物流规划、仓储场所的分配和估计供应和需求等问题。
2、决策分析的定义及其应用决策分析是一种量化和分析方法,用于评估在通常存在的不确定性和风险下制定决策的潜在影响。
在交通运输中,决策分析通常涉及到经济分析、技术分析、环境分析和政策分析等多方面的影响。
通过分析可能的风险和收益,来制定合理的决策从而减少风险并提高效益。
例如,在交通运输中,决策分析可用于评估不同的运输方案、管理方案和交通运输政策,以支持最终的决策。
3、应用运筹学和决策分析的案例A、运筹学应用案例:中国顺丰速递(SF Express)利用运筹学和人工智能将其物流配送效率提高了40%。
该公司利用自身丰富的数据,通过用途推理和价值自适应的优化算法,实现了产品配送的可预测性,从而提高了配送效率。
B、决策分析应用案例:加拿大航空利用决策分析技术来提高维护效率,从而降低成本。
该公司通过制定决策树,来决定机载设备何时需要进行维修和更换,从而保持正常的航班运行,并且在维修和更换方面减少了 30% 的成本。
4、结论在今天技术不断发展的社会,运筹学和决策分析技术正在逐步引起人们的重视和关注。
在交通运输行业中,利用运筹学和决策分析的技术来优化经营成本和资源分配将成为一个必不可少的选择。


决策分析与运筹学一、引言决策是人们在生活中经常面临的问题,无论是个人还是组织,都要进行决策。
然而,由于信息的不对称、不确定性和复杂性,决策往往会带来巨大的风险。
因此,需要一种科学的方法来辅助我们进行决策,决策分析和运筹学应运而生。
二、决策分析决策分析是以信息、模型和计算为基础的一种决策方法。
它采用定量方法对决策进行分析和评估,从而使决策者获得更清晰的认识和更准确的预测。
常用的决策分析方法包括多属性决策分析、层次分析法和决策树等。
多属性决策分析指的是当决策对象存在多个属性时,通过对多个属性的评估,进行权重的确定,从而综合比较各选项的利弊。
它可以用于复杂的决策问题,如选址、投资决策等。
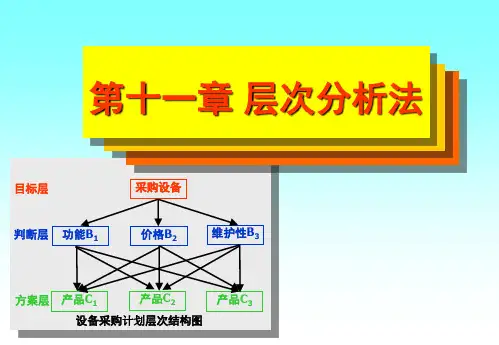
层次分析法是一种基于分级权重的决策分析方法,它通过构建决策层次结构和定量化各因素之间的重要性关系,实现了对决策对象的逐层分析和权重确定。
层次分析法常用于复杂的决策问题,如市场调研、供应链优化等。
决策树是一种决策分析的可视化方法,它通过构建一棵树形结构,使决策问题变得直观而易于理解。
决策树可以应用于分类、预测和优化等问题,如客户流失预测、电商平台推荐算法等。
三、运筹学运筹学是应用数学、统计学和计算机科学等工具和技术解决实际问题的一门学科。
它以最大化或最小化目标函数为目标,通过构建数学模型和优化算法,寻求最优解。
常用的运筹学方法包括线性规划、整数规划和蒙特卡罗模拟等。
线性规划是一种通过线性模型来寻找最优解的方法,在经济、管理和运输等领域得到广泛应用。
例如,用线性规划模型可以实现最小成本配送、最佳产量分配等。
整数规划是线性规划的扩展,它在目标函数、决策变量或限制条件上增加了整数条件。
整数规划可以用于很多特殊问题,如最佳固定资产重复购置决策、生产调度等。
蒙特卡罗模拟是一种通过模拟随机事件来获得概率分布的方法。
它可以应用于很多领域,如金融风险评估、自然灾害预测等。
四、应用案例决策分析和运筹学在实践中得到广泛的应用。
例如,智能制造领域中的生产调度问题,通过运筹学的方法,可以实现对机器和物料的优化排产,从而提高生产效率和减少成本。
运筹学中的优化问题与决策分析优化问题和决策分析是运筹学的核心内容之一。
通过运筹学的方法,可以在复杂的决策情境中找到最优解或最优策略,以达到最大利益或最小成本的目标。
本文将介绍运筹学中的优化问题和决策分析的基本概念、方法和应用。
一、优化问题的基本概念优化问题是指在给定的一组限制条件下,寻找使目标函数取得最大值或最小值的变量取值。
在运筹学中,通常将优化问题分为线性优化问题和非线性优化问题两种。
1. 线性优化问题线性优化问题的目标函数和约束条件都是线性的,即可以表示为一次函数的形式。
线性优化问题有着广泛的应用,如生产计划、资源分配等。
常见的线性优化问题包括线性规划、整数规划和网络流问题等。
2. 非线性优化问题非线性优化问题的目标函数和约束条件中存在非线性项,求解非线性优化问题通常比较复杂。
非线性优化问题的应用领域包括经济学、工程学、生物学等。
常见的非线性优化问题有最优化、最优控制等。
二、决策分析的基本概念决策分析是指通过对问题的分析和评估,选择出符合实际需要且最有利于实现目标的决策方案。
决策分析的核心在于确定决策变量、评估目标和制定约束条件。
1. 决策变量决策变量是指在决策分析中可以被调整的变量,通过调整决策变量可以影响决策方案的结果。
决策变量的选择对于决策分析的准确性和有效性至关重要。
2. 评估目标评估目标是对决策方案进行衡量和比较的标准。
在决策分析中,常常会涉及到多个评估目标,需要通过综合考虑来确定最终的决策方案。
3. 约束条件约束条件是指决策方案在实施过程中要满足的限制条件。
约束条件可以是资源的限制、技术的要求等,根据具体情况来确定。
三、优化问题与决策分析的关系优化问题和决策分析有着密切的联系。
优化问题可以作为决策分析的一种方法,通过求解优化问题来得到最优的决策方案。
1. 决策变量与优化变量在决策分析中,决策变量是决策方案中可以调整的变量。
而在优化问题中,优化变量即为优化问题中需要确定的变量。
决策变量可以作为优化变量,通过求解优化问题得到最优解,从而得到最优的决策方案。
统计学中的运筹学与决策分析统计学是一门研究数据收集、处理、分析和解释的学科,它在决策制定和问题解决中起着重要的作用。
运筹学和决策分析作为统计学的两个重要分支,通过运用数学和统计学方法,帮助决策者在复杂的环境中做出有效的决策。
本文将探讨统计学中的运筹学和决策分析,并介绍它们在实践中的应用。
运筹学在统计学中占据重要地位。
它是一种利用数学和统计学方法来研究最优化问题的科学。
最优化问题是指如何在给定的约束条件下,找到使目标函数取得最优值的决策变量值。
例如,在生产过程中如何最大化产量或最小化成本,都是典型的最优化问题。
运筹学能够通过建立数学模型,使用数学规划和优化算法,找到最优解决方案,并为决策者提供决策支持。
决策分析是统计学中另一个重要的分支。
它是一种研究决策制定过程的科学方法。
决策分析的核心是分析决策问题的各种可能性和风险,并评估各种决策方案的效果。
决策分析使用统计推断、风险分析和决策树等方法,帮助决策者在不确定性条件下做出最佳的决策。
例如,在投资决策中,决策分析可以帮助投资者评估不同投资方案的风险和回报,选择最优的投资策略。
在实践中,运筹学和决策分析广泛应用于各个领域。
在物流管理中,运筹学可以优化物流网络的设计,降低物流成本;在供应链管理中,运筹学可以优化供应链的运作,提高物流效率。
在金融行业中,决策分析可以帮助投资者制定投资策略,降低风险;在医疗领域中,决策分析可以帮助医生评估不同治疗方案的效果,制定最佳的治疗计划。
除此之外,运筹学和决策分析还在交通规划、环境管理、能源优化等领域发挥着重要作用。
它们的应用不仅可以提高效率,降低成本,还可以提高决策的准确性和可靠性,帮助组织和个人做出明智的决策。
总之,统计学中的运筹学和决策分析是一门理论与实践相结合的学科,在各个领域中都具有重要的应用价值。
运筹学帮助我们找到最优解决方案,决策分析帮助我们做出最佳决策。
通过运用数学和统计学的方法,它们可以为决策者提供科学的决策支持,推动各个领域的发展。
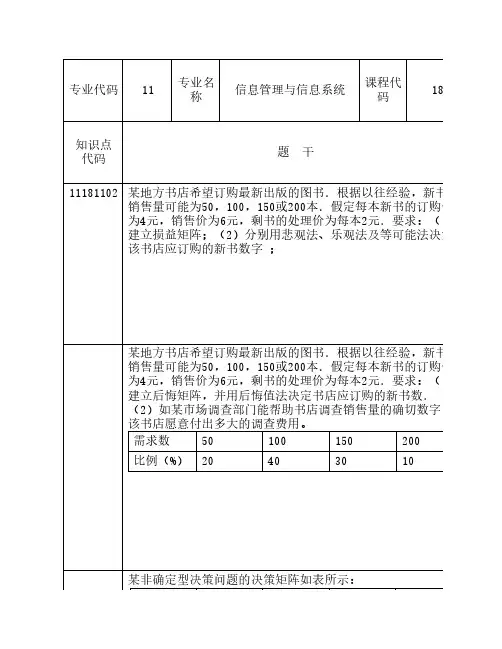
决策分析复习资料决策分析复习资料第1题:管理科学(Management science)是对与定量因素(quantitative factors)有关的管理问题通过应用科学的方法(scientific approach)进行辅助管理决策制定(aid managerial decision making)的一门学科(discipline)。
对第2题:在随机型决策问题,也就是存在不确定性的决策问题中,决策人可以在各种可能的行动中进行选择;但是有些因素是决策人所无法控制的。
我们把决策问题中决策人无法控制的所有因素,即凡是能够引起决策问题的不确定性的因素,统称作自然状态。
(对)第3题:决策理论是(ABCD )A. 运筹学的一支B. 是经济学和管理科学的重要组成部分C. 是控制论的延伸D. 是社会科学与自然科学的交叉,是典型的软科学第4题:由于经济学家、数学家以及系统科学家的努力,决策分析日益广泛地应用于商业、经济、实用统计、法律、医学、政治等各方面。
(对)第5题:满足以下哪几个条件的决策属于不确定型决策( ABCD)A.存在着一个明确的决策目标 B. 存在着两个或两个以上随机的自然状态C. 存在着可供决策者选择的两个或两个以上的行动方案D. 可求得各方案在各状态下的益损矩阵 E. 能获得各个自然状态发生的概率第6题:标准损失函数有以下哪几种?(ABC)A. 平方损失B. 线性损失C. 0-1损失D. 对数损失第7题:以下(ABCDE)项属于决策的要素A.决策者 B. 分析者 C. 目标 D. 行动空间 E. 结果空间第8题:在下雨带伞问题中的下不下雨是自然状态,在购买火灾保险中的是否发生火灾是自然状态。
(对)第9题:匹兹堡开发公司(PDC)已购得一块地用于建造一个高档的沿河综合商业楼,其位置对繁华的匹兹堡和金三角有很好的景观,所谓金三角是指两条小河汇流成俄亥俄(Ohio)河的地段。
每一个建筑物单元的价格是30万~120万,取决于单元所处楼层、面积以及备选的设施。
运筹学知识点总结归纳运筹学知识点总结归纳一、引言运筹学是一门综合运用数学、统计学和优化理论等相关知识解决实际问题的学科。
它的一个核心目标是在给定的约束条件下,使系统达到最佳状态。
本文将对运筹学的一些基本概念、方法和应用进行总结归纳,以便读者对这门学科有更深入的了解。
二、线性规划线性规划是运筹学中最基本、最常见的数学模型之一。
在线性规划中,目标函数和约束条件都是线性的。
通过线性规划,我们可以最小化或最大化一个目标函数来寻找最优解。
常见的线性规划方法有单纯形法、对偶法和内点法等。
三、整数规划整数规划是线性规划的一种扩展形式。
在整数规划中,决策变量的取值限制为整数。
这种限制使问题更加复杂,通常需要使用分支定界法、割平面法等算法来求解。
整数规划在许多实际问题中有广泛的应用,如生产调度、路径优化等。
四、网络流问题网络流问题是运筹学中一个重要的研究方向。
在网络流问题中,节点和边表示物理或逻辑上的位置,流量沿边流动,目标是最大化总流量或最小化总成本。
常见的网络流问题有最小费用流问题、最大流问题等。
在实际应用中,网络流问题可以用于交通规划、供应链管理等领域。
五、排队论排队论是研究队列系统的数学理论。
队列是指一组按照某种顺序排列的实体,而排队论则是研究这些实体如何进入和离开队列的过程。
通过排队论,可以估计系统的性能指标,如平均等待时间、系统利用率等。
排队论在交通管理、生产调度等领域有广泛的应用。
六、决策分析决策分析是运筹学中的一个重要分支,旨在通过分析问题的数据和信息,寻找最优的决策方案。
决策分析中常用的工具包括决策树分析、多属性决策等。
通过决策分析,我们可以对风险进行评估,并为决策者提供有力的支持。
七、多目标规划多目标规划是一种同时优化多个目标函数的决策问题。
在多目标规划中,不同的目标可能相互冲突,无法简单地将其转化为单一目标。
解决多目标规划问题的方法有权重法、向量法等。
多目标规划在工程设计、投资组合等领域有广泛的应用。