UG关于连续的几种方式
- 格式:doc
- 大小:251.00 KB
- 文档页数:5

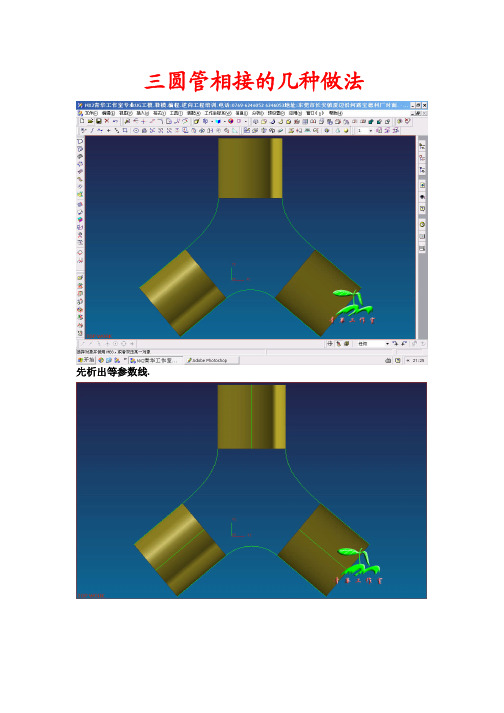
三圆管相接的几种做法
先析出等参数线.
把析出的线延长后桥接如图.
网格出各个面.
在中间三角线处画出一个四边形,四边形大于三角形线的每个外点,拉伸后裁剪如图
网格面,别忘了相切四边.
分析图.
第二种做法
析出线,数量为设为7
做出两边的面,如图
两点画线,并把参数设为无限制.如图.
投影并做出红色线.注意,红色线的调节,高度不能超过圆的最高点.且要相切两边线.
从前面看一下线的调节.我用上面圆的最高线来控制.
网格面,记得在做网格面时一定要选中间的线来做控制.
再桥接出第三边线,投影后裁剪,做网格面.
面分析图.
第三种做法桥接出线
做出网格面.用桥接也可以,但必须指定线.大家可以试试就知道了.
析出面的中线,并把顶部面的中线延长至红色线.
过三点做弧,并投影至面.如图红色线.
裁剪后,网格面.
分析图.。

关于连续的几种方式,以下是我个人的一点看法:G0连续又叫——点连续。
是指曲线或曲面与任意平面交线是连续曲线,没有断点,既曲线方程连续。
对曲面来说,说白了就是没有裂缝。
G1连续又叫——相切连续。
是指曲线或曲面与任意平面交线平滑无折点(相切),既曲线方程一阶导数连续。
对曲面来说,说白了就是处处圆滑相切,没有楞,显示曲率时颜色有突变。
G2连续又叫——曲率连续。
是指曲线或曲面与任意平面交线的各点曲率连续,作曲率分析的曲线是连续曲线,无断点。
既曲线方程一阶导数曲线平滑,二阶导数曲线连续。
对曲面,最简单的判断方法就是斑马线圆滑无折点,显示曲率时颜色是渐变的。
G3连续又叫——?(我的叫它曲率变化连续)。
是指曲线或曲面与任意平面交线的各点曲率变化率连续,作曲率分析的曲线是平滑曲线,无折点。
既曲线方程一阶导数曲线平滑,二阶导数曲线平滑,三阶导数曲线连续。
小弟才疏学浅,除了用曲率分析外不知其他的判断方法,请各位大侠指教。
由上,我个人拙见:所谓G1、G2、G3是指曲线方程最高导数曲线连续的阶次,例如G2连续曲线1、2阶导数曲线都连续。
好像记得高等数学有这样一个定理:如果一个曲线方程一阶、二阶、三阶导数连续,则其n阶导数曲线连续(n为自然数)。
我想这也许是将G3连续称作完美曲线的原因吧,也许也是没有什么G4、G5连续的原因。
严重声明:本人是菜鸟一个,以上只是个人在这个论坛混了几个月的一点思考。
肯定有错误,请大侠不吝指教,我尽快改正,以免扰己误人。
另:本人作图说明各种连续,但是没有更简单明确的方式说明G3连续,请大侠门帮忙赐我一个例子。
各种连续的曲线说明:以下是简单曲面的说明:以下是班马线说明:曲面曲率分析说明:。

曲线绘图的连续性简介G0——点连续:是指曲面或曲线点点连续。
曲线无断点,曲面相接处无裂缝。
判定方法:曲线不断,但是有角;曲面没有窟窿或裂缝,但是有楞。
数学解释:曲线或任意平面与该曲面的交线处处连续。
G1——相切连续:是指曲面或曲线点点连续,并且所有连接的线段、曲面片之间都是相切关系。
判定方法:曲线不断,平滑无尖角;曲面连续,没有楞角。
数学解释:曲线或任意平面与该曲面的交线处处连续,且一阶导数连续。
G2——曲率连续:是指曲面或曲线点点连续,并且其曲率分析结果为连续变化。
判定方法:对曲线做曲率分析,曲率曲线连续无断点。
对平面做斑马线分析,所有斑马线平滑,没有尖角。
数学解释:曲线或任意平面与该曲面的交线处处连续,且二阶导数连续。
G3——曲率相切连续:是指曲面或曲线点点连续,并且其曲率曲线或曲率曲面分析结果为相切连续。
判定方法:对曲线做曲率分析,曲率曲线连续,且平滑无尖角。
因为对G3连续用到的比较少,目前还不知道什么更好的G3曲面判定方法,请高手补充。
数学解释:曲线或任意平面与该曲面的交线处处连续,且三阶导数连续。
9、Gn连续的定义1、Gn表示两个几何对象间的实际连续程度。
G0两个对象相连或两个对象的位置是连续的。
G0连续(也称为点连续)在每个表面上产生一次反射,这种连续仅仅保证曲面间没有缝隙而是完全接触。
G1两个对象光顺连续,一阶微分连续,或者是相切连续的。
G1连续(也称为切线连续)将产生一次完整的表面反射,反射线连续但是扭曲状,这种连续仅是方向的连续而没有半径连续。
我们通常的倒圆角就是这种情况。
G2两个对象光顺连续,二阶微分连续,或者两个对象的曲率是连续的。
G2连续(也称为曲率连续)将产生横过所以边界的完整的和光滑的反射纹。
曲率连续意味着在任何曲面上的任一"点"中沿着边界有相同的曲率半径。
外观质量要求高的产品需要曲率做到G2连续,其实曲面做到这一点难度是很大发。
在我们一般的产品设计中G1连续就能满足大部分产品开发需要。

1 / 4曲线绘图的连续性简介G0——点连续:是指曲面或曲线点点连续。
曲线无断点,曲面相接处无裂缝。
判定方法:曲线不断,但是有角;曲面没有窟窿或裂缝,但是有楞。
数学解释:曲线或任意平面与该曲面的交线处处连续。
G1——相切连续:是指曲面或曲线点点连续,并且所有连接的线段、曲面片之间都是相切关系。
判定方法:曲线不断,平滑无尖角;曲面连续,没有楞角。
数学解释:曲线或任意平面与该曲面的交线处处连续,且一阶导数连续。
G2——曲率连续:是指曲面或曲线点点连续,并且其曲率分析结果为连续变化。
判定方法:对曲线做曲率分析,曲率曲线连续无断点。
对平面做斑马线分析,所有斑马线平滑,没有尖角。
数学解释:曲线或任意平面与该曲面的交线处处连续,且二阶导数连续。
2 / 4G3——曲率相切连续:是指曲面或曲线点点连续,并且其曲率曲线或曲率曲面分析结果为相切连续。
判定方法:对曲线做曲率分析,曲率曲线连续,且平滑无尖角。
因为对G3连续用到的比较少,目前还不知道什么更好的G3曲面判定方法,请高手补充。
数学解释:曲线或任意平面与该曲面的交线处处连续,且三阶导数连续。
9、Gn连续的定义1、Gn表示两个几何对象间的实际连续程度。
G0两个对象相连或两个对象的位置是连续的。
G0连续(也称为点连续)在每个表面上产生一次反射,这种连续仅仅保证曲面间没有缝隙而是完全接触。
G1两个对象光顺连续,一阶微分连续,或者是相切连续的。
G1连续(也称为切线连续)将产生一次完整的表面反射,反射线连续但是扭曲状,这种连续仅是方向的连续而没有半径连续。
我们通常的倒圆角就是这种情况。
G2两个对象光顺连续,二阶微分连续,或者两个对象的曲率是连续的。
G2连续(也称为曲率连续)将产生横过所以边界的完整的和光滑的反射纹。
曲率连续意味着在任何曲面上的任一点中沿着边界有相同的曲率半径。
外观质量要求高的产品需要曲率做到G2连续,其实曲面做到这一点难度是很大发。
在我们一般的产品设计中G1连续就能满足大部分产品开发需要。

UG基础与实用技巧大家有好的技巧可以拿出来分享一下!1。
旋转: MB22。
平移: SHIFT+MB2 或者 MB2 + MB33。
缩放: CTRL +MB2 或者 MB2 + MB14。
当平移工作坐标系时通过向下按住ALT键,你可以执行精确定位。
5。
制图中,你可以在线性尺寸上用SHIFT-拖动来创建狭窄型尺寸。
6。
您可以双击在资源条中的导航器或调色板标签,以使它们跳出去并可单独放置。
7。
当作草图时,点线显示与其它对象对齐,虚线显示可能的约束。
使用 MB2 来锁定所建议的约束。
8。
在制图中 - 没有活动的对话框时,您可以拖动尺寸来移动其原点并自动判断其指引线侧。
9。
您可以按住 MB2 并拖动来旋转视图。
使用 Shift+MB2 (或 MB2+MB3)来平移。
使用Ctrl+MB1 (或 MB1+MB2) 来放大/缩小。
甚至滑轨式鼠标都可用来缩放!10。
在草图轮廓,您可以通过按/拖 MB1 来从画直线切换到划弧。
移动光标通过各象限来获取所需要的弧。
11。
在制图中,您可以在线性尺寸上用 Shift-拖动来创建狭窄型尺寸。
12。
可以在任何时候双击动态工作坐标系来将其激活!一旦被激活,您可以使用捕捉点来拖动原点,或者您可以沿轴方向来拖动,或者您可以旋转。
您也可以双击一条轴使方向逆反。
13。
在草图约束中,在选择要约束的曲线之后,系统将显示可用约束的列表。
已经应用的约束将显示为灰色。
您还可以从 MB3 弹出菜单上选择约束。
14。
在制图中,动画图纸创建可以通过将先前生成的图纸模板拖动到资源条的模型中来获得。
15。
您可以选择将资源条放在屏幕一侧 - 左侧或右侧。
到预设置->用户界面-资源条来改变它。
16。
在草图约束,在应用约束之后使用 Ctrl-MB1 以保持选择了的对象。
这允许您很容易地应用多个约束,例如:平行和等长度同时使用。
17。
在制图中,双击任何尺寸或注释来编辑其内容。
您也可以从 MB3 弹出菜单来选择其它操作。
120种UG表达式曲线画法(阿基米德螺旋线、数学方程式)在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线:1、极坐标(或柱坐标r,θ,z)与直角坐标系(x,y,z)的转换关系:x=r*cos(θ);y=r*sin(θ);z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ;y=rsin θsinφ;z=rcosθ在UG表达式中输入的theta=θ;phi=φ;r=rho【注:所有UG表达式中,必须先在名称栏输入t,公式栏输入0,类型为恒定的,即无单位。
t是UG自带的系统变量,其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0),若直线经过点(10,20),倾角θ为30°,长度L为40,即UG表达式为:theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1 2.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2,若圆心坐标为(50,40),半径r为30,即UG表达式为:r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1,若椭圆中心坐标为(50,40),长半轴a为30(在X轴上),短半轴b为20,即UG表达式为:a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图34.双曲线双曲线的数学方程为x2/a2-y2/b2=1,若中心坐标为(0,0),实长半轴a为4(在x轴上),虚半轴b为3,y的取值范围为-5~+5内的一段,即UG表达式为:a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制,效果如图45.抛物线抛物线I的数学方程为y2=2px,若抛物线的顶点为(30,20)焦点到准线的距离p=8,y的取值范围为-25~+25,即UG表达式为:p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程:x=2pt2,y=2pt(其中t为参数)。
ug桥接曲线讲解
UG是一款强大的三维CAD设计软件,其桥接曲线功能是用来连接两条不
同或相同的曲线,使之成为一条连续的曲线。
使用这个功能可以在创建复杂形状或对现有形状进行修改时,非常方便地连接不同的曲线段。
使用UG的桥接曲线功能,需要遵循以下步骤:
1. 打开UG软件并打开需要编辑的文件。
2. 在建模环境中,选择“插入”菜单,然后选择“派生曲线”子菜单,最后选择“桥接”命令。
3. 在弹出的“桥接”对话框中,选择需要连接的第一条曲线,即起始对象。
4. 根据需要选择不同的桥接类型,如“简单”、“通过点”或“二次曲线”。
每种类型都有不同的参数设置。
5. 根据需要设置其他参数,如连续性、位置、方向等。
这些参数控制桥接曲线的形状和位置。
6. 选择需要连接的第二条曲线,即终止对象。
7. 点击“确定”按钮,UG会自动计算并生成桥接曲线。
8. 可以使用其他工具对生成的桥接曲线进行编辑和修改,以确保其符合设计要求。
需要注意的是,UG的桥接曲线功能非常强大,可以创建各种复杂的桥接曲线。
但同时也需要具备一定的UG基础知识和对曲线形状的控制能力,以便更好地应用该功能。
UG2.0版本* 图层1、分为1~256层,每层图素都可以是三维的。
只有一个图层是工作层,其他可以设置为可见性、隐藏和可选择性。
2、可以复制和移动层和层之间的选项。
* 矢量构造器就是有方向的向量,及一带方向的直线。
* 类选择器1、可以选择一类的元素;2、可以通过层选择;3、可以反向选择。
* UG启动可以从开始菜单或者安装目录或者从桌面快捷方式。
注:建立桌面快捷方式是要从安装目录中发送桌面快捷方式才可以,从开始菜单中发送是不可以启动的。
* 部件导航器(可以固定或者活动)1、装配导航器2、部件导航器:可以单独操作某个特征,如删除一个R角。
3、历史导航器:过去时间打开的部件,可以在上面用缩略图、列表、平铺等。
注:文件—打开也有打开的文件,但那只是显示8个文件。
* 键盘的用法1、所有的快捷键在:信息—自定义菜单2、可以用ALT+菜单命令后面的热键字母启动用快捷键。
3、可以用“+-*/”直接输入数字,UG会自动计算,如10+10+10、8/6等。
4、常用的快捷键如下:CTRL+M 建模CTRL+O 打开CTRL+N 新建CTRL+S 保存CTRL+B 隐藏CTRL+SHIFT+U 显示所有的CTRL+SHIFT+B互换显示与隐藏CTRL+T 变换CTRL+ALT+M 加工CTRL+Z 撤销CTRL+C 复制CTRL+X 剪切CTRL+V 粘贴CTRL+L 图层设置CTRL+A 全选CTRL+F 拟合CTRL+J 对象显示CTRL+SHIFT+D 制图* 鼠标的用法1、左键选取,右键弹出快捷菜单。
2、中键确定或者旋转图形(旋转如果随意按住中键则自由旋转,若靠边则绕轴旋转)。
3、CTRL+中键为缩放(左键+中键也为缩放)4、SHIFT+中键为平移(右键+中键也为平移)5、ALT+中键为取消=ESC。
* 信息—点是用来查询点的坐标信息的,与分析距离有区别。
* 隐藏1、快捷键为CTRL+B2、不隐藏所选的意思是把即将要被隐藏的显示出来让其不被隐藏。
关于连续的几种方式,以下是我个人的一点看法:G0连续又叫——点连续。
是指曲线或曲面与任意平面交线是连续曲线,没有断点,既曲线方程连续。
对曲面来说,说白了就是没有裂缝。
G1连续又叫——相切连续。
是指曲线或曲面与任意平面交线平滑无折点(相切),既曲线方程一阶导数连续。
对曲面来说,说白了就是处处圆滑相切,没有楞,显示曲率时颜色有突变。
G2连续又叫——曲率连续。
是指曲线或曲面与任意平面交线的各点曲率连续,作曲率分析的曲线是连续曲线,无断点。
既曲线方程一阶导数曲线平滑,二阶导数曲线连续。
对曲面,最简单的判断方法就是斑马线圆滑无折点,显示曲率时颜色是渐变的。
G3连续又叫——?(我的叫它曲率变化连续)。
是指曲线或曲面与任意平面交线的各点曲率变化率连续,作曲率分析的曲线是平滑曲线,无折点。
既曲线方程一阶导数曲线平滑,二阶导数曲线平滑,三阶导数曲线连续。
小弟才疏学浅,除了用曲率分析外不知其他的判断方法,请各位大侠指教。
由上,我个人拙见:所谓G1、G2、G3是指曲线方程最高导数曲线连续的阶次,例如G2连续曲线1、2阶导数曲线都连续。
好像记得高等数学有这样一个定理:如果一个曲线方程一阶、二阶、三阶导数连续,则其n阶导数曲线连续(n为自然数)。
我想这也许是将G3连续称作完美曲线的原因吧,也许也是没有什么G4、G5连续的原因。
严重声明:本人是菜鸟一个,以上只是个人在这个论坛混了几个月的一点思考。
肯定有错误,请大侠不吝指教,我尽快改正,以免扰己误人。
另:本人作图说明各种连续,但是没有更简单明确的方式说明G3连续,请大侠门帮忙赐我一个例子。
各种连续的曲线说明:以下是简单曲面的说明:以下是班马线说明:曲面曲率分析说明:。
关于连续的几种方式,以下是我个人的一点看法:
G0连续又叫——点连续。
是指曲线或曲面与任意平面交线是连续曲线,没有断点,既曲线方程连续。
对曲面来说,说白了就是没有裂缝。
G1连续又叫——相切连续。
是指曲线或曲面与任意平面交线平滑无折点(相切),既曲线方程一阶导数连续。
对曲面来说,说白了就是处处圆滑相切,没有楞,显示曲率时颜色有突变。
G2连续又叫——曲率连续。
是指曲线或曲面与任意平面交线的各点曲率连续,作曲率分析的曲线是连续曲线,无断点。
既曲线方程一阶导数曲线平滑,二阶导数曲线连续。
对曲面,最简单的判断方法就是斑马线圆滑无折点,显示曲率时颜色是渐变的。
G3连续又叫——?(我的叫它曲率变化连续)。
是指曲线或曲面与任意平面交线的各点曲率变化率连续,作曲率分析的曲线是平滑曲线,无折点。
既曲线方程一阶导数曲线平滑,二阶导数曲线平滑,三阶导数曲线连续。
小弟才疏学浅,除了用曲率分析外不知其他的判断方法,请各位大侠指教。
由上,我个人拙见:所谓G1、G2、G3是指曲线方程最高导数曲线连续的阶次,例如G2连续曲线1、2阶导数曲线都连续。
好像记得高等数学有这样一个定理:如果一个曲线方程一阶、二阶、三阶导数连续,则其n阶导数曲线连续(n为自然数)。
我想这也许是将G3连续称作完美曲线的原因吧,也许也是没有什么G4、G5连续的原因。
严重声明:本人是菜鸟一个,以上只是个人在这个论坛混了几个月的一点思考。
肯定有错误,请大侠不吝指教,我尽快改正,以免扰己误人。
另:本人作图说明各种连续,但是没有更简单明确的方式说明G3连续,请大侠门帮忙赐我一个例子。
各种连续的曲线说明:
以下是简单曲面的说明:
以下是班马线说明:
曲面曲率分析说明:。