下载文档原格式
计算机控制技术练习题（附答案）一、填空题（每空2分，共20分）1．闭环负反馈控制的基本特征是。
2．闭环控制系统里，不同输出与输入之间的传递函数分母。
3．惯性环节的主要特点是，当其输入量发生突然变化时，其输出量不能突变，而是按变化。
4．静态误差系数是系统在典型外作用下精度的指标，静态误差系数越大，精度。
5．系统的相稳定裕度γM，定义为开环频率特性在截止频率ωc处。
6．离散系统稳定性与连续系统不同，它不仅与系统结构和参数有关，还与系统的有关。
7．零阶保持器是一个相位滞后环节，它的相频特性φ(ω)= 。
8．若已知闭环系统自然频率为ωn，经验上，采样频率ωs应取。
9．通常把叠加在被测信号上的干扰信号称为。
10．为使传感器特性与A/D变换器特性相匹配，通常应在传感器与A/D之间加入。
二、选择题(每题2分，共10分)1．在计算机控制系统里，通常当采样周期T减少时，由于字长有限所引起的量化误差将。
A 增大；B 减小；C 不变。
2．控制算法直接编排实现与串联编排实现相比，有限字长所引起的量化误差。
A 较大；B 较小；C 相当。
3．某系统的Z传递函数为G(z) = 0.5(z+0.5) / (z+1.2)(z-0.5) ，可知该系统是。
A稳定的；B不稳定的；C 临界稳定的。
4．若以电机轴的转角为输入量，电机轴的转速为输出量，则它的传递函数为环节。
A 积分；B 微分；C 惯性。
5．在确定A/D变换器精度时，通常要求它的精度应传感器的精度。
A 大于；B 小于；C 等于。
三、简答题（每小题5分，共20分）1．图1为水箱水位自动控制系统，试说明基本工作原理。
图12．已知单位负反馈闭环控制系统的单位阶跃响应的稳态误差为0.1，试问该系统为几型系统，系统的开环放大系数为多少?3．试简单说明系统稳定性与稳态误差相互矛盾的关系。
4．试表述采样定理，并说明若一高频信号采样时不满足采样定理，采样后将会变成何种信号。
四、（10分）已知单位负反馈系统开环传递函数为G(s)=ωn 2/s(s+2ζωn )实测求得单位阶跃响应的σ%=4.3%，t s =2.5秒，试写出闭环传递函数并求ωn ，ζ为多少。
离散控制与连续控制的比较与分析离散控制与连续控制是自动控制领域中两种不同的控制方法。
离散控制适用于那些以离散事件为基础的系统，而连续控制则适用于那些以连续参数为基础的系统。
本文将对离散控制与连续控制进行比较与分析。
一、基本概念离散控制：离散控制是一种以时间为基础的控制方法，它依靠离散事件的发生来触发控制动作。
在离散控制中，系统的状态在不同的时间点上以离散的方式进行变化。
连续控制：连续控制是一种以连续参数的变化为基础的控制方法，它依靠系统的连续性状态来实时调整控制器的输出值。
在连续控制中，系统的状态在任意时间点上以连续的方式进行变化。
二、控制器设计离散控制：离散控制通常使用离散控制算法，如PID控制算法。
这些算法将采样时间作为基准，通过对离散数据进行处理来确定控制器的输出值。
离散控制器的设计相对简单，容易实现。
连续控制：连续控制通常使用连续控制算法，如模糊控制、神经网络控制等。
这些算法通过对系统状态的连续监测，实时调整控制器的输出值。
连续控制器的设计复杂度高，需要考虑系统的动力学特性等因素。
三、响应速度离散控制：离散控制的响应速度相对较慢，因为其控制动作是通过离散事件的发生来触发的。
离散控制器在两个采样点之间的时间段内，无法对系统状态进行控制。
连续控制：连续控制的响应速度相对较快，因为其控制动作是实时调整的。
连续控制器可以在任意时间点上对系统状态进行控制，能够快速响应系统的变化。
四、系统稳定性离散控制：离散控制系统相对容易保持稳定，因为其控制动作是基于对离散数据的处理。
离散控制器可以通过调整采样周期来实现系统的稳定性。
连续控制：连续控制系统相对较难保持稳定，因为其控制动作是基于对连续参数的调整。
连续控制器需要考虑系统的动力学特性以及噪声等因素，以保证系统的稳定性。
五、应用领域离散控制：离散控制适用于那些以离散事件为基础的系统，如自动化生产线、数字电子设备等。
离散控制在许多工业领域中得到广泛应用。
连续控制：连续控制适用于那些以连续参数为基础的系统，如化工过程、机械控制系统等。
自动控制原理离散系统知识点总结自动控制原理中的离散系统是指在时间域和数值范围上都是离散的系统。
在离散系统中，信号是以离散时间点的形式传递和处理的。
本文将对自动控制原理离散系统的知识点进行总结，包括离散系统的概念、离散信号与离散系统的数学表示、离散系统的稳定性分析与设计等。
一、离散系统的概念与特点离散系统是指系统输入、输出和状态在时间上都是以离散的方式存在的系统。
与连续系统相比，离散系统具有以下特点：1. 离散时间：离散系统的输入、输出和状态是在离散时间点上采样得到的，而不是连续的时间信号。
2. 离散数值：离散系统的输入、输出和状态都是以离散数值的形式存在的，而不是连续的模拟数值。
二、离散信号与离散系统的数学表示离散信号是指在离散时间点上采样得到的信号。
离散系统可以通过离散信号的输入与输出之间的关系进行描述。
常见的离散系统数学表示方法有差分方程和离散时间传递函数。
1. 差分方程表示：差分方程是通过离散时间点上的输入信号和输出信号之间的关系来描述离散系统的。
差分方程可以是线性的或非线性的，可以是时不变的或时变的。
2. 离散时间传递函数表示：离散时间传递函数描述了离散系统输入与输出之间的关系，类似于连续时间传递函数。
离散时间传递函数可以通过Z变换得到。
三、离散系统的稳定性分析与设计离散系统的稳定性是指系统的输出在有限时间内收敛到有限范围内，而不是无限增长或震荡。
离散系统的稳定性分析与设计是自动控制原理中的重要内容。
1. 稳定性分析：离散系统的稳定性可以通过判断系统的极点位置来进行分析。
若系统的所有极点都位于单位圆内，则系统是稳定的；若存在至少一个极点位于单位圆外，则系统是不稳定的。
2. 稳定性设计：若离散系统不稳定，可以通过调整系统的参数或设计控制器来实现稳定性。
常见的稳定性设计方法包括PID控制器调整、根轨迹设计等。
四、离散系统的性能指标与优化离散系统的性能指标与优化是指通过调整控制器参数或控制策略，使离散系统的性能得到优化。
控制系统数字仿真题库一、填空题1. 定义一个系统时，首先要确定系统的边界；边界确定了系统的范围，边界以外对系统的作用称为系统的输入，系统对边界以为环境的作用称为系统的输出。
2．系统的三大要素为：实体、属性和活动。
3．人们描述系统的常见术语为：实体、属性、事件和活动。
4．人们经常把系统分成四类，它们分别为：连续系统、离散系统、采样数据系统和离散-连续系统。
5、根据系统的属性可以将系统分成两大类：工程系统和非工程系统。
6．根据描述方法不同，离散系统可以分为：离散时间系统和离散事件系统。
7. 系统是指相互联系又相互作用的实体的有机组合。
8．根据模型的表达形式，模型可以分为物理模型和数学模型二大类，其中数学模型根据数学表达形式的不同可分为二种，分别为：静态模型和动态模型。
9、采用一定比例按照真实系统的样子制作的模型称为物理模型，用数学表达式来描述系统内在规律的模型称为数学模型。
10．静态模型的数学表达形式一般是代数方程和逻辑关系表达式等，而动态模型的数学表达形式一般是微分方程和差分方程。
11．系统模型根据描述变量的函数关系可以分类为线性模型和非线性模型。
12 仿真模型的校核是指检验数字仿真模型和数学模型是否一致。
13．仿真模型的验证是指检验数字仿真模型和实际系统是否一致。
14．计算机仿真的三个要素为：系统、模型与计算机。
15．系统仿真的三个基本活动是系统建模、仿真建模和仿真试验。
16．系统仿真根据模型种类的不同可分为：物理仿真、数学仿真和数学-物理混合仿真。
17．根据仿真应用目的的不同，人们经常把计算机仿真应用分为四类，分别为：系统分析、系统设计、理论验证和人员训练。
18．计算机仿真是指将模型在计算机上进行实验的过程。
19. 仿真依据的基本原则是:相似原理。
20. 连续系统仿真中常见的一对矛盾为计算速度和计算精度。
21．保持器是一种将离散时间信号恢复成连续信号的装置。
22．零阶保持器能较好地再现阶跃信号。
连续系统与离散系统的概念连续系统和离散系统是系统控制理论中两种基本的模型类型。
连续系统是指系统的输入和输出信号是连续变化的，并且系统的状态可以在任意时间点进行测量和控制。
而离散系统则是指系统的输入和输出信号是离散的，即只在离散的时刻进行测量和控制，而在两个离散时刻之间的信号变化是未知的。
首先，我们来详细介绍连续系统。
连续系统可以用微分方程来描述，通常采用微分方程的求解方法来求得系统的时域响应。
连续系统可以是线性的，也可以是非线性的。
线性连续系统的特点是具有叠加性质，即输入的线性组合对应于输出的线性组合。
而非线性连续系统则是具有非线性性质，输入的线性组合对应于输出的非线性组合。
连续系统的状态可以通过求解微分方程来得到，并且可以通过选择系统的控制输入来实现对系统状态的调节。
在连续系统中，我们可以利用传递函数来描述系统的频域特性，传递函数是输入和输出的拉普拉斯变换的比值。
传递函数可以用来分析系统的稳定性、频率响应、阻尼特性等。
接下来，我们来介绍离散系统。
离散系统可以用差分方程来描述，通过求解差分方程可以得到系统的时域响应。
离散系统也可以是线性的或非线性的，线性离散系统满足叠加性质，非线性离散系统则不满足叠加性质。
离散系统的状态可以通过迭代差分方程来得到，并且可以通过选择系统的控制输入来实现对系统状态的调节。
离散系统的频域特性可以用离散时间傅里叶变换（DTFT）或离散傅里叶变换（DFT）来描述，这些变换可以将系统的输入和输出信号从时域转换到频域。
离散系统的稳定性、频率响应等也可以通过这些变换来进行分析。
在实际应用中，连续系统和离散系统都有各自的优缺点。
连续系统具有高精度和高灵敏度的特点，适用于需要高精度控制和测量的应用，如机器人控制、飞行器导航等。
而离散系统则具有较低的复杂度和较好的实时性，适合于计算机控制、数字信号处理等应用。
此外，由于实际系统中往往存在传感器采样和控制执行的离散性，所以很多情况下需要将连续系统进行离散化，从而使用离散系统进行建模和控制。
matlab/simulink/simpowersystem中连续vs离散!1.连续系统vs离散系统连续系统是指系统状态的改变在时间上是连续的，从数学建模的角度来看，可以分为连续时间模型、离散时间模型、混合时间模型。
其实在simpowersystem 的库中基本所有模型都属于连续系统，因为其对应的物理世界一般是电机、电源、电力电子器件等等。
离散系统是指系统状态的改变只发生在某些时间点上，而且往往是随机的，比如说某一路口一天的人流量，对离散模型的计算机仿真没有实际意义，只有统计学上的意义，所以在simpowersystem中是没有模型属于离散系统的。
但是在选取模型，以及仿真算法的选择时，常常提到的discrete model、discrete solver、discrete simulate type等等中的离散到底是指什么呢？其实它是指时间上的离散，也就是指离散时间模型。
下文中提到的连续就是指时间上的连续，连续模型就是指连续时间模型。
离散就是指时间上的离散，离散模型就是指离散时间模型，而在物理世界中他们都同属于连续系统。
为什么要将一个连续模型离散化呢？主要是是从系统的数学模型来考虑的，前者是用微分方程来建模的，而后者是用差分方程来建模的，并且差分方程更适合计算机计算，并且前者的仿真算法（simulationsolver）用的是数值积分的方法，而后者则是采用差分方程的状态更新离散算法。
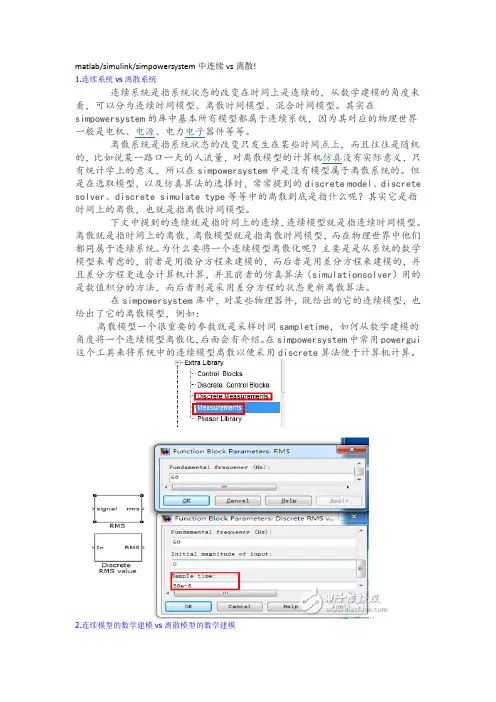
在simpowersystem库中，对某些物理器件，既给出的它的连续模型，也给出了它的离散模型，例如：离散模型一个很重要的参数就是采样时间sampletime，如何从数学建模的角度将一个连续模型离散化，后面会有介绍。
在simpowersystem中常用powergui这个工具来将系统中的连续模型离散以便采用discrete算法便于计算机计算。
2.连续模型的数学建模vs离散模型的数学建模Note：这里的连续和离散都是指时间上的连续和离散，无关乎现实世界的连续系统和离散系统。
离散系统与连续时间系统的根本差别是：离散系统（图3）有采样开关存在，而连续系统则无。
连续信号经过采样开关变成离散信号（图4），采样开关起这理想脉冲发生器的作用，通过它将连续信号调制成脉冲序列。
图3 离散系统方块图图4 离散型时间函数调制之后的信号中，包含与脉冲频率相关的高频频谱（图5），相邻两频谱不相重叠的条件是：max 2f f s其中：s f ---采样开关的采样频率 m ax f ---连续信号频谱中的最高频率这就是采样定理，通常选择采样频率时取四倍连续信号的最大频率。
实验中，信号源产生频率可调的周期性信号，计算机通过A/D 板将信号采集入内存，通过软件示波器显示出来，调整采样频率，可以得到不同的采样结果，以波形图直观显示出来。
由此，可考察波形失真程度。
三、实验使用的仪器设备及实验装置1. 装有LabVIEW 软件和PCI-1200数据采集卡的计算机一台2. 频率计或信号发生器一台3. 外接端子板、数据采集板、计算机、组态软件基于LabVIEW 的信号测试系统主要包括信号发生器、DAQ 数据采集卡和计算机软件三部分组成。
A/D 数据采集采用NI 公司PCMCIA 接口的PCI-1200型多功能数据采集卡；L abVIEW 7.1软件。
将PCI-1200数据采集卡插到计算机主板上的一个空闲的PCI 插槽中，接好各种附件，其驱动程序就是NI-DAQ 。
附件包括一条50芯的数据线，一个型号为CB-50LP 的转接板，转接板直接与外部信号连接。
图5 信号频谱图四、具体实验步骤（一）通过LabVIEW 进行模拟信号的数据采集1. 安装数据采集卡，根据数据采集卡接线指示（图6）连接线路，并检查测试。
2. 熟悉LabVIEW 软件中与数据采集相关的控件与设置项。
3. 编制DAQ 程序，并调试数据采集组态。
4. 应用该组态软件进行波形数据采集并存储，信号种类设置为正弦波，分别设置信号发生器频率为50，100Hz ，观察并记录波形变化。
离散系统与连续时间系统的根本差别是：离散系统（图3）有采样开关存在，而连续系统则无。
连续信号经过采样开关变成离散信号（图4），采样开关起这理想脉冲发生器的作用，通过它将连续信号调制成脉冲序列。
图3 离散系统方块图图4 离散型时间函数调制之后的信号中，包含与脉冲频率相关的高频频谱（图5），相邻两频谱不相重叠的条件是：max 2f f s其中：s f ---采样开关的采样频率 m ax f ---连续信号频谱中的最高频率这就是采样定理，通常选择采样频率时取四倍连续信号的最大频率。
实验中，信号源产生频率可调的周期性信号，计算机通过A/D 板将信号采集入内存，通过软件示波器显示出来，调整采样频率，可以得到不同的采样结果，以波形图直观显示出来。
由此，可考察波形失真程度。
三、实验使用的仪器设备及实验装置1. 装有LabVIEW 软件和PCI-1200数据采集卡的计算机一台2. 频率计或信号发生器一台3. 外接端子板、数据采集板、计算机、组态软件基于LabVIEW 的信号测试系统主要包括信号发生器、DAQ 数据采集卡和计算机软件三部分组成。
A/D 数据采集采用NI 公司PCMCIA 接口的PCI-1200型多功能数据采集卡；L abVIEW 7.1软件。
将PCI-1200数据采集卡插到计算机主板上的一个空闲的PCI 插槽中，接好各种附件，其驱动程序就是NI-DAQ 。
附件包括一条50芯的数据线，一个型号为CB-50LP 的转接板，转接板直接与外部信号连接。
图5 信号频谱图四、具体实验步骤（一）通过LabVIEW 进行模拟信号的数据采集1. 安装数据采集卡，根据数据采集卡接线指示（图6）连接线路，并检查测试。
2. 熟悉LabVIEW 软件中与数据采集相关的控件与设置项。
3. 编制DAQ 程序，并调试数据采集组态。
4. 应用该组态软件进行波形数据采集并存储，信号种类设置为正弦波，分别设置信号发生器频率为50，100Hz ，观察并记录波形变化。
5. 设置信号种类为方波或锯齿波，重复上述实验。
（二）采样定理验证实验1. 按图8连接线路，并检查测试。
2. 熟悉 GeniDAQ 软件中与数据采集相关的控件与设置项。
3. 编制、调试数据采集组态。
4. 应用该组态软件进行波形数据采集并存储，信号种类设置为正弦波，分别设置信号发生器频率为50，100Hz ，采集频率设置为50、100、150、200、300、500Hz ，观察并记录波形变化，体验采样定理的正确性。
五、实验准备及预习要求1．认真阅读实验指导书，在老师答疑和同学讨论的基础上，完成实验准备任务：1).了解数据采集及其硬件（A/D 变换器和数据采集卡）选择的基本知识； 2).熟悉G 语言编程环境和虚拟仪器的含义； 1. 理解采样定理的意义；2.实验前可以参考的书籍：《现代测试技术与数据处理》、《LabVIEW7.1测试技术与仪器应用》等。
六、实验报告内容及格式1．实验目的2．实验内容3．实验装置4．实验原理（测试实验系统图）5．实验步骤6．实验结果与分析（包括实验数据、处理图形、主要关系式和有关程序）7．思考题解析七、开课教师及联系方式开课教师：刘艳明伍耐明联系方式：82317426“振动测量和轴系动平衡实验”教学实验指导书教学实验编号： 041701-3 （可不填）教学实验名称：振动测量和轴系动平衡实验（中文）Oscillation Measurement and Shafting Inertia Balance （英文）学分/学时：1学分/16学时适用专业：发动机、工程热物理、宇航、气动、汽车专业先修课程和环节：了解振动测量的基本原理；振动传感器（位移，速度，加速度）的工作原理；振动信号的描述；机械振动基本参量的常用测量方法。
一、实验目的1、掌握刚性转子现场动平衡的基本作业；2、掌握有关测量仪器的使用；3、通过实验了解动静法的工程应用。
二、实验内容及基本原理实验内容即是对一多圆盘刚性转子用两平面影响系数法进行动平衡。
工作转速低于最低阶段临界转速的转子称为刚性转子，反之称为柔性转子。
本实验采取一种刚性转子动平衡常用的方法――两平面影响系数法。
该方法无需专用平衡机，只要一般的振动测量，适合在转子工作现场进行平衡作业。
根据理论力学的动静法原理：一匀速旋转的长转子，其连续分布的离心惯性力系可向质图一心C 简化为一个合力（主向量）R 和一个合力偶Mc （主矩），见图一。
如果转子的质心恰在转轴上，且转轴恰好是转子的惯性主轴，则合力R 和合力偶矩Mc 的值均为零，这种情况称转子是平衡的；反之，不满足上述条件的转子是不平衡的。
不平衡转子的轴承与轴颈之间产生交变的作用力和反作用力，可引起轴承座和转轴本身的强烈振动，从而影响机器的工作性能和工作寿命。
刚性转子动平衡的目标是，使离心惯性力的合力和合力偶矩的值趋近于零。
为此，我们可以在转子上任意选定两个截面Ⅰ，Ⅱ――称校正平面，在离轴心一定距离1r ，2r ――称校正半径，与转子上某一参考标记成夹角1θ和1θ处，分别附加一块质量为1m 、2m 重块――称校正质量。
如能使两个质量1m 和2m 的离心惯性力（其大小分别为211m ωr 和222m ωr ，ω为转动角速度）的合力和合力偶正好与原不平衡转子的离心惯性力相平衡，那么就实现了刚性转子的动平衡。
两平面影响系数法的过程如下：1) 在额定的工作转速或任选的平衡转速下，检测原始不平衡引起轴承或轴颈A 、B 在 某方位的振动动量11010V ψ<=V 和22020V ψ<=V ，其中10V 和20V 是振动位移，速度或加速度的幅值，1ψ和2ψ是振动信号对转子上参考标记有关的参考脉冲的相位角。
2) 根据转子的结构，选定年两个校正平面Ⅰ、Ⅱ，并确定校正半径1r 、2r ，现在平面 Ⅰ上加一试重111Q β<=t m ，其中11Q m t =为试重质量，1β为试重相对参考标记的方位角，以顺转向为正。
在相同转速下测量轴承A 、B 的振动量11V 和21V 。
矢量关系见图二a 、b 。
显然，矢量11V ～10V 及21V ～20V 。
为平面Ⅰ上加试重1Q 所引 起的轴承振动的变化，称为试重1Q 的效果矢量。
方位角为零度的单位试重的效果矢量称为影响系数。
因而，我们可以由下面式子求影响系数：1101111Q V V -＝α 1202121Q V V -＝α 3) 取走1Q ，在平面上加试重222Q β<=t m ，22Q m t =为试重质量，2β为试重方 位角。
同样测得轴承A 、B 的振动量12V 和22V ，从而求得效果矢量12V ～10V 和22V ～20V （见图二c 、d ）及影响系数：2101212Q VV -＝α 2202222Q V V -＝α 4) 校正平面Ⅰ、Ⅱ上所需的校正量111P θ<=m 和222P θ<=m ，可通过解矢量方程 组求得：⎩⎨⎧-=+-=+2022212110212111V P P V P P αααα 或⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡20102122211211V V P P αααα 11m P =、22m P =为校正质量，1θ，2θ为校正方向角。
求解矢量方程组最好是使用计算机。
要求自编计算机两平面影响系数法动平衡实用程序。
5） 根据计算结果，在转子上安装校正质量，重新启动转子，如振动已减小到满意程度， 则平衡结束，否则可重复上面步骤，再进行一次修正平衡。
图 二三、实验使用的仪器设备及实验装置测试系统如图三所示。
1、转子系统转子轴上固定有四个圆盘，两端用含油轴承支承。
电动机通过橡胶软管拖动转轴，用自r，远低于转子――轴承系统得固有频率。
耦调压器调节转速。
最高工作转速为4000min2、电涡流位移计及ST－5000A型动平衡仪电涡流位移计包括探头和前置器。
探头前端有一扁型线圈，由前置器提供高频（2MHz）电流。
当它靠近金属导体测量对象时，后者表面产生感应电涡流。
间隙变化，电涡流的强弱随之变化，线圈的供电电流也发生变化，从而再串连于线圈的电容上产生被调制的电压信号，此信号经过前置器的调节、检波、放大，成为在一定范围内与间隙大小成比例的直流或低频交流电压信号。
本实验使用两个电涡流计，分别检测两个轴承座的水平振动位移。
两路位移信号通过切换开关依次馈入动平衡仪，以光电变换器给出的电脉冲为参考，进行同频检测（滤除谐波干扰）和相位比较后，在动平衡仪面板上数显出振动位移的幅值、相位及转速数据。
同频检测前后的振动位移波形，通过电子示波器随时观察。
图三3、精密天平用以测量平衡加重的质量4、用电表用以调整电涡流探头的安装位置（初始间隙）。
四、具体实验步骤1、按图三所示连接测试仪器及传感器。
2、打开平衡仪和示波器电源，预热2分钟。
3、转速传感器杆头调整：适当调整传感头端面与标志块（凹块）之间的距离，同时观察转速显示窗口下方的指示灯以表示绿色“OK”灯亮，红色不亮为最佳位置，绿色灯灭为太远，调整时注意凹块不处在传感器的端面为合适。
4、调整两个电涡流探头的位置，使其前端距离轴承座测量表面约1mm，这时用万用表V，线性范围0～测量前置器的输出，应约为－8.0V，因该电涡流位移的灵敏度为8.0mm2mm。
5、转动调压器旋钮，启动转子，供电电压可从零快速调到120V左右，待转子已启动后，再退回到80V左右，以获得较慢转速。
6、 用调压器慢慢升速。
从动平衡仪上观察转速、振幅、相位度数的变化。
在转速从 2000minr至3000minr之间，选择一比较稳定的转速b n ，并使其稳定不变。
从动平衡仪上分别读出转子原始不平衡引起左（A ）、右（B ）轴承座振动位移的幅值和相位角110V ψ<及220V ψ<。
7、 转速回零。
在平面（号圆盘）上任选方位加一试重1m t 。
记录1m t 的值（用天平测 量，可取其在5～8克），及固定点的相位角（以凹面边缘为准作为参考标记算起。
顺转向为正）。
8、 启动转子，新调到平衡转速b n ，测出Ⅰ平面加重后，两个轴承座振动位移的幅值 和相位角（11V 和21V ）。
9、 转速回零。
在Ⅱ平面（4号圆盘）上任选方位加一试重2m t ，拆除2m t 。
测量记录2m t 的值及其固定方位角2β。
10、 转速重新调到b n 。
测出Ⅱ平面加试重后，两个轴承座振动位移的幅值和相位角（12V 和22V ）。
11、自编程序计算。
12、按11步，求出的平衡质量1m 、2m 及校正相位角1θ、2θ在校正平面Ⅰ，Ⅱ 重新加重。
然后将转速调到b n ，再测量记录两个轴承座振动的幅值和相位角。
13、计算平衡率（即平衡前后振动幅值的差与未平衡振幅值的百分比），如高于80％，实验可结束。
