离散时间系统的分析

实验五　离散时间系统的时域分析一、实验目的：（1)理解离散时间信号的系统及其特性。

(２)对简朴的离散时间系统进行分析,研究其时域特性。

(３）运用ＭＡTL ＡＢ对离散时间系统进行仿真,观测成果,理解其时域特性。

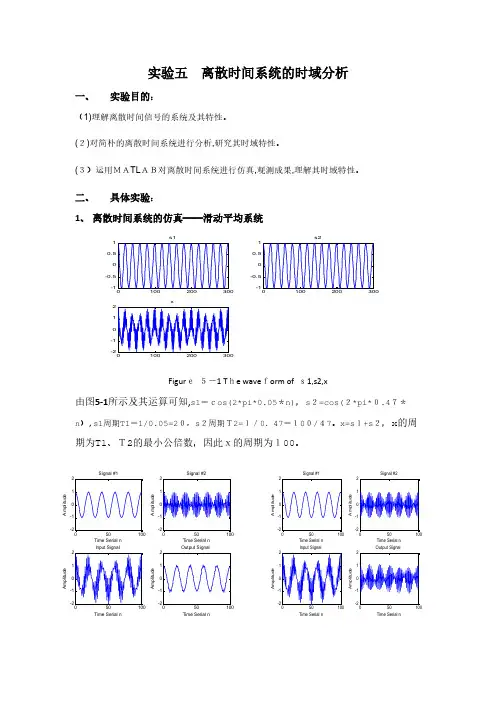
二、具体实验：1、离散时间系统的仿真——滑动平均系统s1s2xFigur ｅ ５－1 T ｈe wave ｆorm of ｓ1,s2,x由图5-1所示及其运算可知,s1＝ｃos(2*pi*0.05＊n)，s ２=cos(２*pi*０.4７＊n ）,s1周期T1＝1/0.05=2０，s ２周期Ｔ2=１／0．47＝１0０/４7。

x=s １+s ２，x 的周期为T1、Ｔ2的最小公倍数，因此ｘ的周期为１00。

Time Serial n A m p l i t u d eSignal #1Time Serial n A m p l i t u d eSignal #2Time Serial nA m p l i t u d eInput SignalTime Serial nA m p l i t u d eOutput SignalTime Serial n A m p l i t u d eSignal #1Time Serial n A m p l i t u d eSignal #2Time Serial nA m p l i t u d eInput SignalTime Serial nA m p l i t u d eOutput SignalF ｉg ｕre 5-2 Fi ｇｕre 5－3（１）如图5-２，当M=2时，第一种图显示的是一种低频信号,第二个是高频信号,第三个图是信号一和信号二的合成的输入，第四个是通过函数Y 的得出的输出。

成果是低频信号，前后对比得出是高频信号被克制了。

本系统是滑动平均滤波器,为低通滤波系统，功能就是从信号中滤除高频分量，因此输入的高频分量s2[n]被该系统克制了。

信号、系统与信号处理实验报告实验一、离散时间系统的时域特性分析姓名:学号:班级：专业：一．实验目的线性时不变（LTI）离散时间系统在时域中可以通过常系数线性差分方程来描述，冲激响应列可以刻画时域特性。

本次实验通过使用MATLAB函数研究离散时间系统的时域特性，以加深对离散时间系统的差分方程、冲激响应和系统的线性和时不变性的理解。

二．基本原理一个离散时间系统是将输入序列变换成输出序列的一种运算。

离散时间系统中最重要、最常用的是“线性时不变系统”。

1.线性系统满足叠加原理的系统称为线性系统，即若某一输入是由N个信号的加权和组成的，则输出就是系统对这几个信号中每一个输入的响应的加权和。

即那么当且仅当系统同时满足和时，系统是线性的。

在证明一个系统是线性系统时，必须证明此系统同时满足可加性和比例性，而且信号以及任何比例系数都可以是复数。

2.时不变系统系统的运算关系在整个运算过程中不随时间（也即序列的先后）而变化，这种系统称为时不变系统（或称移不变系统）。

若输入的输出为，则将输入序列移动任意位后，其输出序列除了跟着位移外，数值应该保持不变，即则满足以上关系的系统称为时不变系统。

3.常系数线性差分方程线性时不变离散系统的输入、输出关系可用以下常系数线性差分方程描述：当输入为单位冲激序列时，输出即为系统的单位冲激响应。

当时，是有限长度的，称系统为有限长单位冲激响应（FIR）系统；反之，则称系统为无限长单位冲激响应（IIR）系统。

三．实验内容及实验结果1.实验内容考虑如下差分方程描述的两个离散时间系统：系统1：系统2：输入：（1）编程求上述两个系统的输出，并画出系统的输入与输出波形。

（2）编程求上述两个系统的冲激响应序列，并画出波形。

（3）若系统的初始状态为零，判断系统2是否为时不变的？是否为线性的？2.实验结果（1）编程求上述两个系统的输出和冲激响应序列，并画出系统的输入、输出与冲激响应波形。

clf;n=0:300;x=cos((20*pi*n)/256)+cos((200*pi*n)/256);num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=filter(num1,den1,x);y2=filter(num2,den2,x);subplot(3,1,1);stem(n,x);xlabel('时间信号');ylabel('信号幅度');title('输入信号');subplot(3,1,2);stem(y1);xlabel('时间信号n');ylabel('信号幅度');title('输出信号');subplot(3,1,3);stem(y2);xlabel('时间序号n ');ylabel('信号幅度');title('冲激响应序列');（2）N=40;num1=[0.5 0.27 0.77];den1=[1];num2=[0.45 0.5 0.45];den2=[1 -0.53 0.46];y1=impz(num1,den1,N);y2=impz(num2,den2,N);subplot(2,1,1);stem(y1);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');subplot(2,1,2);stem(y2);xlabel('时间信号n ');ylabel('信号幅度');title('³冲激响应');1.应用叠加原理验证系统2是否为线性系统：clear allclcn = 0 : 1 : 299;x1 = cos(20 * pi * n / 256);x2 = cos(200 * pi * n / 256);x = x1 + x2;num = [0.45 0.5 0.45];den = [1 -0.53 0.46];y1 = filter(num, den, x1);y2 = filter(num, den, x2);y= filter(num, den, x);yt = y1 + y2;figuresubplot(2, 1, 1);stem(n, y, 'g');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;subplot(2, 1, 2);stem(n, yt, 'r');xlabel('时间信号n');ylabel('信号幅度');axis([0 100 -2 2]);grid;2.应用时延差值来判断系统2是否为时不变系统。

第七章离散时间系统的时域分析§7-1 概述一、离散时间信号与离散时间系统离散时间信号：只在某些离散的时间点上有值的信号。

离散时间系统：处理离散时间信号的系统。

混合时间系统：既处理离散时间信号，又处理连续时间信号的系统。

二、连续信号与离散信号连续信号可以转换成离散信号，从而可以用离散时间系统（或数字信号处理系统）进行处理：三、离散信号的表示方法：1、 时间函数：f(k)<——f(kT)，其中k 为序号，相当于时间。

例如：)1.0sin()(k k f =2、 （有序）数列：将离散信号的数值按顺序排列起来。

例如：f(k)={1,0.5,0.25,0.125,……,}时间函数可以表达任意长（可能是无限长）的离散信号，可以表达单边或双边信号，但是在很多情况下难于得到；数列的方法表示比较简单，直观，但是只能表示有始、有限长度的信号。

四、典型的离散时间信号1、 单位样值函数：⎩⎨⎧==其它001)(k k δ 下图表示了)(n k −δ的波形。

这个函数与连续时间信号中的冲激函数)(t δ相似，也有着与其相似的性质。

例如：)()0()()(k f k k f δδ=，)()()()(000k k k f k k k f −=−δδ。

2、 单位阶跃函数：⎩⎨⎧≥=其它001)(k k ε这个函数与连续时间信号中的阶跃函数)(t ε相似。

用它可以产生（或表示）单边信号（这里称为单边序列）。

3、 单边指数序列：)(k a k ε比较：单边连续指数信号：)()()(t e t e t a at εε=，其底一定大于零，不会出现负数。

(a) 0.9a = (d) 0.9a =−(b) 1a = (e) 1a =−(c) 1.1a = (f) 1.1a =−4、 单边正弦序列：)()cos(0k k A εφω+双边正弦序列：)cos(0φω+k A五、离散信号的运算1、 加法：)()()(21k f k f k f +=<—相同的k 对应的数相加。

离散时间系统频域分析离散时间系统的频域分析是研究离散时间信号在频域上的性质和行为的方法。

在离散时间系统频域分析中，使用离散时间傅里叶变换（Discrete Fourier Transform，DFT），来将离散时间信号从时域转换到频域。

通过分析信号在频域上的频谱分布和频谱特性，可以得到离散时间系统的频率响应和频域特性，对信号的频域分布和频率区间进行评估和分析。

离散时间傅里叶变换是时域信号分析的重要工具，它可以将离散时间信号从时域转换到频域。

离散时间傅里叶变换的定义可以表示为：X(k) = Σ[x(n) * exp(-j*2πkn/N)]其中，X(k)是离散时间信号在频域的频谱，x(n)是离散时间信号，N是信号的长度，k是频谱的索引。

离散时间傅里叶变换将时域信号分解成多个频率成分，通过频谱的幅度和相位信息，可以得到信号在频域上的分布情况。

通过离散时间傅里叶变换可以得到离散时间信号的频谱，进而分析信号在频域上的频率响应和频域特性。

频谱可以反映信号在不同频率上的能量分布情况，通过观察频谱的幅度和相位，可以得到信号的频率成分、频带宽度和频率特性等信息。

在离散时间系统频域分析中，常用的分析工具有频谱图、功率谱密度、频率响应等。

频谱图可以将信号的频谱以图形形式展示出来，通过观察频谱图的形状和分布，可以得到信号在频域上的特点。

功率谱密度是指信号在不同频率上的功率分布情况，可以评估信号在不同频率上的能量分布情况。

频率响应是指系统对不同频率信号的响应情况，可以评估系统对不同频率信号的滤波和增益特性。

离散时间系统频域分析的应用包括信号处理、通信系统、控制系统等领域。

在信号处理中，通过频域分析可以对信号进行滤波、去噪、频域变换等操作，提高信号的质量和分析能力。

在通信系统中，通过频域分析可以评估信号传输和接收的性能，并对系统进行优化和改进。

在控制系统中，通过频域分析可以评估系统的稳定性和控制特性，提高系统的响应速度和稳定性。

离散时间系统分析离散时间系统分析是指对离散时间信号和系统的特性进行研究和分析的过程。

离散时间信号是在时间上是离散的，而连续时间信号则是在时间上是连续的。

离散时间系统是指对离散时间信号进行输入输出变换的系统。

离散时间系统分析主要包括对离散时间信号和系统的表示、性质、分析和设计等方面的内容。

离散时间信号的表示离散时间信号可以通过数学方法进行表示和描述。

常用的表示方法包括序列表示法和函数表示法。

序列表示法是离散时间信号的一种常见表示方式，它将离散时间信号看作是一个序列，表示为一个有序的数值列表。

序列可以分为有限序列和无限序列两种。

有限序列表示了在有限时间内的信号取值，而无限序列表示了在无限时间内的信号取值。

函数表示法是另一种常用的离散时间信号的表示方式，它使用数学函数来描述信号的取值。

函数表示法更加灵活，可以表示各种复杂的离散时间信号，如周期序列、随机信号等。

离散时间系统的性质离散时间系统可以根据其性质进行分类和分析。

其中包括线性性、时不变性、因果性和稳定性等。

线性性是指系统的输出与输入之间存在线性关系。

如果系统满足输入信号的线性性质，那么对于任意输入信号x1(n)和x2(n)，以及对应的输出信号y1(n)和y2(n)，系统将满足以下性质：•线性叠加性：对于任意的实数a和b，有系统对于输入信号ax1(n)+bx2(n)的输出为ay1(n)+by2(n)。

时不变性是指系统的输出与输入之间的关系不随时间的变化而变化。

如果系统满足输入信号的时不变性质，那么对于任意输入信号x(n)和对应的输出信号y(n)，如果将输入信号延时d个单位时间，那么对应的输出信号将也会延时d个单位时间。

因果性是指系统的输出只取决于当前和过去的输入值，不受未来输入值的影响。

如果系统满足输入信号的因果性质，那么对于任意n的值，系统的输出信号y(n)只取决于输入信号x(n)及其过去的值。

稳定性是指系统的输出有界，不会无限增长。

如果系统满足输入信号的稳定性质，那么对于任意有界输入序列，输出序列也将是有界的。

实验三 离散时间系统的时域分析1.实验目的（1）理解离散时间信号的系统及其特性。

（2）对简单的离散时间系统进行分析，研究其时域特性。

（3）利用MATLAB 对离散时间系统进行仿真，观察结果，理解其时域特性。

2.实验原理离散时间系统，主要是用于处理离散时间信号的系统，即是将输入信号映射成的输出的某种运算，系统的框图如图所示：][n x ][n y Discrete-timesystme（1）线性系统线性系统就是满足叠加原理的系统。

如果对于一个离散系统输入信号为12(),()x n x n 时，输出信号分别为12(),()y n y n ，即：1122()[()]()[()]y n T x n y n T x n ==。

而且当该系统的输入信号为12()()ax n bx n +时，其中a,b 为任意常数，输出为121212[()()][()][()]()()T ax n bx n aT x n bT x n ay n by n +=+=+，则该系统就是一个线性离散时间系统。

（2）时不变系统如果系统的响应与激励加于系统的时刻无关，则该系统是时不变系统。

对于一个离散时间系统，若输入()x n ，产生输出为()y n ，则输入为()x n k -，产生输出为()y n k -，即：若()[()]y n T x n =，则[()]()T x n k y n k -=-。

通常我们研究的是线性时不变离散系统。

3.实验内容及其步骤（1）复习离散时间系统的主要性质，掌握其原理和意义。

（2）一个简单的非线性离散时间系统的仿真 参考：% Generate a sinusoidal input signalclf; n = 0:200; x = cos(2*pi*0.05*n); % Compute the output signal x1 = [x 0 0]; % x1[n] = x[n+1] x2 = [0 x 0]; % x2[n] = x[n] x3 = [0 0 x];% x3[n] = x[n-1]y = x2.*x2-x1.*x3; y = y(2:202); % Plot the input and output signalssubplot(2,1,1) plot(n, x)xlabel('Time index n'); ylabel('Amplitude'); title('Input Signal')subplot(2,1,2) plot(n,y)xlabel('Time index n'); ylabel('Amplitude');title('Output signal');（3）线性与非线性系统的仿真参考：% Generate the input sequencesclf; n = 0:40; a = 2; b = -3;x1 = cos(2*pi*0.1*n); x2 = cos(2*pi*0.4*n);x = a*x1 + b*x2;num = [2.2403 2.4908 2.2403];den = [1 -0.4 0.75];ic = [0 0]; % Set zero initial conditionsy1 = filter(num,den,x1,ic); % Compute the output y1[n]y2 = filter(num,den,x2,ic); % Compute the output y2[n]y = filter(num,den,x,ic); % Compute the output y[n]yt = a*y1 + b*y2; d = y - yt; % Compute the difference output d[n] % Plot the outputs and the difference signalsubplot(3,1,1) stem(n,y); ylabel('Amplitude');title('Output Due to Weighted Input: a \cdot x_{1}[n] + b \cdot x_{2}[n]');subplot(3,1,2) stem(n,yt); ylabel('Amplitude');title('Weighted Output: a \cdot y_{1}[n] + b \cdot y_{2}[n]');subplot(3,1,3) stem(n,d); xlabel('Time index n'); ylabel('Amplitude');title('Difference Signal');（4）时不变与时变系统的仿真参考：% Generate the input sequencesclf; n = 0:40; D = 10; a = 3.0; b = -2;x = a*cos(2*pi*0.1*n) + b*cos(2*pi*0.4*n);xd = [zeros(1,D) x]; num = [2.2403 2.4908 2.2403]; den = [1 -0.4 0.75];ic = [0 0]; % Set initial conditions% Compute the output y[n]y = filter(num,den,x,ic);% Compute the output yd[n]yd = filter(num,den,xd,ic);% Compute the difference output d[n]d = y - yd(1+D:41+D);% Plot the outputssubplot(3,1,1) stem(n,y); ylabel('Amplitude'); title('Output y[n]'); grid;subplot(3,1,2) stem(n,yd(1:41)); ylabel('Amplitude');title(['Output due to Delayed Input x[n - ', num2str(D),']']); grid;subplot(3,1,3) stem(n,d); xlabel('Time index n'); ylabel('Amplitude');title('Difference Signal'); grid;4.实验用MATLAB函数介绍在实验过程中，MATLAB函数命令plot, figure, stem, subplot, axis, grid on, xlabel, ylabel, title, clc等在不同的情况下具体表述也有所不同，应该在实验中仔细体会其不同的含义。

离散时间系统的时域分析离散时间系统是指系统输入和输出信号都是在离散的时间点上进行采样的系统。

时域分析是分析系统在时域上的性质和特征。

在离散时间系统的时域分析中，常用的方法包括冲击响应法、单位样值法和差分方程法等。

冲击响应法是通过对系统施加单个冲击信号，观察系统在输出上的响应来分析系统的时域特征。

冲击响应法的基本思想是将系统的输出表示为输入信号与系统的冲击响应之间的卷积运算。

冲击响应法适用于线性时不变系统，在实际应用中可以使用软件工具进行计算。

单位样值法是通过将系统输入信号取为单位样值序列，观察系统在输出上的响应来分析系统的时域特征。

单位样值法的基本思想是将系统的输出表示为输入信号与系统的单位样值响应之间的卷积运算。

单位样值法适用于线性时不变系统，可以用来计算系统的单位样值响应和单位样值响应序列。

差分方程法是通过建立系统输入和输出之间的差分方程来分析系统的时域特征。

差分方程法的基本思想是根据系统的差分方程，利用系统的初始条件和输入序列，递推计算系统的输出序列。

差分方程法适用于线性时不变系统，可以用来计算系统的单位样值响应和任意输入信号下的输出序列。

以上所述的方法是离散时间系统时域分析中常用的方法，通过这些方法可以获得系统的冲击响应、单位样值响应和任意输入信号下的输出序列，进而分析系统的时域特征和性质。

在实际应用中，根据系统的具体情况和需求，选择合适的方法进行时域分析，能够更好地理解离散时间系统的动态行为和响应特性。

离散时间系统的时域分析是研究系统在离散时间上的动态行为和响应特性的关键方法。

通过分析系统的时域特征，可以深入了解系统的稳定性、响应速度、频率选择性和滤波特性等方面的性能。

冲击响应法是离散时间系统常用的时域分析方法之一。

它通过施加一个单个的冲击信号，即输入信号序列中只有一个非零元素，然后观察系统在输出上的响应。

这样可以得到系统的冲击响应序列，它描述了系统对单位幕函数输入信号的响应情况。

冲击响应法的核心思想是将系统的输出表示为输入信号序列与系统的冲击响应序列之间的卷积运算。