下载文档原格式
线性微分⽅程简介
Δy表⽰的是变量y的变化量。
微分（differential），即微变化量，数学上表⽰为dy，dy被成为different of y。
导数（derivative），即变化率，数学上表⽰为dy
dt，也就是极短时间内y的变化量。
线性微分⽅程（Linear differential equations）有如下⽅式表⽰
Ly=f
其中L为线性操作符，y为需要求的未知函数，f是⼀个与y具有相同⾃变量的函数，即可写成下⾯的形式
L[y(t)]=f(t)
既然是线性微分⽅程，那么左侧的线性操作符内仅含有⼀次（1st-degree）项（线性，即不含有y2,(y′)5等的多次项），并且各项会有未知函数y的导数，那么等式左侧展开得到
L[y(t)]=d n y
d n t+A
1
d n−1t
d n−1t+⋅⋅⋅+A
n−1
dy
dt+A
n y
其中A k,k=1,2,…,n为该多项式的系数。
最⾼阶导数为d n y
d n t（nth-order）。
由于⼤部分函数都能展开成形式，因此线性微分⽅程的⼀般求解⽅法是假设所求的未知函数y为幂级数，以此来求解：
y=
∞
∑
k=0a k t k
把左边的y相关项替换成幂级数形式，最终左右两边相同次⽅的项的系数应该相等，以此来求得y。
Processing math: 100%。
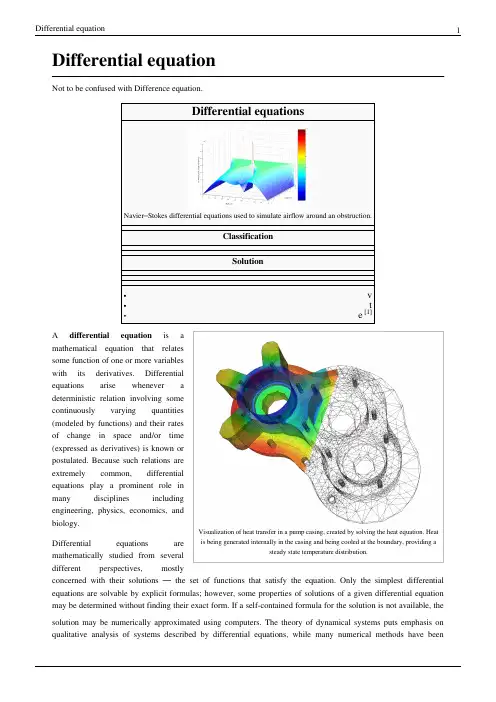
Differential equationNot to be confused with Difference equation.Stokes differential equations used to simulate airflow around an obstruction.ClassificationSolutionVisualization of heat transfer in a pump casing, created by solving the heat equation. Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution.A differential equation is amathematical equation that relatessome function of one or more variableswith its derivatives. Differentialequations arise whenever adeterministic relation involving somecontinuously varying quantities(modeled by functions) and their ratesof change in space and/or time(expressed as derivatives) is known orpostulated. Because such relations areextremely common, differentialequations play a prominent role inmany disciplines includingengineering, physics, economics, andbiology.Differential equations aremathematically studied from severaldifferent perspectives, mostlyconcerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form. If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have beendeveloped to determine solutions with a given degree of accuracy.ExampleFor example, in classical mechanics, the motion of a body is described by its position and velocity as the time value varies. Newton's laws allow one (given the position, velocity, acceleration and various forces acting on the body) to express these variables dynamically as a differential equation for the unknown position of the body as a function of time.In some cases, this differential equation (called an equation of motion) may be solved explicitly.An example of modelling a real world problem using differential equations is the determination of the velocity of a ball falling through the air, considering only gravity and air resistance. The ball's acceleration towards the ground is the acceleration due to gravity minus the acceleration due to air resistance. Gravity is considered constant, and air resistance may be modeled as proportional to the ball's velocity. This means that the ball's acceleration, which is a derivative of its velocity, depends on the velocity (and the velocity depends on time). Finding the velocity as a function of time involves solving a differential equation and verifying its validity.Directions of studyThe study of differential equations is a wide field in pure and applied mathematics, physics, and engineering. All of these disciplines are concerned with the properties of differential equations of various types. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of the methods for approximating solutions. Differential equations play an important role in modelling virtually every physical, technical, or biological process, from celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems may not necessarily be directly solvable, i.e. do not have closed form solutions. Instead, solutions can be approximated using numerical methods.Mathematicians also study weak solutions (relying on weak derivatives), which are types of solutions that do not have to be differentiable everywhere. This extension is often necessary for solutions to exist.The study of the stability of solutions of differential equations is known as stability theory.NomenclatureThe theory of differential equations is well developed and the methods used to study them vary significantly with the type of the equation.Ordinary and partial•An ordinary differential equation (ODE) is a differential equation in which the unknown function (also known as the dependent variable) is a function of a single independent variable. In the simplest form, the unknown function is a real or complex valued function, but more generally, it may be vector-valued or matrix-valued: this corresponds to considering a system of ordinary differential equations for a single function.Ordinary differential equations are further classified according to the order of the highest derivative of the dependent variable with respect to the independent variable appearing in the equation. The most important cases for applications are first-order and second-order differential equations. For example, Bessel's differential equation(in which y is the dependent variable) is a second-order differential equation. In the classical literature a distinction is also made between differential equations explicitly solved with respect to the highest derivative and differential equations in an implicit form. Also important is the degree, or (highest) power, of the highest derivative(s) in the equation (cf. : degree of a polynomial). A differential equation is called a nonlinear differential equation if its degree is not one (a sufficient but unnecessary condition).• A partial differential equation (PDE) is a differential equation in which the unknown function is a function of multiple independent variables and the equation involves its partial derivatives. The order is defined similarly to the case of ordinary differential equations, but further classification into elliptic, hyperbolic, and parabolic equations, especially for second-order linear equations, is of utmost importance. Some partial differentialequations do not fall into any of these categories over the whole domain of the independent variables and they are said to be of mixed type.Linear and non-linearBoth ordinary and partial differential equations are broadly classified as linear and nonlinear.• A differential equation is linear if the unknown function and its derivatives appear to the power 1 (products of the unknown function and its derivatives are not allowed) and nonlinear otherwise. The characteristic property of linear equations is that their solutions form an affine subspace of an appropriate function space, which results in much more developed theory of linear differential equations. Homogeneous linear differential equations are a further subclass for which the space of solutions is a linear subspace i.e. the sum of any set of solutions or multiples of solutions is also a solution. The coefficients of the unknown function and its derivatives in a linear differential equation are allowed to be (known) functions of the independent variable or variables; if these coefficients are constants then one speaks of a constant coefficient linear differential equation.•There are very few methods of solving nonlinear differential equations exactly; those that are known typically depend on the equation having particular symmetries. Nonlinear differential equations can exhibit verycomplicated behavior over extended time intervals, characteristic of chaos. Even the fundamental questions of existence, uniqueness, and extendability of solutions for nonlinear differential equations, and well-posedness of initial and boundary value problems for nonlinear PDEs are hard problems and their resolution in special cases is considered to be a significant advance in the mathematical theory (cf. Navier–Stokes existence and smoothness).However, if the differential equation is a correctly formulated representation of a meaningful physical process, then one expects it to have a solution.Linear differential equations frequently appear as approximations to nonlinear equations. These approximations are only valid under restricted conditions. For example, the harmonic oscillator equation is an approximation to the nonlinear pendulum equation that is valid for small amplitude oscillations (see below).ExamplesIn the first group of examples, let u be an unknown function of x, and c and ω are known constants.•Inhomogeneous first-order linear constant coefficient ordinary differential equation:•Homogeneous second-order linear ordinary differential equation:•Homogeneous second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:•Inhomogeneous first-order nonlinear ordinary differential equation:•Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:In the next group of examples, the unknown function u depends on two variables x and t or x and y.•Homogeneous first-order linear partial differential equation:•Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:•Third-order nonlinear partial differential equation, the Korteweg–de Vries equation:Related concepts• A delay differential equation (DDE) is an equation for a function of a single variable, usually called time, in which the derivative of the function at a certain time is given in terms of the values of the function at earlier times.• A stochastic differential equation (SDE) is an equation in which the unknown quantity is a stochastic process and the equation involves some known stochastic processes, for example, the Wiener process in the case of diffusion equations.• A differential algebraic equation (DAE) is a differential equation comprising differential and algebraic terms, given in implicit form.Connection to difference equationsSee also: Time scale calculusThe theory of differential equations is closely related to the theory of difference equations, in which the coordinates assume only discrete values, and the relationship involves values of the unknown function or functions and values at nearby coordinates. Many methods to compute numerical solutions of differential equations or study the properties of differential equations involve approximation of the solution of a differential equation by the solution of a corresponding difference equation.Universality of mathematical descriptionMany fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics, differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed together with the sciences where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second-order partial differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat, the theory of which was developed by Joseph Fourier, is governed by another second-order partial differential equation, the heat equation. It turns out that many diffusion processes, while seemingly different, are described by the same equation; the Black–Scholes equation in finance is, for instance, related to the heat equation.Notable differential equationsPhysics and engineering•Newton's Second Law in dynamics (mechanics)•Euler–Lagrange equation in classical mechanics•Hamilton's equations in classical mechanics•Radioactive decay in nuclear physics•Newton's law of cooling in thermodynamics•The wave equation•Maxwell's equations in electromagnetism•The heat equation in thermodynamics•Laplace's equation, which defines harmonic functions•Poisson's equation•Einstein's field equation in general relativity•The Schrödinger equation in quantum mechanics•The geodesic equation•The Navier–Stokes equations in fluid dynamics•The Diffusion equation in stochastic processes•The Convection–diffusion equation in fluid dynamics•The Cauchy–Riemann equations in complex analysis•The Poisson–Boltzmann equation in molecular dynamics•The shallow water equations•Universal differential equation•The Lorenz equations whose solutions exhibit chaotic flow.Biology•Verhulst equation – biological population growth•von Bertalanffy model – biological individual growth•Lotka–Volterra equations – biological population dynamics•Replicator dynamics – found in theoretical biology•Hodgkin–Huxley model – neural action potentialsEconomics•The Black–Scholes PDE•Exogenous growth model•Malthusian growth model•The Vidale–Wolfe advertising modelReferences•P. Abbott and H. Neill, Teach Yourself Calculus, 2003 pages 266-277•P. Blanchard, R. L. Devaney, G. R. Hall, Differential Equations, Thompson, 2006• E. A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955• E. L. Ince, Ordinary Differential Equations, Dover Publications, 1956•W. Johnson, A Treatise on Ordinary and Partial Differential Equations[2], John Wiley and Sons, 1913, in University of Michigan Historical Math Collection [3]• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.•R. I. Porter, Further Elementary Analysis, 1978, chapter XIX Differential Equations•Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems[4]. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.[1]/w/index.php?title=Template:Differential_equations&action=edit[2]/cgi/b/bib/bibperm?q1=abv5010.0001.001[3]/u/umhistmath/[4]http://www.mat.univie.ac.at/~gerald/ftp/book-ode/External links•Lectures on Differential Equations (/courses/mathematics/18-03-differential-equations-spring-2010/video-lectures/) MIT Open CourseWare Videos•Online Notes / Differential Equations (/classes/de/de.aspx) Paul Dawkins, Lamar University•Differential Equations (/diffeq/diffeq.html), S.O.S. Mathematics•Differential Equation Solver (/tools/differential_equation_solver/) Java applet tool used to solve differential equations.•Introduction to modeling via differential equations (/mat/u-u/en/ differential_equations_intro.htm) Introduction to modeling by means of differential equations, with critical remarks.•Mathematical Assistant on Web (http://user.mendelu.cz/marik/maw/index.php?lang=en&form=ode) Symbolic ODE tool, using Maxima•Exact Solutions of Ordinary Differential Equations (http://eqworld.ipmnet.ru/en/solutions/ode.htm)•Collection of ODE and DAE models of physical systems (/research/models.htm) MATLAB models•Notes on Diffy Qs: Differential Equations for Engineers (/diffyqs/) An introductory textbook on differential equations by Jiri Lebl of UIUC•Khan Academy Video playlist on differential equations (/math/ differential-equations) Topics covered in a first year course in differential equations.•MathDiscuss Video playlist on differential equations (/category/courses/ solutions-differential-equations/homogeneous-linear-systems/)Article Sources and Contributors8Article Sources and ContributorsDifferential equation Source: /w/index.php?oldid=610771276 Contributors: 17Drew, After Midnight, Ahoerstemeier, Alarius, Alfred Centauri, Amahoney, AndreiPolyanin, Andres, AndrewHowse, Andycjp, Andytalk, AngryPhillip, Anonymous Dissident, Antoni Barau, Antonius Block, Anupam, Apmonitor, Arcfrk, Asdf39, Asyndeton, Attilios,Babayagagypsies, Baccala@, Baccyak4H, Bejohns6, Bento00, Berland, Bidabadi, Bigusbry, BillyPreset, Bob.v.R, Bolatbek, Brandon, Bryanmcdonald, Btyner, Bygeorge2512,Callumds, Charles Matthews, Christian75, Chtito, Cispyre, Cmprince, Coginsys, ConMan, Cxz111, Cybercobra, DAJF, Danski14, Dbroadwell, Ddxc, Delaszk, DerHexer, Dewritech, Difu Wu, Djordjes, DominiqueNC, Donludwig, Dpv, Dr sarah madden, Drmies, DroEsperanto, Duoduoduo, Dysprosia, EconoPhysicist, Elwikipedista, Epicgenius, EricBright, Erin.Annette.Brown,Estudiarme, F=q(E+v^B), Fintor, Fioravante Patrone, Fioravante Patrone en, Flameturtle, Friend of the Facts, FutureTrillionaire, Gabrielleitao, Gandalf61, Gauss, Genedronek, Geni, Giftlite,GoingBatty, Gombang, Grenavitar, Haham hanuka, Hamiltondaniel, Harry, Haruth, Haseeb Jamal, Heikki m, Holmes1900, Ilya Voyager, Iquseruniv, Iulianu, Izodman2012, J arino, J.delanoy, Ja 62, Jak86, JamesBWatson, Jao, Jarble, Jauhienij, Jayden54, Jeancey, Jersey Devil, Jim Sukwutput, Jim.belk, Jim.henderson, JinJian, Jitse Niesen, JohnOwens, Johndoeisnotmyname, JorisvS,Julesd, K-UNIT, Kayvan45622, KeithJonsn, Kensaii, Khalid Mahmood, Klaas van Aarsen, Kr5t, Krushia, LOL, Lambiam, Lavateraguy, Lethe, LibLord, Linas, Lumos3, Madmath789, Mandarax, Mankarse, MarSch, Martastic, Martynas Patasius, Maschen, Math.geek3.1415926, Matqkks, Mattmnelson, Maurice Carbonaro, Maxis ftw, Mazi, McVities, Mduench, Mets501, Mh, MichaelHardy, Mindspillage, MisterSheik, Mohan1986, Mossaiby, Mpatel, MrOllie, Mtness, Mysidia, Nik-renshaw, Nkayesmith, Norm mit, Okopecz, Oleg Alexandrov, Opelio, Pahio, Parusaro, Paul August, Paul Matthews, Paul Richter, PavelSolin, Pgk, Phoebe, Pine, Pinethicket, Pratyya Ghosh, PseudoSudo, Qwerty Binary, Qzd800, R'n'B, Rama's Arrow, Randomguess, Reallybored999, RexNL, Reyk, RichMorin, Robin S, Romansanders, Rosasco, Ruakh, SDC, SFC9394, SakeUPenn, Salix alba, Sam Staton, Sampathsris, Sardanaphalus, Senoreuchrestud, Silly rabbit, Siroxo,Skakkle, Skypher, SmartPatrol, Snowjeep, Spirits in the Material, Starwiz, Suffusion of Yellow, Sverdrup, Symane, TVBZ28, TYelliot, Tannkrem, Tbhotch, Tbsmith, TexasAndroid, Tgeairn, The Hybrid, The Thing That Should Not Be, Timelesseyes, Tranum1234567890, Tsirel, Tuseroni, User A1, Vanished User 0001, Vishwanathnm, Vthiru, Waffleguy4, Waldir, Waltpohl, Wavelength, Wclxlus, Wihenao, Willtron, Winterheart, Wsears, XJaM, Yafujifide, Zepterfd, ﺪﺟﺎﺳ ﺪﺠﻣﺍ ﺪﺟﺎﺳ, 363 anonymous editsImage Sources, Licenses and ContributorsFile:Airflow-Obstructed-Duct.png Source: /w/index.php?title=File:Airflow-Obstructed-Duct.png License: Public Domain Contributors: Original uploader was User A1 at en.wikipediaFile:Elmer-pump-heatequation.png Source: /w/index.php?title=File:Elmer-pump-heatequation.png License: Creative Commons Attribution-Sharealike 3.0Contributors: Christian1985, Crimerob, Kri, User A1, 2 anonymous editsLicenseCreative Commons Attribution-Share Alike 3.0///licenses/by-sa/3.0/。
数学的微分方程与动力学微分方程（Differential Equations）是数学分析的重要分支，研究的是函数与其导数或微分之间的关系。
微分方程在许多科学领域，尤其是在动力学（Dynamics）中扮演着重要的角色。
本文将探讨数学的微分方程与动力学的关系，揭示它们之间的密切联系。
一、微分方程的基础微分方程是描述物理、生物、经济等现象的最常用工具之一。
数学上，它可以分为常微分方程和偏微分方程两类。
常微分方程涉及一个或多个未知函数及其自变量的导数，而偏微分方程则涉及了多个自变量的导数。
微分方程提供了一种描述变化过程的数学语言，解它们可以揭示出物理系统的演化规律。
二、动力学的基本概念动力学关注系统随时间演化的规律，研究物体的运动以及与运动有关的力和能量的转化。
它是自然科学中的一个重要分支，涉及力学、物理学、生物学等多个领域。
动力学看似与微分方程没有直接联系，但实际上微分方程是研究动力学的主要工具之一。
三、微分方程与动力学的联系微分方程与动力学有着紧密的联系。
动力学问题通常可以通过建立微分方程来描述。
以经典力学为例，牛顿第二定律F=ma可以通过将加速度a与速度v和位移x的关系表示为v'=a、x'=v，构建出微分方程。
这个微分方程可以求解，得出物体的位置随时间的变化规律。
四、微分方程在动力学中的应用微分方程在动力学中被广泛应用。
在经济学中，微分方程可以用来描述市场供需关系的变化；在生物学中，微分方程可以用来描述生物种群的增长和衰减规律；在物理学中，微分方程可以用来描述电路中电流和电压的变化。
五、数值解法与动力学仿真微分方程通常难以直接求解，因此数值解法和动力学仿真成为解决微分方程问题的重要手段。
数值解法通过将微分方程转化为差分方程，离散化求解得到近似解；而动力学仿真则通过模拟系统的演化过程，得到系统的行为和发展趋势。
六、微分方程与混沌理论混沌理论是动力学的一个重要分支，研究的是非线性系统中表现出的复杂行为。
Chapter 1 First-order ordinary differential equations (ODE)一階常微分方程1.1 基本概念()x f y =或()t f y =，y 是x 或t 的函數，y 是因變數(dependent variable )，x 或t 是自變數(independent variable )◎ 微分方程(differential equations)：一方程式包含有因變數y 關於自變數x 或t的導數(derivatives)y y ′ ,&或微分(differentials)dy 。
◎ 常微分方程(ordinary differential equations, ODE)：一微分方程包含有一個或數個因變數（通常為()x y ）關於僅有一個自變數x 的導數。
Ex. 222)2(2 ,09 ,cos y x y e y y x y y x y x +=′′+′′′′=+′′=′◎ 偏微分方程(partial differential equations, PDE)：一微分方程包含至少有一個因變數關於兩個以上自變數的部分導數。
Ex. 02222=∂∂+∂∂yux u◎ 微分方程的階數：在微分方程式中所出現最高階導數的階數。
◎ 線性微分方程：在微分方程式中所出現的因變數因變數因變數或其導數僅有一次式(first degree)而無二次以上的乘積（自變數可以有二次以上的乘積）。
Ex. x y y x y cos 24=+′+′′ 因變數：y ，自變數：x ，二階線性常微分方程 x y y y y cos 24=+′+′′ 因變數：y ，自變數：x ，二階非線性常微分方程 222)2(2 y x y e y y x x +=′′+′′′′ 因變數：y ，自變數：x ，三階非線性常微分方程□ 一階常微分方程(first-order ordinary differential equations)隱式形式(implicit form) 表示 0),,(=′y y x F (4)顯式形式(explicit form) 表示 ),(y x f y =′Ex. 隱式形式ODE 0423=−′−y y x ，當0≠x 時，可表示為顯式形式234y x y =′□ 解的概念(concept of solution)在某些開放間隔區間b x a <<，一函數)(x h y =是常微分方程常微分方程0),,(=′y y x F 的解，其函數)(x h 在此區間b x a <<是明確(defined)且可微分的(differentiable)，其)(x h 的曲線（或圖形）是被稱為解答曲線(solution curve)。
Further math（高等数学）是数学领域的一个重要分支，它深入探讨和研究了一些基本数学概念和定理，为未来的研究和应用奠定了坚实的基础。
在这篇文章中，我将以“step by step thinking”的方式来介绍一些Further math的知识点，帮助读者更好地理解和应用这些概念。
1.极限（Limits）：极限是Further math中的一个重要概念，它描述了函数在某一点附近的行为。
通过逐渐靠近某个点的过程，我们可以了解函数在该点的趋势和性质。
极限的计算和理解是解决各种数学问题的基础。
2.微分（Differentiation）：微分是Further math中的另一个核心概念，它研究函数的变化率和斜率。
通过微分，我们可以求解函数的极值点、优化问题，并揭示函数图像的特征。
微分在物理学、经济学等领域有着广泛的应用。
3.积分（Integration）：积分是微分的逆运算，它求解函数的面积、体积等量。
通过积分，我们可以解决曲线下面积、累积和总量问题。
积分在统计学、物理学等领域有着重要的应用。
4.线性代数（Linear Algebra）：线性代数是Further math中的一门重要学科，它研究向量、矩阵和线性变换等概念。
线性代数广泛应用于几何、电子工程、计算机科学等领域，并且对于理解和解决大规模线性方程组、最小二乘法等问题起着关键作用。
5.微分方程（Differential Equations）：微分方程是Further math中的一个重要分支，它研究函数及其导数之间的关系。
微分方程在物理学、工程学、生物学等领域有着广泛的应用，用于描述和预测自然界中的各种现象和过程。
6.概率论（Probability Theory）：概率论是Further math中的一门重要学科，它研究随机事件的概率和统计规律。
概率论广泛应用于金融、统计学、风险管理等领域，帮助人们做出合理的决策和预测。
在学习Further math的过程中，我们要注重“step by step”的思维方式。
数学的数值微分方程数值微分方程（Numerical Differential Equations）是数学中一个重要的研究领域，它探讨的是通过数值方法求解微分方程的问题。
微分方程是数学模型中常见的一种描述自然现象和工程问题的方程形式，而数值方法则是将微分方程转化为离散的计算问题，并通过计算机进行求解。
数值微分方程的研究由来已久，早在17世纪，数学家Newton、Euler等人就提出了一些基本的数值方法。
随着计算机的发展和数值计算技术的进步，数值微分方程的求解方法也得到了极大的发展和应用。
目前，数值微分方程的应用领域非常广泛，包括物理学、工程学、生物学、经济学等等。
数值微分方程求解的基本思想是将微分方程离散化，即将连续函数转化为离散的数值数据。
为了实现这一转化，需要将时间和空间分割成若干个小区间，在每个小区间内求解微分方程的近似解。
为了提高求解的精度，需要选择合适的离散方法，常用的方法包括有限差分法、有限元法、辛方法等。
有限差分法是数值微分方程求解中最常用的方法之一。
它的基本思想是将微分方程中的导数项用差商来近似表示，通过求解差分方程来获得微分方程的数值解。
有限差分法简单易行，计算效率高，在许多情况下能够提供较好的数值解。
有限元法是一种比较通用的数值方法，它适用于各种不规则的几何形状和复杂的边界条件。
有限元法的基本思想是将求解区域分解为有限个几何单元，通过对每个单元的逼近来得到整个区域的逼近解。
有限元法具有较高的逼近精度和灵活性，适用于一些复杂的物理问题。
辛方法是一种用于保持哈密顿系统能量守恒的数值方法，它在模拟长时间演化的系统中表现出了出色的稳定性和长期保持能量守恒的特点。
辛方法广泛应用于天体力学、分子动力学等领域的模拟计算中。
除了以上提到的方法，还有一些其他的数值方法，如龙格-库塔法、多步法、多项式插值法等，它们在不同的问题和应用中具有各自的优势和适用范围。
总之，数值微分方程是数学中重要的研究内容，通过数值方法求解微分方程可以有效地获得问题的数值解。
微分方程解法总结微分方程（DifferentialEquations）是数学中一类重要的运筹学问题，也是许多应用数学领域中最重要的数学工具之一。
微分方程可以应用在物理学、化学、工程学、生物学及经济学等学科中，在多学科领域中都发挥了重要作用。
一般来说，微分方程可以用一组方程来描述某种函数的变化，其中包括两个或更多的未知函数。
常用的微分方程解法包括，比如直接法、可积性法、积分变换法等。
1.接法直接法是指从微分方程的定义出发，直接寻找微分方程的解的方法。
一般来说，将定义域上的某个变量作为一个变量来代替原方程中的其它变量，从而将原方程变为一个关于这个变量的微分方程，再解此新的微分方程，最终得到需要的解。
2.积性法可积性法，即牛顿-拉夫逊定理，是指依据微分方程中的微分操作，运用积分学手段求出微分方程的解的方法。
牛顿-拉夫逊定理具有很强的通用性，几乎可以用于解决所有的不定积分问题，而且可以在多个变量之间进行推导。
3.分变换法积分变换法是一种特殊的可积性法，通过运用微积分中的奇偶变换，由傅里叶变换求出微分方程的解。
这种方法主要用于解决有限区间上的微分方程，既可以解决常规的微分方程，也可以解决非线性微分方程。
4.值方法数值方法是指用计算机从解析计算的角度进行微分方程的解法。
数值方法可分为两类，一类是有限差分的方法，另一类是可积性方法。
有限差分方法是在有限域上利用数值误差求解微分方程，它主要用于解决常微分方程组和椭圆型方程；可积性方法是指基于可积性定理，将微分方程转变为积分形式，再采用计算机数值解法，求出积分方程的解的方法。
总之，上述四类解法分别具有自己的优势和不足，因此要采取最适合的方式来解决某一类微分方程。
此外，在进行解微分方程的过程中，要进行精确的数学推导，以确保最终得到的解析解是准确可靠的。
通过上述分析，可以清楚地了解微分方程解法。
微分方程（Differential Equation）是数学中的一门重要的分支，指描述物理、化学、生物等各种自然现象或过程的数学方程。
下面是关于微分方程的英文介绍：Introduction：Microscopic physical and natural phenomena are often described mathematically by differential equations.Definition: A differential equation is a mathematical equation that relates some function with its derivatives.Types of Differential Equations: There are several types including ordinary differential equations (ODEs), partial differential equations (PDEs), linear and nonlinear differential equations, etc.Applications: Differential equations have many applications in physics, engineering, economics, biology, and other fields. Some examples include modeling the spread of disease, predicting the motion of planets, and analyzing the behavior of financial markets.Methods of Solving Differential Equations: There are various methods used to solve differential equations such as separation of variables, integrating factors, power series, Laplace transforms, numerical methods, and more.Future Developments: Research on differential equations continues to be an active area of study. Advances in computer technology and numerical methods have made it possible to simulate complex systems more accurately.微分方程是数学中一个广泛应用的领域，它涉及到多个层面和广泛的应用领域，需要了解基本概念、分类、应用和解法等方面的知识。
国外优秀数学教材系列微分方程
微分方程是数学中的一个重要分支，广泛应用于物理、工程、生物等领域。
为帮助学生深入理解微分方程的概念和应用，国外出版了一系列优秀的数学教材。
其中，比较经典的有《微分方程》(Differential Equations)，这是美国著名数学家Dennis G. Zill编写的一本教材。
该教材在全球范围内广受欢迎，已出版多个版本，内容涵盖微分方程的基本概念、解法和应用。
其特点是简单明了，注重实际应用，且具有丰富的例题和习题，有助于学生深入理解微分方程的本质和应用。
另外，还有《微分方程引论》(Introduction to Differential Equations)和《微分方程与边界值问题》(Differential Equations and Boundary Value Problems)等教材，这些教材均由国外一流的数学家编写，内容涵盖微分方程的基本理论和应用，对于深入学习微分方程领域的学生具有重要的参考价值。
总之，这些国外优秀的数学教材，不仅在内容上涵盖了微分方程的基本理论和应用，而且在解题方法和实践应用方面也提供了极具参考价值的案例。
希望有志于深入学习微分方程的同学们可以认真阅读这些优秀的教材，不断拓展自己的数学知识和应用能力。
- 1 -。
