SOM神经网络原理

som聚类算法SOM聚类算法是一种基于神经网络的无监督学习算法，也被称为自组织映射算法。

它可以用于数据挖掘、图像处理、模式识别等领域。

在SOM聚类算法中，通过对数据进行分组来发现数据的内在结构和规律性。

SOM聚类算法的原理是将输入数据映射到一个二维或三维的网格结构中，每个网格点都代表一个神经元。

在训练过程中，通过调整神经元之间的权重来使得相似的输入数据映射到相邻的神经元上。

这样，就可以将输入数据分成若干个簇。

SOM聚类算法有以下几个步骤：1. 初始化：随机生成一组初始权重向量，并定义一个学习率和邻域半径。

2. 选择输入：从输入数据集中随机选择一个向量。

3. 计算获胜节点：计算每个神经元与当前输入向量之间的距离，并找到与该向量距离最近的神经元作为获胜节点。

4. 更新权重向量：根据获胜节点与其它节点之间的距离和学习率来更新所有节点的权重向量。

5. 调整学习率和邻域半径：随着训练的进行，学习率和邻域半径会逐渐减小，以便更好地聚类。

6. 重复步骤2-5，直到满足停止条件。

SOM聚类算法有许多优点。

首先，它可以自适应地调整簇的数量和大小。

其次，它可以处理高维数据，并将其投影到低维空间中进行可视化。

此外，由于SOM算法是一个无监督学习算法，因此不需要先验知识或标签来指导聚类过程。

然而，SOM聚类算法也存在一些缺点。

例如，在处理大规模数据时，计算量会非常大。

此外，在选择初始权重向量时可能会出现问题，并且在某些情况下可能会收敛到局部最优解而不是全局最优解。

总之，SOM聚类算法是一种强大的无监督学习算法，在数据挖掘、图像处理、模式识别等领域中具有广泛的应用前景。

未来随着计算能力的提高以及更好的初始化方法和停止条件的发展，SOM聚类算法将变得更加有效和实用。

som管的工作原理英文回答：SOM (Self-Organizing Map) is a type of artificial neural network (ANN) that is widely used for clustering and visualization of high-dimensional data. It was first introduced by Teuvo Kohonen in the 1980s. The basic principle behind SOM is to map the input data onto a lower-dimensional grid of neurons, where each neuron represents a specific feature or pattern in the data.The working principle of SOM can be summarized in the following steps:1. Initialization: The grid of neurons is initialized with random values. Each neuron is associated with a weight vector of the same dimensionality as the input data.2. Training: The training process consists of two main phases competition and cooperation. In the competitionphase, the input data is presented to the network, and each neuron calculates its similarity to the input using a distance metric, such as Euclidean distance. The neuron with the closest weight vector to the input is declared as the winner or the Best Matching Unit (BMU).3. Adaptation: In the cooperation phase, the winning neuron and its neighboring neurons are updated to become more similar to the input data. This is done by adjusting their weight vectors based on a learning rate and a neighborhood function. The learning rate determines the amount of adjustment, while the neighborhood function defines the extent of influence from the winning neuron to its neighbors.4. Iteration: Steps 2 and 3 are repeated for a certain number of iterations or until convergence is achieved. As the training progresses, the neurons in the grid become organized in a way that preserves the topological relationships of the input data. Similar inputs tend to activate neighboring neurons, leading to the formation of clusters on the grid.5. Visualization and Analysis: Once the training is complete, the SOM can be visualized by assigning colors or labels to the neurons based on their weight vectors. This allows for the interpretation and analysis of the data in a lower-dimensional space. Additionally, the SOM can be used for tasks such as data classification, anomaly detection, and data compression.中文回答：SOM（自组织映射）是一种广泛用于高维数据聚类和可视化的人工神经网络（ANN）。

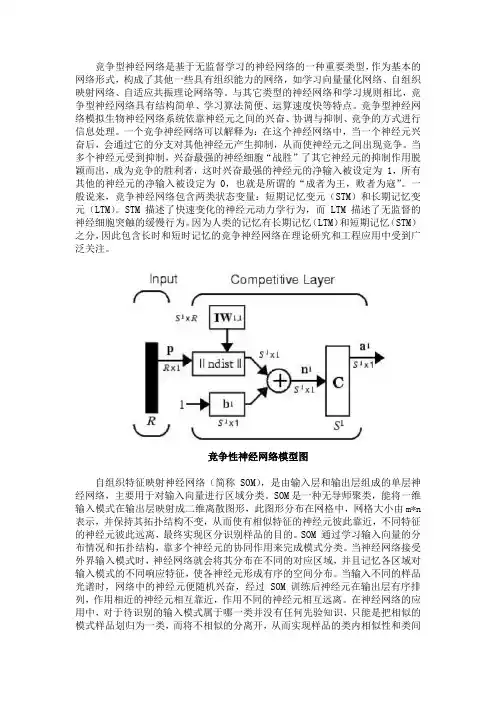
竞争型神经网络是基于无监督学习的神经网络的一种重要类型，作为基本的网络形式，构成了其他一些具有组织能力的网络，如学习向量量化网络、自组织映射网络、自适应共振理论网络等。

与其它类型的神经网络和学习规则相比，竞争型神经网络具有结构简单、学习算法简便、运算速度快等特点。

竞争型神经网络模拟生物神经网络系统依靠神经元之间的兴奋、协调与抑制、竞争的方式进行信息处理。

一个竞争神经网络可以解释为：在这个神经网络中，当一个神经元兴奋后，会通过它的分支对其他神经元产生抑制，从而使神经元之间出现竞争。

当多个神经元受到抑制，兴奋最强的神经细胞“战胜”了其它神经元的抑制作用脱颖而出，成为竞争的胜利者，这时兴奋最强的神经元的净输入被设定为 1，所有其他的神经元的净输入被设定为 0，也就是所谓的“成者为王，败者为寇”。

一般说来，竞争神经网络包含两类状态变量：短期记忆变元（STM）和长期记忆变元（LTM）。

STM 描述了快速变化的神经元动力学行为，而 LTM 描述了无监督的神经细胞突触的缓慢行为。

因为人类的记忆有长期记忆（LTM）和短期记忆（STM）之分，因此包含长时和短时记忆的竞争神经网络在理论研究和工程应用中受到广泛关注。

竞争性神经网络模型图自组织特征映射神经网络（简称SOM），是由输入层和输出层组成的单层神经网络，主要用于对输入向量进行区域分类。

SOM是一种无导师聚类，能将一维输入模式在输出层映射成二维离散图形，此图形分布在网格中，网格大小由m*n 表示，并保持其拓扑结构不变，从而使有相似特征的神经元彼此靠近，不同特征的神经元彼此远离，最终实现区分识别样品的目的。

SOM 通过学习输入向量的分布情况和拓扑结构，靠多个神经元的协同作用来完成模式分类。

当神经网络接受外界输入模式时，神经网络就会将其分布在不同的对应区域，并且记忆各区域对输入模式的不同响应特征，使各神经元形成有序的空间分布。

当输入不同的样品光谱时，网络中的神经元便随机兴奋，经过SOM 训练后神经元在输出层有序排列，作用相近的神经元相互靠近，作用不同的神经元相互远离。

数据挖掘之神经⽹络SOM算法/*神经⽹络SOM算法思想：分为输⼊层和竞争层，输⼊层就是样本的输⼊，假如我现在有5个样本A,B,C,D,E,他们是5维向量，竞争层是10*10的⼆维平⾯，相当于100个神经元，这些神经元也是5维向量，这些神经元对输⼊向量进⾏竞争，最后只有⼀个*/#include<fstream.h>#include<iomanip.h>#include<stdio.h>#include<cstdlib.h>#include<math.h>using namespace std;#define InputLayerNum 35#define OutputLayerRow 8#define OutputLayerColumn 12#define total_iteration_Num 80#define error_limit 0.0001#define efficiency 0.9int i,j,k,l,m,n;int inputMode[26][7][5];double weight[OutputLayerRow*OutputLayerColumn][InputLayerNum];int current_iteration_num=0;double study_efficiency=efficiency;double distance[OutputLayerRow*OutputLayerColumn];int neighbor_width=OutputLayerColumn;int neighbor_height=OutputLayerRow;int row[OutputLayerRow],column[OutputLayerColumn];int flag[OutputLayerRow][OutputLayerColumn];int temp_row,temp_column;int winner_row,winner_column;double min_distance=1000.0;/****************************************************///该函数初始化距离变量为0，初始化保存⽣胜出节点的位置的变量/****************************************************/void init_distance(){for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++)distance[i*OutputLayerColumn+j]=0.0;}/****************************************************///该函数⽤于计算欧⽒距离，并找到获胜神经元/****************************************************/void eula_distance(){int ttLow,ttUp,ppLow,ppUp;ttLow=winner_column-neighbor_width/2;ttUp=winner_column+neighbor_width/2;ppLow=winner_row-neighbor_height/2;ppUp=winner_row+neighbor_height/2;if(ttLow<0) ttLow=0;if(ttUp>=OutputLayerColumn) ttUp=OutputLayerColumn-1;if(ppLow<0) ppLow=0;if(ppUp>=OutputLayerRow) ppUp=OutputLayerRow-1;for(i=ppLow;i<=ppUp;i++)for(j=ttLow;j<=ttUp;j++){if(!(flag[i][i]==100)){for(m=0;m<7;m++)for(n=0;n<5;n++)distance[i*OutputLayerColumn+j]+=pow((inputMode[l][m][n]-weight[i*OutputLayerColumn+j][m*5+n]),2);if(distance[i*OutputLayerColumn+j]<min_distance){min_distance=distance[i*OutputLayerColumn+j];temp_row=i;temp_column=j;}}}if(current_iteration_num>0){if(min_distance<=error_limit){row[temp_row]=temp_row;row[temp_column]=temp_column;flag[temp_row][temp_column]=100;}}}/****************************************************///调整权值/****************************************************/void weight_change(){int ttLow,ttUp,ppLow,ppUp;winner_row=temp_row;winner_column=temp_column;ttLow=winner_column-neighbor_width/2;ttUp=winner_column+neighbor_width/2;ppLow=winner_row-neighbor_height/2;ppUp=winner_row+neighbor_height/2;if(ttLow<0) ttLow=0;if(ttUp>=OutputLayerColumn) ttUp=OutputLayerColumn-1;if(ppLow<0) ppLow=0;if(ppUp>=OutputLayerRow) ppUp=OutputLayerRow-1;for(i=ppLow;i<=ppUp;i++)for(j=ttLow;j<=ttUp;j++){if(!(flag[i][j]==100)){for(m=0;m<7;m++)for(n=0;n<5;n++)weight[i*OutputLayerColumn+j][m*5+n]+=study_efficiency*(inputMode[l][m][n]-weight[i*OutputLayerColumn+j][m*5+n]);}}}/****************************************************///调整学习效率以及获胜节点的邻域⼤⼩/****************************************************/void paraChange(){study_efficiency=study_efficiency*(1.0-((double)current_iteration_num)/total_iteration_Num);neighbor_width=(int)(neighbor_width*(1.0-((double)current_iteration_num)/total_iteration_Num));neighbor_height=(int)(neighbor_height*(1.0-((double)current_iteration_num)/total_iteration_Num));}/****************************************************///该函数⽤于将所有输⼊模式从⽂件中读⼊，并存放在数组inputMode中//同时进⾏权值的初始化，采⽤随机赋值的⽅法/****************************************************/void initialize(){for(i=0;i<OutputLayerRow;i++) row[i]=100;for(j=0;j<OutputLayerColumn;j++) column[j]=100;for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++) flag[i][j]=0;FILE *pf=fopen("输⼊数据.txt","a+");if(pf==NULL){cout<<"Can not input file!\n";exit(0);}for(i=0;i<26;i++)for(j=0;j<7;j++)for(k=0;k<5;k++) fscanf(pf,"%d",&inputMode[i][j][k]);//⽤于测试是否能够正确读⼊输⼊模式char character[26];for(i=0;i<26;i++) character[i]=(65+i);ofstream mode("输出数据.txt",ios::out);for(i=0;i<26;i++){mode<<character[i]<<'\n'<<endl;for(j=0;j<7;j++){for(k=0;k<5;k++) mode<<inputMode[i][j][k]<<"";mode<<"\n";}mode<<"\n\n\n";}//权值随机初始化，采⽤随机赋值的⽅法for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++)for(k=0;k<InputLayerNum;k++)weight[i*OutputLayerColumn+j][k]=(double)(rand()%101)/100.0;//⽤于测试是否能够正确初始化权值ofstream quan("初始权值.txt",ios::out);for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++){quan<<"\n\n\n"<<"Node["<<i+1<<"]["<<j+1<<"]"<<"\n";for(k=0;k<InputLayerNum;k++){if(k%5==0) quan<<"\n";quan<<setprecision(6)<<setiosflags(ios::fixed)<<weight[i*OutputLayerColumn+j][k]<<"";}quan<<"\n\n\n";}}int main(){int iteration_numbers[26];int total_num=0;char character[26];void test_netWork_1();void test_netWork_2();for(l=0;l<26;l++){iteration_numbers[l]=0;character[l]=(65+l);}initialize();for(l=0;l<26;l++){winner_row=OutputLayerRow/2;winner_column=OutputLayerColumn/2;while(current_iteration_num<total_iteration_Num){//迭代次数控制init_distance();eula_distance();weight_change();if(min_distance<=error_limit) break;++current_iteration_num;paraChange();}iteration_numbers[l]=current_iteration_num+1;neighbor_width=OutputLayerColumn; //修改邻域的宽度neighbor_height=OutputLayerRow; //修改邻域的⾼度study_efficiency=efficiency; //学习率重置current_iteration_num=0; //重置迭代次数min_distance=1000.0; //重置最⼩距离}/***********************************///输出部分/***********************************/for(l=0;l<26;l++) total_num+=iteration_numbers[l];ofstream iteration_num("迭代次数.txt",ios::out);for(l=0;l<26;l++){iteration_num<<character[l]<<"迭代"<<iteration_numbers[l]<<"次!\n"<<endl;if(l==25) iteration_num<<"整个训练过程共迭代"<<total_num<<"次!\n"<<endl;}ofstream all_weight("训练后所有权值.txt",ios::out);ofstream winner_weight("训练后胜出权值.txt",ios::out);for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++){printf("\n\n\n");all_weight<<"\n\n\n"<<"Node["<<i+1<<"]["<<j+1<<"]"<<"\n";for(k=0;k<InputLayerNum;k++){if(k%5==0){printf("\n");all_weight<<"\n";}if(weight[i*OutputLayerColumn+j][k]>0.9999999) weight[i*OutputLayerColumn+j][k]=1.0;if(weight[i*OutputLayerColumn+j][k]<0.0000001) weight[i*OutputLayerColumn+j][k]=0.0;printf("%f ",weight[i*OutputLayerColumn+j][k]);all_weight<<setprecision(8)<<setiosflags(ios::fixed)<<weight[i*OutputLayerColumn+j][k]<<"";}}ofstream winner_node("获胜节点.txt",ios::out);for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++){if(flag[i][j]==100){ //获胜节点printf("\n\n\n");winner_weight<<"\n\n\n"<<"Node["<<i+1<<"]["<<j+1<<"]"<<"\n";for(k=0;k<InputLayerNum;k++){if(k%5==0){printf("\n");winner_weight<<"\n";}if(weight[i*OutputLayerColumn+j][k]>0.9999999) weight[i*OutputLayerColumn+j][k]=1.0;if(weight[i*OutputLayerColumn+j][k]<0.0000001) weight[i*OutputLayerColumn+j][k]=0.0;printf("%f ",weight[i*OutputLayerColumn+j][k]);winner_weight<<setprecision(8)<<setiosflags(ios::fixed)<<weight[i*OutputLayerColumn+j][k]<<""; }winner_node<<"Node["<<i+1<<"]["<<j+1<<"]"<<endl;}}printf("\n");test_netWork_1();test_netWork_2();return0;}void test_netWork_1(){ofstream test1("标准测试.txt",ios::out);char character[26];for(i=0;i<26;i++) character[i]=(65+i);for(l=0;l<26;l++){for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++) distance[i*OutputLayerColumn+j]=0.0;min_distance=1000;for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++){for(m=0;m<7;m++)for(n=0;n<5;n++)distance[i*OutputLayerColumn+j]+=pow(inputMode[l][m][n]-weight[i*OutputLayerColumn+j][m*5+n],2);if(distance[i*OutputLayerColumn+j]<min_distance){min_distance=distance[i*OutputLayerColumn+j];temp_row=i;temp_column=j;}}test1<<character[l]<<"'s winner is Node["<<temp_row+1<<"]["<<temp_column+1<<"]"<<endl<<endl;}}/****************************************************///利⽤⾮标准数据测试训练后的⽹络/****************************************************/void test_netWork_2(){ofstream test2("⾮标准测试.txt",ios::out);char character[26];FILe *pf=fopen("⾮标准数据测试.txt","a+");if(pf==NULL){cout<<"Can not open input file!\n";exit(0);}for(i=0;i<26;i++)for(j=0;j<7;j++)for(k=0;k<5;k++) fscanf(pf,"%d",&inputMode[i][j][k]);for(i=0;i<26;i++) character[i]=(65+i);for(l=0;l<26;l++){for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++) distance[i*OutputLayerColumn+j]=0.0;min_distance=1000;for(i=0;i<OutputLayerRow;i++)for(j=0;j<OutputLayerColumn;j++){for(m=0;m<7;m++)for(n=0;n<5;n++)distance[i*OutputLayerColumn+j]+=pow(inputMode[l][m][n]-weight[i*OutputLayerColumn+j][m*5+n],2);if(distance[i*OutputLayerColumn+j]<min_distance){min_distance=distance[i*OutputLayerColumn+j];temp_row=i;temp_column=j;}}test2<<character[l]<<"'s winner is Node["<<temp_row+1<<"]["<<temp_column+1<<"]"<<endl<<endl;}}。

基于 SOM 算法的聚类分析研究聚类分析是数据挖掘和机器学习领域中的一个重要研究方向，而SOM算法是其中一种经典的聚类方法。

本文我们将从SOM算法的基本原理、应用场景和研究成果等方面，深入探讨SOM算法在聚类分析中的应用。

一、基本原理SOM算法全称为自组织映射（Self-Organizing Map），是由芬兰赫尔辛基理工大学教授Teuvo Kohonen于1980年提出的一种基于无监督学习的神经网络算法。

SOM算法基本思想是将一组高维数据映射到一个低维或二维的输出空间中，使得距离接近的数据点映射到相邻的输出单元中。

SOM算法由输入层、竞争层和输出层构成，其中输入层来自数据集的特征向量，而竞争层和输出层均为拓扑结构，其在输出空间中形成了一个格点。

竞争层中的神经元互相竞争输入向量，最终输出与输入向量最相近的神经元。

在训练过程中，每个输入向量通过与竞争层中神经元的权重进行点乘，得到该神经元对应的输出向量。

竞争过程中，SOM算法中最常用的竞争函数是欧氏距离公式，它的计算公式如下：$\sqrt{\sum_{i=1}^n(w_{i}-x_{i})^2}$其中，w和x分别是竞争层神经元的权重和训练集的输入向量，n是输入向量的维度。

竞争函数的结果越小，则一定程度上说明该输入向量与对应的神经元越相似。

竞争完毕后，输出层将竞争成功的神经元按照拓扑结构重新排列，以此形成一个无监督的聚类分布。

二、应用场景SOM算法被广泛应用于自然语言处理、生物信息学、物联网、图像识别等领域。

具体例子如下：1. 自然语言处理方面，SOM算法已被应用于文本聚类、语音识别等方面。

在文本聚类中，SOM可将文本数据聚类为若干个主题，是一种趋势分析和舆情分析的常用工具。

2. 生物信息学方面，SOM算法已被应用于基因表达数据的聚类分析，帮助生命科学研究者挖掘基因表达的深层次特征。

3. 物联网方面，SOM算法已被应用于传感器数据的聚类，为物联网应用提供更好的数据分析支持。

人工神经网络简介本文主要对人工神经网络基础进行了描述，主要包括人工神经网络的概念、发展、特点、结构、模型。

本文是个科普文，来自网络资料的整理。

一、人工神经网络的概念人工神经网络（Artificial Neural Network，ANN）简称神经网络(NN)，是基于生物学中神经网络的基本原理，在理解和抽象了人脑结构和外界刺激响应机制后，以网络拓扑知识为理论基础，模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。

该模型以并行分布的处理能力、高容错性、智能化和自学习等能力为特征，将信息的加工和存储结合在一起，以其独特的知识表示方式和智能化的自适应学习能力，引起各学科领域的关注。

它实际上是一个有大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。

神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。

每个节点代表一种特定的输出函数，称为激活函数（activation function）。

每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），神经网络就是通过这种方式来模拟人类的记忆。

网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。

而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

神经网络的构筑理念是受到生物的神经网络运作启发而产生的。

人工神经网络则是把对生物神经网络的认识与数学统计模型相结合，借助数学统计工具来实现。

另一方面在人工智能学的人工感知领域，我们通过数学统计学的方法，使神经网络能够具备类似于人的决定能力和简单的判断能力，这种方法是对传统逻辑学演算的进一步延伸。

人工神经网络中，神经元处理单元可表示不同的对象，例如特征、字母、概念，或者一些有意义的抽象模式。

网络中处理单元的类型分为三类：输入单元、输出单元和隐单元。

输入单元接受外部世界的信号与数据；输出单元实现系统处理结果的输出；隐单元是处在输入和输出单元之间，不能由系统外部观察的单元。

神经网络的原理
神经网络是一种模拟人类大脑神经元网络的计算模型，它是一
种机器学习的算法，通过模拟人类神经元之间的连接和传递信息的
方式来进行学习和预测。

神经网络的原理是基于神经元之间的连接
和信息传递，通过不断调整连接权重来实现对输入数据的学习和预测。

在神经网络中，神经元是神经网络的基本单元，它接收来自其
他神经元的输入，并通过激活函数来产生输出。

神经元之间的连接
权重决定了输入信号的重要性，通过不断调整这些连接权重，神经
网络可以学习到输入数据之间的复杂关系，并进行预测和分类。

神经网络的训练过程是通过反向传播算法来实现的，这个算法
通过计算预测值与真实值之间的误差，并将误差通过网络反向传播，来调整每个神经元之间的连接权重，从而不断优化神经网络的预测
能力。

通过大量的训练数据和迭代训练，神经网络可以逐渐提高其
对输入数据的预测准确性。

神经网络的原理可以用于各种领域，比如图像识别、语音识别、自然语言处理等。

在图像识别中，神经网络可以学习到不同特征之
间的关系，从而实现对图像的自动识别和分类；在语音识别中，神经网络可以学习到语音信号的特征，从而实现对语音指令的识别和理解；在自然语言处理中，神经网络可以学习到语言之间的语义和语法关系，从而实现对文本信息的分析和理解。

总的来说，神经网络的原理是基于神经元之间的连接和信息传递，通过不断调整连接权重来实现对输入数据的学习和预测。

神经网络已经在各个领域取得了巨大的成功，未来也将继续发挥重要作用，推动人工智能技术的发展和应用。