数学实验三 MATLAB软件入门(绘图)

柱状图
总结词
用于比较不同类别数据的数值大小。
详细描述
柱状图是一种常用的数据可视化工具，它通过在垂直或水平方向上绘制一系列的柱子，每个柱子代表一个数据类 别，高度或长度表示该类别的数值大小。柱状图可以清晰地展示不同类别之间的数值差异和比较。
饼图
总结词
用于表示各部分在总体中所占的比例。
VS
详细描述
饼图是一种圆形图表，它将一个完整的圆 分割成若干个扇形，每个扇形代表一个数 据类别，扇形的面积或角度表示该类别的 比例大小。饼图可以清晰地展示各部分在 总体中所占的比例和比较。
动画制作
帧动画
通过在连续的帧上绘制图形或改 变图形属性来创建动画效果。
交互式动画
使用鼠标或键盘控制动画的播放 暂停和停止等操作。
运动轨迹
绘制物体在运动过程中的轨迹， 以展示物体的运动规律和特点。
三维图形
三维曲线
在三维空间中绘制曲线，可以展 示不同变量之间的关系和变化趋
势。
三维曲面
通过绘制三维曲面来展示两个或多 个变量之间的关系和分布情况。
函数调用与执行
在主程序中调用自定义函数，执行绘图操作，实现特定图形的绘 制。
数据导入和导
1 2
数据导入
将外部数据文件（如Excel、CSV等格式）导入 Matlab中，用于后续的绘图分析。
数据处理
对导入的数据进行必要的预处理和清洗，以满足 绘图需求。
3
数据导出
将绘制好的图形和数据导出为特定格式（如PNG 、JPEG、PDF等），方便分享和保存。
三维体图
绘制三维体图来展示数据的空间分 布和密度变化，如云图、等高线图 等。
04
实例分析
绘制正弦函数图像

详细描述
MATLAB提供了交互式图形工具，如 `ginput`、`axes_crossing_info`等，使用户 能够与图形进行交互。通过这些工具，用户 可以获取图形的坐标值、筛选数据等操作， 从而更深入地分析数据。交互式图形在数据 探索和可视化方面具有很高的实用价值。
04
实例教程
绘制正弦函数和余弦函数
等，可以提高绘图效率和精度。
实践项目
02
通过实践项目来巩固和加深对MATLAB绘图的理解，例如数据
拟合、图像处理等。
参加在线课程和论坛
03
参加在线课程和论坛，与其他用户交流和学习，可以扩展视野
和知识面。
THANKS
感谢观看
mat制基本图形 • 图形进阶技巧 • 实例教程 • 总结与扩展
01
MATLAB绘图基础
绘图函数简介
bar()
绘制条形图，用于 展示分类数据或离 散数据。
hist()
绘制直方图，用于 展示数据的分布情 况。
plot()
绘制二维线图，是 MATLAB中最常用 的绘图函数。
05
总结与扩展
MATLAB绘图的优势与不足
强大的数据处理能力
MATLAB提供了丰富的数据处理函数，方便 用户进行数据分析和可视化。
丰富的图形样式
MATLAB支持多种图形样式，包括散点图、 线图、柱状图等，可以满足各种绘图需求。
MATLAB绘图的优势与不足
• 交互式绘图：MATLAB支持交互式绘图，用户可以通过鼠 标操作对图形进行缩放、旋转等操作。
```
绘制饼状图
在此添加您的文本17字
总结词：饼状图用于展示各类别数据在总数据中所占的比 例。
在此添加您的文本16字

plotyy(x1,y1,x2,y2)
其中x1—y1对应一条曲线，x2—y2对应 另一条曲线。横坐标的标度相同，纵坐 标有两个，左纵坐标用于x1—y1数据对， 右纵坐标用于x2—y2数据对。
精品课件
目录 17
例4.4 用不同标度在同一坐标内绘制曲线 y1=e-0.5xsin(2πx)
及曲线y2=1.5e-0.1xsin(x)。 程序如下：
x1=(0:12)/2;
y3=2*exp(-0.5*x1).*sin(2*pi*x1);
plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');
目录
精品课件
16
4．双纵坐标函数plotyy
plotyy函数是MATLAB 5.X新增的函数。 它能把函数值具有不同量纲、不同数量 级的两个函数绘制在同一坐标中。调用 格式为：
plot(x,y) 其中x和y为长度相同的向量，分别用于存储x坐
标和y坐标数据。条件是元素个数能对应。
精品课件
目录 4
例4.1 在0≤X≤2区间内，绘制 曲线y=2e-0.5xsin(2πx)。
程序如下：>> x=0:pi/100:2*pi;
y=2*exp(-0.5*x).*sin(2*pi*x); plot(x,y)
可搭配使用，如选项“ro” 表示绘制红色的圆划线，“y-”表
示黄色的实划线。
精品课件
14
例 用不同线型和颜色在同一坐标内绘制曲 线y=sinx,y=cosx的图像。
程序如下：
x=linspace(0,2*pi,100); plot(x,sin(x),‘kh’,x,cos(x),‘gp’) %正、余弦曲

clf;dx=0.1;x=0:dx:4;y=x.*sin(x);s=cumtrapz(y)*dx; sint='{\fontsize{16}\int_{\fontsize{8}0}^{ x}}';
plotyy(x,y,x,s),text(0.5,0,'\fontsize{14}\ity=xsinx') text(2.5,3.5,['\fontsize{14}\its=',sint,'\fontsize{14}\itxsinxdx'])
运行图像：
2/3 exp(-1/2 t) cos(1/2 31/2 t) 0.55 0.5 0.1 0.45 0.4 0.35 0 0.3 0.25 0.2 -0.1 0.15 0 5 10 0 5 10 s = y(t)dt
0.15
0.05
-0.05
t
t
7、编写 MATLAB 程序，画五角星
输入程序：n=1:2:11; x=sin(0.4*n*pi); y=cos(0.4*n*pi); plot(x,y) 输出图像： axis([-1,1,-1,1]),axis square
输出图像
helix
40 30 20 10 0 1 0.5 0 -0.5 -1 -1 -0.5 0
origin 0.5 1
9、用MATLAB绘制饼图
输入程序：function shi h0=figure('toolbar','none', 'position',[200 150 450 250],'name'); t=[54 21 35; 68 54 35; 45 25 12; 48 68 45; 68 54 69]; x=sum(t); h=pie(x); textobjs=findobj(h,'type','text'); str1=get(textobjs,{'string'}); val1=get(textobjs,{'extent'}); oldext=cat(1,val1{:});

Matlab 软件实习
5. 分块绘图
分块绘图函数: subplot(m,n,p) 其作用为将图形窗口分割为m行n列的子窗口,然后选定 第p号子窗口为当前窗口.
Matlab 软件实习
例12: 将函数y1=sin(x) , y2=cos(x), y3=x2, y4=ex分块绘制在
同一窗口.
程序如下: subplot(2,2,1) fplot(‘sin(x)’,[-pi,pi],’r’) title(‘sin(x)’) subplot(2,2,2) fplot(‘cos(x)’,[-pi,pi],’m’) title(‘cos(x)’) subplot(2,2,3) fplot(‘x^2’,[-2,2],’.-’) title(‘x^2’) subplot(2,2,4) fplot(‘exp(x)’,[-3,3],’k’) title(‘exp(x)’)
据对,右纵坐标用于x2,y2数据对.
Matlab 软件实习
例5: 用不同标度在同一坐标内绘制曲线 y1=0.2e-0.5xcos(4x) 和 y2=2e-0.5xcos(x). 程序如下： x=0:pi/100:2*pi; y1=0.2*exp(-0.5*x).*cos(4*pi*x); y2=2*exp(-0.5*x).*cos(pi*x); plotyy(x,y1,x,y2);
每一向量对可以绘制出一条曲线,这样可以在同一坐标
内绘制出多条曲线.
② 当输入参数有矩阵形式时,配对的x,y按对应列元
素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列 数.
Matlab 软件实习
例3: 绘制曲线. 程序如下： x1=0:0.1:2*pi; x2=1:0.1:3*pi; plot(x1,sin(x1),x2,cos(x2));

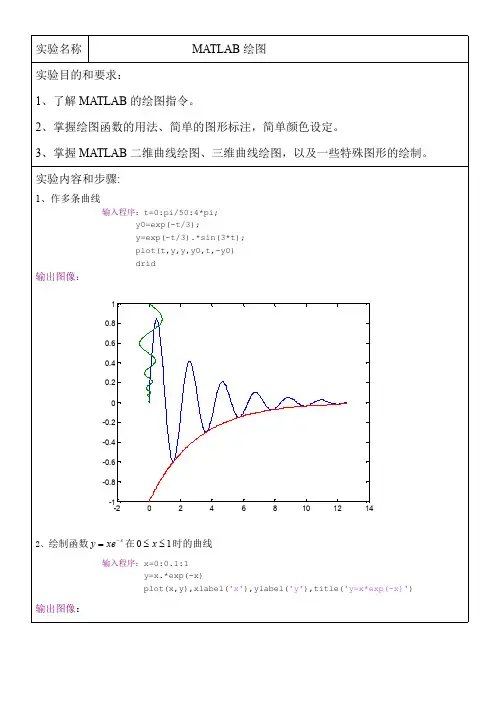
实验2 Matlab 绘图操作
实验目的：
1、 掌握绘制二维图形的常用函数；
2、 掌握绘制三维图形的常用函数；
3、 掌握绘制图形的辅助操作。

实验内容：
1. 设sin .cos x y x x ⎡⎤
=+⎢⎥+⎣
⎦23051，在x=0~2π区间取101点，绘制函数的曲线。

2. 已知： y x =21，cos()y x =22，y y y =⨯312，完成下列操作：
（1） 在同一坐标系下用不同的颜色和线性绘制三条曲线；
（2） 以子图形式绘制三条曲线；
（3） 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。

3.
已知：ln(x y x x ≤=⎨⎪+>⎪⎩0102
，在x -≤≤55区间绘制函数曲线。

4. 绘制极坐标曲线sin()a b n ρθ=+，并分析参数a 、b 、n 对曲线形状的影响。

5．在xy 平面内选择区域[][],,-⨯-8888，
绘制函数z =的三种三维曲面图。

6. 用plot 函数绘制下面分段函数的曲线。

,(),,x x f x x x x ⎧++>⎪==⎨⎪+-<⎩235000
50
7. 某工厂2005年度各季度产值（单位：万元）分别为：450.6、395.9、410.2、450.9，试绘制柱形图和饼图，并说明图形的实际意义。

8. 在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。

（1）.y x =-205
（2）sin()cos ,sin()sin x t t t y t t π=⎧≤≤⎨=⎩303。

Note: （1） fun为函数名，以字符串形式出现。lims为变量取 值范围，tol为相对允许误差，其系统默认值为2e-3。 （2） fun必须是M文件的函数名或是独立变量为x的字 符串. （3） fplot函数不能画参数方程和隐函数图形，但在一 个图上可以画多个图形.
【例】 在[-2,2]范围内绘制函数tanh的图形.
最基本的三维图形函数为plot3，它是将二维函数plot 的有关功能扩展到三维空间，用来绘制三维图形。
Plot3 ( x,y,z,c)
Note：函数功能：以向量x，y，z为坐标，绘制三维曲 线，其中x,y,z表示三维坐标向量，表示线形或颜色。
4.4 三维图形
【例】 绘制三维螺旋曲线：
t=0:pi/50:10*pi; y1=sin(t),y2=cos(t); plot3(y1,y2,t); title('helix'); text(0,0,0,‘origin’); %在(0,0,0)点添加文本框 xlabel('sin(t)'),ylabel('cos(t)'),zlabel('t');
4.3 其它图形函数
3、填充图形
fill(x,y,’c’) — 绘制并填充二维多边图形
Note：x和y为二维多边形顶点坐标向量。字符 ’c’ 规 定填充颜色，其取值前已叙述。
如：绘制一正方形并以黄色填充： x=[0 1 2 4 0]; %正方形顶点坐标向量 y=[0 0 1 1 0]; fill(x,y,‘b’) %绘制并以蓝色填充正方形图
Note:表示在区间tmin<t<tmax绘制参数方程 x=x(t), y=y(t)的函数图.
【例】 在[0, 2 ]π上画 y sin3 t 的x星形co图s3 t.

[X, Y] = meshgrid(-3:0.1:3);
Z = griddata(x, y, z, X, Y, 'cubic'); mesh(X, Y, Z);
hold on
plot3(x, y, z, '.', 'MarkerSize', 16);
% 晝出 100 個取樣
hold off
axis tight
4-1 基本立體繪圖指令
waterfall：
waterfall 指令可在 x 方向或 y 方向產生水流 效果
範例4-7：plotxyz04.m
[x, y, z] = peaks; waterfall(x,y,z); axis tight;
4-1 基本立體繪圖指令
範例4-7：plotxyz04.m
4-1 基本立體繪圖指令
範例4-3 ：plotxyz011.m
x = 3:6; y = 5:9; [xx, yy] = meshgrid(x, y); zz = xx.*yy; subplot(2,2,1); mesh(xx); title('xx'); axis tight subplot(2,2,2); mesh(yy); title('yy'); axis tight subplot(2,2,3); mesh(xx, yy, zz); title('zz 對 xx 及 yy 作圖'); axis tight
允許（on）或不允許（off）指令視 窗的輸出暫停。
允許（on）或不允許（off）指令在 檔案內執行時，逐一顯示在視窗。
4-2 立體圖形與圖軸的基本技巧
rotate3d on：

四、MATLAB三维曲面绘图

meshgrid——生成网格矩阵 调用格式：

[X,Y]=meshgrid(x,y)--------生成小矩形顶点的坐
标值矩阵

[X,Y]=meshgrid(x) 等价于[X,Y]=meshgrid(x,x)
例:x=[1,2,3]；y=[1,2,3,4]； [X,Y]=meshgrid(x,y)

xlabel(‘String’)
在当前图形的x轴旁边加入文字内容
ylabel(‘String’)
zlabel(‘String’)
在当前图形的y轴旁边加入文字内容
在当前图形的z轴旁边加入文字内容

图形标注gtext

gtext(‘String’)
在鼠标指定位置上标注
说明：使用gtext指令后，会在当前图形上出现一个十字 叉，等待用户选定位置进行标注。移动鼠标到所需位置按 下鼠标左键，Matlab就在选定位置标上文字。
马鞍面、平面及交线
练习： 二维曲线4-4，4-5 p42 例4-9 p47 例4-11，4-12
三维曲线：
p57 例4-22,4-23,4-24
三维曲面：
p60 例4-26,4-28,4-29,4-30

作业：P79 3,5,9
x=[1 2 3]; y=[3 3 1 473 581 4 4 4] plot(x,y)

plot3与plot的 用法相同
，
x t sin t 例：绘制三维曲线的图像： y t cos t z t
解：matlab命令为：
(0 t 20 )
t=0:pi/10:20*pi; x=t.*sin(t); y=t.*cos(t) ; z=t; plot3(x,y,z)

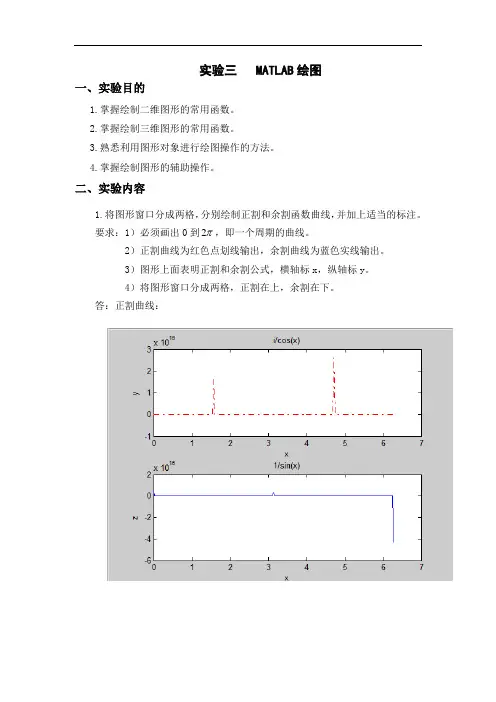
实验三 MATLAB绘图一、实验目的1.掌握绘制二维图形的常用函数。

2.掌握绘制三维图形的常用函数。

3.熟悉利用图形对象进行绘图操作的方法。

4.掌握绘制图形的辅助操作。

二、实验内容1.将图形窗口分成两格，分别绘制正割和余割函数曲线，并加上适当的标注。

要求：1）必须画出0到 2，即一个周期的曲线。

2）正割曲线为红色点划线输出，余割曲线为蓝色实线输出。

3）图形上面表明正割和余割公式，横轴标x，纵轴标y。

4）将图形窗口分成两格，正割在上，余割在下。

答：正割曲线：程序截图：2.将图形窗口分成两个窗格，分别绘制出函数：1352221+-=+=x x y x y在[0,3]区间上的曲线，并利用axis 调整轴刻度纵坐标刻度，使1y 在[0,12]区间上，2y 在[-2,1.5]区间上。

解：曲线截图：程序截图：3.用曲面图表现函数22y x z +=,x 和y 的范围从-4到4，设置当前图形的颜色板从黑色到暗红、洋红、黄色、白色的平滑变化，打开网格。

解：曲面图截图：程序截图：4.（1）先建立一个图形窗口，使之背景色为红色，窗口标题为你的学号和姓名，标题前缀没有”Figure No .1”字样，并在窗口上保留原有的菜单项;（2）在所建立的图形窗口中用默认属性绘制曲线22x，然后通过图y x e形句柄操作来改变曲线的颜色、线型和线宽，并利用文字对象给曲线添加文字标注。

解：（1）截图：程序截图：（2）默认属性下的曲线截图：程序截图：利用句柄、文字对象改变曲线的截图：程序截图：5. 生成一个圆柱体（可用cylinder函数），并进行光照和材质处理。

解：圆柱体截图：程序截图：。

幂运算可按元素对元素方式进行，不同大小或维数 的数组是不能进行运算的.
设：a=[a1,a2,…,an], b=[b1,b2,…,bn] 则：a+b= [a1+b1,a2+b2,…,an+bn]
a.*b= [a1*b1,a2*b2,…,an*bn]
a./b= [a1/b1,a2/b2,…,an/bn]
MATLAB(fun)
返回
二、数 组
MATLAB(shuzu1)
1. 创建简单的数组 x=[a b c d e f]创建包含指定元素的行向量.
x=first：last
创建从first开始，加1计数，到last结束的行向量.
x=first：increment：last
创建从first开始，加increment计数，到last结束的 行向量.
while (expression) {commands}
end
只要在表达式(expression)里的所有元素为真，就执行 while和end语句之间的命令串{commands}.
例 设银行年利率为11.25%.将10000元钱存入银行，问 多长时间会连本带利翻一番？
MATLAB(while1)
3. if-else-end结构 （1）有一个选择的一般形式是：
MATLAB(shuzu2)
3. 数组的方向
前面例子中的数组都是一行数列，是行方向分布的. 称之为行向量. 数组也可以是列向量，它的数组操作和运 算与行向量是一样的，唯一的区别是结果以列形式显示.
产生列向量有两种方法： 直接产生 例 c=[1；2；3；4] 转置产生 例 b=[1 2 3 4]; c=b′
后将该点集的坐标传给MATLAB函数画图.

实验（六）项目名称：三维绘图一、实验目的：熟悉MATLAB中几个常用的绘图命令，掌握集中常见三维图形的画法。

二、实验原理三维绘图命令：Plot（X,Y,Z）//曲线；mesh(X,Y,Z)//网状；surf(X,Y,Z)//表面；contour(X,Y,Z)//等高线。

三、实验环境1.硬件：PC机2. 软件：Windows操作系统、matlab2015四、实验内容、步骤以及结果4.1.1实验要求：用plot函数画出的三维曲线。

4.1.2实验步骤（1）启动matlab，新建一个M文件；（2）输入程序，如图1；（3）保存文件；（4）编译源程序，观察屏幕上显示的编译信息，修改出现的错误，直到编译成功；图1：plot函数画三维曲线4.1.3运行结果如下：图2：三维曲线4.2.1实验要求：用mesh函数画出的三维网状图。

4.2.2实验步骤（5）启动matlab，新建一个M文件；（6）输入程序，如图3；（7）保存文件；（8）编译源程序，查看运行结果，如图4。

图3：mesh函数画三维网状图图4：运行结果4.3.1实验要求：用surf函数画出的三维表面图。

4.3.2实验步骤（9）启动matlab，新建一个M文件；（10）输入程序，如图5；（11）保存文件；（12）编译源程序，查看运行结果，如图6。

图5：surf函数画三维表面图图6：运行结果4.3.1实验要求：用contour函数画出的等高线图。

4.3.2实验步骤（13）启动matlab，新建一个M文件；（14）输入程序，如图7；（15）保存文件；（16）编译源程序，查看运行结果，如图8。

图7：contour函数画等高线图8：运行结果五、实验总结MATLAB具有强大的图形功能，能够将它们直观的表现出来，解决很多的问题。

实验三 MATLAB 绘图一、实验目的1．掌握二维图形的绘制。

2．掌握图形的标注3．了解三维曲线和曲面图形的绘制。

二、实验的设备及条件计算机一台（带有以上的软件环境）。

设计提示1．Matlab 允许在一个图形中画多条曲线：plot(x1，y1，x2，y2，……)指令绘制y 1 = f 1(x 1), y 2 = f 2 (x 2 )等多条曲线。

Matlab 自动给这些曲线以不同颜色。

标注可用text 函数。

2．绘图时可以考虑极坐标和直角坐标的转换。

3．三维曲线绘图函数为plot3，注意参考帮助中的示例。

三、实验内容1．生成1×10 维的随机数向量a ，分别用红、黄、蓝、绿色绘出其连线图、杆图、阶梯图和条形图，并分别标出标题“连线图”、“杆图”、“阶梯图”、“条形图”。

2、绘制函数曲线，要求写出程序代码。

(1) 在区间[0:2π]均匀的取50个点，构成向量t(2) 在同一窗口绘制曲线y1=sin(2*; y2=3cos(t+；要求y1曲线为红色点划线，标记点为圆圈；y2为蓝色虚线，标记点为星号。

(3) 分别在靠近相应的曲线处标注其函数表达式。

3.将图形窗口分成两个绘图区域，分别绘制出函数：⎩⎨⎧+-=+=1352221x x y x y 在[0,3]区间上的曲线，并利用axis 调整轴刻度纵坐标刻度，使1y 在[0,12]区间上，2y 在[-2,]区间上。

4．用mesh 或surf 函数，绘制下面方程所表示的三维空间曲面，x 和y 的取值范围设为[-3，3]。

101022y x z +-=思考题：1. 编写一个mcircle(r)函数，调用该函数时，根据给定的半径r ，以原点为圆心,画一个如图所示的红色空心圆。

（图例半径r=5）；左图参考polar函数的用法，右图绘制圆形的参数方程为x=sin （t ），y=cos （t ）。

其中，t 的区间为0~2*pi ，步长为。

2．（1）绘一个圆柱螺旋线（形似弹簧）图。

提示：可用命令polar 。

3） 空间曲线：(4sin 20)cost,(4sin 20)sint,(020)cos 20,x t y t t z t ⎧=+⎪=+≤≤⎨⎪=⎩； 4） 环面：⎪⎩⎪⎨⎧=+=+=,sin ,sin )cos 1(,cos )cos 1(u z v u y v u x )2,0()2,0(ππ∈∈v u 。

4．建立一个命令M-文件：求所有的“水仙花数”，所谓“水仙花数”是指一个三位数，其各位数字的立方和等于该数本身。

例如，153是一个水仙花数，因为153=13+53+33。

二、实验过程1、1)、实验源代码：syms x;y=(x-1)^7;x=linspace(0.988,1.012,50);y1=subs(y,x);plot(x,y1);syms x;y=expand((x-1)^7);x=linspace(0.988,1.012,50);y2=subs(y,x);plot(x,y2);2）、实验结果及分析：左图为y1的图像，右图为y2的图像，可看出两图有明显的差别，右图为一条连续的曲线，左图则为上下波动的折线，之所以产生这样的差别，应该是分成多项式后，每一项的运算都会损失一些精度，所以最后结果精度损失很大，所以图像就显得不平滑了。

2、1）、实验源代码:x=linspace(-3,3,200);y1=exp(x);plot(x,y1);hold on;y2=1+x;plot(x,y2,'y');y3=1+x+(x.^2)/2;plot(x,y3,'b');y4=1+x+(x.^2)/2+(x.^3)/6;plot(x,y4,'r');title('泰勒公式的验证');legend('y1=e^x','y2=1+x','y3=1+x+(1/2)x^2','y4= 1+x+(1/2)x2+(1/6)x^3') hold off;2）、实验结果及分析：由图像可得，当函数相加的项越多，函数图像越趋近于e^x，由此可验证泰勒公式。

实验四 基本绘图练习一．实验目的和要求1．熟悉Matlab 强大的图形处理功能；2．掌握应用Matlab 实现二维图形和三维图形的绘制和控制与表现方法。

二．实验器材计算机、MATLAB 软件三．实验数据和要求1、y1=sin(x)（02x π≤≤），y2=cos(x) （02x π≤≤），等间隔取100个数据点，在同一个图形窗口中分别绘制以下曲线：(1) 用钻石符号标记数据点的红色实线画y1曲线；(2) 用五角星符号标记数据点的蓝色虚线画y2曲线；(3) 标注图名“sin()β和cos()β的曲线”(5) 标注两条曲线分别为“sin()β”、“cos()β”(6) 标注x 轴“β”，标注y 轴“sin()β和cos()β”(7) 利用鼠标拖动完成标注“ →”(8) 对图形添加网格x=0:pi/100:2*pi; %生成200个数作为数据点y1=sin(x);y2=cos(x); %生成函数y1,y2figure(1);plot(x,y1,'r-d',x,y2,'b--*'); %画y1,y2关于x 的函数图像 grid on; %给图像的背景添加栅格legend('sin(beta)','cos(beta)'); %标注图例text(pi,0,'\leftarrow sin(\beta)');gtext('cos(\beta)\rightarrow'); %用鼠标定位文字title('sin(beta)和cos(beta)'); %标出图名xlabel('\beta');ylabel('sin(\beta)和cos(\beta)')2、某城市1月到6月生产总值(单位为：亿元)数据分别为：170、120、180、200、190、220，试完成以下功能：(1)在2个图形窗口中分别绘制出各月生产总值占前6月总值的二维、三维百分比图形。

实习报告课程名称多媒体实验实习题目基本图形绘制实验专业通信工程班级08通信（2）班学号学生姓名实习成绩指导教师吴娱2011年4月基本图形绘制实验一、实验目的：1、掌握MATLAB的基本绘图函数。

2、掌握绘图函数的用法、简单图形标注、简单颜色设定。

二、实验要求：独立进行实验，完成实验报告。

三、实验内容：1、MATLAB简介：MATLAB语言丰富的图形表现方法，使得数学计算结果可以方便地、多样性地实现了可视化，这是其它语言所不能比拟的。

2、MATLAB的绘图功能：（1）二维绘图：A、plot——最基本的二维图形指令：1. 单窗口单曲线绘图；2. 单窗口多曲线绘图；3. 单窗口多曲线分图绘图；4. 多窗口绘图；5.可任意设置颜色与线型；6.图形加注功能；7.fplot——绘制函数图函数；8.ezplot——符号函数的简易绘图函数B、fill——基本二维绘图函数：绘制二维多边形并填充颜色C、(选做)特殊二维绘图函数：bar——绘制直方图；polar——绘制极坐标图；hist——绘制统计直方图；stairs——绘制阶梯图；stem——绘制火柴杆图；rose——绘制统计扇形图；comet——绘制彗星曲线；errorbar——绘制误差棒图；compass——复数向量图(罗盘图)；feather——复数向量投影图(羽毛图)；quiver——向量场图；area——区域图；pie——饼图；convhull——凸壳图；scatter——离散点图。

（2）三维绘图：A、三维线图：plot3——基本的三维图形指令B、三维网格图：mesh——三维网线绘图函数C、三维表面图：surf——三维曲面绘图函数，与网格图看起来一样D、三维轮廓图：contour——三维轮廓绘图函数E、三维混合图：surfc——三维混合绘图函数四、作业：1、(1)在同一幅图上的（-pi，pi）区间，用0.5的间隔绘制sinx的红色曲线，用0.1的间隔绘制sin(x+0.5)的绿色曲线，用0.01的间隔绘制sin(x+1)的蓝色曲线。

实验目的1．掌握MATLAB的基本绘图命令。

2．掌握运用MATLAB绘制一维、二维、三维图形的方法。

3．给图形加以修饰。

一、预备知识1．基本绘图命令plotplot绘图命令一共有三种形式：⑴plot(y)是plot命令中最为简单的形式，当y为向量时，以y的元素为纵坐标，元素相应的序列号为横坐标，绘制出连线；若y为实矩阵，则按照列绘出每列元素和其序列号的对应关系，曲线数等于矩阵的列数；当y为复矩阵时，则按列以每列元素的实部为横坐标，以虚部为纵坐标，绘出曲线，曲线数等于列数。

⑵ plot(x,y,[linspec])其中linspec是可选的，用它来说明线型。

当x和y为同维向量时，以x为横坐标，y为纵坐标绘制曲线；当x是向量，y是每行元素数目和x维数相同的矩阵时，将绘出以x为横坐标，以y中每行元素为纵坐标的多条曲线，曲线数等于矩阵行数；当x为矩阵，y为相应向量时，使用该命令也能绘出相应图形。

⑶plot(x1,y1,x2,y2,x3,y3……)能够绘制多条曲线，每条曲线分别以x和y为横纵坐标，各条曲线互不影响。

线型和颜色MATLAB可以对线型和颜色进行设定，线型和颜色种类如下：线：—实线：点线—.虚点线——折线点：.圆点 +加号 *星号 x x型 o 空心小圆颜色：y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1] 直方图在实际中，常会遇到离散数据，当需要比较数据、分析数据在总量中的比例时，直方图就是一种理想的选择，但要注意该方法适用于数据较少的情况。

直方图的绘图函数有以下两种基本形式。

·bar(x,y) 绘制m*n 矩阵的直方图。

其中y 为m*n 矩阵或向量，x 必须单向递增。

·bar(y) 绘制y 向量的直方图，x 向量默认为x=1:m close all; %关闭所有的图形视窗。

x=1:10;y=rand(size(x)); bar(x,y); %绘制直方图。