2020/6/16
《集合论与图论》第17讲
27
作业(#13)
p234, 习题八, 2,3,4(更正: G-v0)
2020/6/16
《集合论与图论》第17讲
28
欧拉回路(Euler tour/circuit): 经过图中所 有边的简单回路
欧拉图(Eulerian): 有欧拉回路的图 半欧拉图(semi-Eulerian): 有欧拉通路的
图
2020/6/16
《集合论与图论》第17讲
5
无向欧拉图的充分必要条件
定理1: 设G是无向连通图,则 (1) G是欧拉图
2020/6/16
《集合论与图论》第17讲
10
有向半欧拉图的充分必要条件
定理4: 设G是无向连通图,则 (1) G是半欧拉图
(2) G中恰有2个奇度顶点, 其中1个入度 比出度大1,另1个出度比入度大1, 其余顶 点入度等于出度. #
2020/6/16
《集合论与图论》第17讲
11
例
2020/6/16
17
Fleury算法(正确性证明)
定理5: 设G是无向欧拉图,则Fleury算法 终止时得到的简单通路是欧拉回路
证明: (1) Pm是回路: 显然. (2) Pm经过G中所有边: (反证)否则,
G-Pm的连通分支还是欧拉回路, 并且与 Pm相交. 若v0是交点,则算法不应结束; 若 v0不是交点,则算法在最后离开交点回到 v0时走了桥; 这都是矛盾! #
24
中国邮递员问题(解法)
解法: (1) 求带权图G所有奇数顶点之间的短程线 (2) 用所有奇数顶点和短程线得完全图K (3) 求K的最小完美匹配M (4) 用M给G沿短程线加重复边得G* (4) 求G*的欧拉回路
2020/6/16
《集合论与图论》第17讲
25
中国邮递员问题(举例)
A2 B1 C1 D2 E
《集合论与图论》第17讲
13
Fleury算法
输入: 连通图G,起点v,终点w. 若vw, 则除 v,w外的顶点都有偶数度;若v=w, 则所有 顶点都有偶数度.
输出: 从v到w的欧拉通路/欧拉回路. 算法: (下一页)
2020/6/16
《集合论与图论》第17讲
14
Fleury算法(递归形式)
{e1,e2 ,… ,ei}, ei+1:= Gi中满足如下2条件的边: (a) ei+1与vi关联 (b) 除非别无选择,否则ei+1不是Gi中的桥 (3) 若GiNi, 则回到(2); 否则算法停止
2020/6/16
《集合论与图论》第17讲
16
Fleury算法(举例)
2020/6/16
《集合论与图论》第17讲
2020/6/16
《集合论与图论》第17讲
8
无向半欧拉图的充分必要条件
定理2: 设G是无向连通图,则 (1) G是半欧拉图
(2) G中恰有2个奇度顶点 证明: (1)(2): 欧拉通路的起点和终点是
奇数度,其余顶点都是偶数度. (2)(1): 在两个奇数度顶点之间加1条新边,
所有顶点都是偶数度,得到欧拉回路.从欧 拉回路上删除所加边后,得到欧拉通路. #
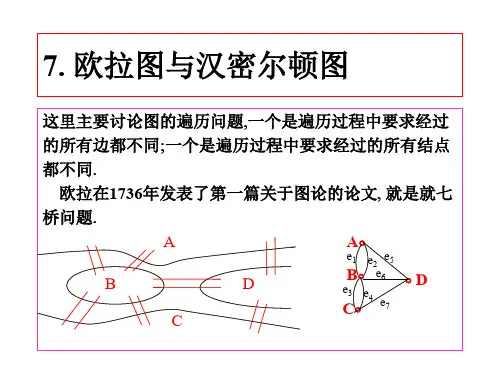
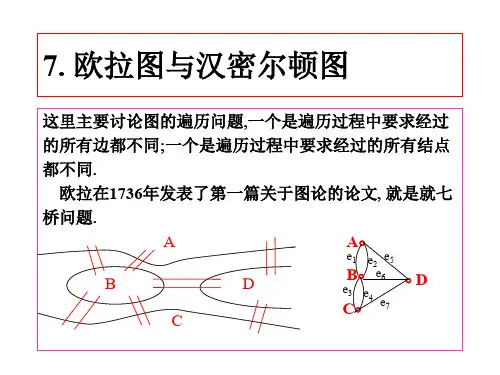
第17讲 欧拉图
1. 七桥问题,一笔画,欧拉通(回)路,欧拉图 2. 判定欧拉图的充分必要条件 3. 求欧拉回路的算法 4. 中国邮递员问题
2020/6/16
《集合论与图论》第17讲
1
一笔画
2020/6/16
《集合论与图论》第17讲
4
欧拉图(Eulerian)
欧拉通路(Euler trail): 经过图中所有边的 简单通路
else Gi+1:=G-E(Pi+1), e:=Gi+1中与Pi+1上vk关联的任意边, Pi+1:= vk…vk. v*:=vk,v:=vk, i:=i+1, goto (1).
2020/6/16
《集合论与图论》第17讲
19
逐步插入回路算法(举例)
2020/6/16
《集合论与图论》第17讲
20
(2) G中所有顶点都是偶数度 (3) G是若干个边不交的圈的并 证明: (1)(2)(3)(1). (1)(2): 若欧拉回路总共k次经过顶点v,则
d(v)=2k.
2020/6/16
《集合论与图论》第17讲
6
定理1((2)(3))
(2) G中所有顶点都是偶数度 (3) G是若干个边不交的圈的并 证明: (2)(3): 若删除任意1个圈上的边,
101 011
11
100 10
110
1
11
1
0
0
0
1
1
00
2020/6/16
111
《集合论与图论》第17讲
22
中国邮递员问题
中国邮递员问题(Chinese postman problem): 求邮递员走遍管区所有街道的 最短回路
管梅谷(Guan Mei-gu),1962,中国 运筹学(Operation Research) 组合优化(Combinatorial Optimization)
G1
6
5
3
I 2H
4
G2 F
B2 K5 8
H4
D 57
G
A2 B1 C1 D2 E
G* 1
6
5
3
I 2H
4
G2 F
最优路线: ABCDEFGHBCDGHIA, W(G*)=35
2020/6/16
《集合论与图论》第17讲
26
总结
七桥问题,一笔画,欧拉通(回)路,欧拉图 判定欧拉图的充分必要条件 求欧拉回路的算法 中国邮递员问题
2020/6/16
《集合论与图论》第17讲
9
有向欧拉图的充分必要条件
定理3: 设G是有向连通图,则 (1) G是欧拉图
(2) vV(G), d+(v)=d-(v) (3) G是若干个边不交的有向圈的并 证明: (1)(2)(3)(1). (1)(2): 若欧拉回路总共k次经过顶点v,则
d+(v)=d-(v)=k. 其余与定理1类似. #
《集合论与图论》第17讲
12
算法(algorithm)
一组有限条指令, 具有以下特征:
输入: 算法工作对象 输出: 算法工作结果 确定性: 算法根据输入和当前工作状态, 决定
下一步采用的指令 可行性: 算法的指令都是可以实现的 终止性: 算法工作有穷步后停止
输入
指令组 工作区
输出
2020/6/16
2020/6/16
《集合论与图论》第17讲
18
逐步插入回路算法
(0) i:=0, v*:=v,v:=v1,P0=v1, G0=G. (1) e:=在Gi中与v关联的任意边(v,v’),
Pi+1:=“Pi”ev’. (2) if v’v* then i:=i+1, v=v’, goto (1). (3) if E(Pi+1)=E(G) then 结束
算法:
(1) if d(v)>1 then e:=v关联的任意非割边
(2)
else e:=v关联的唯一边
(3) u:=e的另一个端点.
(4) 递归地求G-e的从u到w的欧拉通路
(5) 把e接续在递归地求出的通路上
2020/6/16
《集合论与图论》第17讲
15
Fleury算法(迭代形式)
算法:
(1) P0:=v; (2) 设Pi=v0e1v1e2…eivi已经行遍,设Gi=G-
应用(轮盘设计)
000,001,010,011,100,101,110,111
ba c
2020/6/16
a
1
0
c11Fra bibliotek0《集合论与图论》第17讲
1 0 1
21
应用(轮盘设计)
D=<V,E>, V={00,01,10,11}, E={ abc=<ab,bc> | a,b,c{0,1} }
000
00 001 01 010
2020/6/16
《集合论与图论》第17讲
23
带权图(weighted graph)
带权图(weighted graph): G=<V,E,W>,
W:ER, W(e)称为e的权
B5 C
3
5
A 8 14 10
D
B5 C
3
5
A 8 14 10
D
4
9
4
9
F6 E
F6 E
13
2020/6/16
《集合论与图论》第17讲
则所有顶点的度还是偶数, 但是不一定连 通了. 对每个连通分支重复进行.
2020/6/16
《集合论与图论》第17讲
7
定理1((3)(1))
(1) G是欧拉图 (3) G是若干个边不交的圈的并 证明: (3)(1): 有公共点但边不交的简单
回路, 总可以拼接成欧拉回路: 在交点处, 走完第1个回路后再走第2个回路. # 用归纳法严格证明
