六年级下册数学组合图形练习题

12.平面组合图形1.正方形ABCD的边长为8厘米，三角形ABC三角形CEF的面积大10平方厘米，求阴影部分的面积。

2.如图，两图中的两个圆的半径都是5厘米，两个图中阴影部分的面积相比较，（）。

A.图①大B.图②大C.一样大3.如图，小圆的半径是1厘米，大圆的半径是5厘米，小圆沿着大圆外延滚动直至回到起点位置，（1）小圆扫过的面积是多少平方厘米？（2）小圆圆心经过的长度是多少厘米？（3）小圆一共转了多少圈？4.如图，正方形中阴影部分的面积是53c㎡，那么正方形的面积是多少平方厘米？5.墙角O点处的一木桩上栓着一只羊（如图）,栓羊的绳子长4米，墙角两边的墙长2米。

这只羊能吃到草的面积最多是多少？6.如图，已知一个五边形的三条边的长和四个角,试求这个五边形的面积。

（单位厘米）7.如图在大正方形中，三个涂色部分图形周长的和是60厘米，大正方形的面积是多少平方厘米？8.在一个底面是长方形的洗脸盆中，有一个直径6厘米的圆形塑料片在盆地任意滑动。

这个塑料片不可能滑到的面积是多少平方厘米？9.下图中空白部分是一个正方形，求阴影部分的周长和面积。

10.求图中阴影部分的面积，其中A为边的中点。

（单位：cm）11.如图，大正方形的边长比小正方形的长2厘米，小正方形的面积比大正方形小36平方厘米。

小正方形的面积是（）平方厘米。

12.如图，大、小两个正方形中阴影部分的面积比是3：1，小正方形的面积是大正方形的( )。

13.已知右图中长方形被分成四部分，三角形BCO的面积是4cm²，三角形CDO 的面积是8cm²，涂色部分的面积是（）cm²。

14.如图，涂色部分的面积是10平方厘米，空白部分的面积是多少平方厘米。

15.正方形的面积是12平方厘米，求阴影部分的面积。

参考答案1.222.B3. 24π、12π、54.1005.6π6.187.1448.7.749.21.42、10.2610.9π11.6412.1 913.2014.52.815.3π详细讲解，请参阅“小学六年级数学思维提升培优拓展题讲解之《12平面组合图形》”。

六年级数学组合图形的面积试题答案及解析1.我们开始提到的“乡村小屋”的面积是多少？【答案】18【解析】图形内部格点数；图形边界上的格点数；根据毕克定理，则(单位面积)．2.两个边长相等的正方形各被分成25个大小相同的小方格．现将这两个正方形的一部分重叠起来，若左上角的阴影部分(块状)面积为，右下角的阴影部分(线状)面积为，求大正方形的面积．【答案】19【解析】块状部分与线状部分之间的部分称为D，则D与前者共14个方格，与后者共17个方格，因此每个方格的面积是大正方形的面积为．3.如图，平行四边形，，，，，平行四边形的面积是，求平行四边形与四边形的面积比．【答案】1/18【解析】连接、．根据共角定理∵在和中，与互补，∴．又，所以．同理可得，，．所以．所以．4.如图，有三个正方形的顶点、、恰好在同一条直线上，其中正方形的边长为10厘米，求阴影部分的面积．【答案】100【解析】对于这种几个正方形并排放在一起的图形，一般可以连接正方形同方向的对角线，连得的这些对角线互相都是平行的，从而可以利用面积比例模型进行面积的转化．如右图所示，连接、、，则，根据几何五大模型中的面积比例模型，可得，，所以阴影部分的面积就等于正方形的面积，即为平方厘米．5.如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少？【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．6.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．7.右图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．【答案】49.5【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)．8.如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？【答案】【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米．，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米．9.如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少．【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．10.如图，是梯形的一条对角线，线段与平行，与相交于点．已知三角形的面积比三角形的面积大平方米，并且．求梯形的面积．【答案】28【解析】连接．根据差不变原理可知三角形的面积比三角形大4平方米，而三角形与三角形面积相等，因此也与三角形面积相等，从而三角形的面积比三角形的大4平方米．但，所以三角形的面积是三角形的，从而三角形的面积是(平方米)，梯形的面积为：(平方米)．11.如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，求三角形的面积．【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．12.如图，长方形的面积是36，是的三等分点，，则阴影部分的面积为多少？【答案】2.7【解析】如图，连接．根据蝴蝶定理，，所以；，所以．又，，所以阴影部分面积为：．13.如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．14.已知正方形的边长为10，，，则？【答案】53【解析】如图，作于，于．则四边形分为4个直角三角形和中间的一个长方形，其中的4个直角三角形分别与四边形周围的4个三角形相等，所以它们的面积和相等，而中间的小长方形的面积为，所以．15.如下图，长方形和长方形拼成了长方形，长方形的长是20，宽是12，则它内部阴影部分的面积是多少．【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半，为．16.长方形的面积为36，、、为各边中点，为边上任意一点，问阴影部分面积是多少？【答案】13.5【解析】解法一：寻找可利用的条件，连接、，如下图：可得：、、，而即；而，．所以阴影部分的面积是：解法二：特殊点法．找的特殊点，把点与点重合，那么图形就可变成右图：这样阴影部分的面积就是的面积，根据鸟头定理，则有：．17.在长方形内部有一点，形成等腰的面积为16，等腰的面积占长方形面积的，那么阴影的面积是多少？【答案】3.5【解析】先算出长方形面积，再用其一半减去的面积(长方形面积的)，再减去的面积，即可求出的面积．根据模型可知，所以，又与的面积相等，它们的面积和等于长方形面积的一半，所以的面积等于长方形面积的，所以．18.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分的面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．19.如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．20.如图，长方形的面积是36，是的三等分点，,求阴影部分的面积．【答案】2.7【解析】如图，连接．根据蝴蝶定理，，所以；，所以．又，，所以阴影部分面积为：．。

图形分割组合练习题六年级一、题目描述在六年级数学中，图形分割组合是一个非常重要的知识点。

它既能提高学生解决问题的能力，也能培养学生的观察力和创造力。

为了帮助六年级的学生更好地掌握这个知识点，我们设计了一些图形分割组合练习题。

请同学们根据题目要求进行解答，并在纸上画出图形分割的结果。

二、练习题1. 以下是一个正方形图形，请你将它分割成两个全等的长方形。

2. 已知正方形被分割成了三个相等的小正方形，请你用直线将它们分割成完全相同的图形，每个图形都包含有正方形的一部分。

3. 以下是一个随机组合的图形，请你用直线将它分割成四个全等的图形。

4. 以下是一个正方形图形，请你用直线将它分割成五个全等的图形。

5. 以下是一个矩形图形，请你用直线将它分割成六个全等的图形。

6. 以下是一个随机组合的图形，请你用直线将它分割成七个全等的图形。

7. 以下是一个正方形图形，请你用直线将它分割成八个全等的图形。

8. 以下是一个正方形图形，请你用直线将它分割成九个全等的图形。

9. 以下是一个正方形图形，请你用直线将它分割成十个全等的图形。

10. 以下是一个随机组合的图形，请你用直线将它分割成十一个全等的图形。

三、解答要点1. 第一题中，将正方形分成两个全等的长方形，可以沿着对角线将正方形分割，使得两个长方形完全相等。

2. 第二题中，需要将正方形分成三个全等的图形。

可以将正方形切割成三个全等的大小和形状的三角形，或者通过画一条从正方形的一个顶点到另一个顶点的线，将正方形切割成大小相等的两个梯形和一个平行四边形。

3. 第三题中，需要将图形分割成四个全等的部分。

可以沿着一条对角线将图形分割成大小相等的两个三角形，然后再沿着另一条对角线分割每个三角形，得到四个全等的部分。

4. 第四题中，需要将正方形分割成五个全等的图形。

可以先将正方形分割成四个全等的正方形，然后再通过画一条线将其中一个正方形切割成两个全等的直角三角形。

5. 第五题中，需要将矩形分割成六个全等的图形。

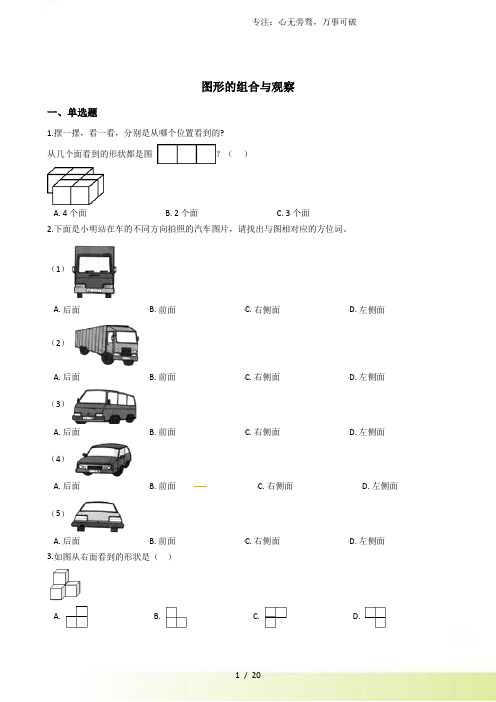
图形的组合与观察一、单选题1.摆一摆，看一看，分别是从哪个位置看到的?从几个面看到的形状都是图？（）A. 4个面B. 2个面C. 3个面2.下面是小明站在车的不同方向拍照的汽车图片，请找出与图相对应的方位词。

（1）A. 后面B. 前面C. 右侧面D. 左侧面（2）A. 后面B. 前面C. 右侧面D. 左侧面（3）A. 后面B. 前面C. 右侧面D. 左侧面（4）A. 后面B. 前面C. 右侧面D. 左侧面（5）A. 后面B. 前面C. 右侧面D. 左侧面3.如图从右面看到的形状是（）A. B. C. D.4.小明准备过马路时，一辆汽车从他的面前驶过，哪幅图是他第一个看到的？（）A. B. C.5.王大伯晚上散步，当他走向路灯时，他的影子会越来越( )A. 小B. 长C. 短6.如果你按照下面的步骤做，当你完成第五步的时候，将纸展开，你会得到（）A. B. C. D.7.看图回答.下面的图形是从上边物体的哪一面看到的？（）.A. 正面B. 侧面C. 上面8.小强用同样大的小正方体摆了一个长方体，从正面和上面看，看到的图形分别是：如图小强摆这个长方体一共用了（）个小正方体．A. 12B. 18C. 249.从上面看到的形状不同的是（）A. B. C.10.用相同的小正方体拼成一个大正方体，至少需要( )个小正方体。

A. 4B. 8C. 16D. 32二、判断题11.这四个图形中只有一个图形不能密铺…．12.若干个完全相同的三角形能密铺．13.由远往近观察某一物体时，距离物体越近，看到的范围越大。

14.把两个一样的正方体拼成一个长方体后，体积和表面积都不变．（判断对错）15.正五边形是轴对称图形，它也能密铺．16.淘气看到的是。

17.从侧面看到的是圆形。

18.人越来越远离窗子时，看到的窗外的范围会越来越窄．19.从上面看小药箱，应该是。

（）20.两个正方体摆成一排，从正面和上面看到的都是长方形。

三、填空题21.把一个棱长是10分米的正方体木料削成一个最大的圆柱体木料，圆柱体木料的体积是________．22.下面的三个图形分别是从哪个方向看到的？填一填。

六年级数学下册组合图形专项练习1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方
形ABCD的1/3，求三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）
部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部
分大6cm2，求S阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）。

组合图形1、求下列组合图形阴影部分的面积。

2、①求它的周长和面积。

（单位：厘米）②圆的周长是18.84cm，求阴影部分面积。

③长方形的面积和圆的面积相等，已知圆④求直角三角形中阴影部分的面积。

的半径是3cm，求阴影部分的周长和面积。

（单位：分米）
⑤下图中长方形长6cm，宽4cm，已知阴影⑥图中阴影①比阴影②面积小48平方厘米，
①比阴影②面积少3cm2，求EC的长。

AB=40cm，求BC的长。

⑦平行四边形的面积是30cm2，⑧一个圆的半径是4cm，求阴影部分面积。

求阴影部分的面积。

⑨已知AB=8cm，AD=12cm，三角形ABE和三角形ADF的面积，各占长方形ABCD的1/3，求
三角形AEF的面积。

⑩梯形上底8cm，下底16cm，阴影⑾求阴影部分面积。

（单位：cm）部分面积64cm2，求梯形面积。

⑿梯形面积是48平方厘米，阴影部分比空白⒀阴影部分比空白部分大6cm2，求S 阴。

部分12平方厘米，求阴影部分面积。

3、求下列图形的体积。

（单位：厘米）
资料整理:小学数学教学网 更多资料请登录小学数学网查看。

组合图形的面积一、单项选择题1.如图中的阴影局部面积是〔〕平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影局部的面积是〔〕平方厘米．〔单位：厘米〕A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°，高等于上底，下底为9，那么梯形的面积为〔〕。

A. 27B. 18C. 36D. 244.图中阴影局部的面积是〔〕平方厘米．A. 24B. 28C. 325.下面三幅图的阴影局部的面积相比较，( )的面积大。

A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影局部的面积为________ (结果保存π)．7.如图中三角形的面积是10平方厘米，图中圆的面积是________平方厘米．8.看图计算〔单位：厘米〕组合图形的面积是________平方厘米9.求以下列图形的面积是________dm2。

〔单位：dm〕10.图中正方形的面积是12平方厘米，圆的面积是________平方厘米．11.计算下面图形阴影局部的面积________．(单位：厘米)12.〔2021•长沙〕如图，两个正方形的边长分别是8厘米和4厘米，那么阴影局部的面积是________平方厘米．13.先求右面图形中涂色局部的面积，再求小正方形的面积．涂色面积________平方分米，小正方形面积________平方分米．14.看图计算〔单位：厘米〕平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.以下列图表示的是一间房子侧面墙的形状．它的面积是________平方米．16.求下面各图阴影局部的面积〔1〕________〔2〕________17.计算下面图形的面积________．(单位：厘米)18.有一条引水渠穿过了一块麦地，这块地的总面积是引水渠占去的面积的________倍？19.把一个长12厘米，宽8厘米的长方形纸片剪下一个最大的正方形，剩下局部的面积是________平方厘米．20.求阴影局部的面积．________平方厘米21.大正方形边长为8厘米，小正方形边长为4厘米，阴影局部的面积是________平方厘米。

六年级组合图形练习题在六年级数学学习中，组合图形是一个重要的概念。

通过组合图形的练习，学生们可以锻炼自己的观察力、想象力和逻辑思维能力。

本文将提供一些六年级组合图形练习题，帮助学生们巩固相关知识，并提升解题能力。

以下是一些题目及其解答。

题目一：请根据下图中的组合图形，回答问题。

（插入图像）1. 这个图形由几个单元图形组成？2. 单元图形的种类以及数量是什么？3. 这些图形的面积之和是多少？解答一：1. 这个图形由六个单元图形组成。

2. 单元图形的种类为正方形和长方形，正方形数量为三个，长方形数量为三个。

3. 这些图形的面积之和为...(根据图形具体计算得出结果)。

题目二：请根据下图中的组合图形，回答问题。

（插入图像）1. 这个图形由几个单元图形组成？2. 单元图形的种类以及数量是什么？3. 这些图形的周长之和是多少？解答二：1. 这个图形由五个单元图形组成。

2. 单元图形的种类为正方形和三角形，正方形数量为三个，三角形数量为两个。

3. 这些图形的周长之和为...(根据图形具体计算得出结果)。

题目三：请根据下图中的组合图形，回答问题。

（插入图像）1. 这个图形由几个单元图形组成？2. 单元图形的种类以及数量是什么？3. 这些图形的总体积是多少？解答三：1. 这个图形由八个单元图形组成。

2. 单元图形的种类为正方体和长方体，正方体数量为三个，长方体数量为五个。

3. 这些图形的总体积为...(根据图形具体计算得出结果)。

通过以上的组合图形练习题，学生们可以提高对组合图形的理解和解题能力。

希望同学们能够认真思考每个问题，并尝试自己独立解答。

如果遇到困难，可以向老师或同学寻求帮助，共同进步。

祝大家在六年级的数学学习中取得好成绩！。

2024年人教版六年级下册数学小升初分班考专题：图形的拼组一、单选题1．下图是一个长3厘米、宽与高都是2厘米的长方体。

将它挖掉一个棱长1厘米的小正方体，它的表面积（ ）。

A．比原来大B．比原来小C．不变D．无法确定2．在一个长、宽、高分别是30厘米、25厘米、60厘米的长方体箱子里，最多能装进棱长1分米的立方体（ ）个。

A．45B．30C．36D．723．城市义工协会开展垃圾分类宣传进社区活动。

他们计划在下面右边这张直角梯形卡纸上剪出如左边那样大小的三角形制作宣传标志（如下图），最多可以剪出（ ）个这样的三角形。

A．3B．4C．5D．64．如图，把一个底面半径4分米、高8分米的圆柱切开并拼成一个近似的长方体。

下面说法中错误的是（ ）A．长方体的体积与圆柱的体积相等B．长方体的底面积等于圆柱的底面积C．长方体的高等于圆柱的高D．长方体的表面积等于圆柱的表面积5．一个长9厘米、宽6厘米、高3厘米的长方体，切割成3个体积相等的长方体，表面积最大可增加（ ）A．36平方厘米B．72平方厘米C．108平方厘米D．216平方厘米6．在一个棱长为1dm的正方体的8个角上，各锯下一个棱长为1cm的正方体，现在它的表面积和原来比（ ）。

A．不变B．减少C．增加D．无法确定二、填空题7．在一块边长是20cm的正方形纸上画一个最大的圆，这个圆的面积是 cm2。

8．用三个完全一样的正方体，拼成一个长方体，长方体的表面积是70平方分米，原来一个正方体的表面积是 平方分米。

9．用3个棱长2分米的正方体拼成一个长方体。

这个长方体的体积是 立方分米，表面积是 平方分米。

10．如图，这个圆的直径是6厘米，把这个圆剪拼成一个近似的长方形，那么这个长方形的宽约 厘米，长方形的长约是 厘米。

11．一个正方体的棱长总和是24厘米，这个正方体的体积是 立方厘米，用两个这样的正方体拼成一个长方体，这个长方体的表面积是 平方厘米．12．如图形体是由棱长为1厘米的小正方体搭拼成的，它的表面积是 平方厘米，至少还需要 个这样的小正方体，才能搭拼成棱长为3厘米的一个正方体.13．一个高5厘米的圆柱体，沿底面直径将圆柱体锯成两块，其表面积增加40平方厘米，原来这个圆柱体的体积是 立方厘米。

组合图形的面积一、单选题1.如图中的阴影部分面积是（）平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影部分的面积是（）平方厘米．（单位：厘米）A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°，高等于上底，下底为9，那么梯形的面积为（）。

A. 27B. 18C. 36D. 244.图中阴影部分的面积是（）平方厘米．A. 24B. 28C. 325.下面三幅图的阴影部分的面积相比较，( )的面积大。

A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影部分的面积为________ (结果保留π)．7.已知如图中三角形的面积是10平方厘米，图中圆的面积是________平方厘米．组合图形的面积是________平方厘米9.求下列图形的面积是________dm2。

（单位：dm）10.图中正方形的面积是12平方厘米，圆的面积是________平方厘米．11.计算下面图形阴影部分的面积________．(单位：厘米)12.（2015•长沙）如图，两个正方形的边长分别是8厘米和4厘米，则阴影部分的面积是________平方厘米．13.先求右面图形中涂色部分的面积，再求小正方形的面积．涂色面积________平方分米，小正方形面积________平方分米．平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.下图表示的是一间房子侧面墙的形状．它的面积是________平方米．16.求下面各图阴影部分的面积（1）________（2）________17.计算下面图形的面积________．(单位：厘米)18.有一条引水渠穿过了一块麦地，这块地的总面积是引水渠占去的面积的________倍？19.把一个长12厘米，宽8厘米的长方形纸片剪下一个最大的正方形，剩下部分的面积是________平方厘米．20.求阴影部分的面积．________平方厘米21.大正方形边长为8厘米，小正方形边长为4厘米，阴影部分的面积是________平方厘米。

2020-2021学年冀教版数学六年级下册期末复习《组合图形的面积》专项训练卷学校:___________姓名：___________班级：___________考号：___________一、选择题1．下图中每个小方格的面积为1cm2，五角星图（阴影部分）的面积约（）1cm2。

A．26~30B．19~25 C．9~18 D．4~82．阴影部分的面积是（）平方厘米．A．52B．30C．22D．无法确定3．两个完全一样的直角三角形重叠成右图形状，形成两个梯形，这两个梯形的面积大小关系是( )。

A．A大B．B大C．相等D．无法确定4．如图，平行四边形ABCD的底BC长是12厘米，线段FE长是4厘米，那么平行四边形中的阴影部分面积是（）平方厘米．A．24B．36C．48D．72二、判断题5．计算组合图形的面积也要用到基本图形的面积公式．（______）6．任何一个梯形都可以分成两个等高的三角形．（____）7．面积相等的图形，形状一定相同．_____三、填空题8．用________原理对组合图形进行分割时，图形的面积大小________。

9．计算下面组合图形的面积________平方厘米10．图中正方形的面积是12平方厘米，圆的面积是________平方厘米．11．如图，长方形的宽是4cm，图中阴影部分面积是________cm2．12．已知三角形ABC的面积为48平方厘米，D、E分别为AB、BC的中点，阴影面积是________平方厘米．四、图形计算13．计算组合图形的面积．(单位：cm)14．有一块土地如图所示，你能求出它的面积？（单位：米）15．求阴影部分的面积．16．求阴影部分的面积（单位，厘米）五、解答题17．计算下面两个图形阴影的面积。

(单位：厘米) （1）（2）18．图中阴影部分的面积一样大吗？为什么？参考答案1．C【解析】【详解】略2．C【分析】由图可知：两个正方形的面积减去空白大三角形的面积就是阴影部分的面积．【详解】6×6+4×4-（6+4）×6÷2，=52﹣30，=22（平方厘米）；答：阴影部分的面积是22平方厘米．故选C．3．C【解析】【详解】略4．C【分析】先求出三角形BFC的面积，因为两个空白三角形的面积相等，所以三角形GBC与三角形CAD 面积相等，都是四边形ABCD面积的一半，而三角形GFC是公共部分，所以三角形FAG与三角形CGD的面积之和与三角形FBC的面积相等，从而可以求出阴影部分的面积.【详解】因为△FAG与△CGD的面积之和与△FBC的面积相等，所以△GBC与△C AD的面积相等，阴影部分的总面积是：12×4÷2×2=48÷2×2=48(平方厘米)故答案为C5．√【分析】在计算组合图形的面积，一般通过分割法或添补的方法，把它转化成基本图形后进行计算【详解】在计算组合图形的面积，把它转化成基本图形后进行计算,所以也要用到基本图形的面积公式。

六年级数学组合图形的面积试题1.图中正六边形ABCDEF的面积是54，AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．【答案】31【解析】如图，将正六边形ABCDEF等分为54个小正三角形．根据平行四边形对角线平分平行四边形面积，面积，面积，四边形ABQP面积．上述三块面积之和为．因此，阴影四边形CEPQ面积为．2.把同一个三角形的三条边分别5等分、7等分(如图1，图2)，然后适当连接这些等分点，便得到了若干个面积相等的小三角形．已知图1中阴影部分面积是294平方分米，那么图2中阴影部分的面积是______平方分米．【答案】200【解析】图1中阴影部分占整个三角形面积的，图2中阴影部分占整个三角形面积的，故图2中阴影部分的面积为294÷=200(平方分米)．3.如图涂阴影部分的小正六角星形面积是16平方厘米，问：大正六角星形面积是多少平方厘米？【答案】48【解析】如图，涂阴影部分的小正六角星形可分成12个与三角形PMN全等(能完全重叠地放在一起)的小三角形．而图中的大正六角星形除去小正六角星形后．有6×4=24个与三角形PMN全等的小三角形，所以大正六角星形的面是小正六角星形的3倍，即48平方厘米．4.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如上中图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．5.如图，在角的两边上分别有、、及、、六个点，并且、、、、的面积都等于1，则的面积等于多少？【答案】【解析】根据题意可知，，所以，．6.如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．7.在边长为6厘米的正方形内任取一点，将正方形的一组对边二等分，另一组对边三等分，分别与点连接,求阴影部分面积．【答案】15【解析】（法1）特殊点法．由于是正方形内部任意一点，可采用特殊点法，假设点与点重合，则阴影部分变为如图所示，图中的两个阴影三角形的面积分别占正方形面积的和，所以阴影部分的面积为平方厘米．（法2）连接、．由于与的面积之和等于正方形面积的一半，所以上、下两个阴影三角形的面积之和等于正方形面积的，同理可知左、右两个阴影三角形的面积之和等于正方形面积的，所以阴影部分的面积为平方厘米．8.如右图所示，在梯形中，、分别是其两腰、的中点，是上的任意一点，已知的面积为，而的面积恰好是梯形面积的，则梯形的面积是（）．【答案】100【解析】如果可以求出与的面积之和与梯形面积的比，那么就可以知道的面积占梯形面积的多少，从而可以求出梯形的面积．如图，连接、．则，，于是．要求与梯形的面积之比，可以把梯形绕点旋转，变成一个平行四边形．如下图所示：从中容易看出的面积为梯形的面积的一半．(也可以根据，，得来)那么，根据题意可知的面积占梯形面积的，所以梯形的面积是．小结：梯形一条腰的两个端点与另一条腰的中点连接而成的三角形，其面积等于梯形面积的一半，这是一个很有用的结论．本题中，如果知道这一结论，直接采用特殊点法，假设与重合，则的面积占梯形面积的一半，那么与合起来占一半．9.如图，ABCD为平行四边形，EF平行AC，如果ADE的面积为4平方厘米．求三角形CDF的面积．【答案】4【解析】连结AF、CE．∴；；又∵AC与EF平行，∴．∴(平方厘米)．10.如图所示，长方形内的阴影部分的面积之和为70，，，四边形的面积为多少?【答案】10【解析】利用图形中的包含关系可以先求出三角形、和四边形的面积之和，以及三角形和的面积之和，进而求出四边形的面积．由于长方形的面积为，所以三角形的面积为，所以三角形和的面积之和为；又三角形、和四边形的面积之和为，所以四边形的面积为．另解：从整体上来看，四边形的面积三角形面积三角形面积白色部分的面积，而三角形面积三角形面积为长方形面积的一半，即60，白色部分的面积等于长方形面积减去阴影部分的面积，即，所以四边形的面积为．。

组合图形的体积尊典题探究例1.棱长是1cm的小立方体组成如图所示的几何体，那么这个几何体的体积是10立方厘米，表面积是36平方厘米.例2.计算体积.（单位：厘米）例3.有一个深4分米的长方体容器，其内侧底面为边长3分米的正方形.当容器底面的一边紧贴桌面倾斜如图时，容器内的水刚好不溢出.容器内的水有22.5升.例4.有一个棱长是10厘米的正方体木块，在它的上、左、前三个面中心分别穿一个3厘米见方的孔，直至对面.求穿孔后木块的体积.演练方阵A档（巩固专练）选择题（共5小题）1.如图，三个半径分别为1米、1.5米和2米的同轴圆柱，每个圆柱高0.5米，这三个圆柱组成一个立体图形，这个立体图形的表面积是（）平方米.卜，］米I2来—iA.42.39B.39.25C.36.11D.25.123.把一个底面直径为a,高为a的圆柱恰好放入正方体盒子里，此时盒子剩余空间（）A-（1-2L）a3B-（1-—）a3C'（1-2L）a3D，（1- —）a3 3412244.两个棱长1分米的正方体并成一个长方体，并成的长方体的表面积（）原两个正方体的表面积之和.A.大于B.小于C.等于5.用两根完全相同的圆柱形木料分别制作成右图中的两个模型（图中涂色部分），甲与乙的体积相比（）C.相等二.填空题（共13小题）6.如图中，每个小长方体的体积都是1立方厘米，那么图形的体积是,表面积是-7.如图，是一个直立于水平面上的几何体（它是圆柱的一部分，下底面为圆面，单位：cm）.则这个几何体的体积为cm3.（计算结果保留兀）8.有一个草堆，上部是一个圆锥，下部是一个圆柱，圆锥高1.5m,底面半径2m,圆柱高3m,底面半径2m,这个草堆的体积是m3.9.（•富源县）如图有个棱长为20cm的正方体木箱堆放在墙角的形状，这些木箱的体积是_____________cm3.10.（•北京）一支未用过的圆柱形铅笔，长18厘米，体积是9立方厘米.使用一段时间后,变成了如图的样子.这时体积是多少立方厘米？11.（•万州区）以直角梯形的上底为轴旋转一周，所得的立体图形的体积是立方厘米.（兀值取整数3）12.如图，计算出它的体积为单位：厘米.A.n(24-2)2x3x(1+1)B./ix22x3x(1+1)33C.n(2+2)2xlx(3+3)D.形(2+2)2x3xlx4.3313.以棱长10厘米的正方体的一个面，挖去一直径为4厘米的圆孔（挖去的圆孔为圆柱体）,则挖去后这个物体的体积是立方厘米.14.如图1,是三个直立于水平面上的形状完全相同的几何体（下底面为圆面.单位：cm）.将它们拼成如图2的新几何体，则该新几何体的体积为cn?.（计算结果保留兀）15.（•崇文区）一个长20厘米、宽10厘米、高20厘米的无盖长方体玻璃容器，里面盛有一些红色溶液.小明想知道溶液的深，他将一根底面边长5厘米，长1米的长方形木条垂直插入到容器底部，取出后量得木条被染红的部分长16厘米.原来容器内红色溶液深_厘米.16.（•大安区）一根长方体木料，横截面是边长10厘米的正方形.从这根木料上截下6厘米长的一段，切削成一个最大的圆锥.圆锥的体积是cn?,约占截下这段长方体木料体积的_____________%（百分号前面保留一位小数）.17.（•武汉模拟）已知某几何体的三视图如图所示，则该几何体的体积为（结果保留71）18.最早将圆周率精确地计算到小数点后面7位，请借助圆周率计算立体图形（如图）的侧面积为平方厘米.6chl4cm2c mB档（提升精练）一.解答题（共9小题）1.（•临川区）有一个粮仓，它们上面是圆锥体，下面是圆柱体，已知圆柱的底面周长是18.84米，高为4米，圆锥的高是1米，则这个粮仓的体积是多少立方米？2.（•汉阳区）如图是丰裕粮仓示意图.如果每立方米稻谷重600千克，这个粮仓可储存稻谷多少千克?3.（•龙泉驿区）请计算零件的表面积和体积（正方体棱长10cm,圆柱的半径r=4cm,高h=6cm）.4.（»±海）如图，（单位：dm）是一块零件的铜铸毛坯，每立方分米铜重8.9千克，这块零件铸铁毛坯的重量是多少吨？5.（•广州模拟）有一根长20厘米，半径为2厘米的圆钢，在它的两端各钻了一个深为4厘米，底面半径为2厘米的圆锥形小孔做成一个零件，如图这个零件的体积是多少立方厘米？6.（•陆良县模拟）每立方厘米的钢重7.8克，求下面一段钢管约重多少千克？（得数保留一位小数）（单位：厘米）（/］。

组合图形的面积练习题
1.如图，△ABC的面积为14平方厘米，DC=3DB，AE=ED．求阴影部分的面积．
2. 如图ADFC是长方形，已知三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米。

求阴影部分的面积。

3. 如图，在三角形ABC中，BD:DC=1:2，E为AD的中点，若三角形ABC的面积为120平方厘米，则阴影部分的面积是多少平方厘米?
4.如图，将边长为6厘米和8厘米的两个正方形并排放在一起，求阴影部分的面积。

5.求图中阴影部分的面积。

（单位：厘米）
6.已知正方形ABCD的边长为8，E为AD中点，P为CE中点，求△BDP的面积。

7.如图，平行四边形ABCD的边长BC为10厘米，直角三角形BCE的直角边EC 为8厘米，已知阴影部分的面积比三角形EFG的面积大4.5平方厘米，则CF的长是多少厘米。

小升初真题特训：组合图形的面积-小学数学六年级下册人教版学校:___________姓名：___________班级：___________考号：___________1A．（1）号面积最大B．（2）号面积最大二、填空题7．（2020·江苏南通·统考小升初真题）如图，大正方形被分成了4个相同的三角形和一个小正方形。

大正a b ，则小正方形的面积是()平方厘米。

方形的周长为24厘米，已知:2:18．（2021·全国·小升初真题）（汉阳区）如图，将两个正三角形重叠作出一个星形，在重叠的图形中再作出一个小星形，即阴影部分，已知大星形的面积是40cm2，那么小星形的面积是_____．9．（2020·北京海淀·小升初真题）如图，已知大正方形的面积是a，则小正方形的面积是___________。

10．（2020·北京海淀的面积的面积＝的面积＝，由此发现，，15．（2020·全国·小升初真题）5平方分米．三、图形计算20．（2022·湖北十堰·统考小升初真题）如图，两个正方形的边长分别是10cm和4cm，求阴影部分的面积。

21．（2022·山东临沂·统考小升初真题）求如图阴影部分的面积。

四、解答题22．（2022·湖南长沙·长沙市开福区青竹湖湘一外国语学校校考小升初真题）如图，大小正方形的边长分别是5厘米、3厘米，求三角形DBF的面积。

23．（2020·江苏常州·校考小升初真题）如下图所示，把三角形DBE沿线段AC折叠，得到一个多边形27．（2021·浙江宁波·小升初真题）28．（2020春·辽宁·六年级统考小升初模拟）如下图，一张边长为4cm的正方形纸，从相邻两边的中点连一条线段，沿这条线段剪去一个角，剩余部分面积是多少？29．（2021春·江苏·六年级统考小升初模拟）如图，一块长方形绿地中有一条弯曲的小路，准备在小路的两侧铺上草坪．草坪的面积是多少平方米？（单位：米）30．（2020·河北·小升初真题）李大爷家承包了如图所示的一块地，请你帮他计算一下这块地的面积（单位，米）。

六年级数学组合图形的面积试题答案及解析1.两个边长相等的正方形各被分成25个大小相同的小方格．现将这两个正方形的一部分重叠起来，若左上角的阴影部分(块状)面积为，右下角的阴影部分(线状)面积为，求大正方形的面积．【答案】19【解析】块状部分与线状部分之间的部分称为D，则D与前者共14个方格，与后者共17个方格，因此每个方格的面积是大正方形的面积为．2.把同一个三角形的三条边分别5等分、7等分(如图1，图2)，然后适当连接这些等分点，便得到了若干个面积相等的小三角形．已知图1中阴影部分面积是294平方分米，那么图2中阴影部分的面积是______平方分米．【答案】200【解析】图1中阴影部分占整个三角形面积的，图2中阴影部分占整个三角形面积的，故图2中阴影部分的面积为294÷=200(平方分米)．3.求下列各个格点多边形的面积．【答案】15,20,14,17【解析】⑴∵；，∴(面积单位)；⑵∵；，∴(面积单位)；⑶∵；，∴(面积单位)；⑷∵；，∴(面积单位)．4.如图，每一个小方格的面积都是1平方厘米，那么用粗线围成的图形的面积是多少平方厘米？【答案】6.5【解析】方法一：正方形格点阵中多边形面积公式：(N+-1)×单位正方形面积，其中N为图形内格点数，L为图形周界上格点数．有N=4，L=7，则用粗线围成图形的面积为：(4+-1)×1=6．5(平方厘米)方法二：如右上图，先求出粗实线外格点内的图形的面积，有①=3÷2=1．5，②=2÷2=1，③=2÷2=1，④=2÷2=1，⑤=2÷2=l，⑥=2÷2=1，还有三个小正方形，所以粗实线外格点内的图形面积为1．5+l+1+1+1+1+3=9．5，而整个格点阵所围成的图形的面积为16，所以粗线围成的图形的面积为：16-9．5=6．5平方厘米．5.四个面积为的正六边形如图摆放，求阴影三角形的面积．【答案】13/6【解析】如图，将原图扩展成一个大正三角形，则与都是正三角形．假设正六边形的边长为为，则与的边长都是，所以大正三角形的边长为，那么它的面积为单位小正三角形面积的49倍．而一个正六边形是由6个单位小正三角形组成的，所以一个单位小正三角形的面积为，三角形的面积为．由于，，所以与三角形的面积之比为．同理可知、与三角形的面积之比都为，所以的面积占三角形面积的，所以的面积的面积为．6.如图，与均为正方形，三角形的面积为6平方厘米，图中阴影部分的面积为多少？【答案】6【解析】如图，连接，比较与，由于，，即与的底与高分别相等，所以与的面积相等，那么阴影部分面积与的面积相等，为6平方厘米．7.如右图，过平行四边形内的一点作边的平行线、，若的面积为8平方分米，求平行四边形的面积比平行四边形的面积大多少平方分米？【答案】16【解析】根据差不变原理，要求平行四边形的面积与平行四边形的面积差，相当于求平行四边形的面积与平行四边形的面积差．如右上图，连接、．由于，所以．而，，所以(平方分米)．8.右图中，和是两个正方形，和相交于，已知等于的三分之一，三角形的面积等于6平方厘米，求五边形的面积．【答案】49.5【解析】连接、，由于与平行，可知四边形构成一个梯形．由于面积为6平方厘米，且等于的三分之一，所以等于的，根据梯形蝴蝶定理或相似三角形性质，可知的面积为12平方厘米，的面积为6平方厘米，的面积为3平方厘米．那么正方形的面积为平方厘米，所以其边长为6厘米．又的面积为平方厘米，所以(厘米)，即正方形的边长为3厘米．那么，五边形的面积为：(平方厘米)．9.正方形ABCD和正方形CEFG，且正方形ABCD边长为10厘米，则图中阴影面积为多少平方厘米？【答案】50【解析】方法一：三角形BEF的面积，梯形EFDC的面积三角形BEF的面积，而四边形CEFH是它们的公共部分，所以，三角形DHF的面积三角形BCH的面积，进而可得，阴影面积三角形BDF的面积三角形BCD 的面积(平方厘米)．方法二：连接CF，那么CF平行BD ，所以，阴影面积三角形BDF的面积三角形BCD的面积(平方厘米)．10.如右图所示，在长方形内画出一些直线，已知边上有三块面积分别是，，．那么图中阴影部分的面积是多少？【答案】97【解析】三角形的面积三角形的面积长方形面积阴影部分面积；又因为三角形的面积三角形的面积长方形面积，所以可得：阴影部分面积．11.如图，长方形的面积是2平方厘米，，是的中点．阴影部分的面积是多少平方厘米？【答案】平方厘米【解析】如下图，连接，、的面积相等，设为平方厘米;、的面积相等，设为平方厘米，那么的面积为平方厘米．，．所以有．比较②、①式，②式左边比①式左边多，②式右边比①式右边大0.5，有，即,．而阴影部分面积为平方厘米．12.如图，已知，，，，线段将图形分成两部分，左边部分面积是38，右边部分面积是65，求三角形的面积．【答案】40【解析】连接，．根据题意可知，；；所以，，，，，于是：；；可得．故三角形的面积是40．13.如图，如果长方形的面积是平方厘米，那么四边形的面积是多少平方厘米？【答案】32.5【解析】如图，过、、、分别作长方形的各边的平行线．易知交成中间的阴影正方形的边长为厘米，面积等于平方厘米．设、、、的面积之和为，四边形的面积等于，则，解得(平方厘米)．14.如图，已知是梯形，∥，，，，求的面积．【答案】6【解析】本题是09年六年级试题，初看之下，是梯形这个条件似乎可以用到梯形蝴蝶定理，四边形内似乎也可以用到蝴蝶定理，然而经过试验可以发现这几个模型在这里都用不上，因为、这两个点的位置不明确．再看题目中的条件，，，这两个条件中的前一个可以根据差不变原理转化成与的面积差，则是与的面积差，两者都涉及到、以及有同一条底边的两个三角形，于是想到过、分别作梯形底边的平行线．如右图，分别过、作梯形底边的平行线，假设这两条直线之间的距离为．再过作的垂线．由于，所以，故．根据差不变原理，这个差等于与的面积之差．而与有一条公共的底边，两个三角形边上的高相差为，所以它们的面积差为，故．再看，它的面积等于是与的面积之差，这两个三角形也有一条公共的底边，边上的高也相差，所以这两个三角形的面积之差为，故．由于，所以，则，所以．15.长方形的面积为36，、、为各边中点，为边上任意一点，问阴影部分面积是多少？【答案】13.5【解析】解法一：寻找可利用的条件，连接、，如下图：可得：、、，而即；而，．所以阴影部分的面积是：解法二：特殊点法．找的特殊点，把点与点重合，那么图形就可变成右图：这样阴影部分的面积就是的面积，根据鸟头定理，则有：．16.一个长方形分成4个不同的三角形，绿色三角形面积占长方形面积的，黄色三角形面积是．问：长方形的面积是多少平方厘米？【答案】60【解析】黄色三角形与绿色三角形的底相等都等于长方形的长，高相加为长方形的宽，所以黄色三角形与绿色三角形的面积和为长方形面积的，而绿色三角形面积占长方形面积的，所以黄色三角形面积占长方形面积的．已知黄色三角形面积是，所以长方形面积等于（）．17.如右图，过平行四边形内的一点作边的平行线、，若的面积为8平方分米，求平行四边形的面积比平行四边形的面积大多少平方分米？【答案】16【解析】根据差不变原理，要求平行四边形的面积与平行四边形的面积差，相当于求平行四边形的面积与平行四边形的面积差．如右上图，连接、．由于，所以．而，，所以(平方分米)．18.如右图，正方形的面积是，正三角形的面积是，求阴影的面积．【答案】2【解析】连接交于点，并连接．如右上图所示，可得，所以与面积相等(同底等高)，所以有:，因为，所以．19.如图所示，正方形的边长为厘米，长方形的长为厘米，那么长方形的宽为几厘米？【答案】6.4【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)．三角形面积等于与它等底等高的平行四边形面积的一半．证明：连接．(我们通过把这两个长方形和正方形联系在一起)．∵在正方形中，边上的高，∴(三角形面积等于与它等底等高的平行四边形面积的一半)同理，．∴正方形与长方形面积相等．长方形的宽(厘米)．20.如右图，在平行四边形中，直线交于，交延长线于，若，求的面积．【答案】1【解析】本题主要是让学生并会运用等底等高的两个三角形面积相等(或夹在一组平行线之间的三角形面积相等)和等量代换的思想．连接．∵∥，∴同理∥，∴又，，∴，即．。